Patrick F. Dunn, Measurement, Data Analysis, and Sensor Fundamentals for Engineering and Science, 2nd Edition

Подождите немного. Документ загружается.

246 Measurement and Data Analysis for Engineering and Science

This region remains attached to an airfoil upon decreasing its angle of

attack from the region of stall.

2. Linearity:

˜e



L,max

F SO





|y − y

max

F SO



. (7.29)

Linearity error is a measure of how linear is the best ﬁt of the instru-

ment’s calibration data. It is deﬁned in terms of its maximum deviation

distance, |y − y

max

3. Sensitivity:

˜e



K,max

F SO





|y − y

nom

max

F SO



. (7.30)

Sensitivity error is characterized by the greatest change in the slope

(static sensitivity) of the calibration ﬁt.

4. Zero-shift:

˜e



Z,max

F SO





shift

− y

nom

max

F SO



. (7.31)

Zero-shift error refers to the greatest possible shift that can occur in the

intercept of the calibration ﬁt.

5. Repeatability:

˜e



F SO



. (7.32)

Repeatability error is related to the precision of the calibration. This is

determined by repeating the calibration many times for the same input

values. The quantity 2S

represents the precision interval of the data

for a particular value of x.

6. Stability:

˜e



S,max

· ∆t

F SO



. (7.33)

Stability error is related to e

S,max

, which is the greatest deviation in the

output value for a ﬁxed input value that could occur during operation.

This deviation is expressed in units of F SO/∆t, with ∆t denoting the

time since instrument purchase or calibration. Stability error is a mea-

sure of how much the output can drift over a period of time for the same

input.

7. Thermal-drift:

˜e



T,max

F SO



. (7.34)

Thermal-drift error is characterized by the greatest deviation in the

output value for a ﬁxed input value, e

T,max

, that could occur during

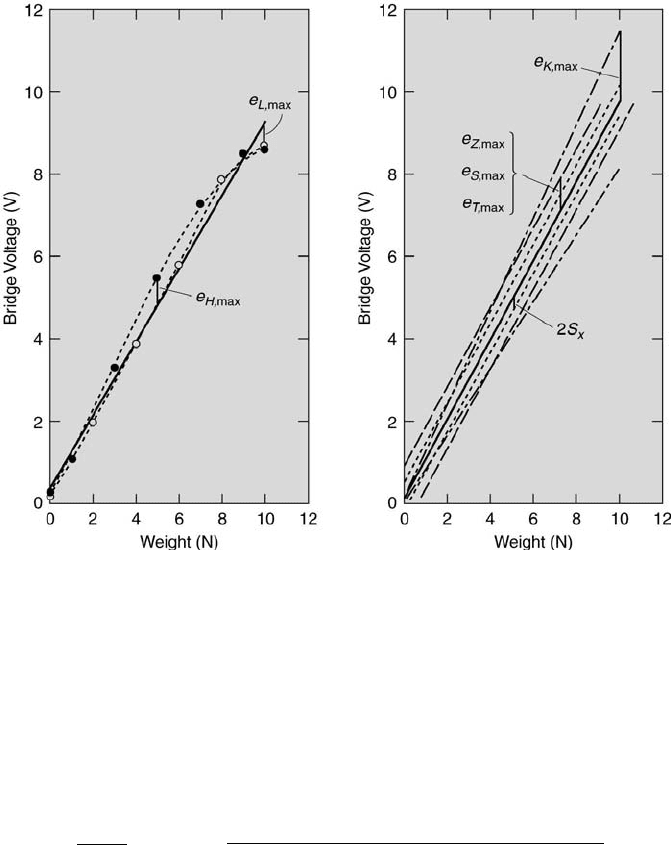
Uncertainty Analysis 247

FIGURE 7.3

Elemental errors ascertained by calibration.

operation because of variations in the environmental temperature. Sta-

bility and thermal-drift errors are similar in behavior to the zero-shift

error.

The instrument uncertainty, u

, combines all the known instrument er-

rors,

= F SO·

˜e

+ ˜e

other

, (7.35)

where ˜e

other

denotes any other instrument errors. All ˜e

’s expressed in Equa-

tion 7.35 are dimensionless.

How are these elemental errors actually assessed? Typically, hysteresis

and linearity errors are determined by performing a single up-scale, down-

scale calibration. The results of this type of calibration are displayed in the

left graph of Figure 7.3. In that graph, the up-scale results are plotted as

open circles and the down-scale results as solid circles. The dotted lines are

linear interpolations between the data. Hysteresis is evident in this example

248 Measurement and Data Analysis for Engineering and Science

by down-scale output values that are higher than their up-scale counterparts.

The best-ﬁt curve of the data is indicated by a solid line. Both the hysteresis

and linearity errors are assessed with respect to the best-ﬁt curve.

Sensitivity, repeatability, zero-shift, stability, and thermal-drift errors

are ascertained by performing a series of calibrations and then determining

each particular error by comparisons between the calibrations. The results

of a series of calibrations are shown in the right graph of Figure 7.3. The

solid curve represents the best-ﬁt of the data from all the calibrations. The

dotted curves indicate the limits within which a calibration is repeatable

with 95 % conﬁdence. The repeatability error is determined from the diﬀer-

ence between either dotted curve and the best-ﬁt curve. The dash-dot curves

identify the calibration curves that have the maximum and minimum slopes.

The sensitivity error is assessed in terms of the greatest diﬀerence between

minimum or maximum sensitivity curve and the best-ﬁt curve. The dashed

curves denote shifts that can occur in the calibration because of zero-shift,

stability, and thermal-drift errors. Each error can have a diﬀerent value and

is determined from the calibration curve having the greatest diﬀerence with

calibration data that occurs with each eﬀect, with respect to the best-ﬁt

curve.

The following two examples illustrate the eﬀects of instrument errors on

measurement uncertainty.

Example Problem 7.5

Statement: A pressure transducer is connected to a digital panel meter. The panel

meter converts the pressure transducer’s output in volts back to pressure in psi. The

manufacturer provides the following information about the panel meter:

Resolution: 0.1 psi

Repeatability: 0.1 psi

Linearity: within 0.1 % of reading

Drift: less than 0.1 psi/6 months within the 32

◦

F to 90

◦

F range

The only information given about the pressure transducer is that it has “an accuracy

of within 0.5 % of its reading”.

Estimate the combined standard uncertainty in a measured pressure at a nominal

value of 100 psi at 70

◦

F. Assume that the transducer’s response is linear with an

output of 1 V for every psi of input.

Solution: The uncertainty in the measured pressure, (u

)

, is the combination of

the uncertainties of the transducer, (u

)

, and the panel meter, (u

)

. This can be

expressed as

)

[(u

)

]

+ [(u

)

]

For the transducer,

)

+ u

= u

= 0.005 × 100 psi = 0.50 psi.

For the panel meter,

)

+ u

Uncertainty Analysis 249

Now,

= 0.5 resolution = 0.05 psi,

(7.36)

+ e

where

(repeatability) = 0.1 psi

(linearity) = 0.1 % reading = 0.001 × 100V/(1V/psi) = 0.1 psi, and

(drift) = 0.1 psi/6 months × 6 months = 0.1 psi,

which implies that

= 0.17 psi,

)

= 0.18 psi,

)

0.50

+ 0.18

= 0.53 psi.

Note that most of the combined standard uncertainty comes from the transducer. So,

to improve the accuracy of the measurement system, a more accurate transducer is

required.

Example Problem 7.6

Statement: An analog-to-digital (A/D) converter with the speciﬁcations listed be-

low (see Chapter 3 for terminology) is to be used in an environment in which the A/D

converter’s temperature may change by ±10

◦

C. Estimate the contributions of con-

version and quantization errors to the combined standard uncertainty in the digital

representation of an analog voltage by the converter.

F SR

0 V to 10 V

M 12 bits

Linearity ±3 bits/E

F SR

Temperature drift 1 bit/5

◦

Solution: The instrument uncertainty is the combination of uncertainty due to

quantization errors, e

, and to conversion errors, e

)

+ e

The resolution of a 12-bit A/D converter with a full scale range of 0 V to 10 V is given

by (see Chapter 2)

Q =

F SR

4096

= 2.4 mV/bit.

The quantization error per bit is found to be

= 0.5Q = 1.2 mV.

The conversion error is aﬀected by two elements:

250 Measurement and Data Analysis for Engineering and Science

linearity error = e

= 3 bits× 2.4 mV/bit

= 7.2 mV.

temperature error = e

1bit

◦

× 10

◦

C × 2.4 mV/bit

= 4.8 mV.

Thus, an estimate of the conversion error is

+ e

(7.2 mV)

+ (4.8 mV)

= 8.6 mV.

The combined standard uncertainty in the digital representation of the analog value

due to the quantization and conversion errors becomes

)

(1.2 mV)

+ (8.6 mV)

= 8.7 mV.

Here the conversion errors dominate the uncertainty. So, a higher resolution converter

is not necessary to reduce the uncertainty. A converter having smaller instrument errors

is required.

These two examples illustrate the process of design-stage uncertainty es-

timation. Once the components of the measurement system have been cho-

sen, uncertainty analysis can be extended to consider other types of errors

that can eﬀect the measurement, such as temporal variations in the system’s

output under ﬁxed conditions. This involves multiple measurements, which

are covered in Section 7.10.

7.9.2 Single-Measurement Result Experiment

The previous section considered estimating the uncertainties of a measurand.

But what about the uncertainty in a result? This uncertainty was introduced

beforehand and is given by Equation 7.21. From this equation, uncertainty

expressions can be developed for speciﬁc analytical relations [4]:

1. If r = Bx, where B is a constant, then

= |B|u

. (7.37)

If r is directly proportional to a measurand through a constant of pro-

portionality B, then the uncertainty in r is the product of the absolute

value of the proportionality constant and the measurand uncertainty.

Uncertainty Analysis 251

2. If r = x + ... + z − (u + ... + w), then

)

+ ... + (u

)

+ (u

)

+ ... + (u

)

. (7.38)

If r is related directly to all of the measurands, then the uncertainty in

r is the combination in quadrature of the measurands’ uncertainties.

3. If r = (x...z)/(u...w), then

|r|





+ ... +









+ ... +





. (7.39)

The quantity u

/|r| is the fractional uncertainty of a result. If r

is related directly and/or inversely to all of the measurands, then the

fractional uncertainty in r is the combination in quadrature of the mea-

surands’ fractional uncertainties.

4. If r = x

, then

|r|

= |n|

|x|

. (7.40)

This equation follows directly from Equation 7.39.

Estimation of the uncertainty in a result is shown in the following ex-

ample.

Example Problem 7.7

Statement: The coeﬃcient of restitution, e, of a ball can be determined by dropping

the ball from a known height, h

, onto a surface and then measuring its return height,

(as described in Chapter 11). For this experiment e =

. If the uncertainty

in the height measurement, u

, is 1 mm, h

= 1.000 m and h

= 0.800 m, determine

the combined standard uncertainty in e.

Solution: Direct application of Equation 7.21 yields



∂e

∂h





∂e

∂h



Now,



∂e

∂h



1/h

√

and



∂e

∂h



−h

√

. Substitution of the known values

into the above equation gives u

(5.59 × 10

−4

)

+ (4.47 × 10

−4

)

= 7.16 ×10

−4

0.0007.

Often there are experiments involving results that have angular depen-

dencies. The values of these results can vary signiﬁcantly with angle because

of the presence of trigonometric functions in the denominators of their un-

certainty expressions. The following two problems illustrate this point.

Example Problem 7.8

Statement: A radar gun determines the speed of a directly oncoming automobile

within 4 %. However, if the gun is used oﬀ angle, another uncertainty arises. Determine

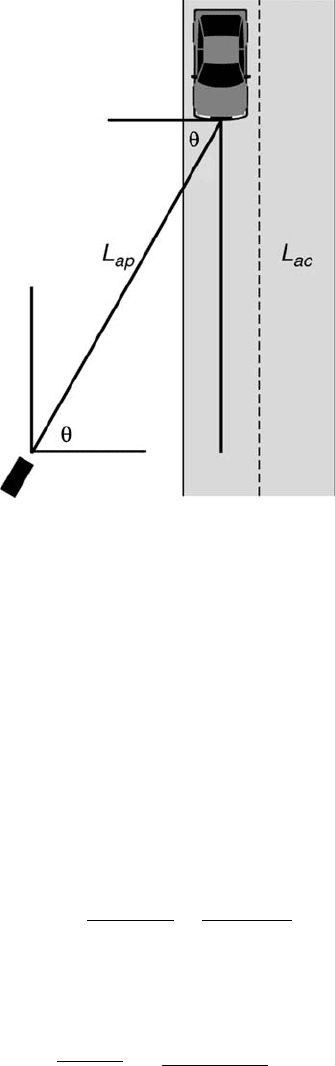
252 Measurement and Data Analysis for Engineering and Science

FIGURE 7.4

Radar detection of a car’s speed.

the gun’s oﬀ-angle uncertainty, u

, as a function of the angle at which the car is viewed.

What is the combined uncertainty in the speed if the oﬀ-angle, θ

, equals 70

◦

? Finally,

what is the overall uncertainty in the speed assuming 95 % conﬁdence?

Solution: A schematic of this problem is shown in Figure 7.4. Assume that the

gun acquires a reading within a very short time period, ∆t. The actual speed, s

, is

the ratio of the actual highway distance travelled, L

, during the time period to ∆t.

Similarly, the apparent speed, s

, equals L

/∆t. From trigonometry,

= L

× sin(θ). (7.41)

Substitution of the speed deﬁnitions into this equation yields

= s

sin(θ). (7.42)

The oﬀ-angle uncertainty can be deﬁned as

| s

− s

| sin(θ) − 1 |

sin(θ)

. (7.43)

Note that when θ = 90

◦

, sin(90

◦

) = 1, which yields u

= 0. This is when the radar

gun is pointed directly along the highway at the car. When θ = 70

◦

, sin(70

◦

) = 0.940,

which yields u

= (| 0.940 − 1 |)/0.940 = 0.064 or 6.4 %. This uncertainty must be

combined in quadrature with radar gun’s instrument uncertainty, u

= 0.04, to yield

the combined uncertainty, u

+ u

0.04

+ 0.064

= 0.075. (7.44)

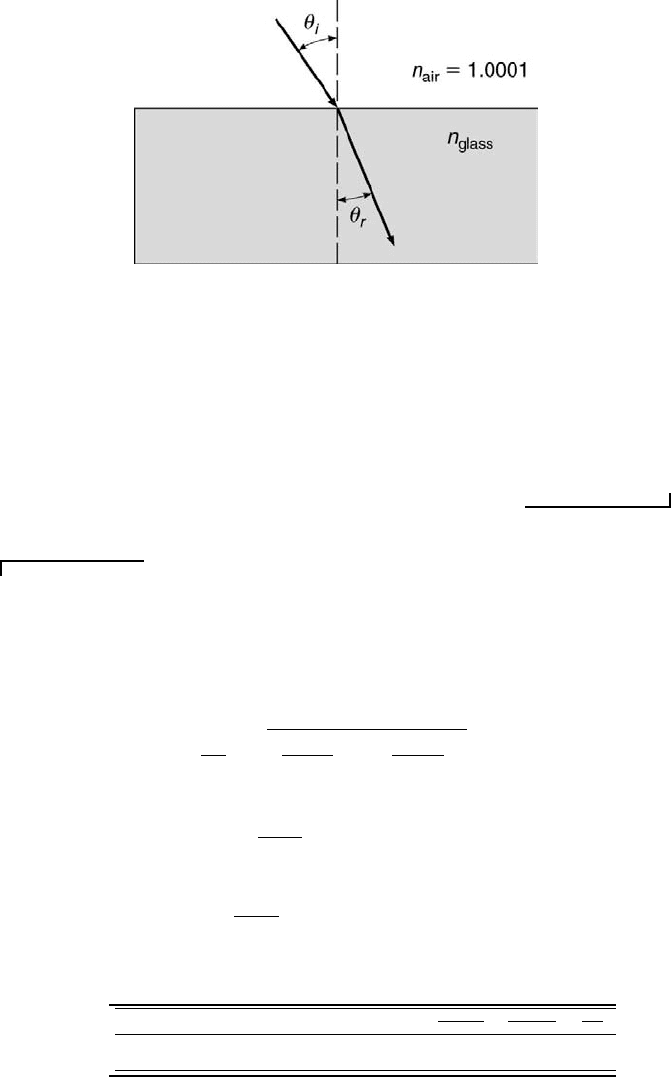
Uncertainty Analysis 253

FIGURE 7.5

A light refraction experiment based on Snell’s law.

So, the combined uncertainty is 7.5 % or almost twice the instrument uncertainty. This

uncertainty increases as the oﬀ-angle increases. Assuming 95 % conﬁdence, the overall

uncertainty is approximately twice the combined uncertainty or 15 %. Thus, assuming

that the indicated speed is 70 mph, the actual speed could be as low as approximately

60 mph (70 − 0.15 × 70) or as high as approximately 80 mph (70 + 0.15 × 70).

Example Problem 7.9

Statement: This problem is adapted from one in [4]. An experiment is constructed

(see Figure 7.5) to determine the index of refraction of an unknown transparent glass.

Find the fractional uncertainty, ∆n/n, in the index of refraction, n, as determined

using Snell’s law, where n = sin θ

/ sin θ

. Assume that the measurements of the angles

are uncertain by ±1

◦

or 0.02 rad.

Solution: It follows that

∆n



∂ sin θ

sin θ





∂ sin θ

sin θ



Now,

∂ sin θ =



d sin θ

dθ



∂θ = |cos θ|∂θ (in rad).

So,

∂ sin θ

|sin θ|

= |cot θ|∂θ (in rad).

These considerations yield the following uncertainties:

± 1

◦

± 1

◦

sin θ

∂ sin θ

| sin θ

∂ sin θ

| sin θ

∆n

20 13.0 0.342 0.225 1.52 5 % 8 % 9 %

40 23.5 0.643 0.399 1.61 2 % 4 % 5 %

254 Measurement and Data Analysis for Engineering and Science

Note that the percentage uncertainty in n decreases with increasing the angle of inci-

dence. In fact, as the angle of incidence approaches that of normal incidence (θ

= 0

◦

the uncertainty tends to inﬁnity.

Many times, experimental uncertainty analysis involves a series of uncer-

tainty calculations that lead to the uncertainty of a desired result. In that

situation, usually it is best to perform the analysis in steps, identifying the

uncertainties in intermediate results. This not only helps to avoid mistakes

made in calculations but also aids in identifying the variables that contribute

signiﬁcantly to the desired result’s uncertainty. The following two examples

illustrate this point.

Example Problem 7.10

Statement: Determine the combined standard uncertainty in the density of air,

assuming ρ = P/RT . Assume negligible uncertainty in R (R

air

= 287.04 J/kg·K). Let

T = 24

◦

C = 297 K and P = 760 mm Hg.

Solution: The uncertainty in the density of air (a result) becomes



∂ρ

∂T





∂ρ

∂P





−P







where

(1 mm Hg) =



1.01 × 10

760 mm Hg

× 1 mm Hg



(133 Pa) = 67 Pa,

and

= 0.5(1

◦

C) = 0.5(1 K) = 0.5 K.

Thus,



101325

(287.04)(297)

(0.5)





(287.04)(297)

(67)



= [4.00 × 10

−6

+ 0.62 × 10

−6

]

= 2.15 × 10

−3

kg/m

Finally,

ρ =

101325

(287.04)(297)

= 1.19 kg/m

⇒

2.15 × 10

−3

1.19

= 0.19 %.

This is a typical value for the combined standard uncertainty in the density as de-

termined from pressure and temperature measurements in a contemporary laboratory.

Uncertainty Analysis 255

Example Problem 7.11

Statement: Consider an experiment in which the static pressure distribution around

the circumference of a cylinder in a cross ﬂow in a wind tunnel is measured. Determine

the combined standard uncertainty in the pressure coeﬃcient, C

, as deﬁned by the

equation

≡

P − P

∞

ρV

∞

. (7.45)

Assume that the pressure diﬀerence P − P

∞

is measured as ∆p using an inclined

manometer with

∆p

= 0.06 in. H

O = 15 N/m

(∆P = 996 N/m

= 2.15 × 10

−3

kg/m

(ρ = 1.19 kg/m

), and

∞

= 0.31 m/s (V

∞

= 40.9 m/s).

Solution: Now, as is clear from Equation 7.45, the pressure coeﬃcient is a result

and is a function of the density, the change in pressure, and the freestream velocity. In

short,

= f (∆p, ρ, V

∞

Therefore, applying Equation 7.21 yields

⇒ u

= [(

∂C

∂∆p

∆p

)

+ (

∂C

∂ρ

)

+ (

∂C

∂V

∞

)

]

= [(

ρV

∞

∆p

)

+ (−

2∆p

∞

)

+ (−

4∆p

ρV

∞

)

]

= [(

(2)(15)

(1.19)(40.9)

)

+ (

(2)(996)(2.15 × 10

−3

)

(1.19)

)(40.9)

)

+ (

(4)(996)(0.31)

(1.19)(40.9)

)

]

= [2.27 × 10

−4

+ 3.27 × 10

−6

+ 2.30 × 10

−4

]

= 0.021.

Alternatively, C

as the ratio of two transducer diﬀerential pressures,

≡

P − P

∞

ρV

∞

∆P

p−s

(∆p = 996 N/m

). (7.46)

Now, assume that u

∆p

= u

∆p

p−s

= 15 N/m

The equation for the uncertainty in C

when Equation 7.46 is used becomes

= [(

∂C

∂∆P

cyl

∆P

cyl

)

+ (

∂C

∂∆P

p−s

∆P

p−s

)

]

= [(

∆P

p−s

∆P

)

+ (−

∆P

cyl

∆P

p−s

∆P

p−s

)

]

= [2(

996

)

]

= 0.021.

The latter measurement approach is easier to determine C

than the former. When

designing an experimental procedure in which the pressure coeﬃcient needs to be de-

termined, it is preferable to ratio the two transducer diﬀerential pressures.