Patrick F. Dunn, Measurement, Data Analysis, and Sensor Fundamentals for Engineering and Science, 2nd Edition

Подождите немного. Документ загружается.

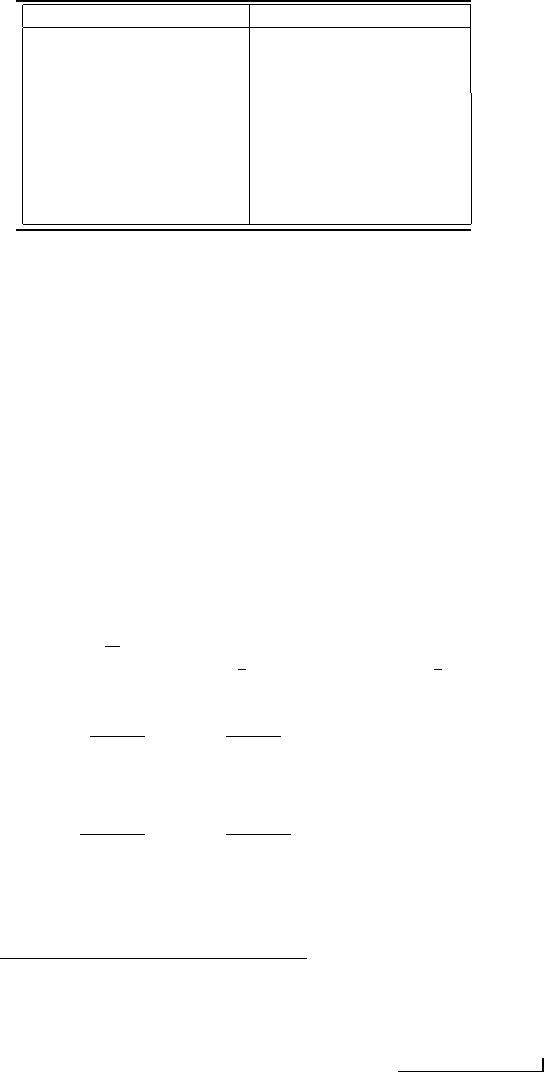
266 Measurement and Data Analysis for Engineering and Science

Applied Weight, W (N)

Output Voltage, E (V)

1.0

3.0

5.0

7.0

9.1

8.9

9.1

9.0

TABLE 7.1

Force-measurement system calibration data.

of the measurement ﬁve times at 5 N of applied weight. The results are presented in

Table 7.1. Determine (a) the static sensitivity of the calibration curve at 3.5 N, (b)

the random uncertainty with 95 % conﬁdence in the value of the output voltage based

upon the data obtained for the 5 N application cases, (c) the range within which the

true mean of the voltage is for the 5 N application cases at 90 % conﬁdence, (d) the

range within which the true variance of the voltage is for the 5 N application cases at

90 % conﬁdence, (e) the standard error of the ﬁt based upon all of the data, and (f)

the design-stage uncertainty of the instrument at 95 % conﬁdence assuming that 0.04

V instrument uncertainty was obtained through calibration.

Solution: The average value of the output voltage for the ﬁve values of the 5 N

case is 9.0 V. Thus, the data can be ﬁtted the best by the line E = 2W + 1. (a)

The sensitivity of a linear ﬁt is the slope, 2 V/N, which is the same for all applied-

weight values. (b) The random uncertainty for the 5 N cases with 95 % uncertainty

is P

= t

ν,P =95 %

P,5N

. Here, S

P,5N

= 0.1 V and ν = 4 with t

4,95

= 2.770. This

implies P

= 0.277 V. (c) The range within which the true mean value is contained

extends ±t

ν,P =90 %

P,5N

√

N = 5 from the sample mean value of 9 V. Here, t

4,90

2.132. So the range is from 9 − (2.132)(0.1)/

√

5 V to 9 + (2.132)(0.1)/

√

5 V, or from

8.905 V to 9.095 V. (d) The range of the true variance is

νS

P,5N

α/2

≤ σ

≤

νS

P,5N

1−α/2

P = 0.90, which implies α = 0.10. So, χ

α/2

for ν = 4 equals 9.49 and χ

1−α/2

equals

0.711. Substitution of these values yields

(4)(0.01)

9.49

≤ σ

≤

(4)(0.01)

0.711

4.22 × 10

−3

≤ σ

≤ 56.26 × 10

−3

This also gives 0.065 V ≤ σ

≤ 0.237 V. (e) The ﬁrst four and one of the ﬁve 5 N

applied-weight case values are on the best-ﬁt line. Therefore, only four of the ﬁve 5 N

case values contribute to the standard error of the ﬁt. Thus

(0.1)

+ (0.1)

+ (−0.1)

+ (0.1)

/(9 − 2) = 0.0756 = 0.1 V.

(f) The resolution of the voltage equals 0.1 V from inspection of the data. This implies

that u

= 0.05 V. This uncertainty is combined in quadrature with the instrument

uncertainty of 0.04 V to yield a design-stage uncertainty equal to 0.064 = 0.06 V.

Uncertainty Analysis 267

7.12 *Finite-Diﬀerence Uncertainties

There are additional uncertainties that need to be considered. These occur

when experiments are conducted to determine a result that depends upon

the integral or derivative of measurand values obtained at discrete loca-

tions or times. The actual derivative or integral only can be estimated from

this discrete information. A discretization (truncation) error results. For ex-

ample, consider an experiment in which the velocity of a moving object is

determined from measurements of time as the object passes known spatial

locations. The actual velocity may vary nonlinearly between the two loca-

tions, but it can only be approximated using the ﬁnite information available.

Similarly, an actual velocity gradient in a ﬂow only can be estimated from

measured velocities at two adjacent spatial locations. Examples involving

integral approximations are the lift and drag of an object, determined from

a ﬁnite number of pressure measurements along the surface of the object,

and the ﬂow rate of a ﬂuid through a duct, determined from a ﬁnite number

of velocity measurements over a cross-section of the duct.

The discretization errors of integrals and derivatives can be estimated,

as described in the following section. Numerical round-oﬀ errors also can

occur in such determinations. For most experimental situations, however,

discretization errors far exceed numerical round-oﬀ errors. When measure-

ments are relatively few, the discretization error can be comparable to the

measurement uncertainty. There are many excellent references that cover

ﬁnite-diﬀerence approximation methods and their errors ([3], [22], [11], and

[24]).

7.12.1 *Derivative Approximation

If the values of a measurand are known at several locations or times, its

actual derivative can be approximated. This is accomplished by representing

the actual derivative in terms of a ﬁnite-diﬀerence approximation based

upon, most commonly, a Taylor series expansion. The amount of error is

determined by the order of the expansion method used.

Suppose f(x) is a continuous function with all of its derivatives deﬁned

at x. The next, or forward, value of f(x + ∆x) can be estimated using a

Taylor series expansion of f(x + ∆x) about the point x. That is,

f(x + ∆x) = f (x) + ∆xf

(x) +

(∆x)

(x) +

(∆x)

000

(x) + . . . . (7.69)

Equation 7.69 can be rearranged to solve for the derivative

(x) =

f(x + ∆x) − f (x)

∆x

−

(∆x)

(x) −

(∆x)

000

(x) + . . . . (7.70)

268 Measurement and Data Analysis for Engineering and Science

The ﬁrst term on the right side is the ﬁnite-diﬀerence representation of

(x) and the subsequent terms deﬁne the discretization error. A ﬁnite-

diﬀerence representation is termed n-th order when the leading term in the

discretization error is proportional to (∆x)

. Thus, Equation 7.70 is known

as the ﬁrst-order, forward-diﬀerence expression for f

(x). If the actual f(x)

can be expressed as a polynomial of the ﬁrst degree, then f

(x) = 0, the

ﬁnite-diﬀerence representation of f

(x) exactly equals the actual derivative

and there is no discretization error. In general, an n-th order method is

exact for polynomials of degree n.

Example Problem 7.18

Statement: The velocity proﬁle of a ﬂuid ﬂowing between two parallel plates spaced

a distance 2h apart is given by the expression u(y) = u

[1 − (y/h)

], where y is the

coordinate perpendicular to the plates. Determine the exact value of u(0.2h)/u

and

compare it with the ﬁnite-diﬀerence values obtained from the Taylor series expansion

that result as each term is included additionally in the series.

Solution: The exact value is found from direct substitution of y = 0.2h into the

velocity proﬁle is u(0.2h)/u

exact

= 0.96. For the Taylor series given by Equation 7.69,

the derivatives must be computed. The result is u

(y) = −2u

y/h

, u

(y) = −2u

and u

000

(y) = 0. Noting that 0.2h = ∆x for this case, substitutions into Equation 7.69

yield u(0.2h)/u

series

= 1 − 0.08 + 0.04 + 0 + . . .. So, three terms are required in the

series in this case to give the exact result; fewer terms result in a diﬀerence between

the exact and series values.

Similarly, the ﬁrst-order, backward-diﬀerence expression for f

(x) is

(x) =

f(x) − f(x − ∆x)

∆x

(∆x)

(x) −

(∆x)

000

(x) + . . . . (7.71)

Equation 7.70 can be added to Equation 7.71 to yield

(x) =

f(x + ∆x) − f (x − ∆x)

2∆x

−

(∆x)

000

(x) + . . . , (7.72)

resulting in a second-order, central-diﬀerence expression for f

(x). Other

expressions for second-order, central-diﬀerence, and central-mixed-diﬀerence

second and higher derivatives can be obtained following a similar approach

[22].

Usually second-order accuracy is suﬃcient for experimental analysis. As-

suming this, the discretization error, e

, of the ﬁrst derivative approximated

by a second-order central-diﬀerence estimate using values at two locations

(x − ∆x and x + ∆x) is

' f

000

(x)

(∆x)

, (7.73)

where f

000

(x) is evaluated somewhere in the interval, usually at its maximum

value. A problem arises, however, because the value of f

000

(x) is not known.

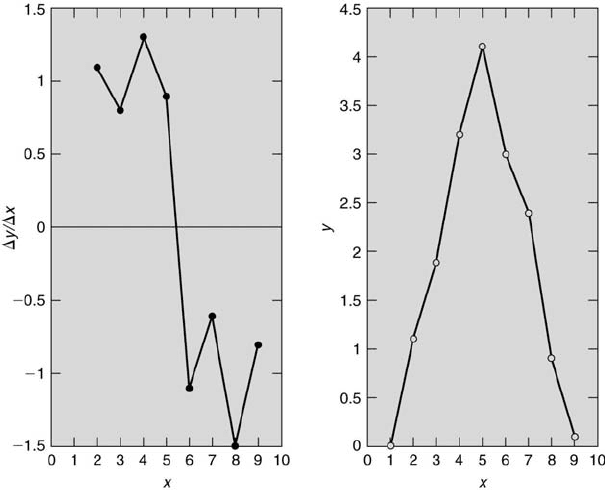
Uncertainty Analysis 269

FIGURE 7.6

The output plot of differ.m for nine (x,y) data pairs of a triangular waveform.

So, only the order of magnitude of e

can be estimated. Formally, the uncer-

tainty in a ﬁrst derivative approximated by a second-order central-diﬀerence

method is

(x)

' C

(x)

(∆x)

, (7.74)

where C

(x)

is a constant with same units as f

000

. C

(x)

can be assumed

to be of order one as a ﬁrst approximation. The important point to note is

that the discretization error is proportional to (∆x)

. So, if ∆x is reduced

by 1/2, the discretization error is reduced by 1/4.

7.12.2 *Integral Approximation

Many diﬀerent numerical methods can be used to determine the integral of

a function. The method chosen depends upon the accuracy required, if the

values of the function are known at its end points, if the numerical inte-

gration is done using equal-spaced intervals, and so forth. The trapezoidal

rule is used most commonly for situations in which the intervals are equally

spaced and the function’s values are known at its end points.

270 Measurement and Data Analysis for Engineering and Science

The trapezoidal rule approximates the area under the curve f(x) over

the interval between a and b by the area of a trapezoid,

f(x) =

(b − a)

[f(b) + f(a)] + E, (7.75)

where E = (∆x)

(x)/24, with f

(x) evaluated somewhere in the interval

from a to b. This rule can be extended to N points,

b=x

a=x

f(x)dx = ∆x[

f(x

) + f(x

) + . . . + f (x

N−1

) +

f(x

)] +

i=1

= ∆x[

i=1

f(x

) − (

f(x

) +

f(x

))] +

i=1

, (7.76)

where ∆x = (b − a)/N . The total discretization error, e

, then becomes

i=1

(∆x)

(x) =

(∆x)

(x) =

(b − a)

24N

(x). (7.77)

Thus, the uncertainty in applying the extended trapezoidal rule to approx-

imate an integral is

f(x)

' C

f(x)

N(∆x)

, (7.78)

where C

f(x)

is a constant with the same units as f

(x). C

f(x)

can be

assumed to be of order one as a ﬁrst approximation.

A numerical estimate of C

f(x)

can be made if some expression for f

(x)

can be found. A second-order central second-diﬀerence approximation can

be used, where

) =

f(x

i+1

) − 2f(x

) + f(x

i−1

)

(∆x)

. (7.79)

This introduces an additional error of O[f

0000

)(∆x)

]. So, using Equa-

tion 7.79 does not improve the accuracy of the estimate; it simply provides

a convenient way to estimate f

). Now the discretization error also can

be written alternatively as

(b − a)

24N

i=1

)(∆x)

. (7.80)

Substitution of Equation 7.79 into Equation 7.80 gives

f(x)

(b − a)

24N

{

i=1

[f(x

i+1

) − 2f(x

) + f(x

i−1

)]

}

1/2

. (7.81)

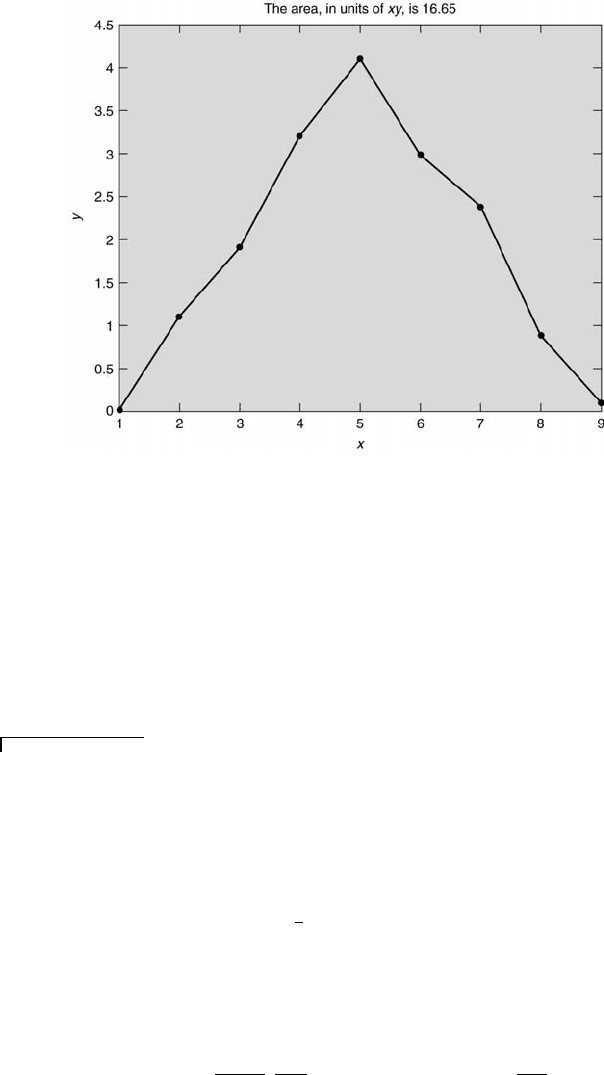
Uncertainty Analysis 271

FIGURE 7.7

The output plot of integ.m for nine (x,y) data pairs of a triangular waveform.

Note that the terms with the brackets represent the discretization errors in

the individual f

estimates, which are combined in quadrature.

The following three problems illustrate how uncertainties arising from

the ﬁnite-diﬀerence approximation of an integral factor into the uncertainty

of a result.

Example Problem 7.19

Statement: Continuing with the experiment presented in the previous example,

determine the uncertainties in the lift coeﬃcient, C

, and the drag coeﬃcient, C

of the cylinder. The lift and drag coeﬃcients are determined from 36 static pressure

measurements around the cylinder’s circumference done in 10

◦

increments.

Solution: The lift coeﬃcient is given by the equation

= −

(θ) sin(θ)dθ. (7.82)

Because there are only 36 discrete measurements of the static pressure, the integral in

Equation 7.82 must be approximated by a ﬁnite sum using the trapezoidal rule. The

uncertainty that arises from this approximation is considered in a later example in this

chapter. The general equation for the trapezoidal rule is

f(x)dx

∼

(b − a)

[

f(a)

+ f(x

) + . . . + f(x

n−1

) +

f(b)

272 Measurement and Data Analysis for Engineering and Science

Applying this formula to Equation 7.82 yields

∼

−

(θ = 0) + 2(C

(θ =

10π

180

) sin(

10π

180

)

+ . . . + C

(θ =

350π

180

) sin(

350π

180

)

+ C

(θ =

360π

180

) sin(

360π

180

)] (n = 36).

Because the uncertainty in calculating C

is an uncertainty in a result

(

∂C

)

+ (

∂C

∂ sin θ

sin θ

)

Now,

sin θ

∂ sin θ

∂θ

= u

cos θ.

Therefore,

sin θ)

+ (C

(θ)u

cos θ)

This formulation must be applied to the ﬁnite-series approximation. Doing so leads to

[(sin(θ = 0)u

)

+ (C

(θ = 0) cos(θ = 0)u

)

+(2 sin(θ =

10π

180

)

+ (2C

(θ =

10π

180

) cos(

10π

180

)

+ . . .

+(2 sin(θ =

350π

180

)

+ (2C

(θ =

350π

180

) cos(

350π

180

)

+(sin(θ =

360π

180

)

+ (C

(θ =

360π

180

) cos(

360π

180

)

]

1/2

This can be evaluated using a spreadsheet or MATLAB. For the case when u

0.021 and u

= π/360 (±0.5

◦

), u

= 0.0082. Likewise, u

can be evaluated. The

expression is similar to u

above but with cos and sin reversed. For u

= 0.021 and

= π/180 (±1.0

◦

), u

= 0.0081. Now assume that the experiment was performed

within a Reynolds number range that yields C

∼ 1. Thus, percent u

∼

0.8 %.

It is important to note that these u

and u

uncertainties do not include their ﬁnite

series approximation uncertainties. These are determined in a following example.

Example Problem 7.20

Statement: Determine the uncertainty in the drag of the cylinder that was studied

in the previous examples, where the drag, D, is deﬁned as

D ≡ C

ρV

∞

frontal

, (7.83)

with A

frontal

= d · L.

Uncertainty Analysis 273

Solution: In the experiment

ρV

∞

was measured as ∆P. Thus,

= [(

∂D

∂C

)

+ (

∂D

∂∆P

∆P

)

+ (

∂D

∂d

)

+ (

∂D

∂L

)

]

1/2

= [(∆PdLu

)

+ (C

dLu

∆P

)

+ (C

∆P Lu

)

+ (C

∆P du

)

]

1/2

Now, given that

∆P = 4 in. H

O = 996 N/m

, u

∆P

= 15 N/m

d = 1.675 in. = 0.0425 m, u

= 0.005 in. = 1.27 × 10

−4

L = 16.750 in. = 0.425 45 m, u

= 0.005 in. = 1.27 × 10

−4

∼

1, u

= 0.0092,

then

= [(996)(0.0425)(0.425 45)(0.0092)

(1)(0.0425)(0.425 45)(15)

(1)(996)(0.425 45)(1.27 × 10

−4

)

(1)(996)(0.0425)(1.27 × 10

−4

)

]

1/2

= [0.166

+ 0.271

+ 0.054

+ 0.005

]

1/2

= 0.32.

In order to get a percentage error, the nominal value of the drag is computed, where

∼

(1)(996)(0.0425)(0.42545) = 18.0 N.

Thus, the percentage error in the drag is 1.7 %, and D = 18.0 ± 0.3 N.

Example Problem 7.21

Statement: Recall the experiment presented in a previous example in which 36 static

pressure measurements were made around a cylinder’s circumference. Determine the

uncertainties in the lift and drag coeﬃcients that arise when the extended trapezoidal

rule is used to approximate the integrals involving the pressure coeﬃcient, where

= −

2π

(θ) sin(θ)dθ

(7.84)

and

= −

2π

(θ) cos(θ)dθ.

Compare these numerical uncertainties to their respective measurement uncertainties

which were obtained previously. Finally, determine the overall uncertainties in C

and

Solution: Equation 7.81 implies

f(x),C

2π

24N

{

i=1

[g(θ

i+1

) − 2g(θ

) + g(θ

i−1

)]

}

1/2

(7.85)

274 Measurement and Data Analysis for Engineering and Science

and

f(x),C

2π

24N

{

i=1

[h(θ

i+1

) − 2h(θ

) + h(θ

i−1

)]

}

1/2

where

g(θ) = C

(θ) sin(θ),

h(θ) = C

(θ) cos(θ), and

N = 36.

These uncertainties can be evaluated using a spreadsheet or MATLAB, yielding

f(x),C

= 0.0054 and u

f(x),C

= 0.0042. These uncertainties are approximately

one-half of the C

and C

measurement uncertainties.

Combining the C

and C

measurement and numerical approximation uncertainties

gives

= [0.0082

+ 0.0054

]

1/2

= 0.0098 and

= [0.0081

+ 0.0042

]

1/2

= 0.0092.

7.12.3 *Uncertainty Estimate Approximation

In some situations the direct approach to estimating the uncertainty in a

result can be complicated if the mathematical expression relating the re-

sult to the measurands is algebraically complex. An alternative approach

is to approximate numerically the partial derivatives in the uncertainty ex-

pression, thereby obtaining a more tractable expression that is amenable to

spreadsheet or program analysis.

The partial derivative term, ∂q/∂x

, can be approximated numerically

by the ﬁnite-diﬀerence expression

∂q

∂x

≈

∆q

∆x

+∆x

− q|

∆x

. (7.86)

This approximation is ﬁrst-order accurate, as seen by examining Equa-

tion 7.70. Thus, its discretization error is of order ∆xf

(x). Use of Equa-

tion 7.86 yields the forward ﬁnite-diﬀerence approximation to Equation 7.21

≈

(

∆q

∆x

)

+ (

∆q

∆x

)

+ ... + (

∆q

∆x

)

. (7.87)

The value of ∆x

is chosen to be small enough such that the ﬁnite-

diﬀerence expression closely approximates the actual derivative. Typically,

∆x

= 0.01x

is a good starting value. The value of ∆x

then should be

decreased until appropriate convergence in the value of u

is obtained.

Uncertainty Analysis 275

Example Problem 7.22

Statement: In a previous example in this chapter, the uncertainty in the density

for air was determined directly by the expression



∂ρ

∂T





∂ρ

∂P



= 2.15 × 10

−3

kg/m

where u

= 67 Pa, u

= 0.5 K, ρ = 1.19 kg/m

, T = 297 K, P = 101 325 Pa, and

air was assumed to be an ideal gas (ρ = P/RT ). Determine the uncertainty in ρ by

application of Equation 7.87.

Solution: The ﬁnite-diﬀerence expression for this case is

≈

(

∆ρ

∆P

)

+ (

∆ρ

∆T

)

where

∆ρ

∆P

= [ρ |

P +∆P

−ρ

]/∆P and

∆ρ

∆T

= [ρ |

T +∆T

−ρ

]/∆T . Letting ∆P = 0.01P

and ∆T = 0.01T yields

∆ρ

∆P

= [(P + ∆P)/RT − P/RT ]/∆P = 1/RT = ρ/P =

1.17 × 10

−5

and

∆ρ

∆T

= [P/R(T − ∆T ) − P/RT ]/∆T = −ρ/(T + ∆T ) = 3.97 × 10

−3

Substitution of these values into the equation gives u

√

0.62 × 10

−6

+ 3.93 × 10

−6

2.13 ×10

−3

kg/m

. This agrees within 1 % of the value of 2.15 ×10

−3

found using the

direct method.

7.13 *Uncertainty Based upon Interval Statistics

In some measurements situations, speciﬁc values for part or all of the data

may not be known. Rather, only a range or interval of possible values is

known. This situation introduces another type of uncertainty, that due to a

lack of knowledge about the speciﬁc values of the data, known as epistemic

uncertainty. When all other experimental uncertainties are removed, epis-

temic uncertainty still remains and becomes the overall uncertainty. Thus, a

diﬀerent approach beyond the current ISO method, which assumes lineariz-

ably small and normally distributed measurement uncertainties, is required

to handle this situation.

Ferson et al. [25] present such an approach that is based upon interval

statistics. The ISO method assumes that measurement uncertainty results

primarily from variability in the data that is caused by inherent random-

ness and/or ﬁnite sampling (termed aleatory uncertainty). Based upon this

method, additional measurements will reduce the lower bound of the uncer-

tainty estimate to the limit of design-stage uncertainties, which itself can

be minimized signiﬁcantly. However, when epistemic uncertainty is present,

the situation can be diﬀerent. The ISO method will underestimate the over-

all measurement uncertainty when epistemic uncertainty is present. Further,

additional data will not necessarily lead to a reduced uncertainty. The reader