Patrick F. Dunn, Measurement, Data Analysis, and Sensor Fundamentals for Engineering and Science, 2nd Edition

Подождите немного. Документ загружается.

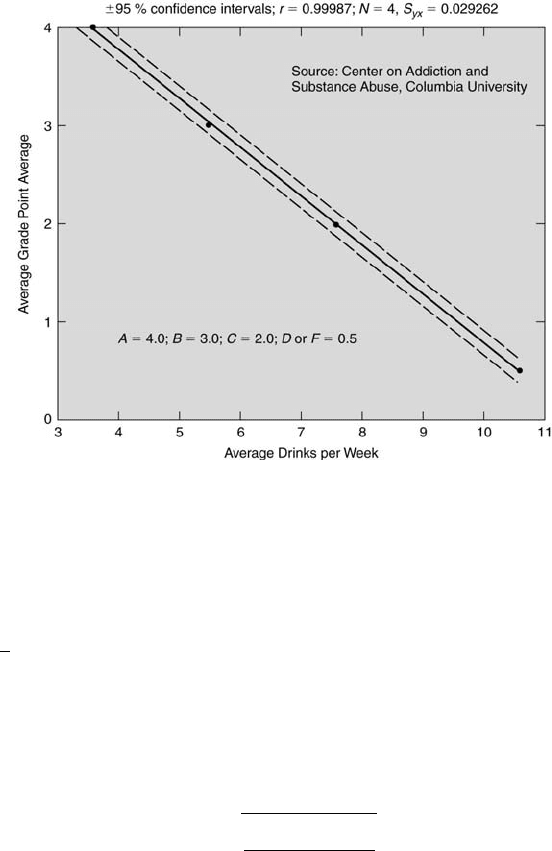
316 Measurement and Data Analysis for Engineering and Science

FIGURE 8.11

College student alcohol consumption.

When the correlation is perfect, there is no unexplained squared variation

(SSE = 0) and r = ±1. Further, when there is no ﬁt, all the y

values

are the same because they are completely independent of x. That is, all

y and, by Equation 8.21, SSE = 0. Thus, r = 0. Values of |r| > 0.99

imply a very signiﬁcant correlation; values of |r| > 0.95 imply a signiﬁcant

correlation. On the other extreme, values of |r| < 0.05 imply an insigniﬁcant

correlation; values of |r| < 0.01 imply a very insigniﬁcant correlation.

Another expression for r can be obtained which relates it to the results of

a regression analysis ﬁt. Substituting Equations 8.16 and 8.20 into Equation

8.42 yields

r =

i=1

− ¯y)

i=1

− ¯y)

. (8.43)

This equation relates r to the y

values obtained from regression analysis.

This is in contrast to Equation 8.40, which yields r directly from data. These

two equations help to underscore an important point. Correlation analysis

and regression analysis are separate and distinct statistical approaches. Each

is performed independently from the other. The results of a linear regression

analysis, however, can be used for correlation analysis.

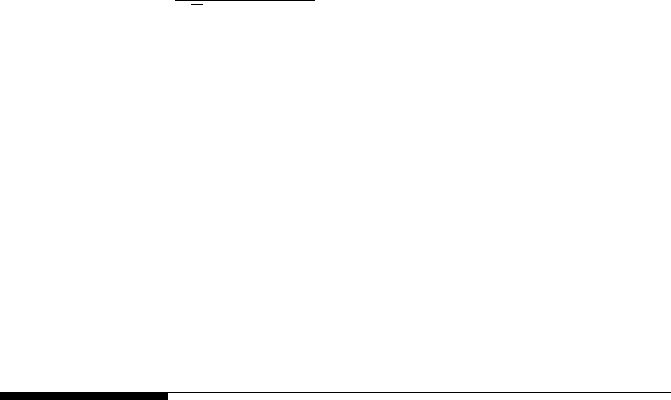
Regression and Correlation 317

Caution should be exercised in interpreting various values of the linear

correlation coeﬃcient. For example, a value of r ∼ 0 simply means that the

two variables are not linearly correlated. They could be highly correlated

nonlinearly. Further, a value of r ∼ ±1 implies that there is a strong linear

correlation. But the correlation could be casual, such as a correlation be-

tween the number of cars sold and pints of Guinness consumed in Ireland.

Both are related to Ireland’s population, but not directly to each other.

Also, even if the linear correlation coeﬃcient value is close to unity, that

does not imply necessarily that the ﬁt is the most appropriate. Although

the spring’s energy is related fundamentally to the square of its extension,

a linear correlation coeﬃcient value of 0.979 results for Case 2 in section

8.9 when correlating a spring’s energy with its extension. This high value

implies a strong linear correlation between energy and extension, but it does

not imply that a linear relation is the most appropriate one.

Finally, when attempting to establish a correlation between two variables

it is important to recognize the possibility that two uncorrelated variables

can appear to be correlated simply by chance. This circumstance makes it

imperative to go one step more than simply calculating the value of r. One

must also determine the probability that N measurements of two uncorre-

lated variables will give a value of r equal to or larger than any particular

. This probability is determined by

(| r |≥| r

|) =

2Γ[(N − 1)/2]

√

πΓ[(N − 2)/2]

(1 − r

)

(N−4)/2

dr = f(N, r), (8.44)

where Γ denotes the gamma function. If P

(| r |≥| r

|) is small, then it is

unlikely that the variables are uncorrelated. That is, it is likely that they are

correlated. Thus, 1 − P

(| r |≥| r

|) is the probability that two variables

are correlated given | r |≥| r

|. If 1 − P

(| r |≥| r

|) > 0.95, then there

is a signiﬁcant correlation, and if 1 − P

(| r |≥| r

|) > 0.99, then there

is a very signiﬁcant correlation. Values of 1 − P

(| r |≥| r

|) versus the

number of measurements, N , are shown in Figure 8.12. For example, a value

of r

= 0.6 gives a 60 % chance of correlation for N = 4 and a 99.8 % chance

of correlation for N = 25. Thus, whenever citing a value of r it is imperative

to present the percent conﬁdence of the correlation and the number of data

points upon which it is based. Reporting a value of r alone is ambiguous.

8.8 Uncertainty from Measurement Error

One of the major contributors to the diﬀerences between the measured and

calculated y values in a regression analysis is measurement error. This can

be understood best by examining the linear case.

318 Measurement and Data Analysis for Engineering and Science

FIGURE 8.12

Probability of correlation.

For an error-free experiment in which the data pairs [x

, y

] are linearly

related, the best-ﬁt relation would be

= α + βx

, (8.45)

in which α and β are the true intercept and slope, respectively, and y

is the

true mean value of y

associated with the true mean value of x

, x

. For an

experiment in which measurement errors are present one can write

= x

+ 

(8.46)

and

= y

+ 

, (8.47)

where x

and y

denote the actual, measured values and 

and 

their

measurement errors. Here, it is assumed that the value of all of the x

errors

is the same and equal to 

, and the value of all of the y

errors is the

same and equal to 

. That is, the x

and y

errors are independent of

the particular data pair. This is true if each of the y

measurements results

from an independent measurement situation. Using Equations 8.46 and 8.47,

Equation 8.45 becomes

= α + βx

+ (

− β

) = y

+ E

. (8.48)

Regression and Correlation 319

The terms in parentheses represent the error term for y

, which is denoted

by E

. Thus, the value of y

will have an error of E

with respect to its

measured value, y

. This error results from possible measurement errors in

x and y or both.

This error is characterized best through its variance, σ

. A subtle yet

important point is that the variance of x

is the same as that of 

and that

the variance of y

is the same as that of 

. This is because both x

and y

have no error. Thus, the variance in x

is characterized by the variance in its

error. This also is true for y

. These variances are denoted by σ

and σ

. If



and β

are statistically independent, then the variance of the combined

errors, σ

, is given by [4]

= σ

+ β

. (8.49)

This equation is valid only when either 

= 0 or x is controlled such that

its randomness is constrained. If either of these conditions are not met, then

cannot be subdivided into these two components. Then, the individual

contributions of the 

and 

due to the diﬀerence between the measured

and calculated value of y cannot be ascertained.

So, measurement errors lead to variances in x and y. These variances

contribute to the combined variance, σ

. It is σ

that contributes to the

diﬀerences between the y

and y

values.

8.9 Determining the Appropriate Fit

Even determining the linear best ﬁt for a set of data and its associated pre-

cision can be more involved than it appears. How to determine a linear best

ﬁt of data already has been discussed. Here, implicitly it was assumed that

the measurement uncertainties in x were negligible with respect to those

in y and that the assumed mathematical expression was the most appro-

priate one to model the data. However, many common situations involving

regression usually are more complicated. Examine the various cases that can

occur when ﬁtting data having uncertainty with a least-squares regression

analysis.

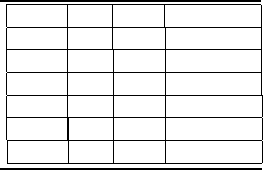
There are six cases to consider, as listed in Table 8.2. Each assumes a

level of measurement uncertainty in x, u

, and in y, u

, and whether or

not the order of the regression is correct. The term correct implies that the

underlying physical model that governs the relationship between x and y has

the same order as the ﬁt. The last two cases (5 and 6), in which both x and

y have comparable uncertainties (u

∼ u

), are more diﬃcult to analyze.

Often, only special situations of these two cases are considered [10]. Each of

the six cases is now discussed in more detail.

320 Measurement and Data Analysis for Engineering and Science

Case

Fit

correct

incorrect

6= 0

correct

6= 0

incorrect

6=0

6= 0

correct

6=0

6= 0

incorrect

TABLE 8.2

Cases involving uncertainties and the type of ﬁt.

• Case 1: This corresponds to the ideal case in which there are no uncer-

tainties in x and y (u

= u

= 0) and the order of the ﬁt is the same

as that of the underlying physical model (a correct ﬁt). For example,

consider a vertically-oriented, linear spring with a weight, W, attached

to its end. The spring will extend downward from its unloaded equilib-

rium position a distance x proportional to W, as given by Hooke’s law,

W = −kx, where k is the spring constant and negative x corresponds

to positive displacement (extension). Assuming that the experiment is

performed without error, a ﬁrst-order (linear) regression analysis would

yield a perfect ﬁt of the data with an intercept equal to zero and a slope

equal to −k. Because there are no measurement errors in either x or y,

the values of the intercept and slope will be true values, even if the data

set is ﬁnite.

• Case 2: This case involves an error-free experiment in which the data

is ﬁt with an incorrect order. For example, continuing with the spring-

weight example, the work done by the weight to extend the spring, W x,

could be plotted versus its displacement. This work equals the stored

energy of the spring, E, which equals 0.5kx

. A linear regression ﬁt of

W x versus x would result in a ﬁt that does not correspond to the correct

underlying physical model, as shown in Figure 8.13. A second-order ﬁt

would be appropriate because E ∼ x

. The resulting diﬀerences between

the data and the linear ﬁt come solely from the incorrect choice of the

ﬁt. These diﬀerences, however, easily could be misinterpreted as the

result of errors in the experiment, as is the case for the data shown in

Figure 8.13. Obviously, it is important to have a good understanding

of the most appropriate order of the ﬁt before the regression analysis is

performed.

• Case 3: For this case there is uncertainty in y but not in x and the

correct order of the ﬁt is used. This is the type of situation encountered

when regression analysis ﬁrst was considered. The resulting diﬀerences

between the measured and calculated y values result from the measure-

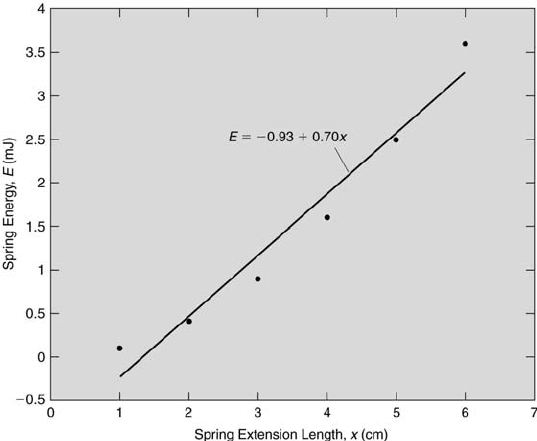
Regression and Correlation 321

FIGURE 8.13

Example of Case 2.

ment uncertainties in y. Consequently, a correct regression ﬁt will agree

with the data to within its measurement uncertainty.

When the correct physical model is not known a priori, the standard

approach is to increase the order of the ﬁt within reason until an accept-

able ﬁt is obtained. What is acceptable is somewhat arbitrary. Ideally,

all data points inclusive of their uncertainties should agree with the ﬁt

to within the conﬁdence intervals speciﬁed by Equation 8.30. Although

an n-th order polynomial will ﬁt n-1 data points exactly, this usually

does not correspond to a physically-realizable model. Very seldom does a

physical law involve more than a fourth power of a variable. In fact, high-

degree polynomial ﬁts characteristically exhibit large excursions between

data points and have coeﬃcients that require many signiﬁcant ﬁgures

for repeatable accuracy [13]. So, caution should be exercised when using

higher-order ﬁts. Whenever possible, the order of the ﬁt should corre-

spond to the order of the physical model.

• Case 4: This case considers the situation in which there is uncertainty

in y but not in x and an incorrect order of the ﬁt is used. Two un-

certainties in the calculated y values result in relation to the true ﬁt.

One is from the measurement uncertainty in y and the other is from the

use of an incorrect model. Here it is diﬃcult to determine directly the

contribution of each uncertainty to the overall uncertainty. A systematic

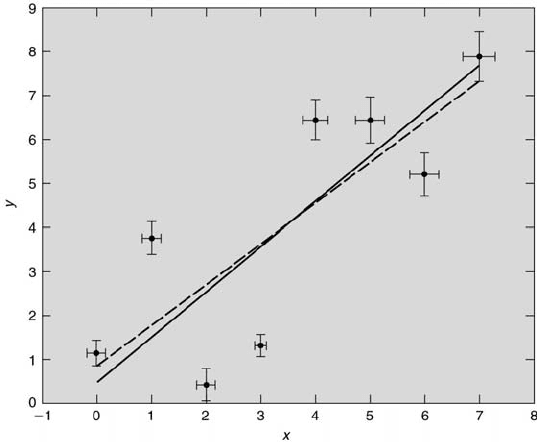
322 Measurement and Data Analysis for Engineering and Science

FIGURE 8.14

Two regression ﬁts of the same data.

study involving either more accurate measurements of y or the use of a

diﬀerent model would be necessary to determine this.

Finally, there are two other cases that arise in which there is uncertainty

in both x and y. The presence of both of these uncertainties leads to a best

ﬁt that is diﬀerent from that when there is only uncertainty in y. This is

illustrated in Figure 8.14 in which two regression ﬁts are plotted for the same

data. The dashed line represents the ﬁt that considers only the uncertainty

in y that was established using a linear least-squares regression analysis.

The solid line is the ﬁt that considers uncertainty in both x and y that

was established using Deming’s method (see [9]), which is considered in the

following case. It is easy to see that when uncertainty is present in both x

and y, a ﬁt established using the linear least-squares regression analysis that

does not consider the uncertainty in x will not yield the best ﬁt.

Whenever u

∼ u

and no further constraints are placed on them, more

extensive regression techniques must be used to determine the best ﬁt of

the data (for example, see [3]). This topic is beyond the scope of this text.

However, Mandel [10] has examined two special and practical situations

in which uncertainty is present in x and linear regression analysis can be

applied. These will now be examined.

• Case 5: The general situation for this case involves uncertainties in both

x and y and a correct order of the ﬁt.

Regression and Correlation 323

For the ﬁrst special situation in which the ratio of the variances of the

x and y errors, λ = σ

/σ

, is known a priori, a linear best-ﬁt equation

can be determined using Deming’s method of minimizing the weighted

sum of squares of x and y. Further, estimates of the variances of the x

and y can be obtained.

The slope of the regression line calculated by this method is

b =

λS

− S

− λS

)

+ 4λS

2λS

, (8.50)

and the intercept is given by the normal Equation 8.19.

The estimates for the variances of the x and y errors are, respectively,

= (

1 + λb

)

− 2bS

+ b

N − 2

(8.51)

and

= (

1 + λb

)

− 2bS

+ b

N − 2

. (8.52)

Note that Equations 8.51 and 8.52 diﬀer only by the factor λ. These

equations can be used to estimate the ﬁnal uncertainties in x and y for

P percent conﬁdence. These are the uncertainties in estimating x and y

from the ﬁt (as opposed to the measurement uncertainties in x and y).

They are

final

= t

N−2,P

(8.53)

and

final

= t

N−2,P

. (8.54)

Using these equations, a regression ﬁt can be plotted with data and its

error bars, as shown in Figure 8.15, in addition to determining values

of λ, u

final

and u

final

. These values are 0.25, ±4.0985, and ±2.0492,

respectively, for the data presented in the ﬁgure. The estimates for the

variances of x and y are

= 0.7014 and

= 2.8055. The estimates of

the ﬁnal uncertainties in x and y appear relatively large at ﬁrst sight.

This is the result of the relatively large scatter in the data. So, for a

speciﬁed value of x in this case, the value of y will be within ±4.0985

of its best-ﬁt value 95 % of the time. Likewise, for a speciﬁed value of

y, the value of x will be within ±2.0492 of its best-ﬁt value 95 % of the

time.

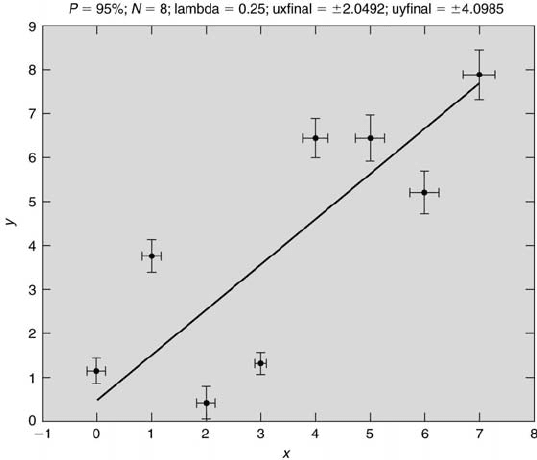
324 Measurement and Data Analysis for Engineering and Science

FIGURE 8.15

Example of Case 5 when λ is known.

The second special situation considers when x is a controlled variable.

This is known as the Berkson case, in which the value of x is set as close

as possible to its desired value, thereby constraining its randomness. This

corresponds, for example, to a static calibration in which there is some

uncertainty in x but the value of x is speciﬁed for each calibration point.

For this situation a standard linear least-squares regression ﬁt of the

data is valid. Further, estimates can be made for all of the uncertainties

presented beforehand for Case 3. The interpretation of the uncertainties,

however, is somewhat diﬀerent [10]. The uncertainty in y with respect

to the regression ﬁt must be interpreted according to Equation 8.49.

• Case 6: This is the most complicated case in which there are uncertain-

ties in both x and y and an incorrect order of the ﬁt is used. The same

analytical approaches can be taken here as were done for the special

situations in Case 5. However, the interpretation of the uncertainties is

confounded further as a result of the additional uncertainty introduced

by the incorrect order of the ﬁt.

Regression and Correlation 325

8.10 *Signal Correlations in Time

Thus far, the application of correlation analysis to discrete information has

been considered. Correlation analysis also can be applied to information

that is continuous in time.

Consider two signals, x(t) and y(t), of two experimental variables. As-

sume that these signals are statistically stationary and ergodic. These terms

are deﬁned in Chapter 9. For a stationary signal, the statistical properties

determined by ensemble averaging values for an arbitrary time from the be-

ginning of a number of the signal’s time history records are independent of

the time chosen. Further, if these average values are the same as those found

from the time-average over a single time history record, then the signal is

also ergodic. So, an ergodic signal is also a stationary signal. By examin-

ing how the amplitude of either signal’s time history record at some time

compares to its amplitude at another time, important information, such as

on the repeatability of the signal, can be gathered. This can be quantiﬁed

through the autocorrelation function of the signal, which literally correlates

the signal with itself (thus the preﬁx auto). The amplitudes of the signals

also can be compared to one another to examine the extent of their co-

relation. This is quantiﬁed through the cross-correlation function, in which

the cross product of the signals is examined.

8.10.1 *Autocorrelation

For an ergodic signal x(t), the autocorrelation function is the average value

of the product x(t) · x(t + τ), where τ is some time delay. Formally, the

autocorrelation function, R

(τ), is deﬁned as

(τ) ≡ E[x(t) · x(t + τ)] = lim

T →∞

x(t)x(t + τ )dt. (8.55)

Because the signal is stationary, R

(τ), its mean and its variance are inde-

pendent of time. So,

E[x(t)] = E[x(t + τ)] = x

(8.56)

and

x(t)

= σ

x(t+τ)

= σ

= E[x

(t)] − x

. (8.57)

Analogous to Equation 8.33, the autocorrelation coeﬃcient can be

deﬁned as

(τ) ≡

E[(x(t) − x

)(x(t + τ ) − x

)]

. (8.58)