Patrick F. Dunn, Measurement, Data Analysis, and Sensor Fundamentals for Engineering and Science, 2nd Edition

Подождите немного. Документ загружается.

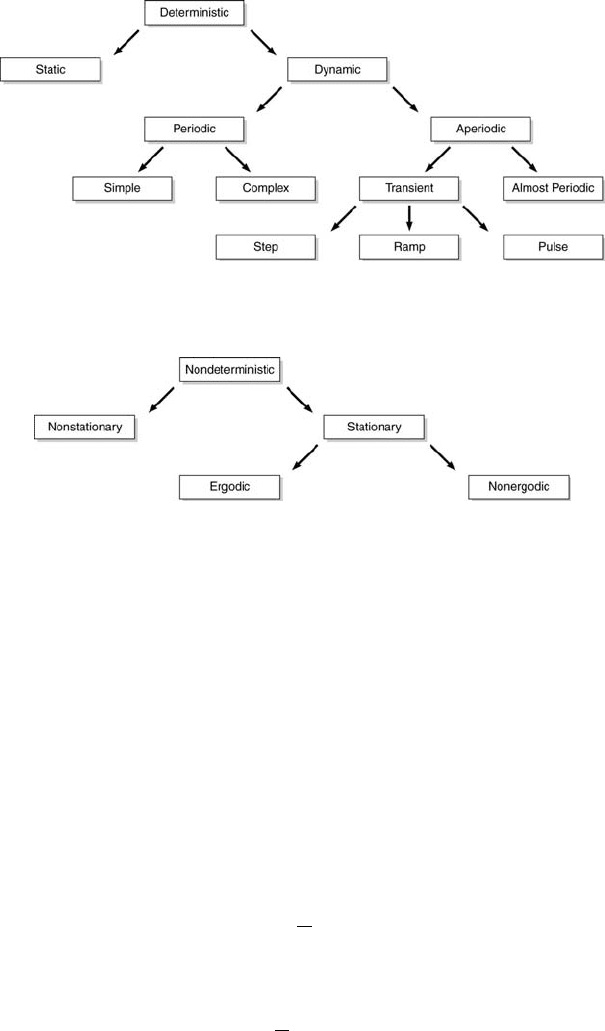
346 Measurement and Data Analysis for Engineering and Science

FIGURE 9.2

Deterministic signal subdivisions (adapted from [2]).

FIGURE 9.3

Nondeterministic signal subdivisions (adapted from [2]).

when only µ

) = µ

and R

, t

+ τ) = R

(τ), that is, when only the

signal’s ensemble mean and autocorrelation function are time invariant. In a

more restrictive sense, if all other ensemble higher-order moments and joint

moments (see Chapter 5 for more about moments) also are time invariant,

the signal is strongly stationary (stationary in the strict sense). So, the

term stationary means that each of a signal’s ensemble-averaged statistical

properties are constant with respect to t

. It does not mean that the am-

plitude of the signal is constant over time. In fact, a random signal is never

completely stationary in time!

For a single time history, the temporal mean value, µ

, and the temporal

autocorrelation coeﬃcient, R

(τ), are

= lim

T →∞

x(t)dt (9.4)

and

(τ) = lim

T →∞

x(t)x(t + τ )dt. (9.5)

For most stationary data, the ensemble averages at an arbitrary time, t

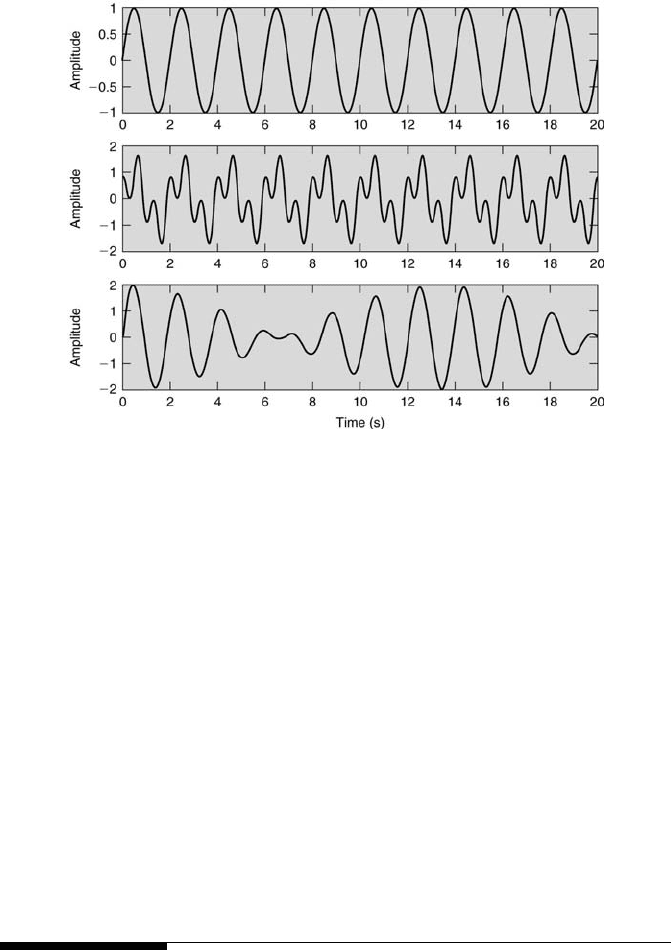
Signal Characteristics 347

FIGURE 9.4

Various signals comprised of sines and cosines.

will equal their corresponding temporal averages computed for an arbitrary

single time history in the ensemble. When this is true, the signal is ergodic.

If the signal is periodic, then the limits in Equations 9.4 and 9.5 do not ex-

ist because averaging over one time period is suﬃcient. Ergodic signals are

important because all of their properties can be determined by perform-

ing time averages over a single time history record. This greatly simpliﬁes

data acquisition and reduction. Most random signals representing stationary

physical phenomena are ergodic.

A ﬁnite record of data of an ergodic random process can be used in

conjunction with probabilistic methods to quantify the statistical properties

of an underlying process. For example, it can be used to determine a random

variable’s true mean value within a certain conﬁdence limit. These methods

also can be applied to deterministic signals, which are considered next.

9.3 Signal Variables

Most waveforms can be written in terms of sums of sines and cosines, as will

be shown later in Section 9.5. Before examining more complex waveform

expressions, the variables involved in simple waveform expressions must be

348 Measurement and Data Analysis for Engineering and Science

deﬁned. This can be done by examining the following expression for a simple,

periodic sine function,

y(t) = C sin(nωt + φ) = C sin(2πnft + φ), (9.6)

in which the argument of the sine is in units of radians. The variables and

their units (given in brackets) are as follows:

• C: amplitude [units of y(t)]

• n: number of cycles [dimensionless]

• ω: circular frequency [rad/s]

• f : cyclic frequency [cycles/s = Hz]

• t: time [s]

• T : period (= 2π/ω = 1/f) [s/cycle]

• φ: phase [rad] where φ = 2π(t/T ) = 2π(θ

◦

/360

◦

)

Also note that 2π rad = 1 cycle = 360

◦

and sin(ωt+π/2) = cos(ωt). The top

plot in Figure 9.4 displays the signal y(t) = sin(πt). Its period equals 2π/π

= 2 s, as seen in the plot. The above deﬁnitions can be applied readily to

determine the frequencies of a periodic signal, as in the following example.

Example Problem 9.1

Statement: Determine the circular and cyclic frequencies for the signal y(t) =

10 sin(628t).

Solution: Using the above deﬁnitions,

circular frequency, ω = 628 rad/s (assuming n = 1 cycle), and

cyclic frequency, f = ω/2π = 628/2π = 100 cycles/s= 100 Hz.

When various sine and cosine waveforms are combined by addition, more

complex waveforms result. Such waveforms occur in many practical situ-

ations. For example, the diﬀerential equations describing the behavior of

many systems have sine and cosine solutions of the form

y(t) = A cos(ωt) + B sin(ωt). (9.7)

By introducing the phase angle, φ, y(t) can be expressed as either a cosine

function,

y(t) = C cos(ωt − φ), (9.8)

Signal Characteristics 349

or a sine function,

y(t) = C sin(ωt − φ + π/2) = C sin(ωt + φ

∗

), (9.9)

where C, φ, and φ

∗

are given by

C =

+ B

, (9.10)

φ = tan

−1

(B/A), (9.11)

and

∗

= tan

−1

(A/B), (9.12)

noting that φ

∗

= (π/2) − φ. Reducing the waveform in Equation 9.7 to

either Equation 9.8 or Equation 9.9 often is useful in interpreting results.

The middle plot in Figure 9.4 shows the signal y(t) = sin(πt) + 0.8 cos(3πt).

This signal is complex and has two frequencies, ω

= π and ω

= 3π rad/s.

This leads to two periods, T

= 2 s and T

= 2/3 s. Because T

= 3T

, the

period T

will contain one cycle of sin(ω

t) and three periods of 0.8 cos(ω

t).

So, T

= 2 s is the fundamental period of this complex signal. In general, the

fundamental period of a complex signal will be the least common multiple

of the contributory periods.

An interesting situation arises when two waves of equal amplitude and

nearly equal frequencies are added. The resulting wave exhibits a relatively

slow beat with a frequency called the beat frequency. In general, the sum

of two sine waves of frequencies, f and f + ∆f, combines trigonometrically

to yield a signal whose amplitude is modulated as the cos(∆f /2). The fre-

quency ∆f/2 is deﬁned conventionally as the beat frequency. An example of

the resultant beating for the signal y(t) = sin(πt) + sin(1.15πt) is displayed

in the bottom plot of Figure 9.4. As can be seen, the signal repeats itself ev-

ery 13.33 s. This corresponds to a cyclic frequency of 0.075 Hz, which equals

∆f/2 (0.15/2). The phenomenon of producing a signal (wave) having a new

frequency from the mixing of two signals (waves) is called heterodyning

and is used in tuning musical instruments and in laser-Doppler velocimeters.

9.4 Signal Statistical Parameters

Signals can be either continuous in time or discrete. Discrete signals usually

arise from the digitization of a continuous signal, to be discussed in Chap-

ter 10, and from sample-to-sample experiments, which were considered in

Chapter 7. A large number of statistical parameters can be determined from

either continuous or discrete signal information. The parameters most fre-

quently of interest are the signal’s mean, variance, standard deviation, and

rms. For continuous signals, these parameters are computed from integrals

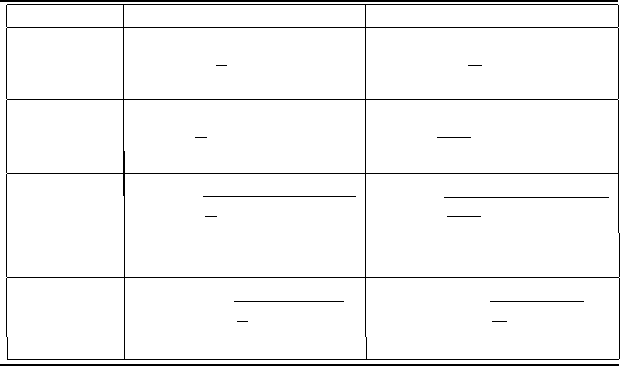
350 Measurement and Data Analysis for Engineering and Science

Quantity

Continuous

Discrete

Mean

¯x =

x(t)dt

¯x =

i=1

Variance

[x(t) − ¯x]

N−1

i=1

− ¯x]

Standard

[x(t) − ¯x]

N−1

i=1

− ¯x]

Deviation

rms

x(t)

rms

i=1

TABLE 9.1

Statistical parameters for continuous and discrete signals.

of the signal over time. For discrete signals, these parameters are deter-

mined from summations over the number of samples. The expressions for

these properties are presented in Table 9.1. Note that as T → ∞ or N → ∞,

the statistical parameter values approach the true values of the underlying

process.

The choice of a time period that is used to determine the statistical pa-

rameters of a signal, called the signal sample period, depends upon the

type of waveform. When the waveform is periodic, either simple or complex,

the signal sample period should be the fundamental period. When the wave-

form is almost periodic or nondeterministic, no single signal sample period

will produce exact results. For this situation, it is best to keep increasing

the signal’s sample period until the statistical parameter values of interest

become constant to within acceptable limits.

Determining an appropriate sample period is not always straightforward.

The values of the running mean, variance, skewness, and kurtosis of two data

samples are shown in Figure 9.5. The adjective running implies that the

value of a statistical moment is averaged over the time period from an initial

time to each time of interest. The ﬁrst sample, indicated by solid curves,

was drawn randomly from a normal population having a mean value of 3.0

and a standard deviation of 0.5. The second sample, indicated by dotted

curves, was the same as the ﬁrst but with an additional amplitude decrease

in time equal to 0.001/s. The mean of the ﬁrst sample reaches its ﬁnal value

at approximately 100 s. The mean of the second sample exhibits a decrease

in time, which is linear after approximately 100 s. The variance, skewness,

Signal Characteristics 351

FIGURE 9.5

Statistical properties versus sample time.

and kurtosis values of both samples vary with respect to sample time and

between samples during most of the entire sample time. The variances of the

two samples agree up to approximately 300 s. Then, they deviate from one

another because of the second sample’s mean value decrease in time. This

example illustrates the complexity in determining an appropriate sample

time, especially if the signal being sampled has a gradual change in time

over the sample period in addition to short-time ﬂuctuations.

Sometimes it is important to examine the ﬂuctuating component of a

signal. The average value of a signal (its DC component) can be subtracted

from the original signal to reveal more clearly the signal’s ﬂuctuating be-

havior (its AC component). This is shown in Figure 9.6, in which the left

plot is the complete signal (DC plus AC components), the middle plot is

the DC component and the AC component, each shown separately, and the

right plot is the AC component ampliﬁed 10 times.

The concepts of the mean, variance, and standard deviation were pre-

sented in Chapter 5. The root mean square (rms) is another important

statistical parameter. It is deﬁned as the positive square root of the mean of

the squares. Its continuous and discrete representations are presented in Ta-

ble 9.1. The rms characterizes the dynamic portion (AC component) of the

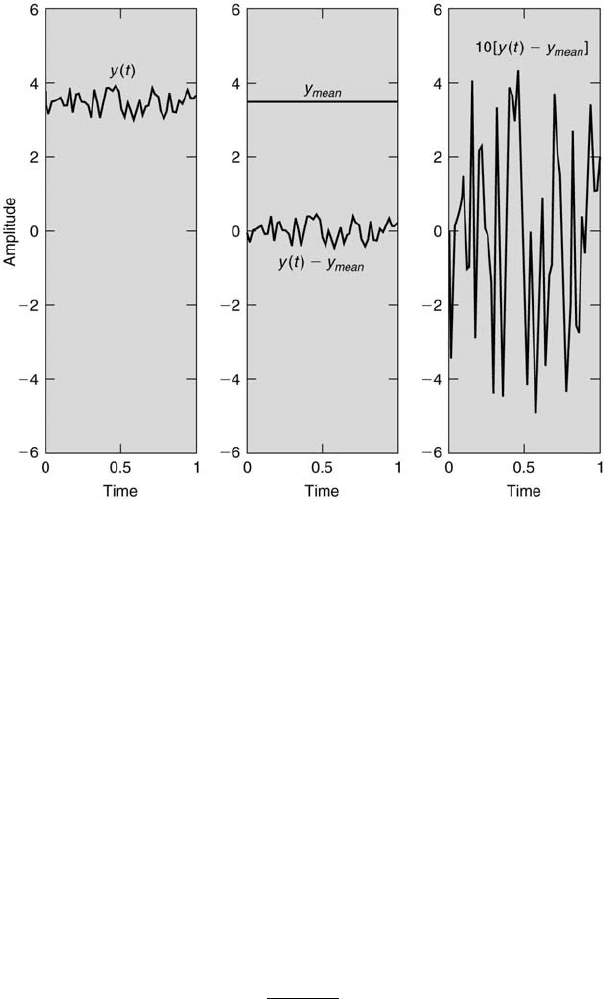
352 Measurement and Data Analysis for Engineering and Science

FIGURE 9.6

Subtraction of the mean value from a signal.

signal and the mean characterizes its static portion (DC component). The

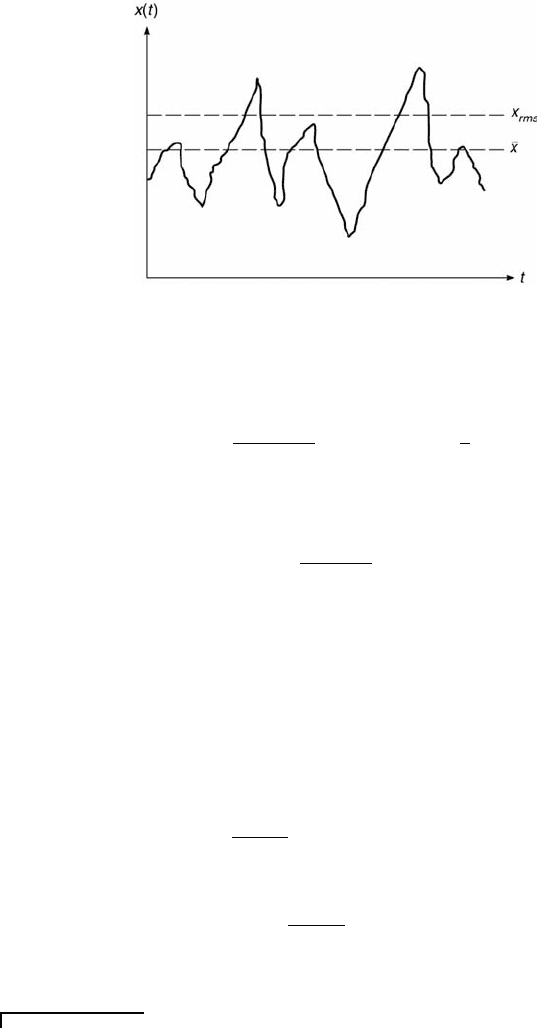
magnitudes of these components for a typical signal are shown in Figure 9.7.

When no ﬂuctuation is present in the signal, x(t) is constant and equal to

its mean value, ¯x. So, x

rms

≥ ¯x always. x

rms

is the temporal average of the

square of the amplitude of x.

The following two applications of the rms concept show its utility:

1. The total energy dissipated over a period of time by a resistor in a circuit

P (t)dt = R

[I(t)]

dt = R(t

− t

rms

, (9.13)

where

rms

− t

)

[I(t)]

dt. (9.14)

2. The temporal-averaged kinetic energy per unit volume in a ﬂuid at a

point in a ﬂow is

Signal Characteristics 353

FIGURE 9.7

A signal showing its mean and rms values.

E =

2(t

− t

)

[U(t)]

dt =

ρU

rms

, (9.15)

where

rms

− t

)

[U(t)]

dt. (9.16)

Sometimes, the term rms refers to the rms of the ﬂuctuating component

of the signal and not to the rms of the signal itself. For example, the ﬂuc-

tuating component of a ﬂuid velocity, u(t), can be written as the diﬀerence

between a total velocity, U(t), and a mean velocity,

U(t), as

u(t) = U (t) −

U(t). (9.17)

So, the rms of the ﬂuctuating component is

rms



− t

{U(t) −

U(t)}



1/2

, (9.18)

where

U(t) =

− t

U(t)dt. (9.19)

By comparing Equations 9.16 and 9.18, it is evident that U

rms

6= u

rms

Example Problem 9.2

Statement: Determine the rms of the ramp function y(t) = A(t/T ) in which A is

the amplitude and T is the period.

354 Measurement and Data Analysis for Engineering and Science

Solution: Because y(t) is a deterministic periodic function, the rms needs to be

computed for only one period, from t = 0 to t = T . Application of the rms equation

from Table 9.1 for y(t), which is a continuous signal, yields

rms

= [

− t

)

dt]

1/2

− t

)

− t

)

For t

= 0 and t

= T , the rms becomes

rms

√

What is ¯y(t)? (Answer: A/2) What is the rms of a sine wave of amplitude A? (Answer:

√

9.5 Fourier Series of a Periodic Signal

Before considering the Fourier series, the deﬁnition of orthogonality must

be examined. The inner product (dot product), (x, y), of two real-valued

functions x(t) and y(t) over the interval a ≤ t ≤ b is deﬁned as

(x, y) =

x(t)y(t)dt. (9.20)

If (x, y) = 0 over that interval, then the functions x and y are orthogonal

in the interval. If each distinct pair of functions in a set of functions is

orthogonal, then the set of functions is mutually orthogonal.

For example, the set of functions sin(2πmt/T ) and cos(2πmt/T ), m =

1, 2, ..., form one distinct pair and are mutually orthogonal because

T/2

−T/2

sin(2πmt/T ) cos(2πnt/T )dt = 0 for all m, n. (9.21)

Also, these functions satisfy the other orthogonality relations

y(t) =

T/2

−T/2

cos(2πmt/T ) cos(2πnt/T )dt =



0 m 6= n

T m = n

(9.22)

and

y(t) =

T/2

−T/2

sin(2πmt/T ) sin(2πnt/T )dt =



0 m 6= n

T m = n.

(9.23)

Knowing these facts is useful when performing certain integrals, such as

those that occur when determining the Fourier coeﬃcients.

Signal Characteristics 355

Fourier analysis and synthesis, named after Jean-Baptiste-Joseph Fourier

(1768-1830), a French mathematician, now can be examined. Fourier showed

that the temperature distribution through a body could be represented by

a series of harmonically related sinusoids. The mathematical theory for this,

however, actually was developed by others [3]. Fourier methods allow com-

plex signals to be approximated in terms of a series of sines and cosines.

This is called the trigonometric Fourier series. The Fourier trigonometric

series that represents a signal of period T can be expressed as

y(t) =

∞

n=1



cos



2πnt



+ B

sin



2πnt



, (9.24)

where

T/2

−T/2

y(t)dt, (9.25)

T/2

−T/2

y(t) cos



2πnt



dt n = 1, 2, ..., (9.26)

and

T/2

−T/2

y(t) sin



2πnt



dt n = 1, 2, ... . (9.27)

The frequencies associated with the sines and cosines are integer multi-

ples (n-th harmonics) of the fundamental frequency. The fundamental

or primary frequency, the ﬁrst harmonic, is denoted by n = 1, the sec-

ond harmonic by n = 2, the third harmonic by n = 3, and so on. A

twice the average of y(t) over one period. A

and B

are called the Fourier

coeﬃcients of the Fourier amplitudes. The expression for A

can be deter-

mined by multiplying both sides of the original series expression for y(t) by

cos(2πnt/T ), then integrating over one period from t = −T /2 to t = T/2.

The expression for B

is found similarly, but instead, by multiplying by

sin(2πnt/T ). This is called Fourier’s trick.

The procedure by which the Fourier amplitudes for any speciﬁed y(t) are

found is called Fourier analysis. Fourier analysis is the analog of a prism

that separates white light (a complex signal) into colors (simple periodic

sine functions). Fourier synthesis is the reverse procedure by which y(t)

is constructed from a series of appropriately weighted sines and cosines. The

Fourier synthesis of a signal is useful because the amplitude and frequency

components of the signal can be identiﬁed.

A Fourier series representation of y(t) exists if y(t) satisﬁes the following

Dirichlet conditions:

1. y(t) has a ﬁnite number of discontinuities within the period T (it is

piece-wise diﬀerentiable).