Пчельник В.К. Пособие по курсу высшая математика. Матрицы и определители

21 22

интерес тот случай, когда однородная система имеет ненулевое

решение.

Для того, чтобы однородная система ЛАУ имела ненуле-

вое решение, необходимо и достаточно, чтобы ранг матрицы

системы был меньше числа неизвестных, то есть, чтобы

r(A)<n.

Для того, чтобы однородная система n линейных уравне-

ний с n неизвестными имела ненулевой решение, необходимо и

достаточно, чтобы ее определитель был равен нулю.

Самым универсальным методом решения систем ЛАУ

является метод Гаусса, состоящий в последовательном исклю-

чении неизвестных. В результате прямого хода метода Гаусса

посредством элементарных преобразований система приводит-

ся к

ступенчатому (в частности, треугольному) виду:

⎪

⎩

⎪

⎨

⎧

=++

=+++

=++++

....

.......................................................

,......

33333

22323222

11331212111

knknkkk

nn

dxcxc

dxcxcxc

dxcxcxcxc

(2)

Если в процессе преобразований появляются нулевые

уравнения, то есть равенства вида

0=0, то их отбрасывают.

Если появляются уравнения вида

0=b

i

, b

i

≠0, то система не име-

ет решения.

Обратный ход метода Гаусса заключается в нахождении

неизвестных из системы (2). Здесь возможны два случая:

1)

если k=n, то исходная система имеет единственное реше-

ние;

2)

k<n. В этом случае объявляем неизвестные x

k+1

,…, x

n

сво-

бодными (они могут принимать любые значения) и выра-

жаем переменные

x

1

, x

2

,…, x

n

(базисные) через свободные.

В этом случае система имеет бесконечно много решений.

Если однородная система ЛАУ имеет ненулевое реше-

ние, то в этом случае одна имеет бесконечно много решений.

Из множества решений однородной системы можно выбрать

базис. Таким образом, любое решение однородной системы

будет являться линейной комбинацией элементов базиса. Лю-

бой

такой базис называется фундаментальной системой реше-

ний (ФСР) однородной системы линейных уравнений. ФСР

существует тогда и только тогда, когда

r(A)<n и содержит (r-n)

решений. ФСР может быть найдена следующим образом.

Выделим базисный минор и базисные неизвестные

x

1

,

x

2

,…, x

r

, которые линейно выражаются через свободные пере-

менные

x

r+1

,…, x

n

:

⎪

⎩

⎪

⎨

⎧

+++=

−++

....

....................................................

,...

2211

12121111

nrrnrrrrr

nrnrr

xxxx

βββ

Выделим частные решения однородной системы по следую-

щему принципу. Для нахождения первого вектора-решения

примем значения свободных переменных

x

r+1

=1,

x

r+2

= x

r+3

=…=x

n

=0. Для нахождения второго вектора-решения

полагаем

x

r+2

=1, а остальные (r-1) свободные переменные по-

лагаем равными нулю и т.д. Таким образом, ФСР в векторной

форме будет иметь вид

(

)

()

.1 ,0 ..., ,0 ,,...,,

..............................................

,0 ..., 0, ,1 ,0 ,,...,,

,0 ..., 0, ,0 ,1 ,,...,,

2 1

222122

121111

rnrrnrnrn

r

x

−−−−

=

βββ

2.1. Примеры решения типовых задач

Пример 1. Решить систему методом обратной матрицы и

по формуле Крамера:

23 24

⎪

⎩

⎪

⎨

⎧

=+−

−=+−

=+−

.1

,135

,342

321

xxx

Решение. Проверим систему на невырожденность:

.08

111

351

142

A det ≠−=

−

=

Значит, система имеет единственное решение. Найдем

обратную матрицу. Сначала вычислим все алгебраические до-

полнения:

.6

51

42

,2

31

12

,7

35

14

,2

11

42

,1

11

12

,3

11

14

,4

11

51

,2

11

31

,2

11

35

333231

232221

131211

−=

−

==−==

−

=

−=

−

−====

−

−=

=

−

==−=−=

−

=

AAA

Тогда

⎟

⎠

⎞

⎜

⎝

⎛

−−

−

−−

−=

−

624

512

732

8

1

A

.

Для решения системы воспользуемся формулой

:

1

bAx

−

=

,

1

0

2

8

0

16

8

1

16)1(234

15)1(132

17)1(332

8

1

3

624

512

732

8

1

⎟

⎠

⎞

⎜

⎝

⎛

−

=

⎟

⎠

⎞

⎜

⎝

⎛

−

−=

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅−−⋅−⋅

⋅−−⋅+⋅

−

−=

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

−−

−

−−

−=x

то есть, х

1

=2, х

2

=0, х

3

=-1.

Решим систему по формуле Крамера:

.8

111

151

342

,0

111

311

132

,16

111

351

143

,8 det

:3,1 ,

321

=

−

−−

−

=Δ=−=Δ−=

−

−−

−

=Δ

−=

=

Δ

=

A

ix

i

Тогда

.1

8

,0

8

0

,2

8

16

321

−=

−

==

−

==

−

= xxx

Пример 2. Найти решение системы:

⎪

⎩

⎪

⎨

⎧

=−+

−=+−

=++

.74

,11332

,2

,724

321

xxx

Решение. Запишем расширенную матрицу системы, а за-

тем с помощью элементарных преобразований строк будем

приводить ее к трапецевидной форме:

25 26

~

15

2

550

360

111

~

7

11

7

2

114

332

124

111

~

7

11

2

7

114

332

111

124

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

−

.

1

5

2

100

120

111

~

3

5

2

110

120

111

~

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

−

Сначала вторая строка была поставлена первой, чтобы

разрешающий элемент

а

11

был равен 1. Затем первая строка

полученной матрицы поэлементно умножалась на (-4) и скла-

дывалась со второй и четвертой строками, а также умноженная

на

(-2) складывалась поэлементно с третьей строкой. В результате

получилась матрица, в которой под элементом

а

11

=1 стоят все

нули в первом столбце.

Поделив элементы второй строки на 2, а третьей и чет-

вертой ― на 5 и отбросив одну из одинаковых строк, получим

матрицу из трех строк. На данном шаге разрешающей стано-

вится вторая строка и элемент

а

22

=2. Умножая элементы треть-

ей строки на (-2) и прибавляя к полученной третьей строке вто-

рую, мы привели матрицу к требуемому виду. Полученной

матрице соответствует система

⎪

⎩

⎪

⎨

⎧

−=

=−

−=+−

.1

,52

,2

3

32

321

x

xx

xxx

Отсюда получаем, что

х

1

=1, х

2

=2, х

3

=-1.

Пример 3. Найти решение системы:

⎪

⎩

⎪

⎨

⎧

=+++

=++

=+++

=+−+

.552

,38 42

,142

,032

4321

421

4321

xxxx

xxx

xxxx

Решение. Запишем расширенную матрицу системы, а за-

тем с помощью элементарных преобразований строк приведем

ее к трапецевидной форме:

~

5

3

1

0

2200

1200

3121

~

5

3

1

0

5121

8042

4121

3121

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

−

.

8

4

1

0

0000

2000

1200

3121

~

8

4

1

0

2000

1200

3121

~

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

−

Соответствующая система уравнений будет иметь вид:

⎪

⎩

⎪

⎨

⎧

=

=+

=+−+

.80

,42

,12

,032

4

43

4321

x

xx

xxxx

Так как последние два уравнения системы противоречивы, то

система не совместима.

Пример 4. Найти решение системы:

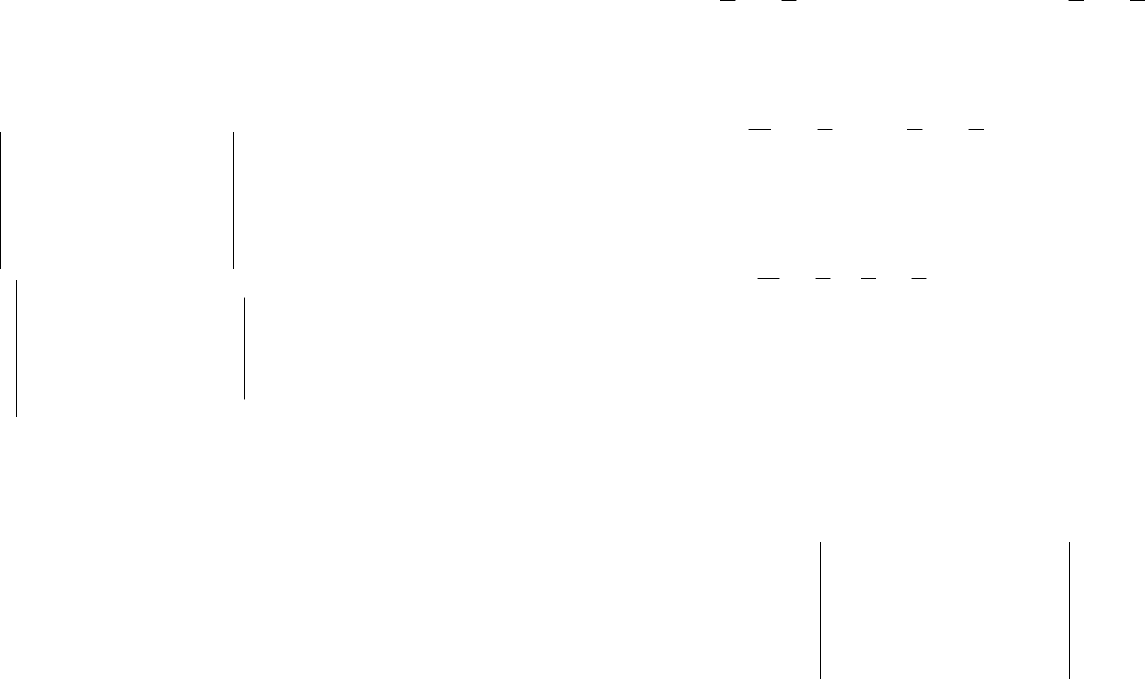
27 28

⎪

⎩

⎪

⎨

⎧

=+−−

=−++

=−+−

=−++

.2225

,551035

,343

,1232

4321

xxxx

Решение. Запишем расширенную матрицу системы, а за-

тем с помощью элементарных преобразований строк будем

приводить ее к трапецевидной форме:

~

1

0

1

4570

5570

2321

~

2

5

3

1

2251

51035

1413

2321

⎟

⎠

⎞

⎜

⎝

⎛

−−

−

⎟

⎠

⎞

⎜

⎝

⎛

−−

−

−−

−

.

1-

0

1

1000

55-7-0

2-321

~

1

0

1

1000

0000

5570

2321

~

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

−

−−

−

Для получения второй матрицы вычитаем из второй

строки первую, умноженную на 3, из третьей строки ― пер-

вую, умноженную на 5, из четвертой строки ― первую. Для

получения следующей матрицы последовательно вычитаем из

второй строки третью и четвертую и, исключив из матрицы

нулевую строку, получим, что соответствующая последней

матрице система будет иметь вид

⎪

⎩

⎪

⎨

⎧

−=

=+−−

=−++

.1

,0557

,1232

4

432

4321

x

xxx

xxxx

В полученной системе число уравнений меньше числа

неизвестных. Следовательно, система будет иметь бесконечно

много решений. Получаем, что

).1(23

7

5

7

5

21221 ,

7

5

7

5

,1

3

3421324

−+−

−

⎟

⎠

⎞

⎜

⎝

⎛

−−−=+−=−−=−=

x

xxxxxxx

То есть,

.1 ,

7

5

7

5

,

7

3

7

11

43231

−=−−=+−= xxxxx

Здесь

х

1

, х

2

, х

4

― базисные переменные, х

3

― свободная пере-

менная, которая может принимать любые действительные зна-

чения. Решение может быть записано в виде

. ,1;;

7

5

7

5

;

7

3

7

11

Rccccx

T

∈

⎟

⎠

⎞

⎜

⎝

⎛

−−−+−=

Пример 5. Найти фундаментальную систему решений

однородной системы уравнений:

⎪

⎩

⎪

⎨

⎧

=+−+−

=+−

=+−++

=+−+−

.05274

,0 5

,07245

,04223

54321

521

54321

xxxxx

xxx

xxxxx

Решение.

~

0

51274

72415

41223

10051

~

0

51274

10051

72415

41223

⎟

⎠

⎞

⎜

⎝

⎛

−−

−

−−

−

⎟

⎠

⎞

⎜

⎝

⎛

−−

−

−−

29 30

.

0

00000

112130

10051

~

0

112130

224260

112130

10051

~

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

−

Соответствующая система будет иметь вид:

⎩

⎨

⎧

++=

−=

.213

,5

5524

521

xxxx

xxx

Будем придавать свободным переменным

х

2

, х

3,

х

5

после-

довательно значения 1 (когда две другие переменные равны

нулю). Получим фундаментальную систему решений:

()

).0 ,1 (çäåñü 1 1; 0; 0; ;1

),0 ,1 (çäåñü 0 2; 1; 0; ;0

),0 ,1 (çäåñü 0 13; 0; 1; ;5

, , , ;213 ; ;5

3253

5232

5311

5325532252

===−=

====

∈

++

−

xxxx

Rxxxxxxxxxx

2.2. Задачи для самостоятельного решения

1. Найти решение системы уравнений АХ=В для заданных

матриц А и В:

А В А В

1.1 -2 -1 -6 -3 2 1.11 2 -2 -2 -2 1

-5 3 -5 -1 -5 0 -5 -5 5 -3

-1 -2 2 4 0 -3 -4 0 1 5

-4 2 3 6 -7 -5 -7 -3 8 1

1.2 -6 3 5 5 -2 1.12 1 -2 1 0 -6

3 5 -6 4 4 -6 1 -4 3 -6

-5 3 2 0 5 4 -2 3 -1 -6

4 5 -9 -1 11 -3 1 -2 2 -6

1.3 4 -3 2 -6 3 1.13 0 2 -3 2 -1

-6 -1 -3 1 -6 -4 5 2 0 4

0 2 -6 2 -1 -3 3 0 3 -1

-10 4 -11 9 -10 -7 6 5 1 4

1.4 0 4 -4 -1 -4 1.14 -6 -4 0 0 0

520-61 2-64 5 -5

1 -6 -6 -4 -6 -6 -3 2 1 4

6-8-2-9 -1 2-56 6 -1

1.5 2 1 5 0 2 1.15 -4 4 5 0 5

3 -2 -5 -6 1 2 -1 -5 4 1

3 3 -1 -2 -5 4 -3 -1 -5 -2

40-11-8-6 10-8

-

11 -1 -6

1.6 4 5 0 -2 -4 1.16 -4 2 -3 4 -4

-2 0 1 -3 -2 1 3 -1 0 -4

-5 -5 1 -2 -5 5 4 3 1 2

-11 -10 2 -3 -3 10 5 5 -3 2

1.7 0 -2 2 -4 4 1.17 4 -6 4 3 -4

-5 -6 -2 0 0 -3 3 -2 -1 4

1 2 -5 -5 -4 5 -3 0 0 -4

-4 -2 -9 -1 -8 -2 6 -6 -4 4

1.8 0 -3 4 2 -2 1.18 5 2 0 -3 4

-6 -2 -3 0 -4 2 -3 0 -4 -6

-5 -5 0 -2 -1 -3 -1 -4 -6 0

-11 -4 -7 -4 -3 -6 -6 -4 -7 -10

1.9 1 -6 2 1 -5 1.19 -6 0 -3 -3 -5

1 0 1 2 -2 1 -2 0 -3 -5

0 -1 -2 -5 -4 3 1 -2 -4 -5

0 5 -3 -4 -1 10 -1 1 -4 -5

1.10 -1 5 5 -4 -4 1.20 -1 2 -5 5 5

-2 -1 -6 -3 2 2 -2 -2 -2 1

-5 3 -5 -1 -5 0 -5 -5 5 -3

-1 -2 2 4 0 -3 -4 0 1 5

31 32

2. Найти фундаментальную систему решений однородной

системы уравнений

АХ=0 для заданной матрицы А:

А А

2.1 2 -1 5 -5 2.11 5 0 -4 -4

2 -1 0 -4 -6 5 -4 5

-3 452 2014

-3 4 0 3 -9 5 1 13

2.2 -4 4 -2 0 2.12 -2 3 3 2

-4 5 -3 3 -2 -4 -2 0

-1 -3 1 4 2 0 5 -1

-1 -2 0 7 2 -7 0 -3

2.3 4 -1 -1 -2 2.13 -3 -1 0 5

2 0-1-4 1 25 -1

0 -6 5 0 -6 -5 0 1

-2 -5 5 -2 -2 -2 5 -5

2.4 2 -3 0 -5 2.14 5 -1 -4 -2

3 053 3 4-6 3

5 152 2-42-6

6 4 10 10 0 1 0 -1

2.5 5 4 1 -1 2.15 2 0 4 4

-6 4 -6 3 3 -2 -3 3

-3 4 0 -5 4 -4 2 0

-14 4 -7 -1 5 -6 -5 -1

2.6 4 -2 -2 5 2.16 -4 -5 4 -5

2 -1 -3 -4 4 -6 -5 4

-2 -6 5 5 3 5 -1 5

-4 -5 4 -4 11 4

-

10 14

2.7 4 3 0 -1 2.17 0 0 -2 -6

-6 -1 3 -5 -3 -3 2 -4

-5 -3 -6 1 5 -5 -6 1

-15 -7 -3 -3 2 -8 -2 3

2.8 2 -6 -3 4 2.18 4 2 1 4

1 3 5 2 -5 -4 1 1

-2 3-6-6 5 -50 -2

-3 12 2 -8 -4 -11 0 -5

2.9 0 -1 5 -6 2.19 -3 5 4 5

-2 4 4 -6 -4 -1 1 -2

3 -2 4 4 0 4 -1 -5

1 3 3 4 -1 -2 -4 -12

2.10 0 -4 -1 0 2.20 -3 -6 2 1

5 1 1 3 -4 -4 -4 2

4 2 -5 -6 -6 1 4 2

9 7 -3 -3 -7 3 -2 3

3. СОБСТВЕННЫЕ ВЕКТОРЫ И СОБСТВЕННЫЕ

ЗНАЧЕНИЯ

Пусть А – квадратная матрица порядка n и

.

...

2

1

⎟

⎠

⎞

⎜

⎝

⎛

=

n

x

Чис-

ло

λ называется собственным значением матрицы А, если су-

ществует ненулевой вектор

x , такой, что выполняется равен-

ство

.xxA

λ

=

Вектор x , удовлетворяющий последнему равенству, называет-

ся собственным вектором матрицы

А, соответствующим с соб-

ственному значению

λ.

Справедливы следующие свойства:

1.

собственный вектор матрицы имеет единственное собст-

венное значение;

2.

собственный вектор матрицы А, соответствующий собст-

венному значению

λ, определяется с точностью до постоянного

множителя;

33 34

3. если

1

x и

2

x линейно независимые собственные векторы

матрицы А с одним и тем же собственным значением

λ, то

1

x

+

2

x

― тоже собственный вектор матрицы А с собственным

значением

λ;

4.

собственные векторы матрицы А, соответствующие по-

парно различным собственным значениям, линейно независи-

мы;

Изучим задачу нахождения собственных векторов и собствен-

ных значений матрицы. Преобразуем равенство

xxA

λ

= :

,0)(00 =−→=−→=−→= xEAxExAxxAxxA

λλλλ

где Е ― это соответствующая единичная матрица. Последнее

равенство в развернутом виде представляет собой однородную

систему n линейных уравнений с n неизвестными:

(

)

()

⎪

⎩

⎪

⎨

⎧

=−+++

=++−+

=+++−

.0...

...................................................

,0...

2211

2222121

1212111

nnnnn

nn

xaxaxa

λ

Однородная система имеет ненулевое решение тогда и

только тогда, когда ее определитель равен нулю:

()

.0

...

............

...

det

21

22221

11211

=

−

=−

λ

nnnn

n

aaa

EA

Уравнение

0=− EA

λ

называется характеристическим

уравнением матрицы А. Его корни ― характеристические чис-

ла или собственные значения матрицы А.

3.1. Примеры решения типовых задач

Пример. Найти собственные значения и собственные век-

торы матрицы

.

18

21

⎟

⎠

⎞

⎜

⎝

⎛

=

A

Решение. Характеристическое уравнение для данной мат-

рицы будет иметь вид:

() ()

.0161

18

21

det

2

=−−=

−

=−

λ

EA

Его корни:

.5 ,3

21

=

−

=

λ

Для

3

1

−

=

λ

составим систему вида

(

)

0

1

=− xEA

λ

:

.02

048

,024

21

=+

⎩

⎨

⎧

⇔

=+

xx

Уравнения системы пропорциональны. Система имеет

ненулевое решение

Rxx

∈

−

=

112

x,2 ― свободная переменная.

Таким образом, собственному значению

3

1

−

=

λ

соответ-

ствует собственный вектор

(

)

. ,2,

111

Rxxx

∈

Для

5

2

=

λ

соответствующая система будет иметь вид:

.02

048

,024

21

=+−

⎩

⎨

⎧

⇔

=−

=+−

xx

Решение системы

Rxx

∈

=

112

x,2 ― свободная переменная.

Следовательно, собственному значению

5

2

=

λ

соответ-

ствует собственный вектор

(

)

. ,2,

111

Rxxx

∈

3.2. Задачи для самостоятельного решения

Найти собственные значения и собственные векторы мат-

риц:

35 36

1.

;

100

111

020

⎟

⎠

⎞

⎜

⎝

⎛

2.

;

080

110

1101

⎟

⎠

⎞

⎜

⎝

⎛

−

3.

;

110

211

222

⎟

⎠

⎞

⎜

⎝

⎛

−

−−−

4.

;

113

151

311

⎟

⎠

⎞

⎜

⎝

⎛

5.

;

011

223

001

⎟

⎠

⎞

⎜

⎝

⎛

−

6.

;

033

303

330

⎟

⎠

⎞

⎜

⎝

⎛

7.

;

122

212

221

⎟

⎠

⎞

⎜

⎝

⎛

8.

;

000

030

002

⎟

⎠

⎞

⎜

⎝

⎛

−

9.

;

131

111

322

⎟

⎠

⎞

⎜

⎝

⎛

−

10.

;

100

121

112

⎟

⎠

⎞

⎜

⎝

⎛

11.

;

111

212

214

⎟

⎠

⎞

⎜

⎝

⎛

−

−−

12. ;

148

474

841

⎟

⎠

⎞

⎜

⎝

⎛

−−

−

13. ;

6121

131

4123

⎟

⎠

⎞

⎜

⎝

⎛

−

−−−

−

14.

;

200

010

101

⎟

⎠

⎞

⎜

⎝

⎛

15

.

022

231

213

⎟

⎠

⎞

⎜

⎝

⎛

−

4. ОСЬ И ОТРЕЗОК ОСИ.

КООРДИНАТЫ НА ПРЯМОЙ

Определение. Прямая, на которой выбрано положитель-

ное направление, называется

осью.

Отрезок оси, ограниченный какими-нибудь точками

А и

В, называется направленным, если указано, какая из этих то-

чек является началом отрезка, а какая ― концом.

Направленный отрезок с началом в точке

А и концом в

точке

В обозначается

A

B

. Пусть выбрана единица масштаба.

Величиной направленного отрезка оси называется его длина,

взятая со знаком плюс, если направление отрезка совпадает с

положительным направлением оси, и со знаком минус, если

это направление противоположно положительному направле-

нию оси.

Величина отрезка AB обозначается символом АВ,

его длина ― символом

|АВ|.

Определение. Пусть дана произвольная прямая а. Выбе-

рем некоторый отрезок в качестве единицы измерения длины;

выберем на прямой

а положительное направление и произ-

вольную точку

О. Тогда на прямой а будет введена система

координат (рис. 2).

Рисунок 2

Определение. Пусть на прямой а задана система ко-

ординат. Координатой любой точки

М на прямой называется

число

х, равное величине отрезка ОМ: х=ОМ.

Точка

О называется началом координат, и ее собственная

координата равна нулю. Символом

М(х) будем обозначать тот

факт, что точка

М имеет координату х.

Пусть

)(

11

xM

и

)(

22

xM

― две произвольные точки на

оси

а. Тогда формула

М

1

М

2

= х

2

- х

1

выражает величину отрезка М

1

М

2

, а

формула

1221

xxMM −=

выражает его длину.

Для любых трех точек

А, В, С на оси а справедливо ра-

венство

AB BC AC+=, которое называется основным тож-

деством

.

Число

CB

AC

=

λ

называется отношением, в котором точ-

ка

С делит отрезок АВ. Если 0<

λ

<1, то точка С лежит между

точками

А и В. Пусть даны точки

)(

11

xM

и

)(

22

xM

. Тогда

37 38

координату точки М, делящей отрезок М

1

М

2

в отношении

λ

,

находим по формуле

.

1

21

λ

+

=

хх

х

В частности, середина отрезка

М

1

М

2

(

λ

=1) находится по

формуле

.

2

21

хх

х

+

=

4.1. Примеры решения типовых задач

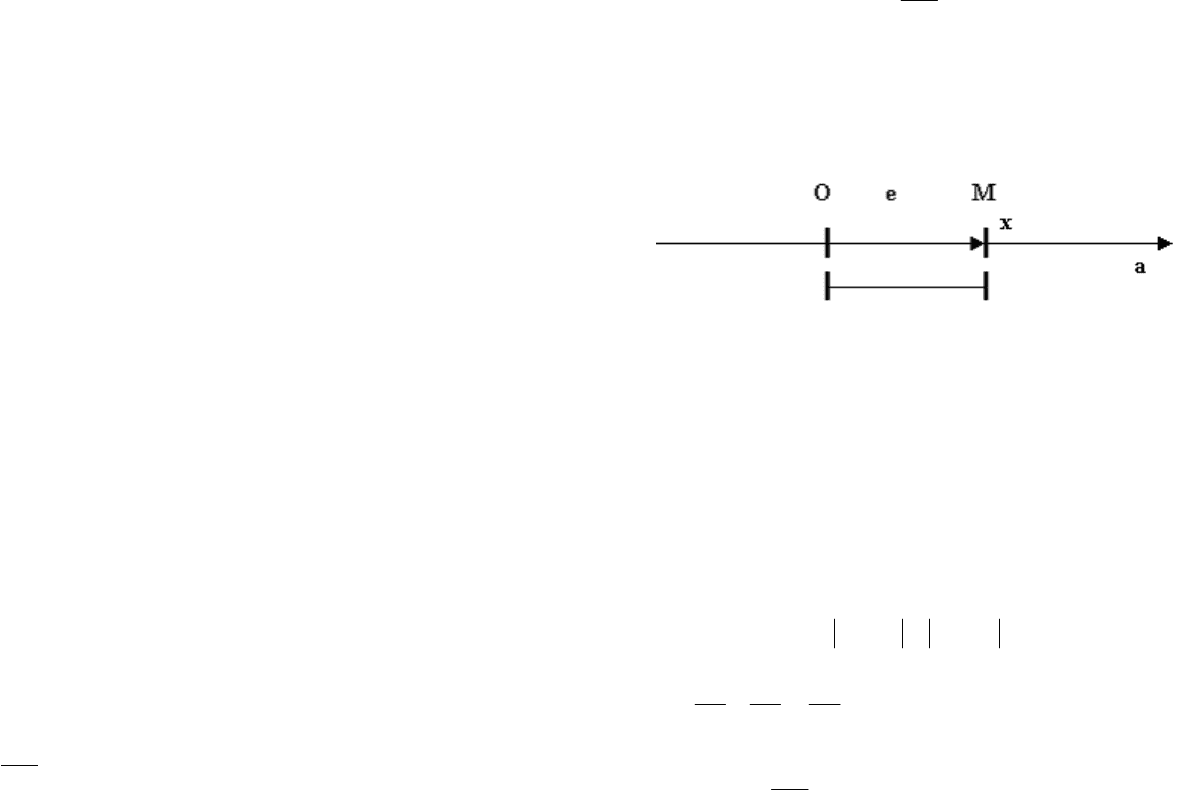
Пример 1. Построить на координатной оси точки А(3),

В(-2), С(5/2), D(

10

).

Решение. Возьмем произвольную прямую l, выберем на-

чало координат

О, положительное направление и единичный

отрезок

ОЕ

Рисунок 3

Отложив три единицы вправо (три отрезка ОЕ) от точки

О, получим точку А. Отложив две единицы влево от точки О,

получим точку

В (рис. 3).

Точка

С (рис. 4) представляет собой середину отрезка

ОХ, равного пяти единичным отрезкам

ОЕ=е.

Рисунок 4

Отрезок ОD равен гипотенузе прямоугольного треуголь-

ника с катетами

а=1 и b=3 (рис. 5).

Рисунок 5

Пример 2. Построить точки, координаты которых удов-

летворяют уравнениям 1) ⏐

х⏐=2; 2) ⏐х-5⏐=2.

Решение. Решая уравнения, находим: 1) х=2; x=-2;

2)

х-5=2, х-5=-2 или х=7; х=3. Далее аналогично примеру 1

строим точки с координатами

А

1

(2); А

2

(-2); А

3

(7); А

4

(3).

Пример 3. Определить величину АВ и длину ⏐АВ⏐ отрез-

39 40

ка, заданного точками А(-5); В(1).

Решение. По формулам АВ=х

2

-х

1

, ⏐АВ⏐=⏐х

2

-х

1

⏐ в каж-

дом случае находим

АВ=1-(-5)=6, ⏐АВ⏐=⏐6⏐=6.

Ответ:

АВ=6; ⏐АВ⏐=6.

Пример 4. Определить координату точки А, если извест-

ны

В(4) и ⏐АВ⏐=5.

Решение. Пусть точка А имеет координату х. Тогда по ус-

ловию ⏐

4-х⏐=5. Решив это уравнение, находим х=-1, х=9.

Ответ: х=-1; х=9.

Пример 5. Определить координату точки М, если извест-

ны

М

1

(2), М

2

(8) и .3

2

1

==

ММ

λ

Решение. Пусть точка М имеет координату М(х). Тогда

по формуле

λ

+

=

1

21

xx

x

находим: х= .5,6

4

26

31

832

==

+

⋅

+

Ответ: 6,5

4.2. Задачи для самостоятельного решения

1. Построить на числовой оси точки А(-5), В(4) и С(-2) и най-

ти величины АВ, ВС и АС. Проверить, что АВ+ВС=АС.

2.

Построить точки, координаты которых удовлетворяют

уравнениям: 1)⏐

х⏐=4; 2) ⏐х-1⏐=8; 3) ⏐1-х⏐=2; 4) ⏐х+2⏐=2.

3.

Определить величину АВ и длину ⏐АВ⏐ отрезка, заданного

точками: 1) А(3) и В(11); 2) А(5) и В(2); 3) А(-1) и В(3); 4) А(-5)

и В(-3); 5) А(-1) и В(-3); 6) А(-7) и В(-5).

4.

Вычислить координату точки А, если известны: 1) В(3) и

ВА=-3; 2) В(2) и АВ=-3; 3) В(-1) и ВА=2; 4) В(-5) и ВА=-3;

5) В(0) и ⏐АВ⏐=2; 6) В(2) и ⏐АВ⏐=3; 7) В(-1) и ⏐АВ⏐=5;

8) В(-5) и ⏐АВ⏐=2.

5.

Определить отношение λ=АС/СВ, в котором точка С делит

отрезок АВ при следующих данных:

1) А(2), В(6) и С(4); 2) А(2), В(4) и С(7); 3) А(-1), В(5) и С(3);

4) А(1), В(13) и С(5); 5) А(5), В(-2) и С(-5).

6.

Определить координату точки М, если известны:

1) М

1

(3), М

2

(7) и λ= М

1

М/ MМ

2

=2; 2) А(2), В(-5) и

λ=АМ/МВ=3;

3) С(-1), D(3) и λ=CМ/МD=1/2; 4) A(-1), B(3) и λ=BМ/МA=-2;

5) A(1), B(-3) и λ=AМ/МB=-3; 6) A(-2), B(-1) и λ=BМ/МA=-1/2.

Пчельник В.К. Пособие по курсу высшая математика. Матрицы и определители

Подождите немного. Документ загружается.