Підручник - Алгебра і початок аналізу 10 клас Нелін Академічний рівень
Подождите немного. Документ загружается.

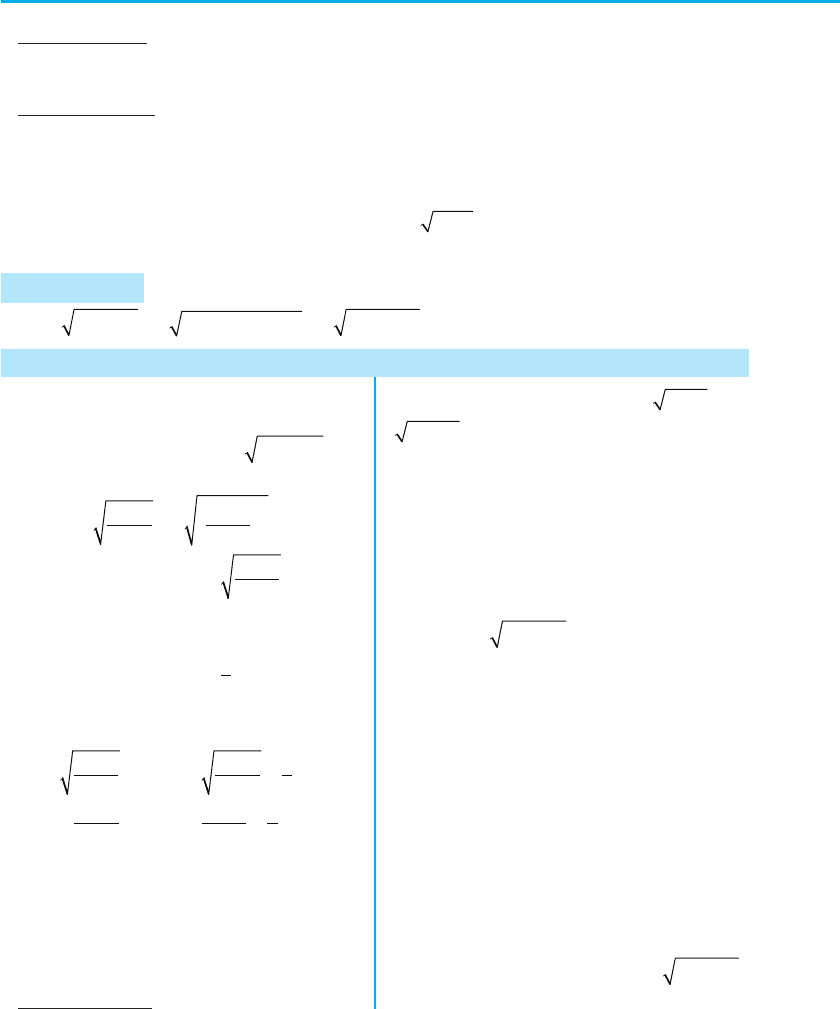
§ 13. Застосування властивостей функцій до розв’язування ірраціональних рівнянь 211
Проміжок ІI. При t ∈ [1; 2] маємо рівняння
–(t – 2) + (t – 1) = t
2
+ 3, яке рівносильне рівнянню t
2
= –2, що не
має коренів. Отже, у проміжку [1; 2] коренів немає.
Проміжок III. При t ∈ [2; +∞) маємо рівняння
(t – 2) + (t – 1) = t
2
+ 3, з якого одержуємо рівняння t
2
– 2t + 6 = 0,
що не має коренів. Отже, у проміжку [2; +∞) коренів немає.
Об’єднуючи одержані результати, робимо висновок, що рівняння (1)
має тільки один корінь t = 0.
Виконуючи обернену заміну, маємо
x −=
10
, звідки x = 1.
Відповідь: 1.
Приклад 3 Розв’яжіть рівняння
() ()
()()
.xx
xx
−− −+++=63 62 3223 0
2
3
3
2
3
Розв’язання Коментар
Оскільки x = 6 не є коренем
заданого рівняння, то при діленні
обох частин рівняння на
x −
()
≠
60
2
3
одержуємо рівносильне рівняння
13
20
23
6
23
6
3
2
3
−+
(
)
=
+
−
+
−
x
x
x
x
.
Після заміни t
x
x
=
+
−
23
6
3
маємо
рівняння 2t
2
– 3t + 1 = 0, корені
якого:
t
1
= 1,
t
2
1
2
= .
Виконав�и обернену заміну,
одержуємо:
23
6
3
1
x
x
+
−
=
або
23
6
1
2
3
x
x
+
−
= ,
23
6
1
x
x
+
−
= або
23
6
1
8
x
x
+
−
= ,
x = –9 або x = –2.
Відповідь: –9; –2.
Виконуємо заміну
xu
−=6
3
,
23
3
xv
+= та одержуємо рівняння
u
2
– 3uv + 2v
2
= 0, усі члени якого
мають однаковий сумарний сте-
пінь
1
— два. Таке рівняння назива-
ють однорідним і розв’язують
діленням обох частин на найвищий
степінь однієї із змінних. Розділимо
обидві частини, наприклад, на u
2
(тобто на
()
.x −
)
6
2
3
Щоб при діленні на вираз із
змінною не загубити корені рівнян-
ня, потрібно ті значення змінної,
при яких цей вираз дорівнює нулю,
розглянути окремо, тобто в цьому
прикладі підставити значення х = 6
в задане рівняння (це можна вико-
нати усно, до розв’язання записати
тільки одержаний результат).
Для того щоб здійснити такий
план розв’язування, не обов’язково
вводити змінні u і v: достатньо помі-
тити, що задане рівняння однорідне,
розділити обидві частини на
()
,x −6
2
3
а вже потім ввести нову змінну t.
1
В означенні однорідного рівняння не враховують член 0, який степеня не має.

212 Розділ 2. СТЕПЕНЕВА ФУНКЦІЯ
Запитання для контролю
1.
Поясніть, які обмеження доведеться накласти на змінну х, щоб розв’язати
рівняння
xx
−=−
26
за допомогою рівносильних перетворень.
2. Наведіть приклад однорідного ірраціонального рівняння. Складіть
план його розв’язування.
Вправи
1. Розв’яжіть ірраціональне рівняння за допомогою рівносильних пе-
ретворень:
1)
325
xx
−=− ;
2)
32
11
−−−=
xx
;
3)
34 42xx x++ −= ;
4)
xxx++
=+54
9.
Розв’яжіть рівняння (2–5).
2. 1)
xx xx x+−+− −=+21 21 1;
2)
xxxx−− −+ −−=32 44
41
.
3. 1) xxx+
()
+−
()
=−
12 13 1
2
3
2
3
2
3
; 2)
xxxx
2
12
10
++−+=().
4. 1) xx xx−− −=
−+
12
32
2
4
; 2) 23 212
33
xx
+− +=.
5. 1)
xx
x
x
x
5
3
5
3
5
5
1
1
1
1
16
−
−
−
−
+=
; 2)
11
1
3
33
xx xx
+−
+=
.
§ 14
ІРРАЦІОНАЛЬНІ НЕРІВНОСТІ
Таблиця 23
Орієнтир Приклад
1. Метод інтервалів (для нерівностей виду f (x)
0)
1) Знайти ОДЗ нерівності.
2) Знайти нулі функції f (x)
(f (x) = 0).
3) Відмітити нулі функції на
ОДЗ і знайти знак функції
в кожному проміжку, на які
розбивається ОДЗ.
4) Записати відповідь, урахо ву-
ючи знак нерівності
Розв’яжіть нерівність
xx
+>+
42
.
Задана нерівність рівносильна нерів-
ності xx+−−>
42
0.
Позначимо
fx
xx
() .=+−−
42
ОДЗ: х + 4 l 0, тобто х l –4.
Нулі f (x):
xx+−−=
42
0,
xx
+=+
42
,
х + 4 = х
2
+ 4х + 4, х
2
+ 3х = 0, х
1
= 0 —
корінь, х
2
= –3 — сторонній корінь.
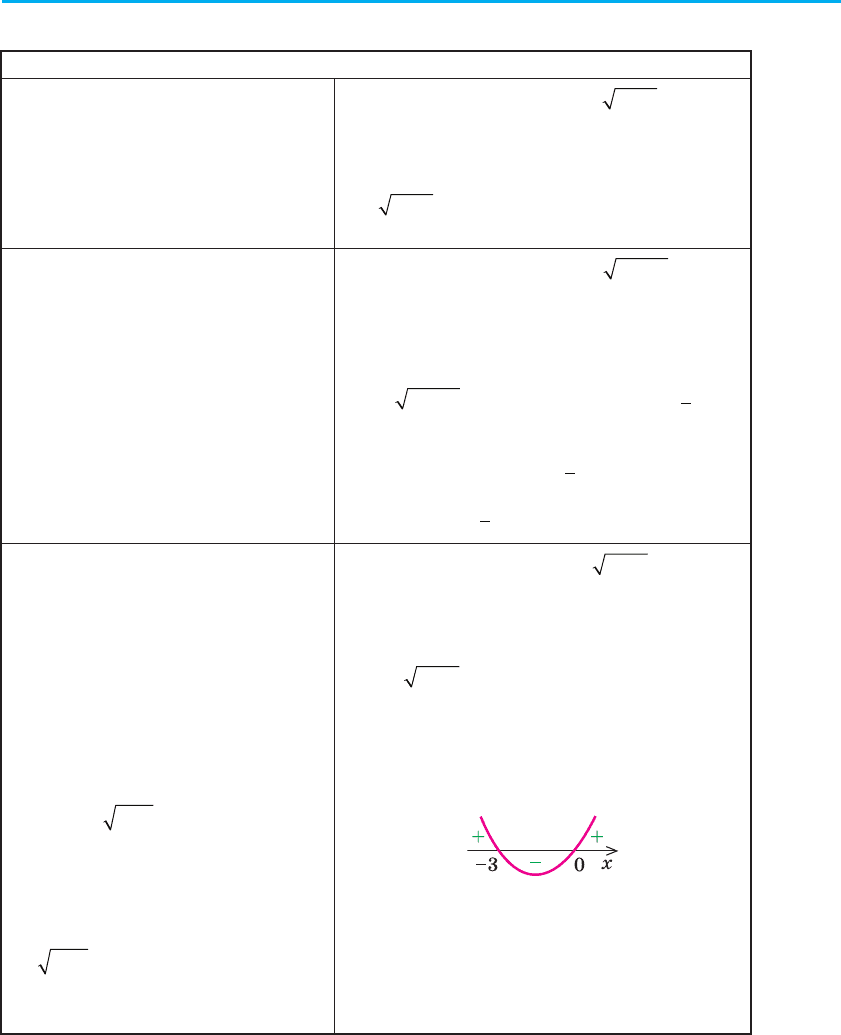
Відмічаємо нулі на ОДЗ і знаходимо знак
функції f (x) у кожному проміжку.
Відповідь: [–4; 0).
§ 14. Ірраціональні нерівності 213
Продовження табл. 23
2. Рівносильні перетворення
1) При піднесенні обох частин
нерівності до непарного сте-
пеня (із збереженням знака
нерівності) одержуємо нерів-
ність, рівносильну заданій
(на ОДЗ заданої)
Розв’яжіть нерівність x +<−
21
3
.
ОДЗ: х ∈ R.
Задана нерівність рівносильна нерівно-
стям:
x +
()
<−
21
3
3
3
()
, х + 2 < –1, х < –3.
Відповідь: (–∞; –3).
2) Якщо обидві частини не-
рівності невід’ємні, то при
піднесенні обох частин не-
рівності до парного степеня
(із збереженням знака нерів-
ності) одержуємо нерівність,
рівносильну заданій (на ОДЗ
заданої)
Розв’яжіть нерівність
261
4
x −<.
ОДЗ: 2х – 6 l 0, тобто х l 3. Обидві
частини заданої нерівності не від’ємні,
отже, вона рівносильна (на її ОДЗ) не-
рівностям:
26 1
4
4
4
x −
()
< , 2х – 6 < 1,
x <
7
2
.
Ураховуючи ОДЗ, одержуємо
3
7
2
m x < .
Відповідь: 3
7
2
;.
)
3) Якщо на ОДЗ заданої не-
рівності якась частина не-
рівності може набувати як
додатних, так і від’ємних
значень, то, перш ніж під-
носити обидві частини не-
рівності до парного степеня,
ці випадки слід розглядати
окремо.
Наприклад,
fx gx
gx
fx gx
k
k
() ()
() ,
() ()
2
2
0
>⇔
>
l
fx gx
gx
fx
gx
k
k
() ()
() ,
() ()
2
2
0
>⇔
>
l
або
fx
gx
() ,
() .
l 0
0<
fx gx
fx
gx
fx
gx
k
k
() ()
() ,
() ,
() ()
2
2
0
0<⇔ >
<
l
Розв’яжіть нерівність
xx
+>+
42
.
Задана нерівність рівносильна сукуп- сукуп-сукуп-
ності систем:
x
xx
+
+
()
>+
20
42
2
2
l ,
()
або
x
x
+
+<
40
20
l ,
.
Тоді
x
xx
l −
+<
2
30
2
,
або
x
x
l −
<−
4
2
,
.
Розв’язав�и нерівність х
2
+ 3х < 0, ма-
ємо –3 < х < 0.
Ураховуючи нерівність х l –2, одер-
жуємо розв’язок пер�ої системи:
–2 m х < 0. Розв’язок другої системи:
–4 m х < –2. Об’єднуючи ці розв’язки,
одержуємо відповідь.
Відповідь: [–4; 0).

214 Розділ 2. СТЕПЕНЕВА ФУНКЦІЯ
Пояснення й обґрунтування
1. Розв’язування ірраціональних нерівностей методом інтервалів.
За галь ну схему розв’язування нерівностей методом інтервалів по-
яснено в § 4 розділу 1, а приклад застосування методу інтервалів до
розв’язування ірраціональних нерівностей наведено в таблиці 23.
2. Рівносильні перетворення ірраціональних нерівностей. Коли для
розв’язування ірраціональних нерівностей використовують рівносильні
перетворення, то найчасті�е за допомогою піднесення обох частин нерів-
ності до одного й того самого степеня задана нерівність зводиться до раціо-
нальної нерівності. При цьому потрібно мати на увазі такі властивості.
1) Якщо обидві частини нерівності доводиться підносити до непар-
ного степеня, то скористаємося тим, що числові нерівності A > B
і A
2k + 1
> B
2k + 1
або одночасно правильні, або одночасно неправильні.
Тоді кожен розв’язок нерівності
f (x) > g (x) (1)
(який перетворює цю нерівність у правильну числову нерівність)
буде також і розв’язком нерівності
f
2k + 1
(x) > g
2k + 1
(x) (2)
і, навпаки, кожен розв’язок нерівності (2) буде також і розв’язком
нерівності (1), тобто нерівності (1) і (2) — рівносильні. Отже, при
піднесенні обох частин нерівності до непарного степеня (із збере-
женням знака нерівності) одержуємо нерівність, рівносильну зада-
ній (на ОДЗ заданої).
Наприклад,
fx gx fx
gx
k
k
() () () ()
21
21
+
+
>⇔>
2) Аналогічно, якщо числа A і B невід’ємні (A l 0, B l 0), то число-
ві нерівності A > B і A
2k
> B
2k
також або одночасно правильні, або
одночасно неправильні. Повторюючи попередні міркування, маємо:
якщо обидві частини нерівності невід’ємні, то при піднесенні обох
частин нерівності до парного степеня (із збереженням знака нерів-
ності) одержуємо нерівність, рівносильну заданій (на ОДЗ заданої).
Наприклад, розглядаючи нерівність
fx gx
k
() ()
2
<
(3)
на її ОДЗ, де f (x) l 0, помічаємо, що для всіх розв’язків нерівно-
сті (3) ліва частина невід’ємна (арифметичний корінь
fx
k
()
2
0l
)
і нерівність (3) може виконуватися тільки за умови
g (x) > 0. (4)
Якщо виконується умова (4), то обидві частини нерівності (3)
невід’ємні, і при піднесенні до парного степеня 2k одержуємо нерівність,
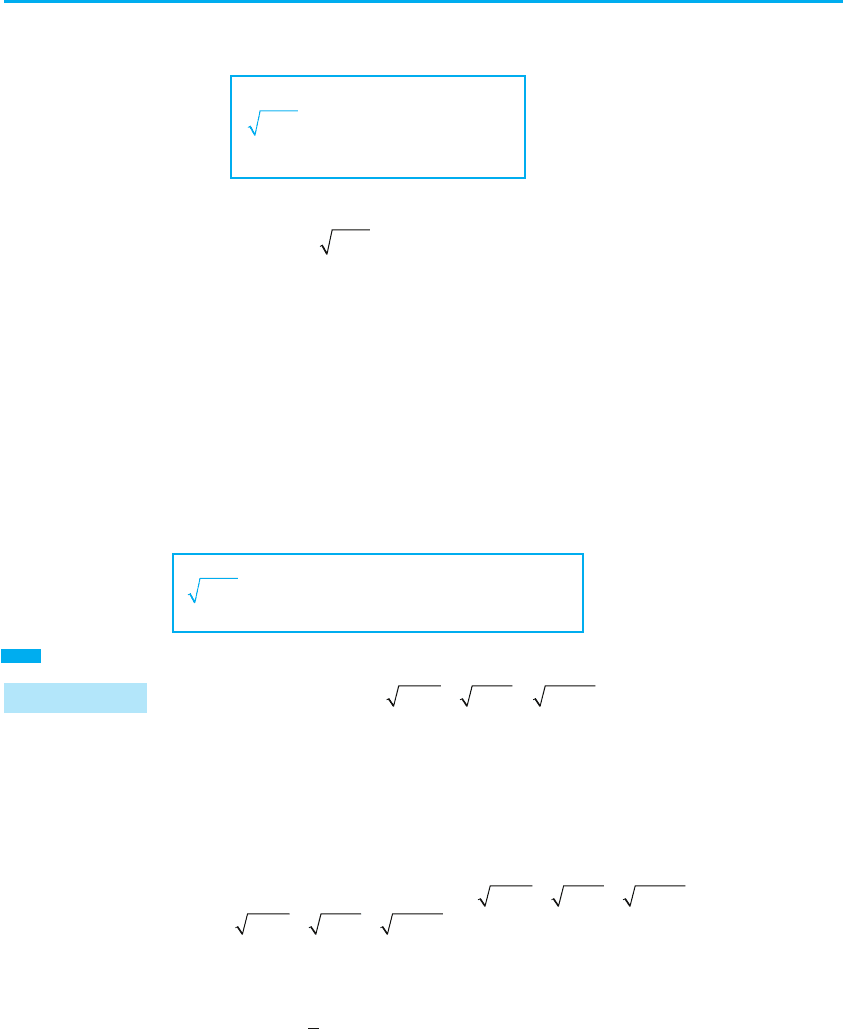
§ 14. Ірраціональні нерівності 215
рівносильну заданій: f (x) < g
2k
(x) (звичайно, за умови врахування ОДЗ
заданої нерівності та умови (4)). Отже,
fx gx
fx
gx
fx
gx
k
k
() ()
() ,
() ,
() ()
2
2
0
0<⇔ >
<
l
3) Якщо за допомогою рівносильних перетворень необхідно розв’язати
нерівність
fx gx
k
() ()
2
>
(5)
на її ОДЗ, де f (x) l 0, то для правої частини цієї нерівності розгля-
немо два випадки: а) g (x) < 0; б) g (x) l 0.
а) При g (x) < 0 нерівність (5) виконується для всіх х з ОДЗ заданої
нерівності, тобто при f (x) l 0.
б) При g (x) l 0 обидві частини нерівності (5) невід’ємні, і при під-
несенні до парного степеня 2k одержуємо нерівність, рівносильну
заданій:
f (x) > g
2k
(x). (6)
Зауважимо, що для всіх розв’язків нерівності (6) обмеження ОДЗ за-
даної нерівності f (x) l 0 виконується автоматично; отже, при g (x) l 0
достатньо записати тільки нерівність (6).
Об’єднуючи одержані результати, доходимо висновку, що:
fx gx
gx
fx gx
fx
gx
k
k
() ()
() ,
() ()
() ,
()
2
2
0
0
0
>⇔
>
<
l
l
або
Приклади розв’язання завдань
Приклад 1 Розв’яжіть нерівність xx x+− −> −31
21
.
Коментар
Зведемо нерівність до виду f (x) > 0 і розв’яжемо її методом інтер-
валів.
Для того щоб знайти нулі функції f (x), використаємо рівняння-
наслідки. Щоб вилучити сторонні корені, виконаємо перевірку одержа-
них розв’язків.
Розв’язання
Задана нерівність рівносильна нерівності xx x+− −− −>31210.
Позначимо fx xx x() .=+−−
−−
31
21
1. ОДЗ:
x
x
x
+
−
−
30
10
210
l
l
l
,
,
.
Тоді
x
x
x
l
l
l
−
3
1
1
2
,
,
,
тобто х l 1.
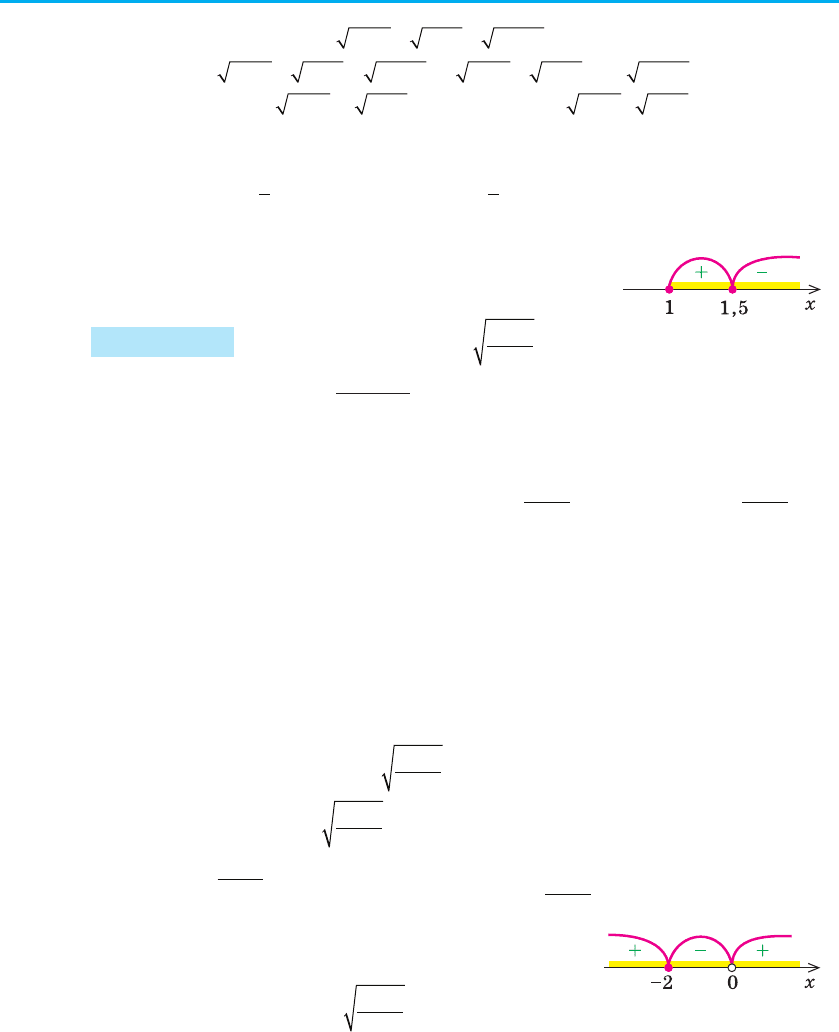
216 Розділ 2. СТЕПЕНЕВА ФУНКЦІЯ
2. Нулі функції f (x):
xx x+− −− −=31210.
Тоді:
xx x+− −= −31
21
,
xx x+− −
()
=−
()
3121
22
,
xxxx x+− +−+−
=−
32 3112 1æ ,
23
13
xx
+−
=
i
.
Підносимо обидві частини останнього рівняння до квадрата:
4 (х + 3) (х – 1) = 9, 4х
2
+ 8х – 21 = 0,
x
1
3
2
15==, — корінь, x
2
7
2
=− — сторонній корінь.
3. Розбиваємо ОДЗ точкою 1,5 на два проміжки і знаходимо знак f (x)
у кожному з проміжків (рис. 97).
Відповідь: [1; 1,5).
Приклад 2 Розв’яжіть нерівність
x
x
x
3
8
2
+
>−.
I спосіб (метод інтервалів)
Коментар
Зведемо задану нерівність до виду f (x) > 0 і розв’яжемо її методом
інтервалів. Для того щоб знайти ОДЗ заданої нерівності, теж застосуємо
метод інтервалів, розв’язуючи нерівність
x
x
3
8
0
+
l (ОДЗ: х ≠ 0;
x
x
3
8
0
+
=
при х = –2).
Для знаходження нулів функції f (x) використаємо рівняння-
наслідки.
Хоча функція f (x) не має нулів, але й у цьому випадку метод інтер-
валів також працює. Тільки інтервали знакосталості функції f (x) збіга-
ються з інтервалами, з яких складається її область визначення.
Розв’язання
Задана нерівність рівносильна нерівності
x
x
x
3
8
20
+
−+> .
(1)
Позначимо fx x
x
x
() .
=−
+
+
3
8
2
1. ОДЗ:
x
x
x
3
8
0
0
+
≠
l ,
.
Розв’яжемо нерівність
x
x
3
8
0
+
l
методом інтервалів (рис. 98).
Одержуємо: х ∈ (–∞; –2] È (0; +∞).
2. Нулі функції f (x):
x
x
x
3
8
20
+
−+= .
Тоді:
Рис. 97
Рис. 98
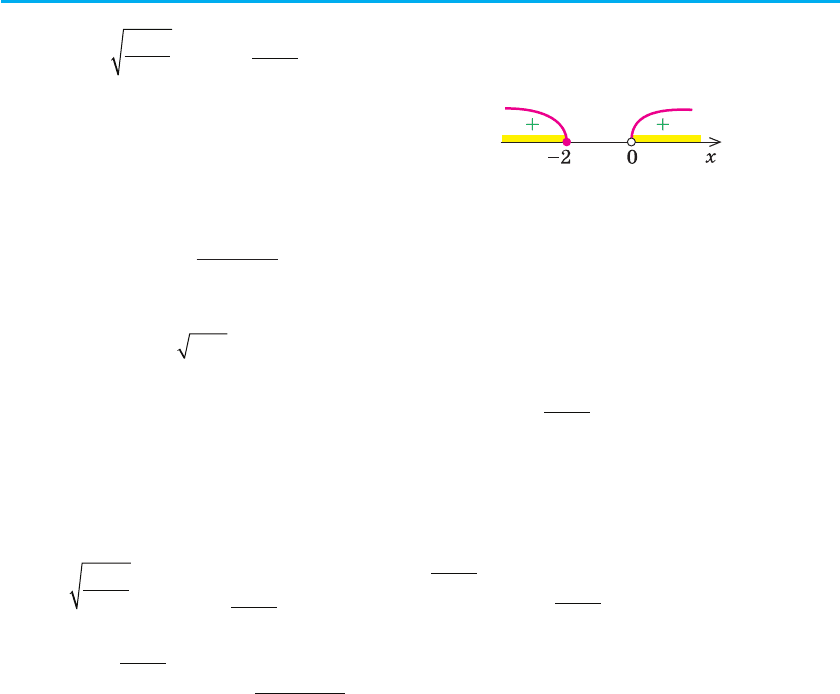
§ 14. Ірраціональні нерівності 217
x
x
x
3
8
2
+
=−,
x
x
xx
3
2
8
44
+
=−+ , х
3
+ 8 = х
3
– 4х
2
+ 4х,
4х
2
– 4х + 8 = 0 — коренів немає (D < 0).
3. ОДЗ нерівності (1) розбивається на два
проміжки, у яких функція f (x) має зна-
ки, указані на рисунку 99.
Відповідь: (–∞; –2] È (0; +∞).
ІІ спосіб (рівносильні перетворення)
Коментар
Для розв’язування використаємо рівносильні перетворення:
fx gx
gx
fx
gx
k
k
() ()
() ,
() ()
2
2
0
>⇔
>
l
або
fx
gx
() ,
() .
l 0
0<
Щоб розв’язати одержану проміжну нерівність
x
x
3
8
0
+
l , урахуємо
умови, за яких цей дріб буде невід’ємним.
У кінці, об’єднуючи одержані розв’язки, отримуємо відповідь.
Розв’язання
x
x
x
x
x
x
x
3
3
2
8
8
2
20
2
+
+
>−⇔
−
>−
l ,
()
,
або
x
x
x
x
x
x
xx
3
3
2
8
8
0
20
2
44
+
+
−<
⇔
>−+
l
l
,
,
,
або
x
x
x
3
8
0
2
+
<
⇔
l ,
⇔
>
−+
x
xx
x
l 2
0
448
2
,
,
або
x
x
x
3
80
0
2
+
>
<
l
,
,
або
x
x
x
3
80
0
2
+
<
<
m ,
,
.
Ураховуючи, що 4х
2
– 4х + 8 > 0 при всіх значеннях х (D < 0
і а = 4 > 0), одержуємо, що остання сукупність трьох систем рівносильна
сукупності:
x
x
l 2
0
,
>
або
x
x
x
l −
>
<
2
0
2
,
,
,
або
x
x
x
m −
<
<
2
0
2
,
, ⇔
⇔ х l 2, або 0 < x < 2, або х m –2 ⇔ х m –2, або х > 0.
Відповідь: (–∞; –2] È (0; +∞).
Заува ження. Записуючи наведене розв’язання, знаки рівносиль-
ності (⇔) можна не ставити, достатньо на початку розв’язання записати:
«Виконаємо рівносильні перетворення заданої нерівності».
Рис. 99
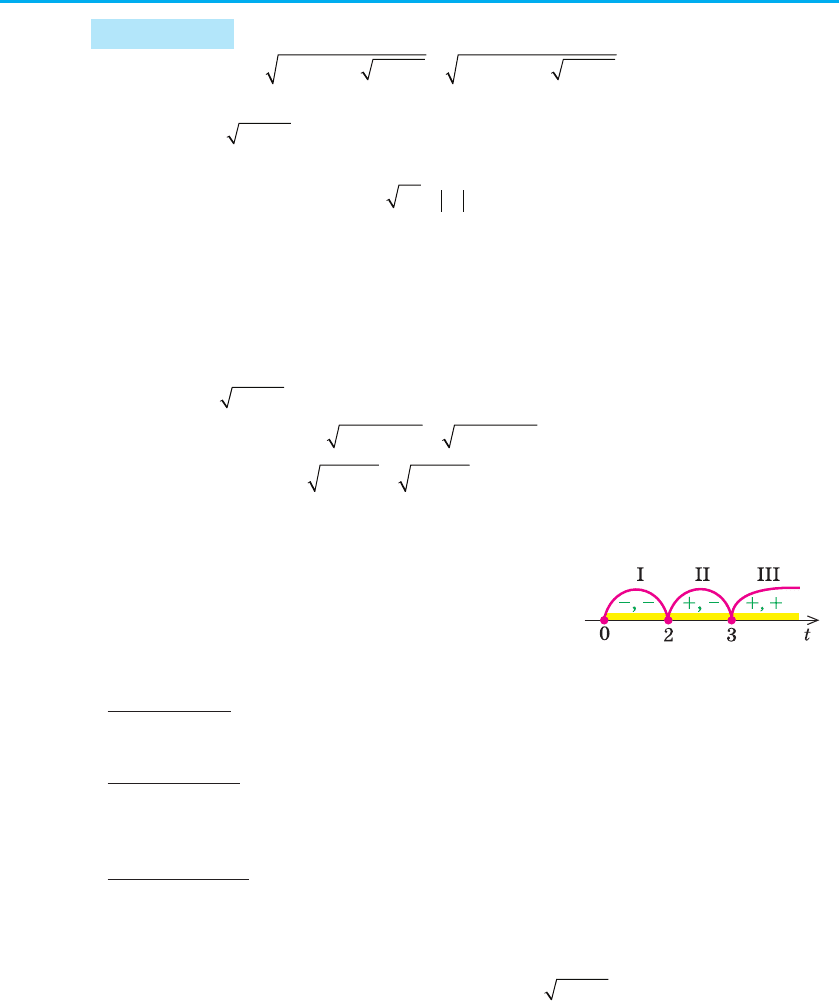
218 Розділ 2. СТЕПЕНЕВА ФУНКЦІЯ
Приклад 3. Розв’яжіть нерівність
3943 5314 63
51
xx
xx
+− ++ +− + m .
(1)
Коментар
Заміна 35
xt+=
дозволяє помітити, що кожен вираз, який стоїть
під знаком зовні�нього квадратного кореня, є квадратом двочлена.
Застосовуючи формулу
aa
2
= , одержуємо нерівність, що містить
знак модуля, для розв’язування якої використовуємо такий план:
1) знайти ОДЗ;
2) знайти нулі всіх підмодульних функцій;
3) відмітити нулі на ОДЗ і розбити ОДЗ на проміжки;
4) знайти розв’язки нерівності в кожному з проміжків.
Розв’язання
Нехай 35
xt
+=, де t l 0. Тоді 3x + 5 = t
2
, 3x = t
2
– 5.
Отримуємо нерівність tt
tt
22
44 96 1+− ++− m , яку можна записати так:
() () .tt−+−
23
1
22
m
Одержуємо
| t – 2 | + | t – 3 | m 1. (2)
1. ОДЗ нерівності (2): t ∈ R, але за змістом завдання цю нерівність по-
трібно розв’язати при t l 0.
2. Нулі підмодульних функцій: t = 2 і t = 3.
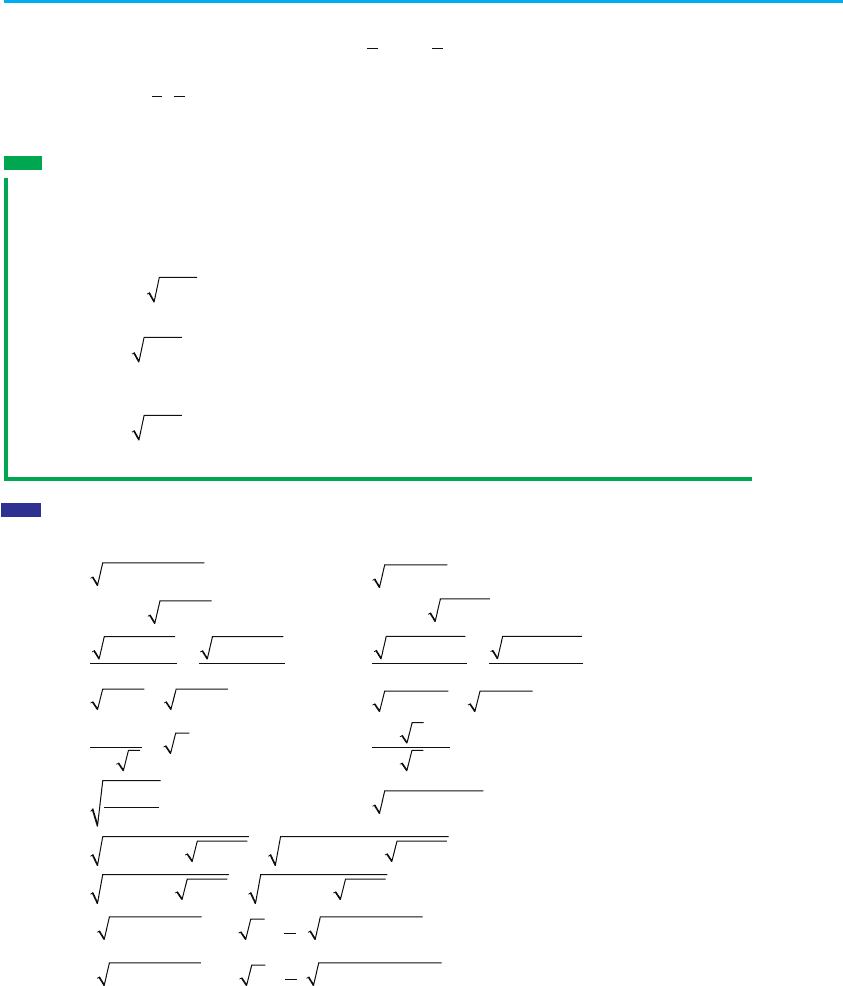
3. Ці нулі розбивають область t l 0 на три
проміжки, у кожному з яких кожна під-
модульна функція має постійний знак
(рис. 100).
Проміжок І. При t ∈ [0; 2] маємо нерівність
–(t – 2) – (t – 3) m 1, з якої одержуємо t l 2, але в проміжок [0; 2]
входить тільки t = 2.
Проміжок ІI. При t ∈ [2; 3] маємо нерівність (t – 2) – (t – 3) m 1, яка
рівносильна нерівності 0•t m 0, що виконується при будь-яких зна-
ченнях t. Отже, у проміжку [2; 3] розв’язками нерівності будуть усі
значення t із цього проміжку (2 m t m 3).
Проміжок III. При t ∈ [3; +∞) маємо нерівність (t – 2) + (t – 3) m 1,
з якої одержуємо t m 3, але в проміжок [3; +∞) входить тільки зна-
чення t = 3.
Об’єднуючи одержані результати, робимо висновок, що розв’язками
нерівності (2) будуть усі значення t такі, що 2 m t m 3.
Виконуючи обернену заміну, маємо 23
53
mm
x + , звідки
4 m 3x + 5 m 9.
Рис. 100
§ 14. Ірраціональні нерівності 219
Тоді −
1
3
4
3
mmx .
Відповідь:
−
1
3
4
3
;.
Запитання для контролю
1. Назвіть основні методи розв’язування ірраціональних нерівностей.
2. Назвіть основні етапи розв’язування ірраціональної нерівності ме-
тодом інтервалів.
3. Обґрунтуйте справедливість таких рівносильних перетворень:
1)
fx gx fx
gx
k
k
() () () ();
21
21
+
+
>⇔>
2)
fx gx
fx
gx
fx
gx
k
k
() ()
() ,
() ,
() ();
2
2
0
0<⇔ >
<
l
3) fx gx
gx
fx
gx
k
k
() ()
() ,
() ()
2
2
0
>⇔
>
l
або
fx
gx
() ,
() .
l 0
0<
Вправи
Розв’яжіть нерівність (1–8).
1. 1)
xx x
2
3184−−<−; 2)
xx x
2
35−<− .
2. 1) xx x−
()
+−
349
22
m ; 2)
xx x−
()
+−
111
22
m .
3. 1)
6
25
6
4
22
+−
+
+−
+
xx
x
xx
x
m ;
2)
32
8
32
21
22
−−
+
−−
+
xx
x
xx
x
m .
4. 1) xx−+ +22
53
l ; 2)
22
0155
xx−++ l .
5. 1)
14
3
5
−
+
x
xl ; 2)
xx
xx
−−
−−
>
2
6
0.
6. 1)
x
x
x
3
27
3
+
>−;
2)
xx x
42
211−+>−.
7
*
. 1) 5865 1524 10 512xx
xx
+− −+ +− − m ;
2) xx
xx
+− −+ +− −>34 18
61
1.
8
*
. 1)
xx xxx
x
22
431826
10
1
−++
()
+−−+
()
m ;
2)
xx xxx
x
22
562102 12
20
1
−++
()
−−−+
()
l .

220 Розділ 2. СТЕПЕНЕВА ФУНКЦІЯ
§ 15
РОЗВ’ЯЗУВАННЯ ІРРАЦІОНАЛЬНИХ РІВНЯНЬ
ТА НЕРІВНОСТЕЙ З ПАРАМЕТРАМИ
При розв’язуванні завдань з параметрами, у яких вимагається роз-
в’язати рівняння чи нерівність, можна користуватися таким орієнтиром
(§ 9): будь-яке рівняння чи нерівність з параметрами розв’язують як
звичайні рівняння чи нерівність доти, поки всі перетворення або мір-
кування, необхідні для розв’язування, можна виконати однозначно. Але
в тому разі, коли якесь перетворення не можна виконати однозначно,
розв’язування необхідно розбити на декілька випадків, щоб у кожному
з них відповідь через параметри записувалася однозначно.
Також на етапі по�уку плану розв’язування рівнянь чи нерівно-
стей з параметрами або міркуючи над самим розв’язанням, часто буває
зручно супроводжувати відповідні міркування схемами, за якими легко
простежити, у який саме момент ми не змогли однозначно виконати по-
трібні перетворення, на скільки випадків довелося розбити розв’язання
і чим відрізняється один випадок від ін�ого.
Зазначимо, що рівняння та нерівності з параметрами найчасті�е
розв’язують за допомогою їх рівносильних перетворень, хоча інколи ви-
користовують і властивості функцій, метод інтервалів для розв’язування
нерівностей та рівняння-наслідки.
Приклад 1 Розв’яжіть рівняння
xa
−=
2.
Коментар
Ми не можемо однозначно дати відповідь на запитання, чи є в за-
даного рівняння корені, і тому вже на пер�ому кроці повинні роз-
бити розв’язання на два випадки:
1) a < 0 — коренів немає, 2) a l 0 —
корені є (див. схему).
При a l 0 маємо найпрості�е ір-
раціональне рівняння, обидві частини
якого невід’ємні. Отже, при піднесенні
до квадрата обох його частин одержу-
ємо рівняння, рівносильне заданому.
ОДЗ заданого рівняння можна не за-
писувати, її враховано автоматично, бо для всіх коренів одержаного рів-
няння x – 2 = a
2
l 0.
Розв’язання
1) При a < 0 рівняння не має коренів.
2) При a l 0 x – 2 = a
2
. Тоді х = а
2
+ 2.
Відповідь: 1) якщо a < 0, то коренів немає;
2) якщо a l 0, то х = а
2
+ 2.
a < 0 a O 0
x – 2 = a
2
коренів немає
х = а
2
+ 2
2xa
−=
