Peube J-L. Fundamentals of fluid mechanics and transport phenomena

Подождите немного. Документ загружается.

442 Fundamentals of Fluid Mechanics and Transport Phenomena

-1 +1

: g

-1

S S S SS S S

: 2P/

: tan









(a) (b)

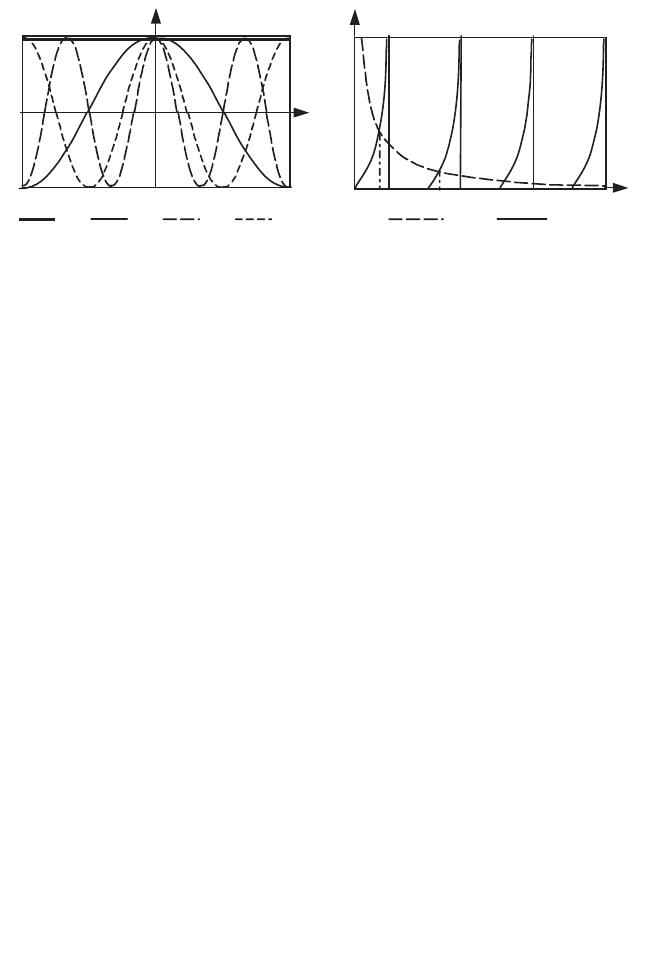
Figure 8.15.

(a) Even eigenfunctions of two walls separate by a thermal resistance;

(b) graphical solution of the eigenvalue equation in the case of odd eigenfunctions

2) Odd eigenfunctions. Substituting the values [8.51] of the pairs (B

–

, B

) into

first relation [8.52], we obtain a second group of solutions

(0, 0):



or BB;AA BB;AA

  

   

We derive the relation:



 BABA cos.cos.

Substituting this expression into [8.52], and taking account of [8.51], we obtain

the eigenvalue equation:

P2tan // [8.54]

whose graphical solution is shown in Figure 8.15b. The eigenfunctions



12 

which correspond to these eigenvalues are here odd and by taking

1 



they present a discontinuity amplitude equal to

cos2



at the origin. They can

be written:



cos)

(:10

121212

/ d



xAxgx

kkk

These discontinuous eigenfunctions depend on the dimensionless parameter P.

We have represented, in Figure 8.16b, the first four odd eigenfunctions

corresponding to

05.0 P

(eigenvalues /

=0.3111, /

=3.1731, /

=6.2991,

/

=9.43538).

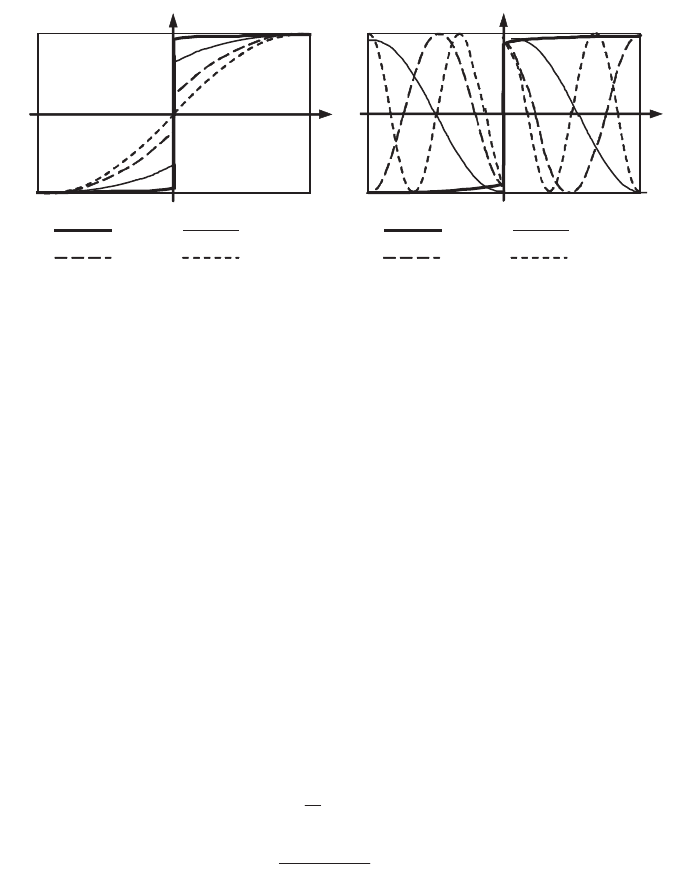
Thermal Systems and Models 443

P =0.05 P =0.5

: g

P =3

P = f

(a) Variations of the eigenfunction

for different values of P.

(b) Discontinuous eigenvalues for

P = 0.05.

+1+1

–

Figure 8.16.

Odd eigenvalues for two walls separated by a thermal resistance

8.3.2.3.3.

Evolution of odd eigenfunctions

The value of thermal resistance placed between the two walls (in other words the

value of P) has a strong influence on the discontinuity amplitude. Figure 8.16a

shows the evolution of the first odd eigenfunction as a function of P. The small

values of P (high thermal resistance R) lead to eigenvalues of the odd functions

which are thus quite close to k

, which are the eigenvalues of the even functions

(Figure 8.15b). The discontinuity at the origin

2cos

k

of the odd eigenfunctions

is strong, and the thermal flux

1212

sin



between the two blocks is all the

smaller as k is large. The absolute values of the odd and even eigenfunctions are thus

very close in each of the two continuous media. A homogenization of the

temperature occurs in each block, the thermal flux

1212

sin



between them

being essentially limited to the first odd mode.

If the thermal resistance R tends to zero, P becomes large and the eigenvalues

12 

tend to the odd eigenvalues

k

of the total isolated system. We thus

find the odd eigenfunctions



sin



of the conduction problem for an

insulated wall (and of course, the temperature continuity at the origin).

In expression [8.17] of the modal development of the temperature, the

dimensional time constant

of each mode is directly related (formulae [8.33] and

[8.36]) to the corresponding eigenvalue /

444 Fundamentals of Fluid Mechanics and Transport Phenomena

a/ A

For small values of P, the first term of the development of /

as a function of P

is equal to

P2 (equation [8.54]). Substituting this value into the above expression

and replacing P by

A , we find for the time constant

AAA

We find the time constant of the thermodynamic model of section 8.3.1.2 in the

particular case where we have R' = 0, with

m .

8.3.2.3.4.

Expression of the solution

The complete solution of the problem can be obtained from formula [8.18] as the

development of the difference

)0,()0,( xTxT

 as a series of eigenfunctions of the

problem; these are orthogonal if the operator of the problem is self-adjoint

(Appendix 4). The verification of this property can be checked easily by separately

considering the intervals [-1,0

–

] and [0

,1]; and taking account of the condition



01' g , we have, after integration by parts, for p not equal to q:



³³³







'''

xdggggdggxdgg

qpqpqpqp

Proceeding in a similar manner for the other interval, we obtain:

   









00000000

''''

pqqppqqp

pqqp

gggggggg

xdgggg

Taking account of conditions [8.48] for the thermal resistance at x = 0 and after

replacing

and

by their expressions taken from equation [8.50], we see that

the integral

'' ''

pq qp

gg gg dx



¯



¡°

¢±



is zero if p is not equal to q:



'' '' 2 2

pq qp p q pq

gg gg dx ggdx



¯

 

¡°

¢±

¨¨



The eigenfunctions g

and g

are orthogonal for the scalar product

xdfggf



!  .

Thermal Systems and Models 445

The complete solution [8.18] can be written:



/









)

()

cos()

()

(

xgecxkectxTtxT

[8.55]



>@>@



with 0 1 2

00 00 12















 

³³

 



  

ek e

T( x, ) T ( x, ) g ( x)dx

c k , , ,...,n,...

g(x)dx

c T( x, ) T ( x, ) dx; c T( x, ) T ( x, ) cos( k x )dx k , ,...,n,...

8.3.2.4. Modal representation of systems and number of parameters

The modal representation of a discrete system consists of replacing the n state

variables



, functions of time, with n coefficients c

of the expression of the

solution on the basis of the eigenfunctions whose time dependence is known. We

thus see that, assuming the eigenfunctions to be known, the number of numerical

values (series development coefficients) which characterize the solution decreases

with time.

The same is true for the preceding models for continuous media, for which we

replace the temperature distribution T(x,t) in two continuous variables by a

denumerable sequence of series development coefficients c

[8.55] of eigenfunctions

associated with the physical model used. In a manner analogous to the development

of a periodic function in a Fourier series, the information necessary to characterize

the solution has been considerably reduced through the use of basis functions

adapted to the problem.

Furthermore, these developments offer the advantage that they provide an

organization of information. We saw in Chapter 7 that the frequencies associated

with the terms of a Fourier series are greater as the order of these terms is high. This

thus results in criteria regarding: the nature of the approximation which has been

made where only a limited number of terms are retained, and regarding the sampling

of the corresponding temporal signals (Shannon’s theorem). The modal

representation of thermal systems indicates that the wealth of information decreases

as time increases. For continuous media, this information diffuses from the wall and

becomes progressively poorer. The results are that the representation using space-

time numerical data (x,t) is very variable. During the first instants, we need to

discretize the time and near-wall zones very densely, while the central zone of the

wall is not subjected to any phenomenon. For larger times, the entire wall needs to

be discretized, but less densely, and the same goes for the time variable. We will

note that, as the modes vanish successively, the quantity of information contained in

446 Fundamentals of Fluid Mechanics and Transport Phenomena

the solution decays with time, the effect of the second law of thermodynamics

(increasing entropy) being to homogenize the temperature.

8.4. External representation of linear invariant

systems

8.4.1. Overview

Transitional solutions of differential system [8.13] of n linear first order

differential equations with n unknowns form a vector space of dimension n. They

allow the characterization of all possible states described by [8.13]. In practice, it

often happens that the initial data of a category of problems is of reduced number p,

the system starting for example from a given standard state (rest for example). The

transitional solutions which correspond to these initial conditions belong to a family

which depends only on these p parameters. The state representation of a system of n

state variables thus constitutes an overly detailed model. Rather than establishing a

state representation, we can be satisfied with the study of system responses by

means of an external representation by limiting ourselves to the effective inputs and

initial conditions.

Consider for example a linear invariant system for which the inputs are zero.

This is the modeling of an isolated homogenous system which evolves towards

equilibrium and which is characterized by a zero value for the state vector and the

outputs. Suppose that we impose as initial conditions given values (step functions

for example) for p components (p < n) of the state vector, the other components

being zero. This initial vector must be decomposed on eigenvectors of the

homogenous system, and apart from some particular cases, none of these

components is zero. The responses to these excitations comprise the n eigenmodes,

but they belong to a family of only p parameters which form a vector sub-space of

dimension p of the output space, which we can study directly.

8.4.2. External description of linear invariant systems

8.4.2.1.

Impulse response

The solution corresponding to diverse inputs and initial conditions is the sum of

solutions for each of the inputs and initial conditions taken separately, the others

being considered zero. This superposition property for solutions of time-invariant

linear systems allows us to separately study the response to different inputs and

initial conditions.

Consider firstly a system with a single input u

to which we apply a Dirac

distribution at the initial instant, the system being initially at rest; the output vector

Thermal Systems and Models 447



represents the evolution of the system outputs to this impulse on the first

input. Now, any given input



can be considered as the superposition of Dirac

distributions:

    

WWGW

dtutu 

The response



of the system outputs to the excitation



can be written:

    

WWW

duthtY

111

 [8.56]

The impulse response of the output vector therefore makes the characterization

of the response of a stationary linear system to any input excitation possible.

Proceeding similarly for the group of p inputs, we obtain a rectangular matrix

  





ththth

YpYY

,...,,

of dimension q

p formed with the p corresponding output

vectors, the entire group of which constitutes the matrix

)(tH

of the impulse

response output vectors of the system. This allows us to calculate the output

corresponding to any given input vector

)(tU :

    

WWW

dUtHtY



[8.57]

The impulse response matrix

)(tH

constitutes an external description of the

system taken to be initially at rest. Easily realizable experimentally, it can be

obtained using only impulse excitations, without any knowledge of the internal

variables in the initial reference state. It also allows us to describe the evolutions

corresponding to the given non-zero initial states of the system which are obtainable

by using suitable impulses on the inputs (section 8.2.1.5).

As an input vector is usually of smaller dimension than the state vector, the

impulse response matrix

)(tH

is a reduced model of the system adapted to its

operating conditions and which is not equivalent to the state representation of

section 8.1.2.

This matrix contains p*q time functions whose useful duration is equal to a

number of times the largest damping time constant. The quantity of information is

here much greater than in the case of the state representation: this is the result of the

absence of a model. For the linear time-invariant

thermal system, each of the

Responses of stable systems usually studied in fluid mechanics and acoustics present an

oscillatory damped character.

448 Fundamentals of Fluid Mechanics and Transport Phenomena

functions is a sum of decaying exponentials which we can seek to identify

approximately, at least for the first of these. In the absence of a state representation,

any interpretation of results is difficult and the obtaining of the structure of the

eigenmodes of the system is problematic.

The result of formula [8.57] is that at a given instant, the state of a linear

invariant system depends only on the inputs belonging to a past which is at most

equal to the duration of the impulse response.

NOTE – The preceding procedure can also be applied to a state vector X(t). The

application of a Dirac impulse as an input of index i provides the state vector



Operating in a similar fashion on the ensemble of inputs, we obtain the matrix

)(tH

of impulse responses of the state vector, of dimension n

p, which allows us

to obtain the response of the state vector to any given input U(t):

    

WWW

dUtHtX



However, the direct measurement of state variables is not easy in general, and

the impulse response matrix

)(tH

of the state vector is only of limited interest.

8.4.2.2.

Inputs-outputs analytic representation

The complete external representation of a system can be obtained from its state

representation, cast in the form of a scalar differential equation of order n (section

5.1.1 and section 8.1.2) in a scalar state variable x (t). Let us take the simple

example (n = 3) of the state representation with a single output y(t):

''';''''''

2103210

xdxdxdyuxaxaxaxa  

[8.58]

Calculating the linear combination

'''

210

ududud 

and eliminating x(t) and its

derivatives with [8.58], we obtain a differential equation for the output y (t):

'''''''''

2103210

udududyayayaya  

[8.59]

The method can be generalized to a differential equation of arbitrary order:

  

¦¦

jkj

xdyuxa

;

[8.60]

We obtain:

Thermal Systems and Models 449



 

¦¦¦¦



jki

udxdaya

0000

[8.61]

The inverse passage of the preceding external representation to a state

representation can be achieved easily, the coefficients of relations [8.60] and [8.61]

(or [8.58] and [8.59]) being identical.

The representation of a dynamic system of n variables, effected by means of a

differential equation of order n, can be replaced by a relation of a differential

nature between the inputs and the outputs. However, obtaining the preceding

external representations by means of measurements, without any knowledge of the

structure of the system, is impractical for complex systems: the evaluation of the

temporal derivatives obtained from differences between measurements lead to errors

which will be greater as the order of the differentiation is increased.

8.4.2.3.

Example of a thermal system with two variables

As an example, consider the state representation of the two-component system of

section 8.3.1.2:

2222121

21212111

; uTaTaTuTaTaT   [8.62]

where the quantities u

and a

are defined in equation [8.21]:



2,1

;

111

21122211

 i

mCR

RRmC

iex

Differentiating the first equation [8.62] and eliminating

by means of second

relation [8.62], we obtain a second order differential equation satisfied by T



212

1122

12211121122211

uauuaTTaaTaaaa   [8.63]

Taking the output variable in the form [8.58]:

1110

TdTdy 

, the external

representation can be obtained from [8.59]:



''''

10221121122211

ududyyaayaaaa   [8.64]

with:

212

1122

uauuau  .

450 Fundamentals of Fluid Mechanics and Transport Phenomena

8.4.2.4.

Laplace transforms and operational transfer matrices

We have already seen in Chapter 7 the value of Fourier transforms for the study

of oscillatory signals. The Laplace transform (Appendix 1) presents an analogous

interest for the study of aperiodic signals and damped systems. The Laplace

transform L

of a function f(t) is defined by the relation:

 



dtetfpL

[8.65]

It possesses diverse properties which are analogous to those of the Fourier

transform (section 7.3.4.2); in particular, the Laplace transform of the derivative

function f is written:

  

fppLpL



This property allows us to transform the system of differential equations and the

initial conditions into a system of algebraic equations between the transforms of the

variables. For example, the differential equation transform:



tukxxfxm 



can be written:





 

LxpxLkpfpm  0'0

or:



   

kpfpm

xpxpL





[8.66]

We thus obtain the transform of the complete solution written as a function of

the initial conditions and the transform L

(p) of the right-hand side (the input). All

that remains is to perform the inverse transform (Appendix 1).

The transform linearity allows it to be applied to a vector or to a matrix of

functions. For the initial conditions



0X , the Laplace transform of the state

representation [8.1] of a linear invariant dynamic system can be written:



XYUXX

LDLLBALXpL .;.0  

Thermal Systems and Models 451

We can thus deduce the transforms of the solution



tX and of the output vector



tY :



-1

0: . .

XUYX

Lp pIA BLp X L DL

¯

  

¢±

[3.67]

As the inverse of a matrix M is equal to the ratio between the transpose of its

comatrix

and its determinant ([HAR 98]), the elements of the matrix



1

 ApI

rank n are rational fractions whose denominator is equal to

ApI 

, the numerator

being a polynomial in p whose order is at least equal to n. This rational fraction can

be decomposed into simple elements associated with the poles (zeros of the

denominator) which are the eigenvalues of the system studied. Each of these

elements is the Laplace transform of the real or complex exponential functions

which correspond to the eigenmodes of the system studied.

The matrix

  

BApIDpH



 is the operational transfer matrix of the

system:

     

pLpHpLBApIDpL

UUY

...



[3.68]

As the Laplace transform of a Dirac distribution at instant t = 0 is equal to 1, the

transfer matrix



pH is the Laplace transform of the impulse response matrix

)(tH

The Laplace transform is particularly useful in the domain of system controls

which are essentially beyond the scope of this textbook, despite applications in the

domain of flow and transfer phenomena.

8.5. Parametric models

8.5.1. Definition of model parameters

A parametric model can be defined as an exact or approximate solution whose

state vector X(t) can be written in the form of a combination (linear or otherwise) of

some state vectors X

(t) independent of the inputs; the coefficients Pj of this

combination are time functions which are deduced from the input vector

)(tU

(the

coefficients Pj are functionals of



tU ). For a linear combination, we have:

I.e. the matrix of cofactors of each element.