Peube J-L. Fundamentals of fluid mechanics and transport phenomena
Подождите немного. Документ загружается.


452 Fundamentals of Fluid Mechanics and Transport Phenomena
¦
j
jj
tUPXtX
[8.69]
Expression [8.69] is quite analogous to a series development of eigenfunctions.
Like these, the vectors
X
j
are
universal
, as they do not depend on any particular
inputs of the problem. The coefficients
P
j
are parameters characterizing, in a simple
manner, the solution represented at each instant as a basis composed of state vectors
Xj
which are often chosen in order to best represent the solution
for a class of given
inputs
. Their non-dimensional expressions are often called
form parameters
, as they
characterize the relative value distribution of the state vector components (see
example in section 8.5.2). We have adopted the terminology
parametric model
in
reference to the idea of form parameters often used in fluid mechanics.
The output vector
XDY
.
can be written in an analogous form [8.69] with the
universal vectors
D X
j
and the parameters
P
j:
¦
j
jj
tUPXDtXDtY
[8.70]
We can note that the solution of the system obtained by solving equations [8.14]
and [8.15] of the state representation using the variation of constants method is not
in general of the form [8.69] or [8.70].
Solutions of parametric type can also be obtained in an approximate manner by
means of global methods. Some examples of parametric solutions of linear systems
will be covered in the following section. Such exact or approximate solutions are
also used in fluid mechanics for the study of the boundary layer (Blasius and
Howarth series, Görtler series, Karman-Polhausen global method, etc. ([SCH 99],
[YIH 77])).
The value of the parametric methods is quite significant:
–
with the objective of understanding and interpreting physical phenomena:
the
values of the parameters
P
j
allow in effect the classing of excitation situations by the
function
U
(
t
) by characterizing these situations using simple analytical forms of the
solution. We will see examples of the application;
–
for writing models of complex systems:
expression [8.70] is an
external explicit
representation
of a system in which the inputs and outputs are variables which
characterize the interactions between neighboring systems; limited to a small
number of terms, it constitutes an approximate representation which is particularly
useful for modeling of interacting systems.

Thermal Systems and Models 453
8.5.2. Established regimes of linear invariant systems
8.5.2.1.
Systems described by a state representation
In section 8.2.2.1 we defined an
established regime
as a solution of a differential
system whose expression does not contain transitional terms associated with the
initial conditions. The solutions of discrete time-linear linear systems can be
cast
in
a simple parametric form, at least when the inputs do not vary too rapidly. The
guiding idea of the method has already been outlined in section 6.4.2.6; it consists of
considering the unsteady term of state equation [8.1] as a perturbation [SAD 93]. By
introducing the parameter
H
which we will take to be equal to one in the following,
the state equation [8.1] can be written:
UBXA
dt
dX
..
H
[8.71]
We seek the solution of equation [8.71] in the form:
¦
f
0
tXtX
i
i
H
[8.72]
By substituting expression [8.72] into equation [8.71], and by identification
according to the increasing powers of the parameter
H
, we obtain the system:
!!!!!
!!!!!
;.
;.;.
;0..
'
12
'
1
'
01
0
tXtXA
tXtXAtXtXA
tUBtXA
ii
[8.73]
Assuming the matrix A to be invertible, we deduce:
!!!!!
!!!!!
;''.
;.;'.
;.
3
2
)(12
1
1
0
tUBAtX
tUBAtXtUBAtX
tUBAtX
ii
i
Substituting and taking
H
to be formally equal to 1, we finally obtain:

454 Fundamentals of Fluid Mechanics and Transport Phenomena
>@
»
¼
º
«
¬
ª
¦
¦
f
f
1
)(11
1
)(11
......
..
tUBACtUDBCAUDXCtY
tUBAtUBAtX
ii
i
ii
[8.74]
Series [8.74] is a general solution to the established regime of system [8.1].
Independent of the initial conditions, it converges if the successive derivatives of the
input vector U do not vary too quickly, for example if the quantities
tu
i
are
bounded by
i
k
1
/ (/
1
: smallest eigenvalue of the matrix A, k constant).
The idea of form parameters can be introduced by means of the simple example
of a system with a scalar input
tu . Solution [8.74] can thus be written:
»
»
¼
º
«
«
¬
ª
¦
f
1
)(
11
..
i
i
i
tu
tu
BABAtutX [8.75]
The parameters
tutu
i
are form parameters of the problem and determine
the structure of the solution.
The Laplace transform allows the preceding results to be retrieved by giving an
explicit expression of the term
-1
U
p
IABLp
of the established regime of
equation [8.67]. We obtain:
>@
...
2211
1
11
1
nn
ApAppAIApAIAApI
or:
>
@
U
nn
UX
LBApAppAIALBpIAL .........
2211
1
This expression is indeed the Laplace transform of the first equation [8.74].
NOTES
–
1) Temporal series of the form [8.74] (or [8.76]) which describes in parametric
form how the established regimes can be derived from responses obtained by the
convolution integral [8.57] in which we perform a Taylor series development. For
example, for the state vector, taking account of the commutativity of the convolution
product, we have:

Thermal Systems and Models 455
2
00
2
00 0
. ' ' ...
2
'. '' ...
2
Xt Ut H d Ut Ut Ut H d
Ut H d Ut H d Ut H d
dd
dd d
¯
¡°
¡°
¢±
¨¨
¨¨ ¨
2) The perturbation method used can also be applied to non-linear equations.
8.5.2.2.
Case of representation by differential equations of order n
The preceding method can be applied to write the established system and the
solution to the differential equation [8.60] of order n, representing system [8.1], with
a single state variable x (t):
¦¦
1
01
;
n
k
k
jkj
n
i
i
i
xdytuxa
We obtain, for the established regime:
pLpdLpLpLpa
x
n
k
k
jkjyux
n
i
i
i
»
¼
º
«
¬
ª
¸
¸
¹
·
¨
¨
©
§
¦¦
1
01
;
or:
pL
pa
pd
L
pa
pL
pL
u
n
i
i
i
n
k
k
jk
jy
n
i
i
i
u
x
¦
¦
¦
1
1
0
1
;
The established regime for small values of p can be obtained by calculating the
above fraction series development following the increasing powers of p, for
example, by means of a division following increasing powers.
By limiting ourselves to the third term, we obtain:
pLp
a
a
a
aa
a
a
p
a
a
a
a
p
a
a
a
p
a
a
a
pL
pL
u
ii
u
x
¸
¸
¸
¹
·
¨
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
...
2
1
1
1
3
3
0
3
1
2
0
12
0
32
0
2
2
0
2
1
0
1
0
0
0
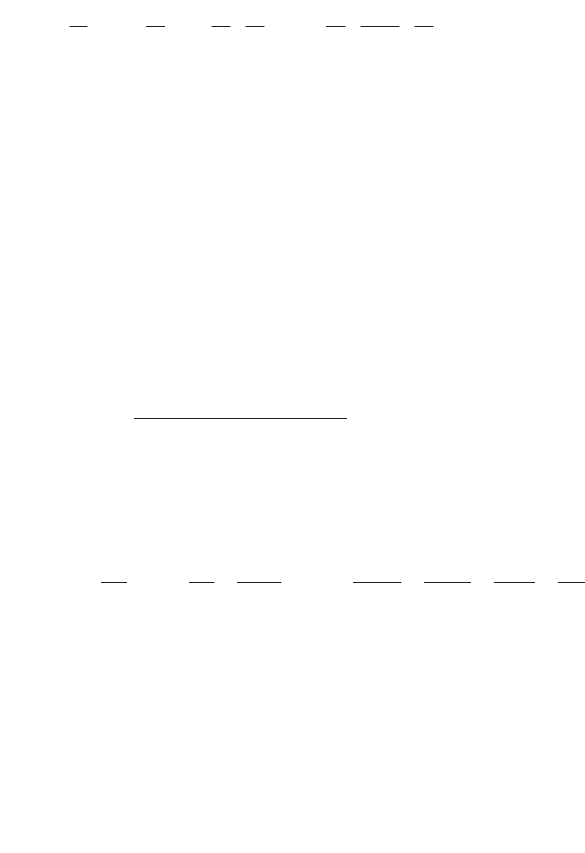
456 Fundamentals of Fluid Mechanics and Transport Phenomena
whence the parametric expression for the state variable x(t):
...'''"'.
3210
tuAtuAtuAtuAtx [8.76]
23
3
112 211
01 2 3
232 234
0000 000
2
1
with ; ; ; ;....
a
aaa aaa
AA A A
aaaa aaa
8.5.2.3.
External representations
The same procedure can be employed for the input-output representation [8.59]:
'''''''''
2103210
udududyayayaya
for which the Laplace transform can be written:
pLpdpddpLpapapaa
uy
2
210
3
3
2
210
or:
pL
papapaa
pdpdd
pL
uy
3
3
2
210
2
210
By dividing the fraction in p following increasing powers, and then returning to
the space-time domain, we obtain the differential representation:
..."'
0
2
2
0
11
2
0
20
3
0
2
10
2
0
10
0
1
0
0
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
tu
a
d
a
ad
a
ad
a
ad
tu
a
ad
a
d
tu
a
d
ty
8.5.2.4.
Harmonic established regimes
A system can also be characterized in spectral space. We thus proceed in a
manner analogous to the case of impulse excitation, but with harmonic excitations in
complex form
tj
e
Z
. The established harmonic regimes of the linear invariant
systems can be studied by means of the complex amplitudes method by searching
for solutions in the form
tj
eXX
Z
ˆ
, where we denote by
M
ˆ
the constant
complex matrix associated with the matrix function
tj
eMtM
Z
ˆ
, the temporal
derivation having been replaced by a multiplication by j
Z
. System [8.1] can be
written:

Thermal Systems and Models 457
UBXAXj
ˆˆ
.
ˆ
Z
[8.77]
Solving linear algebraic system [8.77] makes it possible to calculate complex
amplitudes of the state vector
)(
ˆ
Z
X and the output vector )(
ˆ
Z
Y for all values of
the pulsation
Z
. We obtain complex algebraic equations analogous to those obtained
by Laplace transform for the established regimes, where the variable p is replaced by
j
Z
. The complex vector amplitudes )(
ˆ
Z
X and )(
ˆ
Z
Y can be written:
1
1
ˆˆ
() .();
ˆˆˆ
() ().() with: .
X $ j$ IA BU$
Y $ H $ U $ H $ Dj$ IA B
The matrix
)(
Z
H is the transfer matrix of the system between the inputs and the
outputs. It is the Fourier transform of the impulse response matrix.
The harmonic regimes of external representations obtained above can be
obtained in the same way. For example, from relation [8.59] we can derive the
complex amplitude of the output
y
ˆ
as a function of the input
ˆ
():
u $
u
aajaa
djdd
y
ˆˆ
2
31
2
20
2
210
ZZZ
ZZ
The parametric representations obtained earlier can be written in the harmonic
regime, by performing a series development in increasing powers of j
Z
. For
example, with the discrete system of equations [8.1], we have, from [8.74]:
UBAjCDYUBAjX
n
n
n
n
n
n
ˆ
.
ˆ
.;
ˆ
.
ˆ
1
0
1
0
¸
¸
¹
·
¨
¨
©
§
f
f
¦¦
ZZZ
The preceding series developments in
Z
are a valid approximation for the low
frequencies. We will obtain in section 8.5.3 an estimation of the radius of
convergence of the preceding series in
Z
in an example.
In the study of certain vibration problems (mechanical, electrical and
electromechanical, acoustics), we define impedances which are functions of the
transfer between the intensive quantities (forces, electric potentials, acoustic
pressure) and the flux of associated extensive
7
quantities (velocity, electrical
intensity, acoustic flux) evaluated at the same point. These impedances are in fact a
7
These extensive quantities can be reduced, for instance in the case of mechanical
impedances.

458 Fundamentals of Fluid Mechanics and Transport Phenomena
particular kind of transfer function. We will assume that these ideas are known to
the reader at least in the domain of electricity.
NOTE – The different external representations discussed above are equivalent. In
practice, we use the form which is best adapted to the problem under study.
8.5.3. Established regimes in continuous media
8.5.3.1. Systems described by a continuous state representation
Consider the cylinder of axis Ox, of cross-section limited by the arbitrary curve
C (Figure 6.13 of section 6.4.2.6) and on the wall of which we impose the uniform
temperature T
w
(t). The 2D temperature distribution
tzyT ,, satisfies the equations
and conditions:
tTtzyTCzyTa
t
T
w
'
w
w
,,:,:with; [8.78]
Let us take the dimensionless variables:
2
~
;
~
;
~
AAA
tatzzyy
Equation [8.78] becomes:
tTtzyTCzyT
t
T
w
~~
,
~
,
~
:
~
,
~
:with
~
~
'
w
w
[8.79]
Let us look for a solution in the form [PEU 84]:
¦
f
0
)(
~
)
~
,
~
()
~
,
~
,
~
(
i
i
wi
tTzygtzyT [8.80]
Substituting into [8.79] and identifying the terms corresponding to the
derivatives
tT
i
w
~
)(
, we obtain:
01021 1
0; ; ; ... ; ...
nn
ggggggg
'' ' '
with the boundary conditions:
0
, : , 1; , 0 1,..., ,...
i
yz C g yz g yz i n
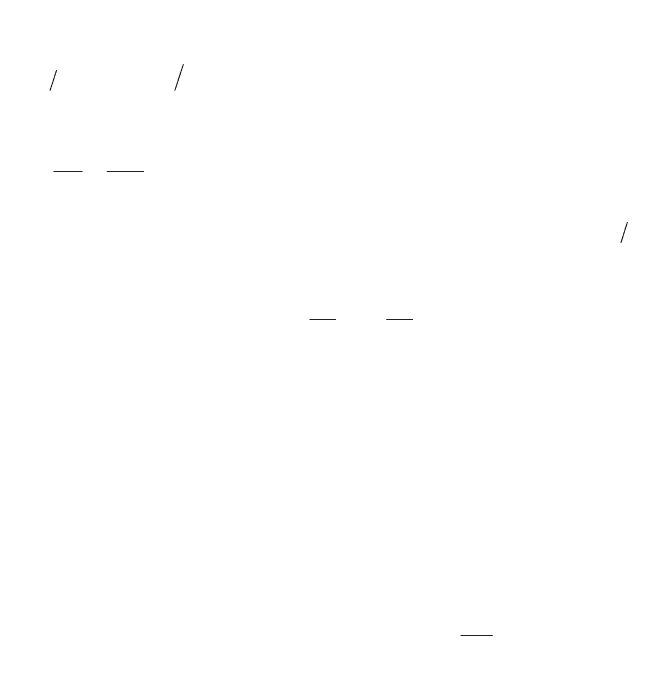
Thermal Systems and Models 459
The functions
zyg
i
~
,
~
can thus be calculated from place to place. The reader
can immediately verify that these are identical to the corresponding functions of the
unsteady flow problem of a viscous fluid in a cylindrical tube of contour C (section
6.4.2.6), a difference of unity excepted for the value of index i.
The method used can be applied to continuous systems containing discrete
elements. Let us take the system constituted of two walls separated by a thermal
resistance (section 8.3.2.3.1). Consider here the case where one of the faces is
maintained at constant temperature
0
A
T , the other face at abscissa +
A
being
subject to the variable temperature T
w
(t). Taking the dimensionless variables [8.33]
(
A
xx
~
and
2
~
A
tat ), we obtain the heat equation on the intervals [-1,0] and
[0,1]:
2
2
; with:-1 x 0, 0 x 1
TT
tx
ss
bb
ss
[8.81]
As the thermal resistance R is characterized by relation [8.49] (with
RP
O
A
),
we have the boundary conditions (section 8.3.2.3.1):
>@
)0()0(
~~
;
~
1;01
00
¸
¸
¹
·
¨
¨
©
§
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
TTP
x
T
x
T
tTTT
w
[8.82]
We can easily verify that the equation and the preceding boundary conditions
possess a solution analogous to [8.80]:
¦
f
0
)(
~
~
)
~
,
~
(
i
i
wi
tTxgtxT [8.83]
The functions
xg
i
~
satisfy the following successive relations and conditions:
>@
;11;01
0000;011:,,1
~
~
;
~
~
;
~
~
;0
~
00
''
1
''
1
''
20
''
1
''
0
f
gg
gg
R
ggggi
xgxgxgxgxgxgxg
iiiiii
nn
O
A
!
!!!
We can easily calculate the first two functions:
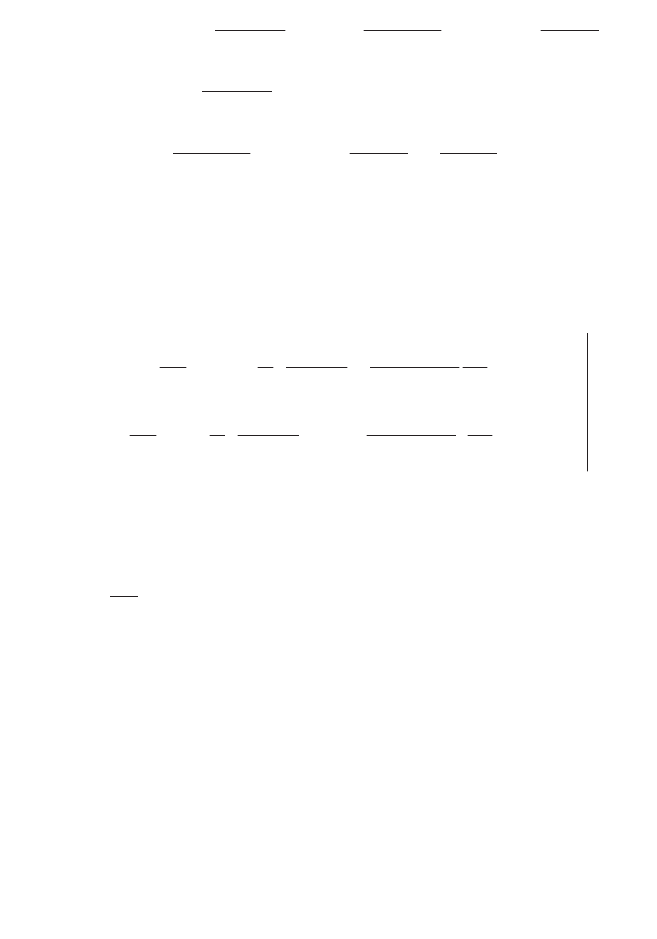
460 Fundamentals of Fluid Mechanics and Transport Phenomena
2
1
~
21
68
1
~
216
1
;1
21
1
~
10
21
68
1
~
216
1
~
;
21
1
~
0
~
1
2
2
1
0
2
10
»
¼
º
«
¬
ª
d
»
¼
º
«
¬
ª
d
x
P
P
x
P
xP
g
P
xP
gx
P
P
x
P
xP
g
P
xP
gx
[8.84]
The first function
xg
~
0
is the temperature distribution in the steady regime.
The reader can easily certify that this corresponds to the thermal resistances in series
associated with two continuous media and to the resistance R. The thermal flux
density on the walls is derived from the following expressions:
¸
¸
¹
·
¨
¨
©
§
»
»
¼
º
«
«
¬
ª
¸
¸
¹
·
¨
¨
©
§
w
w
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
w
w
!
A
A
A
!
A
A
A
A
A
tT
a
P
PP
P
tTP
x
T
q
tT
a
P
PP
P
tTP
x
T
q
p
p
Tp
p
p
Tp
'
2
2
'
2
2
213
34
1
21
213
34
21
O
O
O
O
[8.85]
More generally, M being an operator which only contains spatial derivatives, let
us consider equation [8.86]:
t
f
fM
w
w
[8.86]
which possesses parametric solutions of the form:
¦
f
0
)(
,,),,,(
i
i
wi
tTzyxgtzyxT
The first function
zyxg ,,
0
is the spatial distribution of the function f in the
steady regime corresponding to the steady conditions imposed which define the
reference temperature T
w
. The universal functions g
i
satisfy the successive
equations:
010 1
,, 0; ,, ,, ; ,, ,, ;
nn
Mg x y z Mg x y z g x y z Mg x y z g x y z
!!
For example, the thermal conduction equation for a cylindrical problem in a
heterogenous medium can be written:
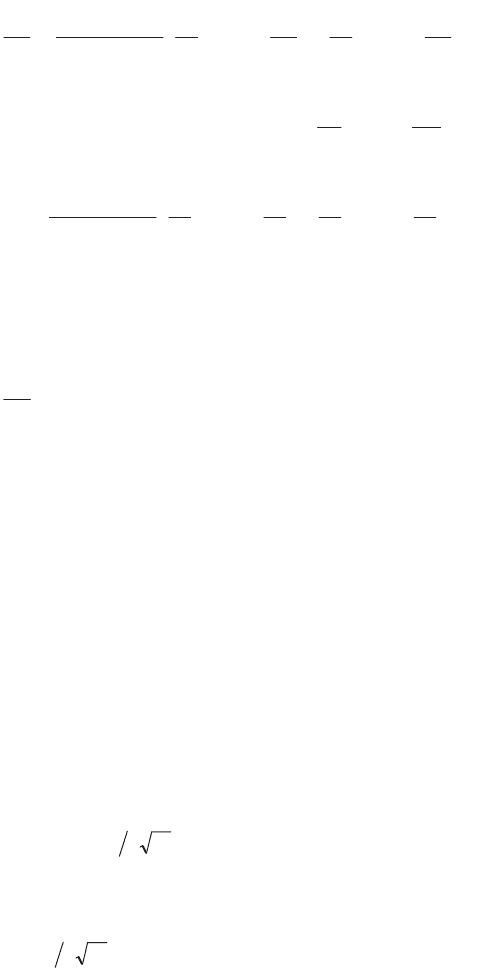
Thermal Systems and Models 461
»
»
¼
º
«
«
¬
ª
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
y
T
zy
yy
T
zy
yzyczyt
T
,,
,,
1
OO
U
It corresponds to the operator
,,:
T
Mayz yz
yy
¬
ss
ss
®
»
»
¼
º
«
«
¬
ª
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
y
zy
yy
zy
yzyczy
M ,,
,,
1
OO
U
The case where the cylinder is the seat of a volume heat source
V
T
(t) can be
treated in an analogous manner to that of the problem of viscous flow in a
cylindrical tube, as studied in section 6.4.2.6:
; with: , : , , 0
T
T
taT yzCTyzt
t
'
s
s
The equations of the universal functions g have been established in section
6.4.2.6. The parameters P
j
of formula [8.69] which characterize the input are here
the successive derivatives
t
i
T
V
.
8.5.3.2.
Established boundary layer regimes
The regular perturbation method used for parametric solutions in a finite domain
can be extended to the case of boundary layers, on the condition that the problem be
cast as a regular problem. Let us reconsider the example of a thermal shock in a
semi-infinite medium as described in section 5.4.5.4 (and applied at the end of
section 8.3.2.2.2) and verifying the heat conduction equation [8.78] but with the
variable wall temperature T
w
(t). In the plane (x, t) we have a singular perturbation in
the vicinity of x = 0 where the solution obtained presents very different scales: for
small time values the spatial variations of temperature are rapid, whereas for large
time values they are slow. The convergence of solutions close to this base solution
towards this solution cannot therefore be uniform. The variable adapted to the
boundary layer
atx 2
K
is defined as in section 5.4.5.4. We first of all perform
a change of coordinates
W
K
,, otx , in order that the difference between the two
solutions can be characterized in a uniform manner:
WKTWK
,,;2 txTtatx
Transformed heat equation [8.32] can be written:
