Презентация - Андреев В.К. Механика жидкости и газа
Подождите немного. Документ загружается.

В классической постановке теории пограничного слоя предполагается, что движение во внешней
области предварительно рассчитано, а внутреннее решение удовлетворяет усло
вию прилипания на
твердой стенке и должно асимптотически переходить во внешнее решение при удалении от стенки.
Пограничный слой играет основную роль в процессах динамического (сопротивление, подъемная
сила) и термодинамического (тепло– и массообмен) взаимодействия потока ре
альной жидкости или
газа с обтекаемым или твердым телом.
Уравнения Прандтля ламинарного пограничного слоя
Изучение движения вязкой жидкости в области пограничного слоя основывается на
интегрировании уравнений пограничного слоя, носящих имя своего создателя Прандтля.
Рассмотрим вывод уравнений пограничного слоя. В силу малости толщины пограничного слоя по
сравне
нию с размерами твердого тела и радиусами кривизны его поверхности будем считать сетку
параллельных контуру тела кривы
х и нормалей к ним прямоугольной декартовой системой координат
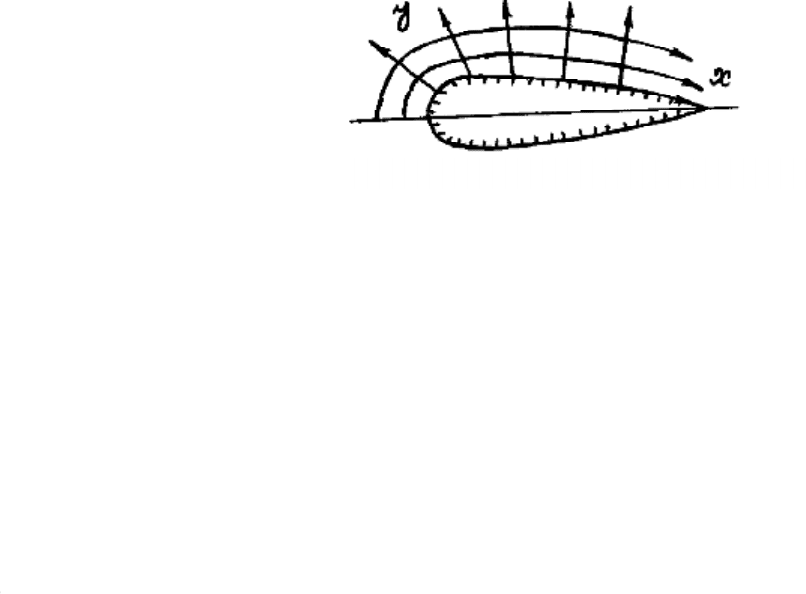
(x, y), начало координат поместим в переднюю точку обтекаемого профиля (рис. 15.1).
Рис. 15.1
Уравнение Навье-Стокса в этой системе координат будут иметь обычный для плос
кого движения
вид:
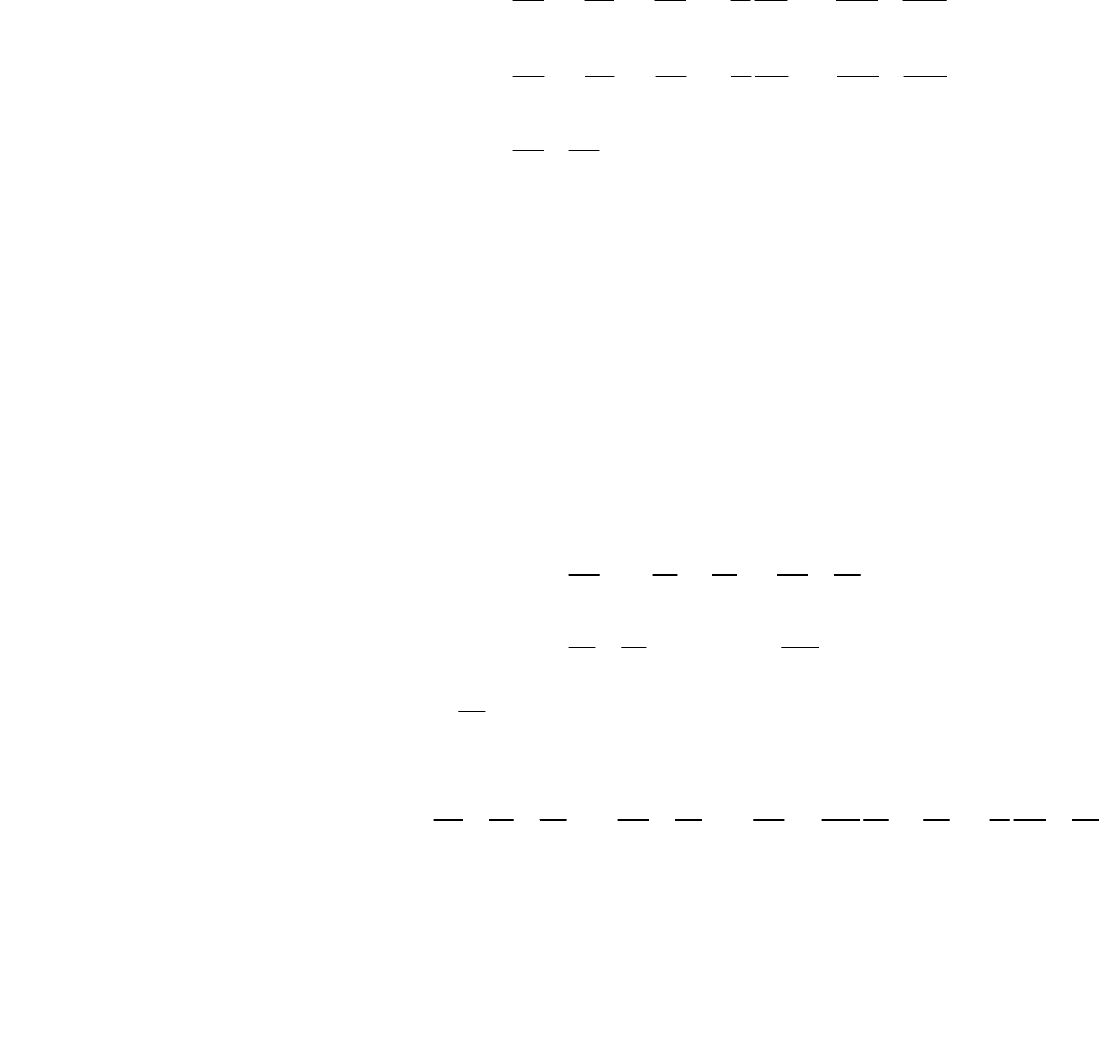
.0
v
),
vv
(
1v
v
vv
),(
1
v
2
2
2
2
2
2
2
2
=
∂
∂
+
∂
∂
∂
∂
+
∂
∂
+
∂
∂
−=
∂
∂
+
∂
∂
+
∂
∂
∂
∂
+
∂
∂
+
∂
∂
−=
∂
∂
+
∂
∂
+
∂
∂
yx
u
yx
y
p
yx
u
t
y
u
x
u
x
p
y
u
x
u
u
t
u
ν
ρ
ν
ρ
(15.1)
В тонком пограничном слое (толщиной
δ
) продольная составляющая скорости u
изменяется от
нулевого значения (u=0) на поверхности тела (y
=0) до некоторого конечного значения во внешнем
безвихревом потоке не
вязкой жидкости. Под внешней скоростью подразумевают скорость движения
идеальной жидкости на поверхности тела при отсутствии пограничного слоя.
Введем обозначения порядка основных величин (или масштабов), входящих в уравнение (15.1)
переменных: L – продольной координаты x;
δ
- поперечной координаты y;
0,0
v
u - скоростей u,
v
;
0
p -
давление;
0
t - время. За масштаб L можно взять хорду обтекаемого крыла
(т.е. характерную для потока
длину), за масштаб
0
u
- скорость набегающего потока. Порядки
δ
и
0
v
оценим из уравнений (15.1).
Обозначая порядок величины О, из уравнения (неразрывности) для одина
ковых порядков производных
находим
000
000
0
v
v
()~,~,
v
~v~.
uu
u
O
xLLy
uu
или
LL
δ
δ
δ
∂∂
=
∂∂
(15.2)
Характерное время
2
00
0
0
~,~ up
u
L
t ρ , тогда в первом уравнении все члены, кроме вязких, од
ного
порядка:
2222
0000000
0
1
~~,~,v~()~,~
uuuuuuu
uuup
u
ttLxLyLLxL
δ
δρ
∂∂∂∂
∂∂∂∂
,
что же касается вязких членов, то их порядки:
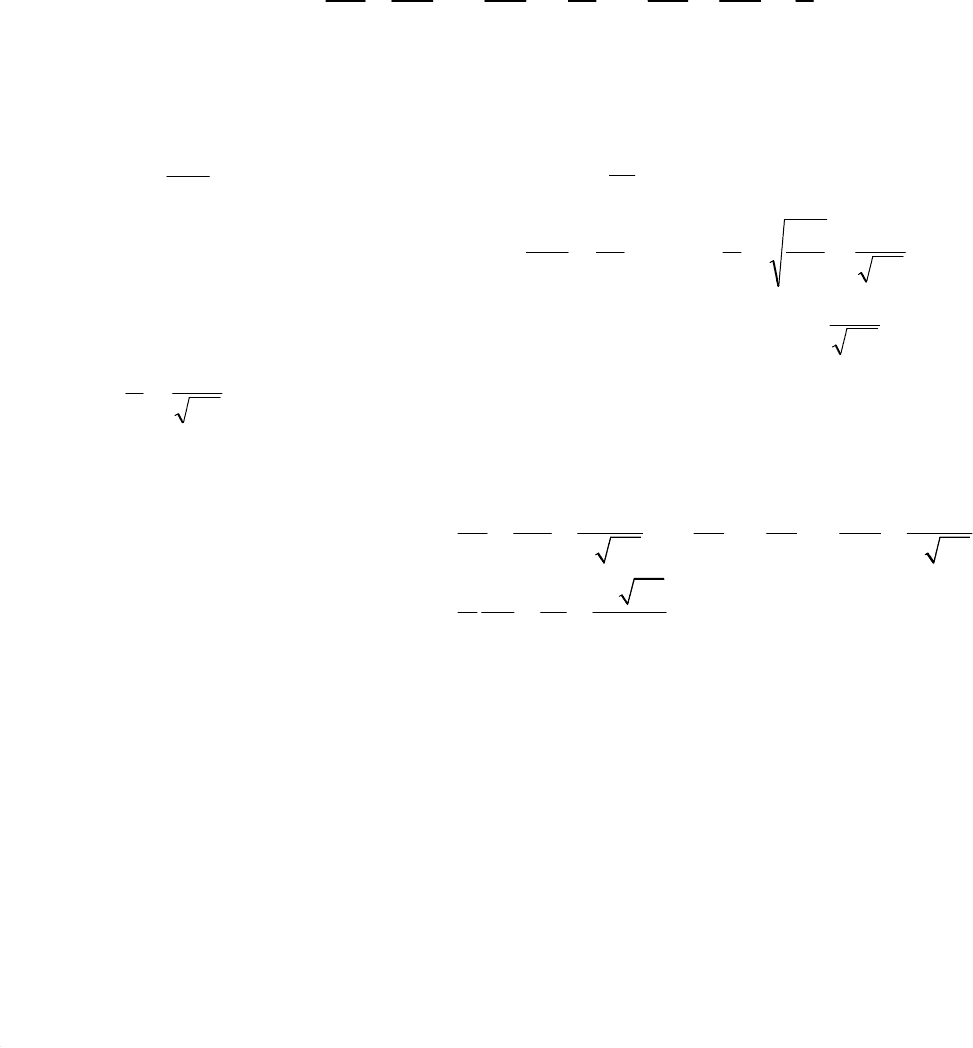
2222
2
00
222222
~,~:~()1
uuuuuu
xLyxyL
ν δ
ννννν
δ
∂∂∂∂
→<<
∂∂∂∂
. (15.4)
В силу определения пограничного слоя как области потока, в которой влияние вяз
кости
существенно в той же мере, как и инерционных сил и сил давлений, следует, что ос
тавленный вязкий
член
2
2
y
u
∂
∂
ν должен иметь тот же порядок
L
u
2
0
, что и все остальные члены (15.3), т.е.
L
uu
2
0
2
0
~
δ
ν
или
Re
1
0
==
LuL
νδ
. (15.5)
Следовательно, толщина пограничного слоя порядка
Re
1
. В пограничном слое (Re>>1)
величина
Re
1
==
L
δ
ε является основным малым параметром, характеризующим дви
жение вязкой жидкости при
больших числах Re.
Рассмотрим второе уравнение системы (15.1):
222
000
2
0
22
00
vvvv
~~,~v~~,
ReRe
Re
1
~~.
uuu
u
ttLxyy
LL
uu
p
yL
δ
ν
ρδ
∂∂∂∂
∂∂∂∂
∂
∂
(15.6)
Значит можно считать давление постоянным поперек пограни
чного слоя и равным давлению во
внешнем потоке.
Таким образом, оставляя главные члены в уравнениях при
∞
→
Re
, получим систему уравнений
плоского ламинарного нестационарного пограничного слоя (уравнения Прандтля):

2
2
1
v,
v
0.
uuupu
u
txyxy
u
xy
ν
ρ
∂∂∂∂∂
++=−+
∂∂∂∂∂
∂∂
+=
∂∂
(15.7)
Уравнения (15.7) представляют собой систему нелинейных уравнений в частных производных
второго порядка параболического типа.
Для решения конкретных задач необходимо присоединить к системе начальные и граничные
условия:
10
00
0,v00,
(,,)(,),
(,),
(,).
uпри y
utxyUtx при y
uuxy при tt
uuty при xx
===
→→∞
==
==
(15.8)
Для стационарных движений уравнения Прандтля с использованием функции тока примут вид
223
23
0
,
00,
(),
().
dUd
U
yxyxydxdy
при y
y
Ux при y
y
uy при xx
y
ψψψψψ
ν
ψ
ψ
ψ
ψ
∂∂∂∂
−=+
∂∂∂∂∂
∂
===
∂
∂
→→∞
∂
∂
==
∂
(15.9)
(Здесь учли, что для внешнего течения
1
U
dUp
dxx
ρ
∂
=−
∂
.)
Лекция 20.
Задача Блазиуса
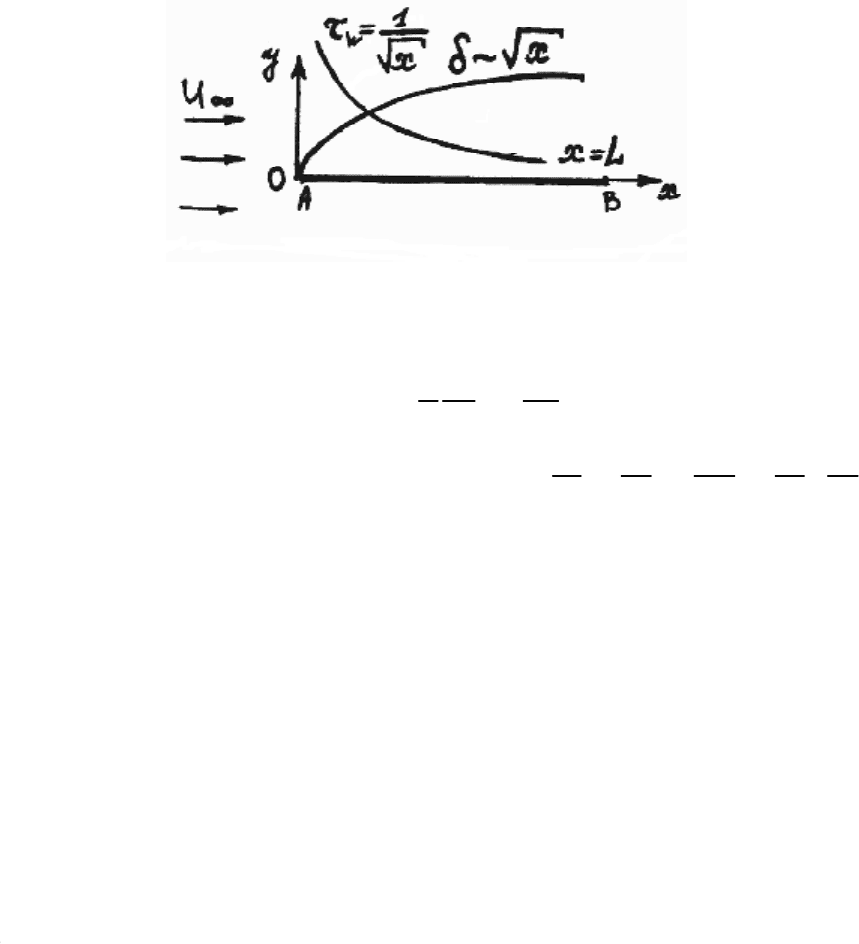
Рассмотрим пример автомодельных движ
ений продольного обтекания полубесконечной тонкой
пластинки (рис.15.2) безграничной несжимаемой вязкой жидкостью со скоростью на бесконечности
∞
U .
Рис. 15.2
При этом внешний поток, т.е. безвихревой поток идеальной жидкости, который фо
рмируется при
отсутствии пограничного слоя, однороден (
const
Uu
∞
==
). Уравнения пограничного слоя (15.7) в данном
случае будут иметь вид (
1
0
pU
U
xxρ
∂∂
−==
∂∂
):
2
2
v
v,0.
uuuu
u
xyyxy
ν
∂∂∂∂∂
+=+=
∂∂∂∂∂
(15.10)
Граничные условия:
0,v00,0,
,
0.
u при yx
uuпри y
uu при x
∞
∞
===>
→→∞
==
(15.11)
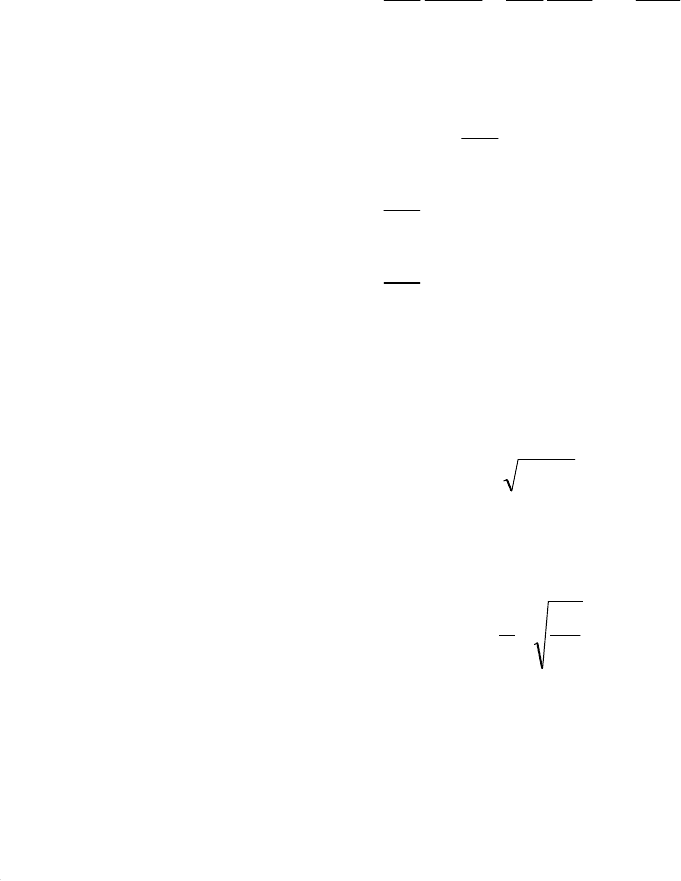
Наличие скачка в т. x
=0 делает ее особой точкой уравнений (15.10). В такой постановке задача была
впервые решена Блазиусом (1908
г.). Задача является автомодельной, т.е. систему уравнений (15.10)
можно свести к одному обык
новенному дифференциальному уравнению. В силу (15.9) система (15.10)
приводится к виду
.
3
3
2
22
yy
xyxy
∂
∂
=
∂
∂
∂
∂
−
∂∂
∂
∂
∂ ψ
ν
ψψψψ
(15.12)
Граничные условия:
0,00,0,
,
0.
при yx
y
uпри y
y
u при x
y
ψ
ψ
ψ
ψ
∞
∞
∂
===>
∂
∂
→→∞
∂
∂
==
∂
(15.13)
Можно показать, что задача сводится к определению функции тока од
ной переменной (это
следует из того, что решение не зависит от длины L). Полагая
)(ηϕνψ xu
∞
= , (15.14)
где
x
u
y
ν
η
∞
=
2
1
, (15.15)
вычисляя производные
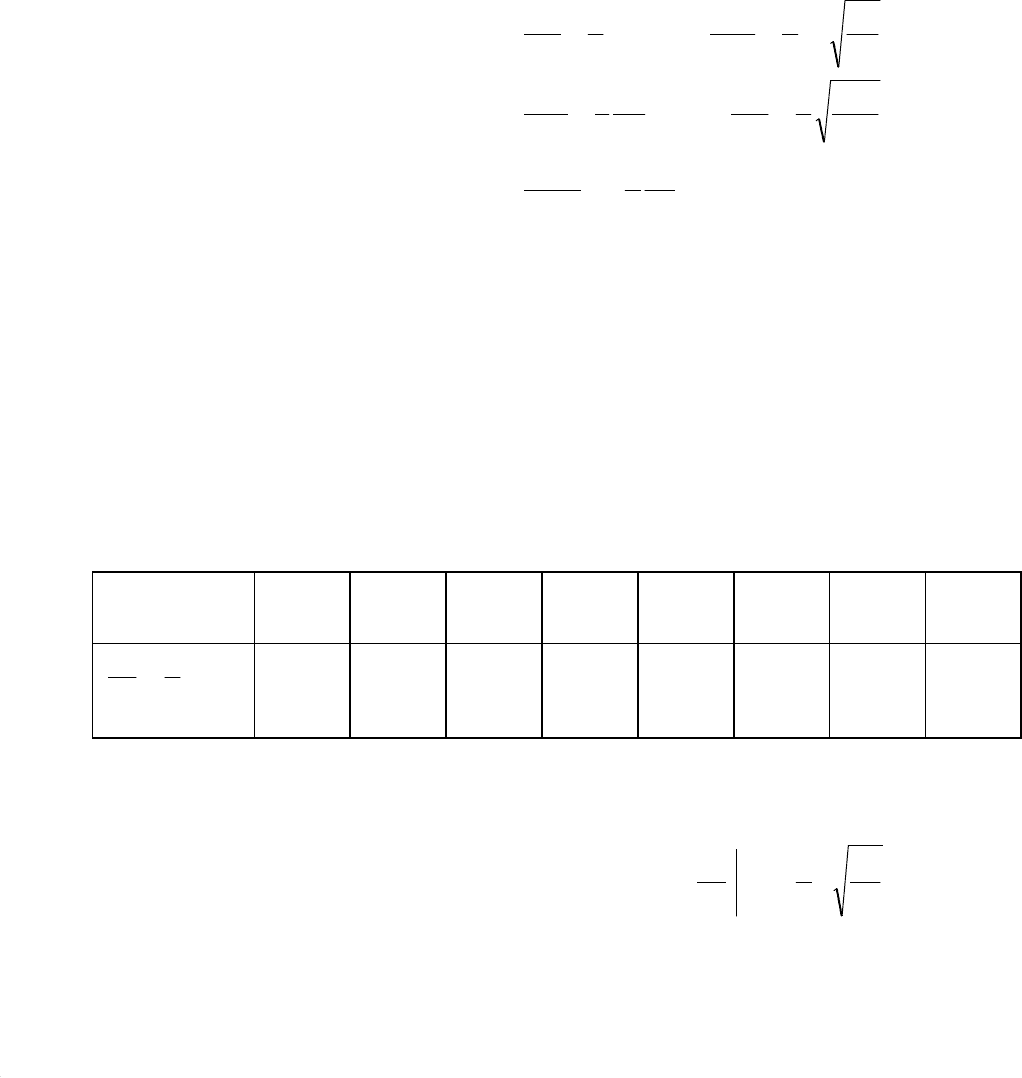
[ ]
)(
4
1
,)()(
2
1
),(
8
1
),(
4
1
),(
2
1
''
2
''''
2
3
3
''
2
2
'
ηηϕ
ψ
ηηϕηϕ
ν
ψ
ηϕ
ν
ψ
ηϕ
ν
ψ
ηϕ
ψ
x
u
yx
x
u
xx
u
y
x
u
u
y
u
y
∞
∞∞
∞
∞∞
−=
∂∂
∂
−=
∂
∂
=
∂
∂
=
∂
∂
=
∂
∂
и подставляя в (15.13), (15.14), придем к задаче
.2
,00,0
,0
'
'
'''''
∞→→
===
=+
ηϕ
ηϕϕ
ϕϕϕ
при
при (15.16)
Эта задача решается численно, и получаются следующие результаты:
η
0 0,1 0,4 0,7 1,0 1,5 2,0 2,8
)(
2
1
'
ηϕ=
∞
u
u
0 0,0664 0,265 0,456 0,63 0,846 0,956 0,998
Из найденного решения можно вычислить напряжение трения на поверхности пластины:
.)0(
4
1
)(
''
3
0
ϕ
ν
µµτ
x
u
y
u
y
w
∞
=
=
∂
∂
=
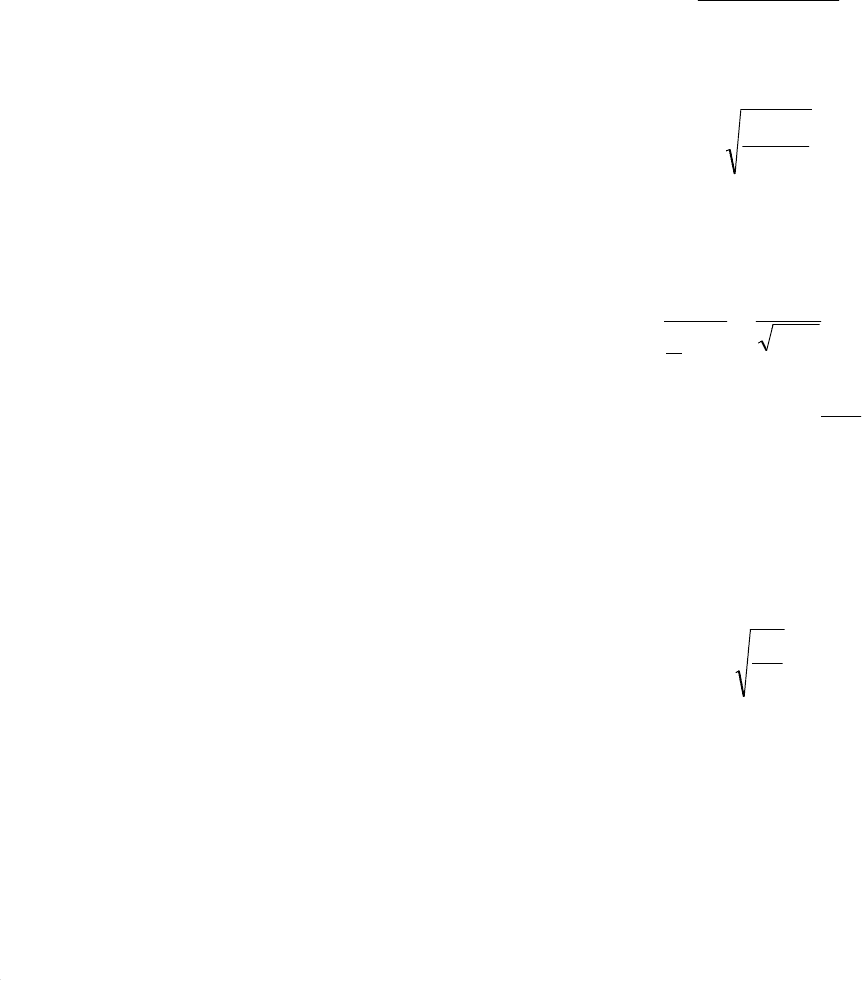
Определяя приближенно по таблице
,328,1
1,0
)0()1,0(
)0(
''
''
=
−
≈
ϕϕ
ϕ
получаем формулу Блазиуса распределения трения по поверхности пластины:
x
u
w
3
332,0
∞
=
ρµ
τ . (15.17)
Эта формула хорошо совпадает с опытными данными, исключая области, близкие к концам
пластины. Вводя так называемый местный коэффициент сопротивления трения
f
C
в силу (15.17),
получим:
,
Re
664,0
2
1
2
x
u
C
w
f
==
∞
ρ
τ
(15.18)
где через xRe обозначено местное число Рейнольдса
ν
xu
x
∞
=Re
.
Сравнение теоретических значений скоростей с экспериментальными данными показало хорошее
совпадение в различных сечениях, за исключением области вблизи носика.
Понятие толщины пограничного слоя (п.с.) весьма условно. Если под толщиной п.с. понимать
такое размерное расстояние
δ
=
y
от стенки, где продольная размерная скорость u
, например, на 1 %
отличается от скорости внешнего потока
∞
u , то по табличному решению
∞
≈
u
xν
δ 0,5 . (15.19)
Если повышать точность совпадения u и
∞
u
, то толщина будет соответственно увеличиваться.
Так, если потребовать, чтобы отклонение не превышало 0,2 %, то коэффици
ент 5.0 в предыдущей
формуле заменится на 5,8 и т.д.
Однако для определения пристеночной области, где необходимо
учитывать силы трения, принятой условности вполне достаточно.
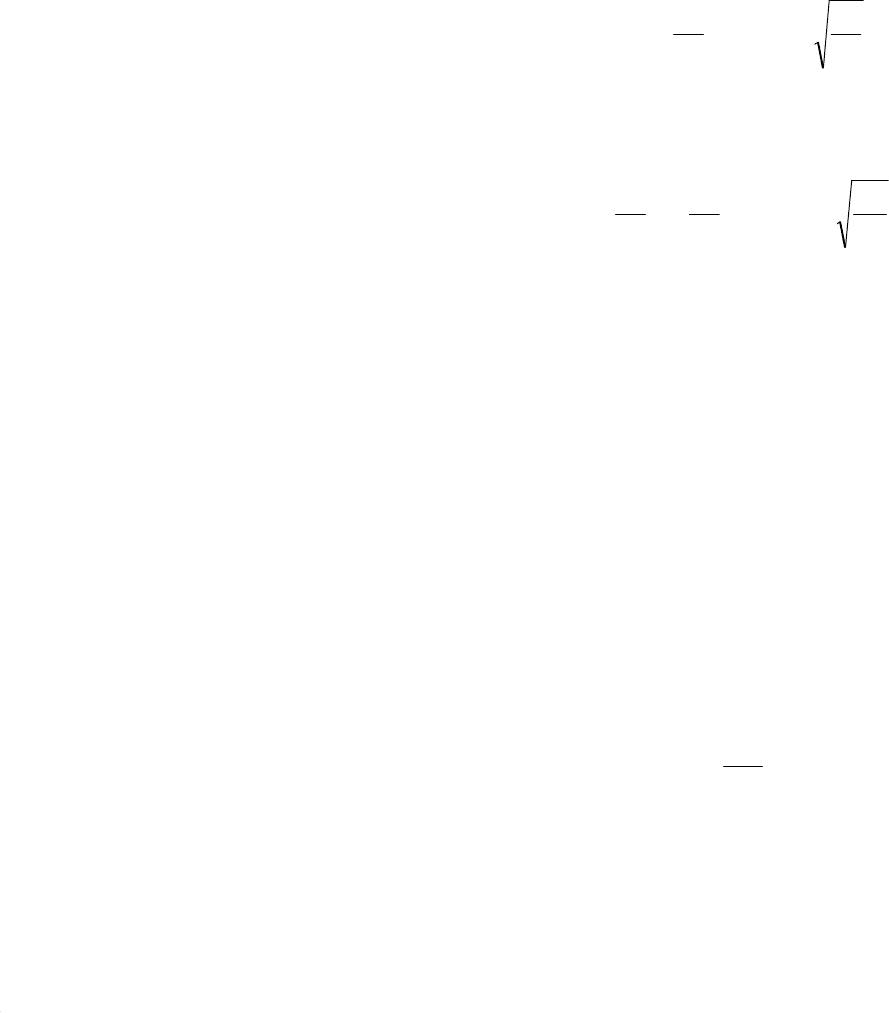
Для того чтобы избежать такой неопределенности, вводятся условные понятия тол
щины
пограничного слоя: толщина вытеснения
*
δ , равная в случае пластины
∫
∞
∞∞
=−=
0
*
721,1)1(
u
x
dy
u
u ν
δ
, (15.20)
и толщина потери импульса
∫
∞
∞∞∞
=−=
0
.
**
664,0)1(
u
x
dy
u
u
u
u
ν
δ . (15.21)
Приведенные определения не имеют той наглядности, как представле
ние о толщине слоя
(
***
5.73 δδδ ≈≈ ), зато слабо зависят от неточности учета совпадения u и
∞
u при больших y
. Ряд
приближенных методов расчета пограничного слоя основан на уравнениях относительно
*
δ и
**
δ
,
которые выводятся из уравнений движения.
§16. Обтекание шара при малых значениях числа Рейнольдса. Формула Стокса
Классическая задача Стокса о медленном стационарном обтекании шара заключается в том, что
основное значение придается силам трения и давлений, а инерционными членами пренебрегают.
Рассмотрим задачу о течении вязкой жидкости, вызываемом движением сферы радиуса а
,
перемещающейся прямолинейно и равномерно со скоростью
∞
V . Очевидно, что эта задача эквива
лентна
задаче об обтекании сферы радиуса а
потоком вязкой жидкости, имеющим на бесконечности
постоянную по величине и направлению скорость
∞
V .
За число Рейнольдса берут
ν
aV
∞
=Re
. (16.1)
Если число Re достаточно мало,
т.е. либо скорость движения сферы достаточно мала, либо радиус
сферы очень мал, то можно пренебречь инерционными членами в уравнениях движе
ния. Так и поступил
Стокс, впервые решивший в 1851 г. задачу о движении сферы в вязкой жидкости. Отбрасы
вая в
стационарных уравнениях Навье-Стокса инерционные члены и по
лагая, что внешние силы отсутствуют,
получим
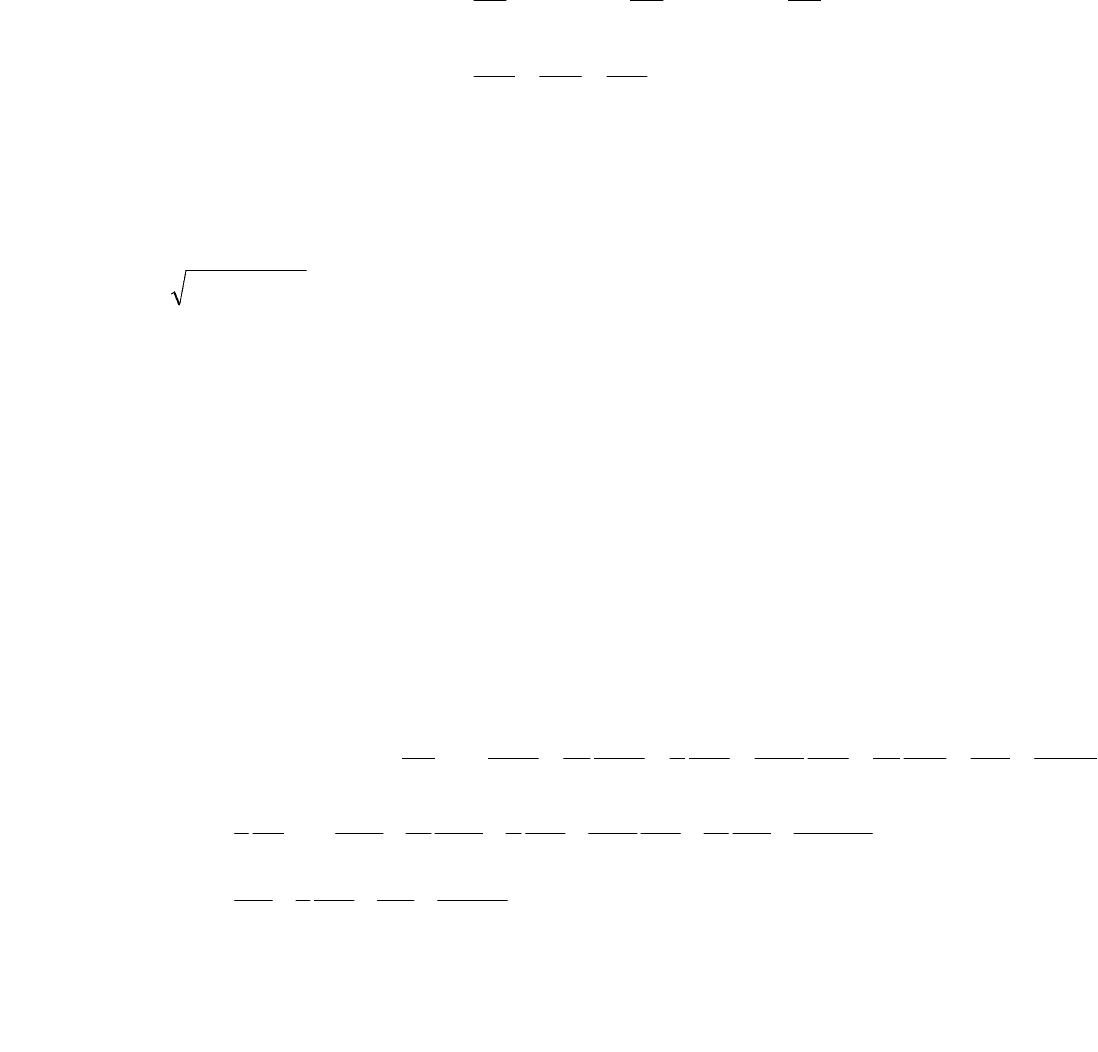
.0
,,,
=
∂
∂
+
∂
∂
+
∂
∂
∆=
∂
∂
∆=
∂
∂
∆=
∂
∂
z
V
y
V
x
V
V
z
p
V
y
p
V
x
p
z
y
x
zyx
µµµ
(16.2)
Здесь
∆
- оператор Лапласа.
Рассматриваем обтекание покоящейся сферы, центр которой находится в начале координат.
На
поверхности тела выполняется условие прилипания
,,0 arприVVV
zyx
====
(16.3)
где
222
zyxr ++= .
Полагаем, что поток на бесконечности параллелен оси Ox, т.е.
∞→→→→
∞
rприVVVV
zyx
0,0, . (16.4)
Введем сферическую систему координат
λ
θ
,,r (угол
θ
отсчитывается от оси Ox
). Вследствие
симметрии движения относительно оси Ox имеем:
).,(,0),,(),,( θθθ
λθθ
rppVrVVrVV
rr
====
Поэтому уравнения (16.2) в сферической системе координат примут вид:
),
22
221
(
22222
2
22
2
θ
θ
θ
θθ
θ
θ
µ V
r
ctg
r
V
V
r
V
r
ctg
r
V
r
V
rr
V
r
p
r
rrrrr
−−
∂
∂
−
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
=
∂
∂
22
2222222
1122
(),
21
0,
r
rr
VVVVV
Vpctg
rrrrrrrrSin
VVctg
VV
rrrr
θθθθθ
θθ
θ
µ
θθθθθ
θ
θ
∂∂∂∂
∂∂
=++++−
∂∂∂∂∂∂
∂
∂
+++=
∂∂
(16.5)
