Презентация - Андреев В.К. Механика жидкости и газа
Подождите немного. Документ загружается.

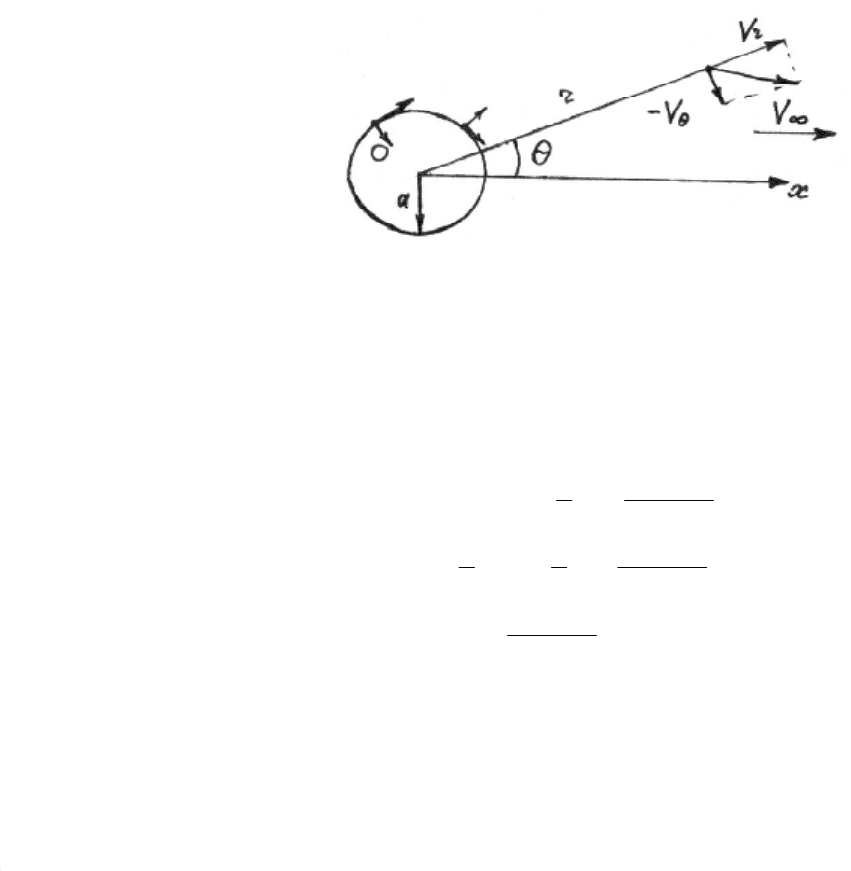
граничные условия
.0),(,0),( == θθ
θ
aVaV
r
(16.6)
∞→−→→
∞∞
rприVVVV
r
θθ
θ
sin,cos
. (16.7)
Рис.16.1
Учитывая вид граничных условий, будем искать решение уравнений (16
.5) в форме
θµθθ
θ
cos)(,sin)(,cos)( rhprgVrfV
r
=−== .
Тогда для трех функций f,g и h получим три обыкновенных дифференциальных уравнения:
.0
)(2
,
)(22
,
)(4
2
'
2
'''
2
''''
=
−
+
−
++=
−
−+=
r
gf
f
r
gf
g
r
g
r
h
r
gf
f
r
fh
(16.8)

Из (16.6) и (16.7) вытекают следующие граничные условия:
∞∞
=∞=∞== VgVfagaf )(,)(,0)(,0)( . (16.9)
Найдем решение системы (16.8). Из третьего уравнения следует:
.
2
1
'
frfg += (16.10)
Из второго уравнения находим h:
'''2'''
23
2
1
frfrfh ++= . (16.11)
Наконец из первого уравнения получаем уравнение для определения f:
.0888
''''''23
=−++ frffrfr
IV
16.12)
Частные решения этого уравнения имеют вид
k
rf =
, где
k
определяются из уравнения чет
вертой
степени.
.3,1,2,0..,0)3)(1)(2(
08)1(8)2)(1(8)3)(2)(1(
−=−====++−
=−−+−−+−−−
kkkkетkkkk
илиkkkkkkkkkk
Таким образом, общее решение уравнения (16.12) имеет вид:
.
2
3
rDC
r
B
r
A
f +++=

После этого из (16.10) и (16.11) находим g и h:
.10,2
2
2
2
2
3
rD
r
B
hrDC
r
B
r
A
g +=+++−=
Постоянные А,В,С и D определяются из граничных условий (16.9):
.
2
1
,
2
3
,,0
3
aVAaVBVCD
∞∞∞
=−===
В результате нашли решение задачи :
.cos
2
3
,
4
1
2
3
1sin
,
2
1
2
3
1cos
2
3
3
3
3
θµ
θ
θ
θ
r
aV
p
r
a
r
a
VV
r
a
r
a
VV
r
∞
∞
∞
−=
+−−=
+−=
(16.13)
Найдем силу, с которой поток воздействует
на сферу. Вычислим напряжения, действующие на
элементы сферы:
).
1
(,2
r
V
r
VV
r
p
r
V
pp
r
r
r
rr
θθ
θ
θ
µµ −
∂
∂
+
∂
∂
=
∂
∂
+−=

На поверхности сферы 0==
θ
VV
r
, а следовательно, .0,0 =
∂
∂
=
∂
∂
θθ
θ
VV
r
Из последнего уравнения
системы
(16.5) получаем ,0=
∂
∂
=ar
r
r
V
поэтому предыдущие формулы для точек сферы существенно упрощаются:
.sin
2
3
,cos
2
3
θ
µ
µθ
µ
θ
θ
a
V
r
V
p
a
V
pp
rrr
∞∞
−=
∂
∂
==−=
(Направления этих сил показаны на рис.16.1.)
Равнодействующая всех сил совпадает с направлением потока на бесконечности и находится по формуле
,sin3sin2)sincos()sincos(
0
2
0
∫∫∫∫
∞
=−=−=
ππ
θθ
θθµπθθπθθθθ daVdappdSppW
rrr
S
rrrx
.6 aVW
x ∞
= µπ
(16.14)
Это выражение силы сопротивления называют формулой Стокса. Данная сила отлична от нуля (парадокс
Даламбера не имеет места).

Лекция 21
§17. Основные понятия теории устойчивости
Рассмотрим систему дифференциальных уравнений
(,)
xftx
r
rr
&
(17.1)
с начальным условием
00
()
xtx
r
.
Пусть
()
xt
r
r
- решение системы (17.1), определенное при
0
tt
.
Определение. Решение
()
xt
r
r
системы (17.1) называется
устойчивым
по Ляпунову, если для любого
0
существует
0
такое, что как только
00
|()|
tx
r
r
, где
0
x
r
-заданный вектор, то
|()()|
tt
r
r
, для всех
0
tt
, где
()
t
r
-решение системы (17.1) с начальным условием
00
()
tx
r
r
. Если, кроме
того,
lim|()()|0
t
tt
r
r
, то решение
()
xt
r
r
называется
асимптотически
у
стойчивым.

Однородная линейная система дифференциальных уравнений с постоянными коэффициентами.
Устойчивость решения
0
x
r
Рассмотрим линейную однородную систему из n дифференциальных уравнений
,
xAx
rr
&
(17.2)
Пусть
kkk
i
-собственные значения матрицы
A
(1,..,, )
kmmn
.
Лемма 1. Если действительные части всех собственных чисел матрицы
A
-
отрицательны, то есть
Re0
kk
, то для любого решения
()
xt
r
r
системы (17.2) существует
0
,
0
R
, такие, что выпол
нено
|()|
t
tRe
r
при всех
0
t
.
Лемма 2. Если все действительные части всех собственных чисел матрицы
A
- от
рицательны, то для
любого решения системы (17.2)
0
(,)
xtx
rr
r
, удовлетворяющего начальному условию
00
(0,)
xx
rr
r
существуют
числа
0, 0
r
, такие, что при
0
t
справедливо
00
|(,)|||
t
txrxe
rr
r
.
Теорема. Если все действительные части всех собственных чисел матрицы
A
-
отрицательны, то
положение равновесия
0
x
r
(решение
0
x
r
) является асимптотически устойчивым.
Ле
мма Ляпунова
Рассмотрим нормальную систему дифференциальных уравнений
(,).
xftx
r
rr
&
(17.3)
Лемма Ляпунова. Пусть определена область
0
:||,
Dxrtt
r
. В области
D
для системы (17.3
) выполнены
все требования существования и единственности и, кроме того, при
||
xr
r
существует функция
()0
Vx
r
,
причем
0
V
только в точке
0
x
r
.
1
()
VxC
r
и
1
0
n
i
i
i
V
f
x
в
D
,
1
(,..,)
n
fff
r
.
Тогда решение
0
x
r
устойчиво по Ляпунову. Если, кроме того,
()0
Wx
r
, определенная в
D
функция,
0
W
только при
0
x
r
и
1
()
n
i
i
i
V
fWx
x
r
,
тогда решение
0
x
r
асимптотически устойчиво.

Теорема Ляпунова
Пусть
0
x
r
- положение равновесия нормальной системы дифференциальных уравнений
(,),
xftx
r
rr
&
(17.4)
правая часть которой удовлетворяет условиям теоремы существования и единственно
сти и
имеет вид
(,)()(,),
ftxAtxFtx
r
r
rr
где
()
At
- матрица
(,0)
(),
i
j
ft
At
x
причем
||0
|(,)|
lim0, (,0)0.
||
x
Ftx
Ft
x
r
r
r
r
Линейная однородная система дифференциальных уравнений
()
xAtx
rr
&
называется
первым
приближением
или
линеаризацией
исходной системы уравнений (17.4).
Рассмотрим частный случай, когда матрица
()
At
- постоянна.
Теорема Ляпунова.
Пусть дана нормальная система дифференциальных уравнений
(,), (,0)0,
xAxFtxFt
rr
rrr
&
(17.5)
где
A
- постоянная матрица. Собственные значения матрицы
A
имеют отрицательные
действительные части. Для вектор-функции
()
Ft
r
в окрестности точки
0
x
r
выполнено
1
|(,)|||,
FtxMx
r
rr
где
0, 0
M
- постоянные. Тогда положение равновесия
0
x
r
системы
уравнений (17.5) асимптотически у
стойчиво.

Рассмотрим 2 системы уравнений
(,),
xftx
r
rr
&
………………..……………….(17.6
)
(,)(,),
xftxRtx
r
r
rrr
&
……………………………(17.7
)
правые части которых удовлетворяют теоремам существования и
единственности на некотором открытом множестве
G
. Система (17.7
)
называется возмущенной по отношению к системе (17.6).
Определение. Решение
0
x
r
системы уравнений (17.6
) называется
устойчивым по отношению к постоянно действующим возмущениям
,
если для любого
0
существуют
12
0, 0
, такие что для любой
функции
(,)
Rtx
r
r
и для любой точки
0
x
r
, подчиняющихся условиям
1002
|(,)| ((,), ), ||
RtxtxGttx
r
rrr
,
решение
()
t
r
системы уравнений (17.7)
, удовлетворяющее начальному
усл
овию
00
()
tx
r
r
, подчиняется неравенству
|()|
t
r
при всех
0
tt
.

Лекция 22
Постановка задачи о гидродинамической устойчивости
Ламинарные течения –
гладкие течения, плавно
эволюционирующие под действием внешних условий. Траектории
частиц, линии тока, поля ско
ростей и давлений в таких движениях
имеют определенный «регулярный» характер.
Ф
орма движения, при котором частицы жидкости или газа
совершают
неупорядоченные, хаотичные движения по сложным
траекториям , а скорость, температура, давление и
плотность среды
испытывают хаотичные флуктуации. называется
турбулентным
течением
. Турбулентные течения отличаются от ламинарных
интенсивным перемешиванием, теплообменом.
Re
ud
- число Рейнольдса
u
- скорость,
d
- диаметр трубы,
- коэффициент вязкости
Турбулентная жидкость
Условия Рейнольдса:
1.
, const;
aaa
2.
, const;
afafa
3.
;
ii
xx
ff
4.
;
fgfg
5.
fgfg
, где
g
может принимать значения
1,,
ghh
. Тогда
условие 5) эквивалентно трем условиям: 5а)
ff
, 5б)
fhfh
, 5в)
0
fh
.
Все эти условия означают, что оператор осреднения есть
- линейный:
, ,const
afbhafbhab
,
- непрерывный:
limlim
nn
nn
ff
,
- проектор:
ff
.
