Презентация - Андреев В.К. Механика жидкости и газа

Подождите немного. Документ загружается.

Далее используем метод нормальных мод.

Эта процедура сводит задачу к

системе обыкновенных дифференциальных уравнений, решая которую по

лучим две

моды, для которых комплексный декремент

1/2

1122121212

121212

()()

()

UUUUkg



























где

222



- полное волновое число.

Обе моды нейтрально устойчивы, если

2121

)()(

UUgk −ρρα≥ρ−ρ .

Одна мода является асимптотически устойчивой, другая – неустойчивой, если

2121

)()(

UUgk −ρρα<ρ−ρ .

Это необходимое и достаточное условие устойчивости мод с волно

выми

числами

. Таким образом, течение всегда неустойчиво (по отноше

нию к коротким

волнам, т.е. при больших

), если

≠

§20. Приложения теории

Поверхностные гравитационные волны

Условия





соответствуют

модели поверхностных

гравитационных волн на глу

бокой воде. Эти волны являются устойчивыми и имеют

фазовую скорость .)

2/1

kgki ±=σ=σ

Внутренние гравитационные волны

Когда основное течение является состоянием покоя

, имеем

(

)

.)/()(

2/1

1212

ρ+ρρ−ρ±=σ gk

Состояние неустойчиво, когда

. Если

, то состояние у

стойчиво, а

нормальная мода пред

ставляет собой волну, распространяющуюся с фазовой

скоростью

(

)

2/1

12121

)(

/)( ρ+ρρ−ρ=σ kg .

Эти волны представляют собой

специальный случай внутренних гравитационных волн, которые мо

гут

распространяться внутри стратифицированной жидкости вдали от какой-

либо

границы.

Неустойчивость Релея

—Тейлора

Если жидкая система в целом имеет направленное вверх вертикальное

ускорение величины

Тогда, решая задачу с нормальными модами, имеем

(

)

,)/()(

2/1

1212

ρ+ρρ−ρ

′

±=σ gk

′

где g

′

— кажущееся гравитационное или результирующее вер

тикальное ускорение

системы. Неустойчивость имеет место, если

′

, т.е. результи

рующее ускорение

направлено от легкой жидкости к тяжелой. Эта не

устойчивость была названа

неустойчивостью Р

лея

Тейлора

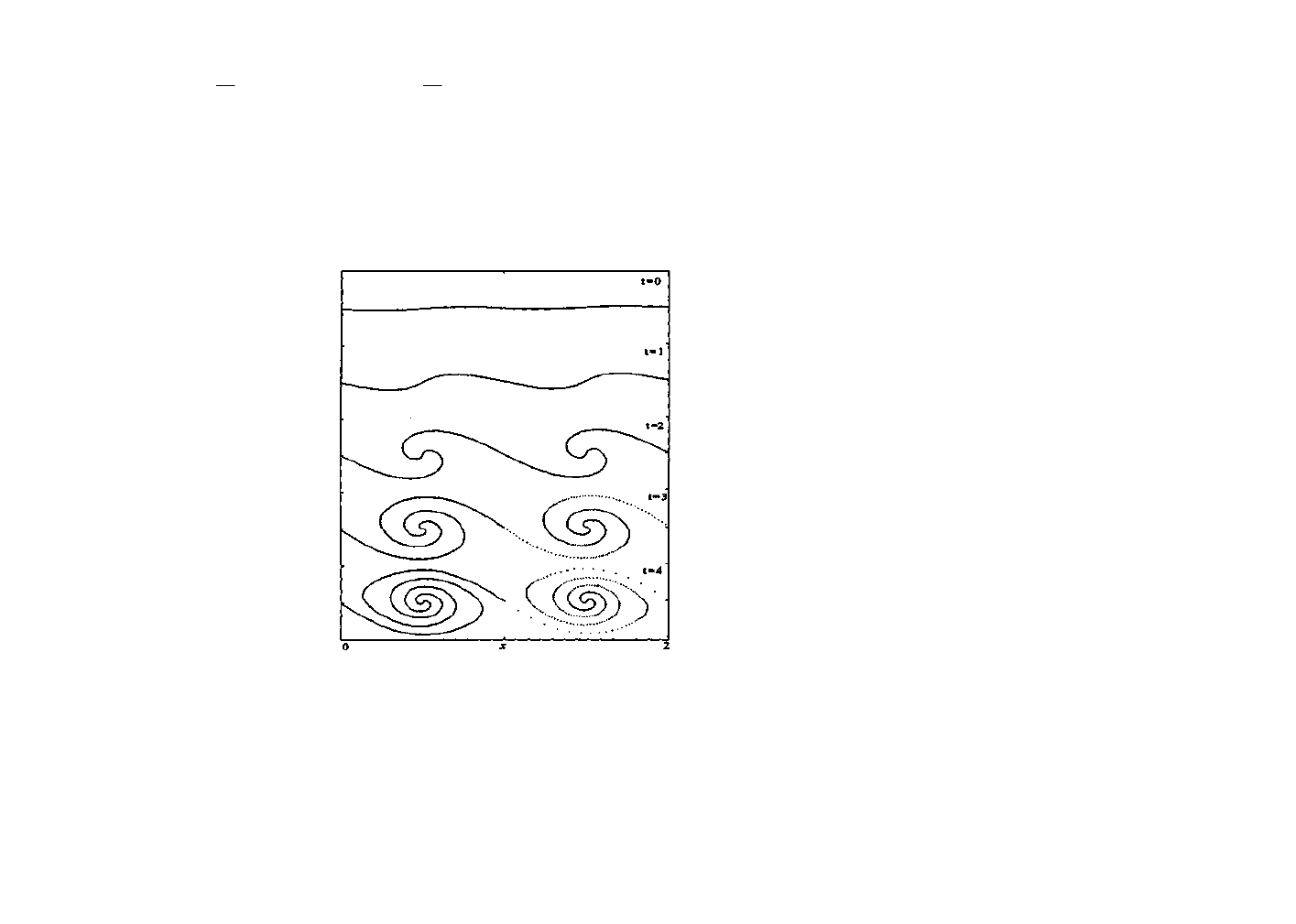
Сдвиговая неустойчивость

В присутствии вихревого слоя в однородной жидкости (

2121

≠

)

).(

)(

2121

UUUUi −α±+α=σ

На рисунке показана схема сворачивания вихревого слоя вследствие сильно-

нелинейного роста двумерного возмущения.

Сдвиговый слой неустойчив по

отношению к волнам с длинами много большими толщины слоя.

Для реального сдвигового слоя конечной толщины, называемого свободным

сдвиговым слоем или слоем смешения короткие волны являются устойчивыми.

Лекция 25

§21. Конвекция Релея-Бенара

Тепловая конвекция

Имеется бесконечный слой жидкости, ограниченный неподвижными горизонта

льными

плоскостями

zzd



, температура которых поддерживается

постоянной и равной



соответственно.

**0**00***

0, , , 0,

UzPpgzzzd





















где

()/





- средняя плотность,



- коэффициент теплового

расширения

жидкости. Если



достаточно мало, то вязкость и т

епловая диффузия будут

стабилизировать течение, даже если



, (

т. е. горячая жидкость располагается ниже

более холодной и, следовательно, более плотной жидкости), но если



превосходит

некоторое критическое значение, то возникает «опрокидывающая» неустойчивость.

Конвекцию в тонком слое моделируют

при помощи уравнений движения, энергии и

состояния для

жидкости Буссинеска

(

уравнение состояния жидкости имеет вид

*0*0

(1())



)

****0*

***

grad grad (),

div 0,

grad ,

uugzgku

rrr

































(21.1

)

. Уравнения (21.1) называются

уравнениями Буссинеска.

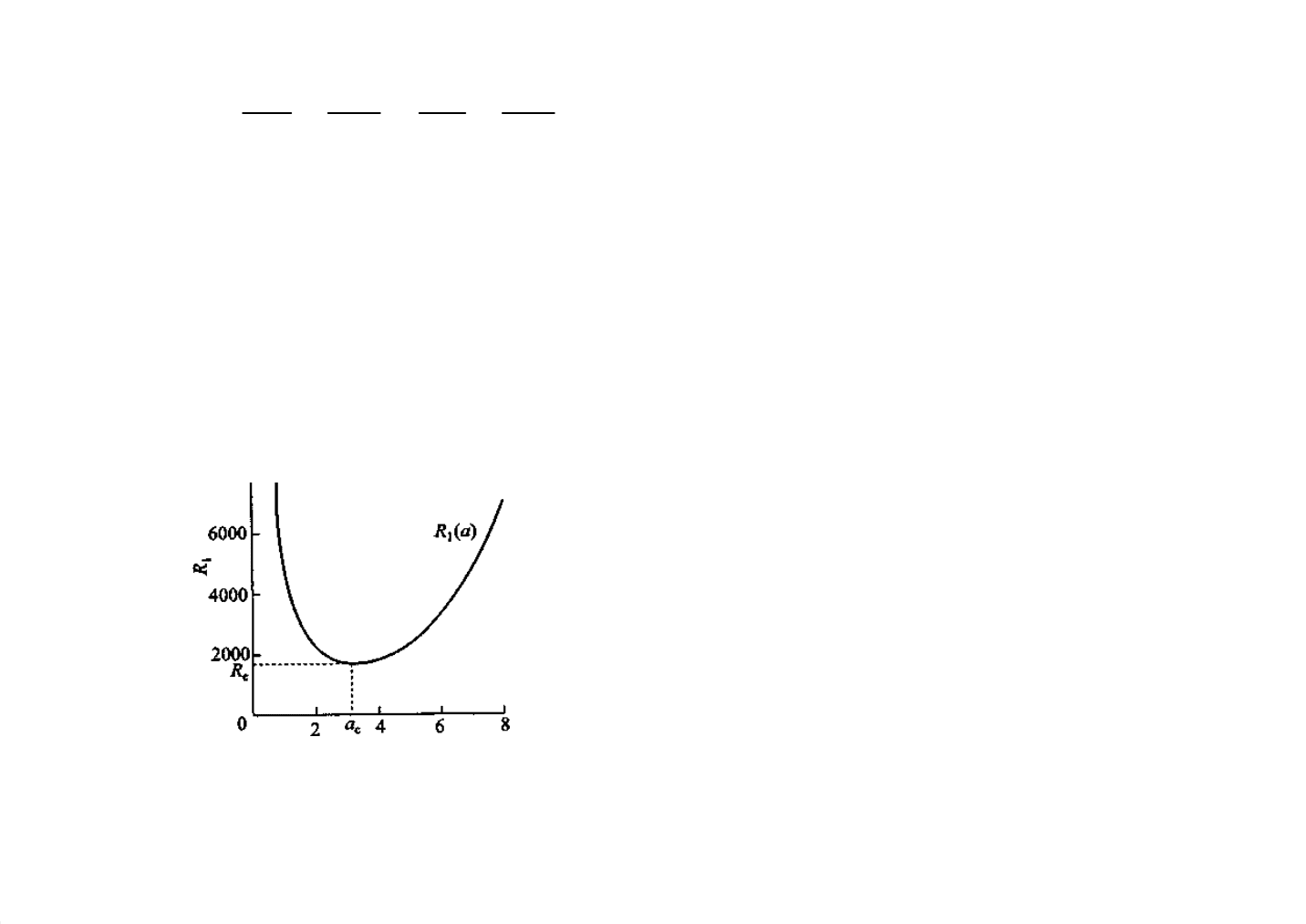
На неподвижной твердой поверхности задается граничное условие



. Если имеется

свободная поверхность, задаваемая уравнением

const



, то считаем ее горизонтальной и

стационарной с нулевым

сдвиговым напряжением,

т. е.

****

uwvw

zxzy







Линеаризованная задача

Пусть

***************

(,), ()(,), ()(,).

uuxtzxtpPzpxt





rrrrr

Линеаризуем уравнения Буссинеска (21.1) для малых возмущений. В безразмерных

переменных

*****0

/, /, /, /, /,

xxdttduuddppd

rrr







получим

задачу, со следующими безразмерными параметрами:

Ra/



число Релея

Pr/



число Прандтля.

Для рассматриваемых задач справедлив

принцип

смены устойчивости

: если

Ra0



, то

Re()0



и течение

устойчиво, если же

Ra>0

, то

Im()0



Нейтральная

кривая

определяется соотношением



Такой тип неустойчивости называют

конвективной

неустойчивостью

, или неустойчивостью Релея-Бенара.

Лекция 26

§22. Устойчивость параллельных течений. Теорема Сквайра.

Идеальная жидкость

Для заданного плоско-параллельного течения характерная скорость и длина -

соответственно. Безразмерные переменные

****

/, /, /, /.

xxLtVtLuuVppV



rrr

Уравнения Эйлера для идеальной жидкости и уравнение неразрывности

безразмерной форме примут вид

uup









а граничные условия при

zzzz



запишутся в следующей форме



Основное течение в канале зададим в виде

(), const ().

UUziPzzz



Задача на собственные значения

()0, ()0,

()0, 0.

iUcuUwipiUcvip

iUcwpiuivw









(22.5)

(,)0 (,).

wxtzzz



(22.6

)

Для решения задачи (22.5), (22.6) используем преобразование Сквай

ра

221/2

(), ()/, /

uuvpp



%%%

. В результате получим преобразованную задачу

на собственные значения в специальном случае

двумерных волновых мод, когда



; отсюда следует соотношение на собственные зна

чения для заданного

основного течения имеет вид

(,)0



рехмерная мода представляет собой волну, распространяющуюся наклонно к плоскости основного

течения, и только компонента осн

овного течения в направлении движения волны влияет на рост волны,

так что скорость про

порциональна этой компоненте. Это означает, что каждой неустойчивой трехмерной

моде соответствует более неустойчивая двумерная мода. Этот результат – теорема Сквайра.

Тре

хмерная задача может быть преобразована в задачу для двумерной моды и можно ограничиться

решением задачи на собственные значения только для двумерных мод.

Итак, положим

,0,uvw

ψψ

′

∂∂

′′′

===−

∂∂

и используем нормальные моды вида

i()

(,,)()e.

xct

xztz

ψφ

−

′

= Следовательно,

uwi

==−αφ

⇒

().

dUd

pUc

dzdz

=φ−−

Задача устойчивости Релея

()()0,

UcU

′′′′

−φ−αφ−φ=

- уравнение устойчивости Релея,

()0

при ,,

zzzz

φ==

В задачу на собственные значения

вход

ит только во второй степени. Таким образом, если величины

являются собственной функцией и соответствую

щим собственным значением, для данного значения

, то они также являются решением и для отрицательного значения

−α

. Это свойств

о связано с

обратимостью задачи по времени и пространству.

Общие свойства задачи устойчивости Релея

Необходимым условием для неустойчивости является наличие

точки перегиба в профиле основного

течения (условие Релея).

Условие Фьертофта: необходимым условием неустойчивости является условие

()0

UUU

′′

−<

где

либо в поле течения, где

является точкой, в которой

()0

′′

()

UUz

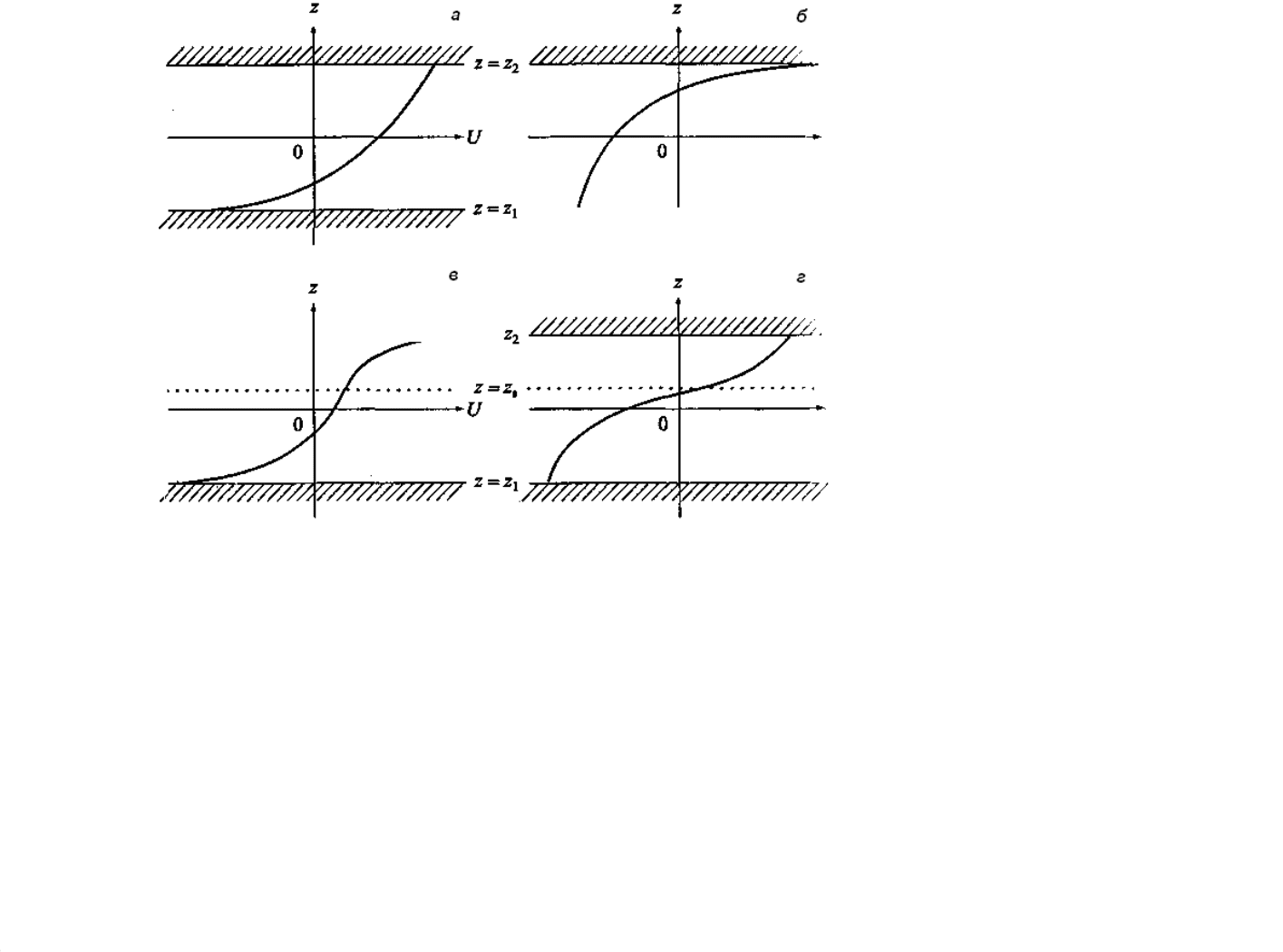
Некоторые примеры течений, удовлетворяющие необходимому

условию

неустойчивости Релея–Фьёртофта. (а) Устойчиво, потому что везде

′′

; (б

)

Устойчиво, потому что

′′

в каждой точке; (в) Устойчиво, потому что

()0

′′

но

()0

UUU

′′

−≥

; (г) Течение возможно неустойчиво, так как

()0

′′

()0

UUU

′′

−≤

На практике, условия Релея–Фьёртофта часто являются необходи

мыми и

достаточными для неустойчивости.

Лекция 27

Характеристики устойчивости некоторых течений идеальной жидкости

Пример1.

Устойчивость плоского течения Куэтта.

Если

()

Uzz

при

−<<

тогда

уравнение устойчивости Релея принимает вид

()()0,

′′

−φ−αφ=

поэтому

′′

φ−αφ=

там, где

≠

Дискрет

ный спектр представляет собой пустое множество и плоское

течение Куэтта идеальной жидкости является устойчивым. Однако условия

задачи

могут удовлетворяться на кусках при помощи непрерывной функции

с разрывной

производной на критическом слое

для всех

таких, что

−<<

и для всех

Собственная функция, пропорциональна

где

sh(1)sh(1)

для 1zc,

()

sh(1)sh(1)

для z1.

zcc

α+α+−≤≤



φ=



α−α−≤≤



Это дает непрерывный спектр.

Пример 2

Неустойчивость Кельвцна-Гелъмголъца.

Выберем в качестве

скорости

основного течения

для z0,

()

для z0,





−<



, тогда

для z0,

()

для z0,

−







при некоторых постоянных

. Для разрывной функции

()

имеем

(())0 при

UcUzz

′′

−φ−φ==

. В нашем случае

. Решая задачу относительно

получим

=−

Поэтому

=±

и относительная скорость роста

α=±α

дает одну

экспоненциально затухающую и

одну возрастающую моду для каждого значения

волнового числа. Следовательно, течение является неустой

чивым для волн с любой

длиной волны.

Вязкая жидкость

Устойчивость плоско-параллельных течений вязкой жидкости

Возьмем снова

(),

UUziPpGx

==− при

zzz

≤≤

для основного течения в канале с

некоторым постоянным градиентом давления с обратным знаком

В задаче на собственные значения,

определяется через U, z

, z

221/2

(), Re

α+βα

Задача Орра-Зоммерфельда

IV242

2i[()()],

RUcU

′′′′′′

φ−αφ+αφ=α−φ−αφ−φ

()()0

при ,.

zzzzz

′

φ=φ==

Ее решение для собственных значений может быть записано в форме

(,,Re)0

αα=

Характеристики устойчивости некоторых течений вязкой жи

дкости

Если для данного профиля скоростей основного течения, (1)

некоторая мода

неустойчива и собственное значение равно с

∞

для идеальной жидкости (

Re0

), то

собственное значение с для вязкой жидкости стремится к с

∞

при

→∞

, но (2)

если эта мода устойчива для идеальной жидкости, то с

∞

может не быть пределом

какого-либо собственного зна

чения для маловязкой жидкости. Если данное

течение устойчиво при

=∞

(т. е. устойчиво для всех мод, когд

а жидкость

является идеальной), то оно может оказаться неустойчивым, имея, по

крайней

мере, одну моду с

1/3

(Re)

−

при

→∞

. Таким об

разом, наличие вязкости

может привести к неустойчивости течения, которое было устой

чиво в идеальной

жидкости; также вязкость может сделать более неустойчивым течение, кото

рое

неустойчиво и в идеальной жидкости.