Прохоров В.Т. Особенности защиты человека от воздействия низких температур
Подождите немного. Документ загружается.


391
( )
=
+
∑
∫
=
−
iip
i
ip
n
i
l
l
iip
i
i
dx
a
x
xNM
a
i
i
ϕ
µ
sin0,
λ
1
1
.
µ
sin
λ
~
1
22
1
1
∑
∫
=
−
+=
n
i
l
l
iip
i
ip
i
i
ipp
i
i
dx
a
x
a
MA
ϕ
Отсюда:
( )
iip
i
ip
n
i
l
l
ip
i
i
iip
i
ip
n
i
l
l
iip
i
i
p
dx
a
x
M
a
dx
a
x
xNM
a
A
i
i
i
i
+
+
=
∑
∫
∑
∫
=
=
−
−
ϕ
ϕ
µ
sin
λ
µ
sin0,
λ
~
2
1
2
1
1
1
1
. (5.16)
Таким образом, решение задачи (5.1) - (5.5):
( )
( )
+−++=
∑
∞
=
ik
i
ik
k
k
ikkiiiii
a
x
tMABxAtxT
ϕ
µ
sinµexp
~
,
2
1
1
, (5.17)
в котором коэффициенты
kikii
AMBA
1
~
,,,
определяются по форму-
лам (5.6), (5.14), (5.15). Ряд (5.17) при
0
=
t
сходится абсолютно и
равномерно по
],[
1 iii
llx
−
∈
как ряд Фурье гладкой функции. В силу
(5.13) собственные числа
k
µ
растут не медленнее нулей синуса и
удовлетворяют условию
mk
k
>
µ
для некоторого
0
>
m
и
1
≥
k
. Так
как ряд (5.17) сходится при
0
=
t
, то коэффициенты ряда ограничены,
и, значит, при
0
>
t
справедливо неравенство
( )
)exp(
µ
sinµexp
~
222
1
tkmM
a
x
tMA
ik
i
ik
kikk
−≤
+−
ϕ
.
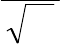
392
Далее, при
0
>
t
ряд
∑
∞
=
−
1
22
)exp(
k
tkmM
сходится, например, по при-
знаку Коши и, следовательно, при
0
>
t
ряд (5.17) сходится абсолют-
но и равномерно по
],[
1 iii
llx
−
∈
.
Отметим, то ряд (5.17) при
0
>
t
сходится очень быстро и для
получения расчетов распределения температуры с довольно высокой
точностью достаточно взять небольшое число членов ряда. В даль-
нейшем доказательство сходимости подобных рядов будем опускать и
ограничимся только ссылкой на работы [115, 116], в которых рассмат-
ривался вопрос сходимости подобных рядов.
Окончательно получаем выражение температуры
i
-го слоя
обуви:
(
)
(
)
( )
+−+++=
=
+
=
∑
∞
=
ik
i
ik
k
k
ikkiiic
ciiii
a
x
tMABxAT
TtxTtx
ϕ
θ
µ
sinµexp
~
,,
2
1
1
(5.18)
5.3 Решение краевой задачи теплопроводности для низа обуви
(многослойной пластины) с граничными условиями 2-4-го рода
При постановке рассмотренной краевой задачи о распределе-
нии температуры подошвы предполагалось, что температура на внеш-
ней части подошвы постоянна и совпадает с температурой окружаю-
щей среды
c
T
. Однако в более общей постановке теплообмен с окру-
жающей средой происходит по закону Ньютона с некоторым коэффи-
циентом теплоотдачи
α
. Иначе говоря, краевая задача сводится к ре-
шению системы:

393
( )
(
)
.,..,1,0,,
,
,
1
2
2
nitlxl
x
txT
atx
t
T
iii
i
ii
ii
i
=><<
∂
∂
=
∂
∂
−
(5.19)
Начальное распределение температуры
(
)
(
)
nixfxT
iiii
,..,1,0,
=
=
. (5.20)
Граничные условия: теплообмен на внешней поверхности с
окружающей средой происходит по закону Ньютона с коэффициентом
теплоотдачи
α
:
(
)
0),(
,
λ =+
∂
∂
tlT
x
tlT
nn
n
nn
n
α
. (5.21)
Внутренняя поверхность подошвы нагревается тепловым по-
током стопы плотности
q
:
(
)
0
,0
λ
1
1
1
=+
∂
∂
q
x
tT
, (5.22)
Между слоями подошвы предполагается идеальный контакт,
который выражается условиями сопряжения на стыках:
(
)
(
)
tTtlT
iii
,0,
11
=
−−
,
( ) ( )
nit
x
T
tl
x
T
i
i
ii
i
i
i
,..2,,0λ,λ
1
1
1
1
=
∂
∂
=
∂
∂
−
−
−
−
. (5.23)
Решение задачи, подобно задаче (5.1) – (5.5), будем искать в
виде
(
)
(
)
(
)
nitxNxRtxT
iiiiii
,...1,,,
=
+
=
, где функция
(
)
ii
xR
является решением краевой задачи стационарной теплопроводности
при соответствующих неоднородных условиях вида (5.21), (5.22) и
условиях сопряжения (5.23). Функция
(
)
txN
ii
,
является решением
нестационарной краевой задачи с однородными краевыми условиями
и неоднородным начальным условием.
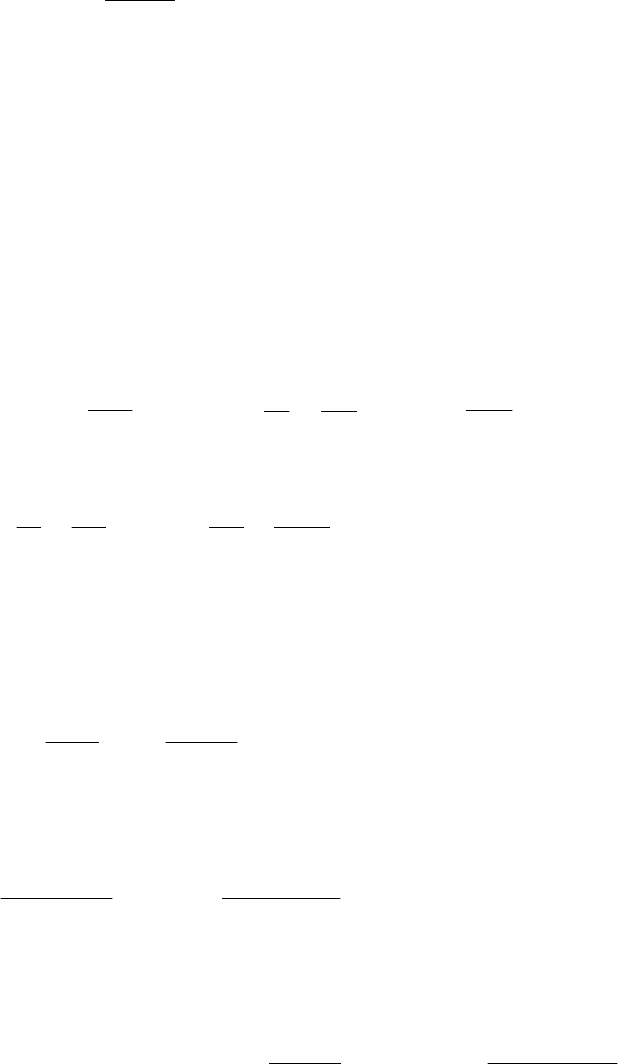
394
Итак, функция
(
)
ii
xR должна быть решением системы:
( )
nix
dx
Rd
i
i
i
,..,1,0
2
2
==
с граничными условиями
(
)
,0)(
=
+
′
nnnn
lRlR
α
λ
(
)
qR −=0λ
/
1
1
,
(
)
),(
111 −−−
=
iiii
lRlR
(
)
)(λλ
1
/
1
/
11 −−−−
=
iiiiii
lRlR
,
n
i
,...
2
=
.
Решением этой системы является niBxAxR
iiiii
,...1,)(
=
+
=
.
Используя граничные условия, находим коэффициенты
i
A
и
i
B
.
n
n
q
A
λ
−
=
,
+=
n
n
n
l
qB
λ
1
α
,
i
i
q
A
λ
−
=
,
,
λ
1
λ
1
λ
1
1
1
−++=
∑
−
=
+
n
ik
kk
k
n
n
i
l
l
qB
α
.
1
,...
1
−
=
n
i
(5.24)
Для нахождения функций ),( txN
ii
решаем систему:
ni
x
N
a
t
N
i
i
i
i
,...1,
2
2
=
∂
∂
=
∂
∂
. (5.25)
Граничные условия на поверхностях:
(
)
0
;0
1
1
=
∂
∂
x
tN
,
(
)
0),(
;
=+
∂
∂
tlN
x
tlN
nn
n
nn
n
αλ
. (5.26)
Условия сопряжения на стыках:
(
)
(
)
tlNtlN
iiii
,,
111 −−−
=
,
( )
(
)
,
,
λ,λ
1
1
1
1
1
i
ii
ii
i
i
i
x
tlN
tl
x
N
∂
∂
=
∂
∂
−
−
−
−
−
(5.27)
.
,...
2
n
i
=
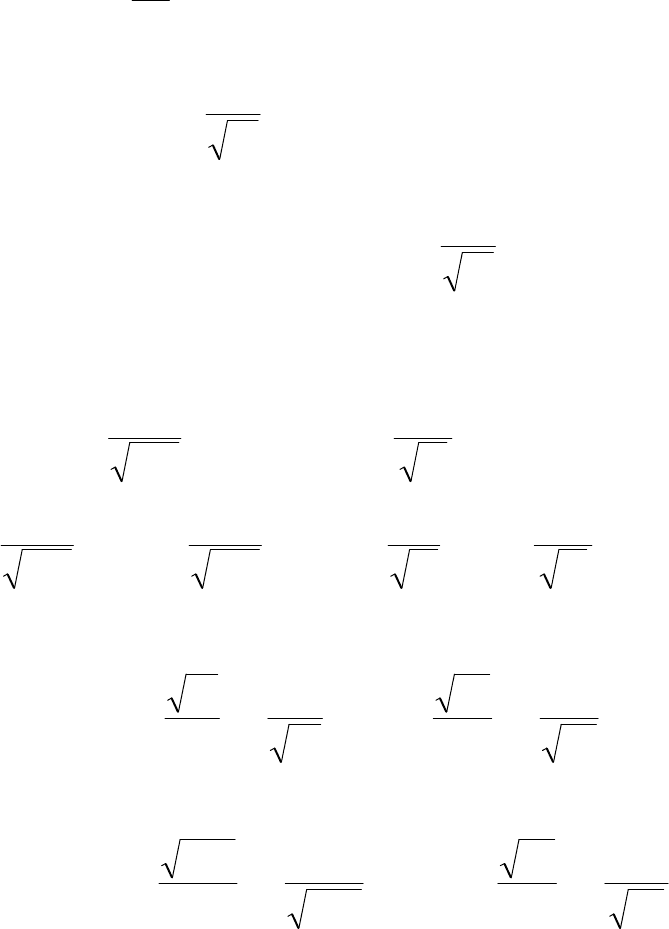
395
Начальные условия
(
)
(
)
(
)
nixRxfxN
iiiiii
,...1,0,
=
−
=
. (5.28)
Используя метод Фурье, решение задачи (5.7) – (5.9) ищем в виде:
(
)
(
)
(
)
nitxXtxN
iiii
,...1,µexp,
~
2
=−=
.
Подставляя эту функцию в (5.25), получим дифференциальное урав-
нение
0
µ
2
=+
′′
i
i
i
X
a
X
, общее решение которого можно записать в
виде
+=
i
i
i
ii
a
AX
ϕ
µx
sin
~
. Следовательно,
( )
( )
ni
a
tAtxN
i
i
i
iii
,...1,
µx
sinµexp
~
,
~
2
=
+−=
ϕ
.
Удовлетворяя условиям сопряжения (5.27), будем иметь
+=
+
+=
+
−
−
−
−
−
−
−
−
−
−
−
−
,
µ
cosλ
~
µ
cosλ
~
,
µ
sin
~
µ
sin
~
1
1
1
1
1
1
1
1
1
1
1
1
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
ii
i
i
i
a
l
a
A
a
l
a
A
a
l
A
a
l
A
ϕϕ
ϕϕ
(5.29)
.
,
2
n
i
K
=
Отсюда
+=
+
2
2
1
2
2
1
1
1
1
1
µ
λ
µ
λ
ϕϕ
a
l
tg
a
a
l
tg
a
,
. . . . . . . . . . . . . . . (5.30)
+=
+
−
−
−
−
−
−
n
n
n
n
n
n
n
n
n
n
a
l
tg
a
a
l
tg
a
ϕϕ
1
1
1
1
1
1
µ
λ
µ
λ
.
На границах
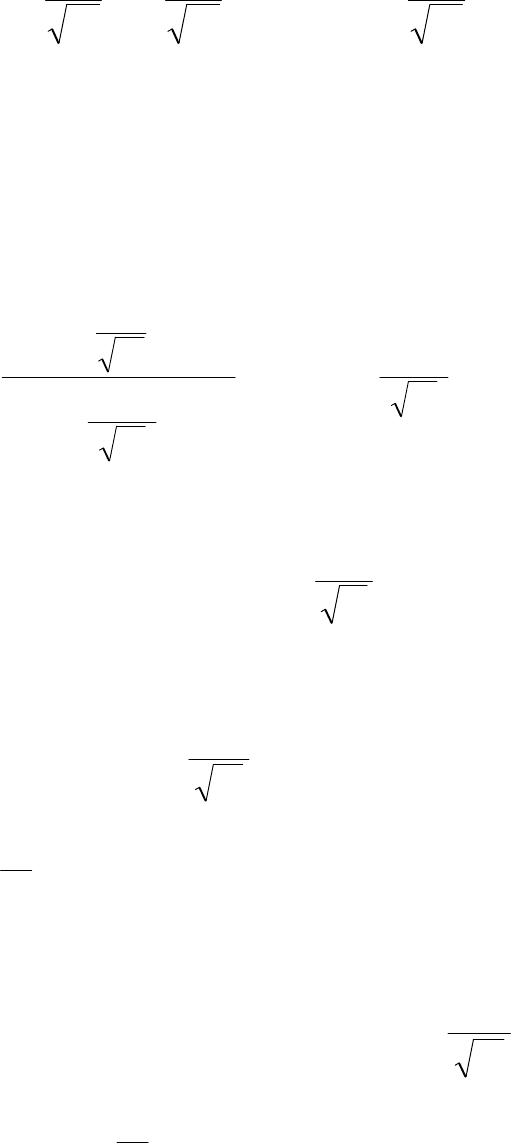
396
0cos
1
=
ϕ
,
0
µ
sincos =
++
+
n
n
n
n
n
n
n
n
a
l
a
l
a
ϕαϕ
µµλ
. (5.31)
Из системы (5.30), (5.31) определяем последовательность соб-
ственных чисел 0
>
k
µ
и значений
k
ϕ
, соответствующих этим чис-
лам. Используя первое равенство (5.27), получим:
niAMA
kkiki
K,3,
~
~
111
==
−−
, где ,1
1
=
k
M
0
µ
sin,
µ
sin
µ
sin
1
1
2
1
1
П
П
≠
+
+
+
=
−
−
=
−
=
rk
r
rk
rk
r
rk
i
r
rk
r
rk
i
r
ik
a
l
a
l
a
l
M
ϕ
ϕ
ϕ
. (5.32)
Таким образом, решение задачи (5.25) - (5.28):
( )
( )
.,2,1,
µ
sinµexp
~
,
1
2
1
∑
∞
=
=
+−=
k
ik
i
ik
kikkii
ni
a
x
tMAtxN K
ϕ
Постоянные
k
A
1
~
определяем, используя ортогональность функций
( )
+=
ik
i
ik
ikiik
a
x
MxX
ϕ
µ
sin
на отрезке
[
]
n
l,0 :
( ) ( )
∑
∫
=
−
≠
=
=
n
i
l
l
iiipiik
i
i
i
i
pk
pkconst
dxxXxX
a
1
1
.
,0
,
λ
Из начальных условий имеем
( ) ( ) ( )
∑
∞
=
+=−=
1
1
µ
sin
~
0,
k
ik
i
ik
ikkiiiiii
a
x
MAxRxfxN
ϕ
.
Умножим обе части на
( )
iip
i
i
xX
a
λ
и, интегрируя на
[
]
ii
ll ,
1−
, получим:
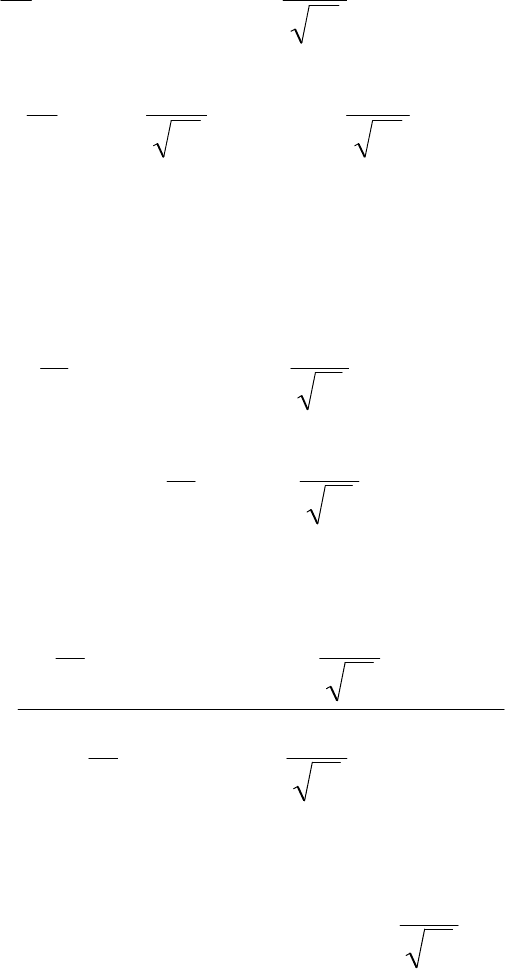
397
( )
∫
−
=
+
i
i
l
l
iip
i
ip
iiip
i
i
dx
a
x
xNM
a
1
µ
sin0,
λ
ϕ
.,...1,
µ
sin
µ
sin
λ
~
1
1
1
∑
∫
∞
=
−
=
+
+=
k
l
l
iip
i
ip
ik
i
ik
i
i
ikipk
i
i
nidx
a
x
a
x
a
MMA
ϕϕ
Суммируя по i от 1 до n и используя ортогональность
ik
X , будем
иметь:
( )
=
+
∑
∫
=
−
iip
i
ip
n
i
l
l
iip
i
i
dx
a
x
xNM
a
i
i
ϕ
µ
sin0,
λ
1
1
.
µ
sin
λ
~
1
22
1
1
∑
∫
=
−
+=
n
i
l
l
iip
i
ip
i
i
ipp
i
i
dx
a
x
a
MA
ϕ
Отсюда:
( )
iip
i
ip
n
i
l
l
ip
i
i
iip
i
ip
n
i
l
l
iip
i
i
p
dx
a
x
M
a
dx
a
x
xNM
a
A
i
i
i
i
+
+
=
∑
∫
∑
∫
=
=
−
−
ϕ
ϕ
µ
sin
λ
µ
sin0,
λ
~
2
1
2
1
1
1
1
. (5.33)
Таким образом, решение задачи (5.19) - (5.23):
( )
( )
+−
∑
++=
∞
=
ik
i
ik
k
k
ikkiiiii
a
x
tMABxAtxT
ϕ
µ
sinµexp
~
,
2
1
1
, (5.34)
в котором коэффициенты
kikii
AMBA
1
~
,,,
определяются по форму-
лам (5.24), (5.32), (5.33). Ряд (5.34) при любом
0
≥
t
сходится абсо-
лютно и равномерно по
],[
1 iii
llx
−
∈
.
Следовательно, температура
i
-го слоя обуви:
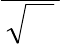
398
(
)
(
)
( )
.
µ
sinµexp
~
,,
2
1
1
+−+++=
=
+
=
∑
∞
=
ik
i
ik
k
k
ikkiiic
ciiii
a
x
tMABxAT
TtxTtx
ϕ
θ
(5.35)
5.4 Решение краевой задачи теплопроводности для верха обуви
и пяточной части (многослойный цилиндр) с граничными условиями
2-4-го рода
В отличие от многослойной пластины внешняя поверхность
таких тел больше чем внутренняя, и это различие будет тем больше,
чем больше будет толщина пакета материалов, формирующих детали
обуви, представляющих собой многослойные полые цилиндры.
Итак, рассмотрим задачу о распределении температуры
−
i
i
θ
го слоя в деталях обуви, представляющих собой цилиндриче-
скую многослойную стенку. Температура окружающей среды под-
держивается постоянной, равной
0
θ
. От стопы на внутреннюю по-
верхность обуви поступает тепловой поток плотности
q
. На внешней
поверхности обуви происходит теплообмен с окружающей средой по
закону Ньютона с коэффициентом теплообмена
.
α
Введем следующие обозначения:
t
− время;
0
),(
θ
θ
−
=
ii
trT
− относительная температура
i
-го слоя;
i
λ
− коэффициент теплопроводности
i
-го слоя;
i
a
− коэффициент
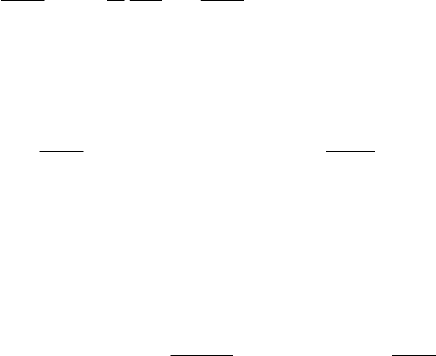
399
температуропроводности
i
-го слоя;
ii
RR ,
1−
− внутренний и внешний
радиусы
i
-го слоя;
.
2
,
1
n
i
K
=
Теперь рассмотрим
−
n
слойный полый цилиндр и краевую за-
дачу
,
1
∂
∂
∂
∂
=
∂
∂
r
T
r
rr
a
t
T
i
i
i
0,
1
>
<
<
−
tRrR
ii
,
.
2
,
1
n
i
K
=
(5.36)
с краевыми условиями
( )
0,
0
1
1
=+
∂
∂
qtR
r
T
λ
;
( ) ( )
0,, =+
∂
∂
tRTtR
r
T
nnn
n
n
αλ
; (5.37)
между слоями предполагается идеальный контакт
(
)
(
)
tRTtRT
iiii
,,
111
−−−
=
;
( ) ( )
tR
r
T
tR
r
T
i
i
ii
i
i
,,
11
1
1 −−
−
−
∂
∂
=
∂
∂
λλ
,
.
,..,
2
n
i
=
(5.38)
начальные условия
.,..,1,),()0,(
1
niRrRrrT
iiii
=
≤
≤
=
−
ϕ
(5.39)
Функция
)(r
i
ϕ
– дважды непрерывно дифференцируема на
ii
RrR
≤
≤
−1
. Решение задачи (5.36) - (5.39) ищем в виде
,,..,1),,()(),( nitrNrQtrT
iii
=
+
=
где
−
)(rQ
i
решения однородной системы
niQr
i
K,1,0)(
=
=
′
′
(5.40)
с краевыми условиями
.,..,2),()(),()(
,0)()(,0)(
1111111
011
niRQRQRQRQ
RQRQqRQ
iiiiiiiiii
nnnnn
=
′
=
′
=
=
+
′
=
+
′
−−−−−−−
λλ
α
λ
λ
(5.41)
Из системы (5.40)
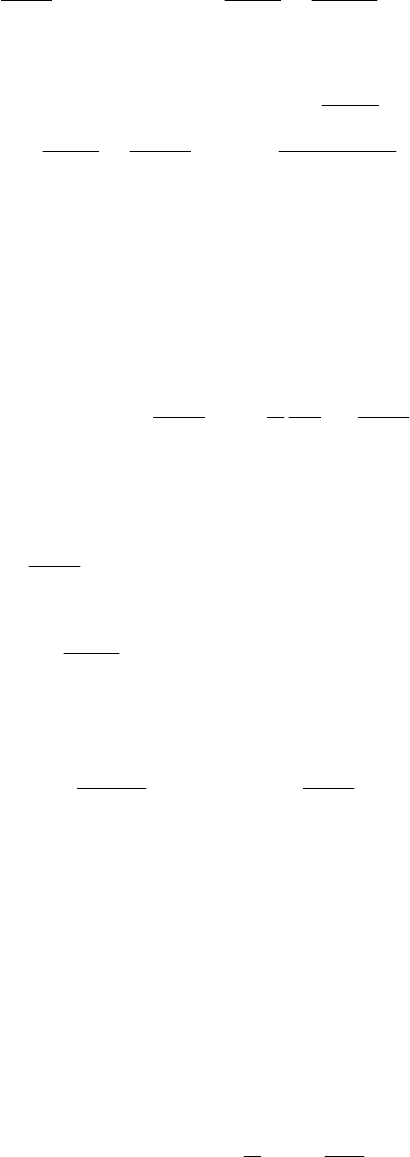
400
.1,..,1,
ln
ln
1
~
,
ln1
~
,
~
,,
~
ln
~
1
1
0
0
0
1
−=
++=
+=−=
≤≤+=
∑
+=
−
−
ni
R
R
R
R
qRB
R
R
qRB
qR
A
RrRBrAQ
n
ik
k
k
k
i
i
n
i
n
n
n
n
i
i
iiiii
λλα
λαλ
(5.42)
Функция
),( trN
i
является решением однородной нестационарной за-
дачи
∂
∂
∂
∂
=
∂
∂
r
N
r
rr
a
t
N
i
i
i
1
(5.43)
с краевыми условиями
( )
( ) ( )
( ) ( )
( ) ( )
nitR
r
N
tR
r
N
tRNtRN
tRNtR
r
N
tR
r
N
i
i
ii
i
i
iiiiii
nnn
n
n
,..,2,,,
,,,
,0,,
,0,
11
1
1
1111
0
1
=
∂
∂
=
∂
∂
=
=+
∂
∂
=
∂
∂
−−
−
−
−−−−
λλ
λλ
αλ
(5.44)
и начальными условиями
nirQrrN
iii
,..,1),()()0,(
=
−
=
ϕ
(5.45)
Решение задачи (5.43) с краевыми условиями (5.44) будем искать в
виде
].,[),()exp(),(
1
2
iiii
RRrrFttrP
−
∈−=
µ
Подставляя это выражение в систему (5.43), получим
0
1
2
2
=+
′
+
′′
iii
F
a
F
r
F
µ
. (5.46)
