Прохоров В.Т. Особенности защиты человека от воздействия низких температур
Подождите немного. Документ загружается.

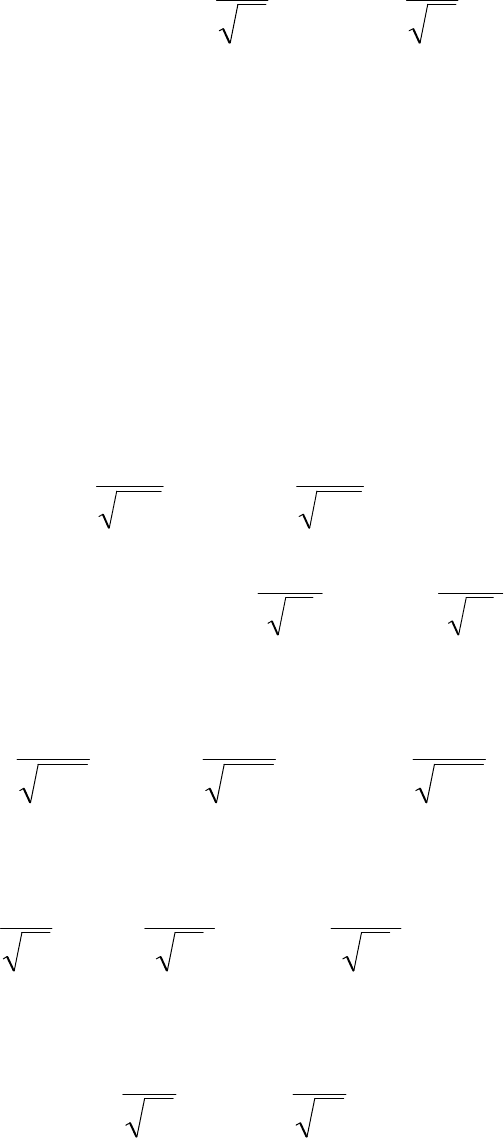
401
Общее решение этого уравнения
,),(
00
+
= r
a
YDr
a
JCtrF
i
i
i
ii
µµ
(5.47)
где
−
)(),( xYxJ
pp
функции Бесселя первого и второго рода индекса
.
p
Решение (5.47) должно удовлетворять условиям
niRFRF
RFRF
RFRF
RF
i
i
i
i
i
i
iiii
ninin
i
,..,2,0)()(
),()(
,0)()(
,0)(
1
1
1
1
111
0
==
′
+
′
=
=+
′
=
′
−−−−
−−−
λλ
αλ
или
,
1
0
1
0
1
1
01
1
1
01
+
=
=
+
−−
−
−
−
−
−
−
i
i
i
i
i
i
i
i
i
i
i
i
a
R
YD
a
R
JC
a
R
YD
a
R
JC
µµ
µµ
(5.48)
=
+
−
−
−
−
−
−
−
−
1
1
11
1
1
11
1
1
i
i
i
i
i
i
i
i
a
R
YD
a
R
JC
a
µµλ
(5.49)
+
=
−−
i
i
i
i
i
i
i
i
a
R
YD
a
R
JC
a
1
1
1
1
µµλ
,
n
i
,..,
2
=
.
0
1
0
11
1
0
11
=
+
a
R
YD
a
R
JC
µµ
. (5.50)
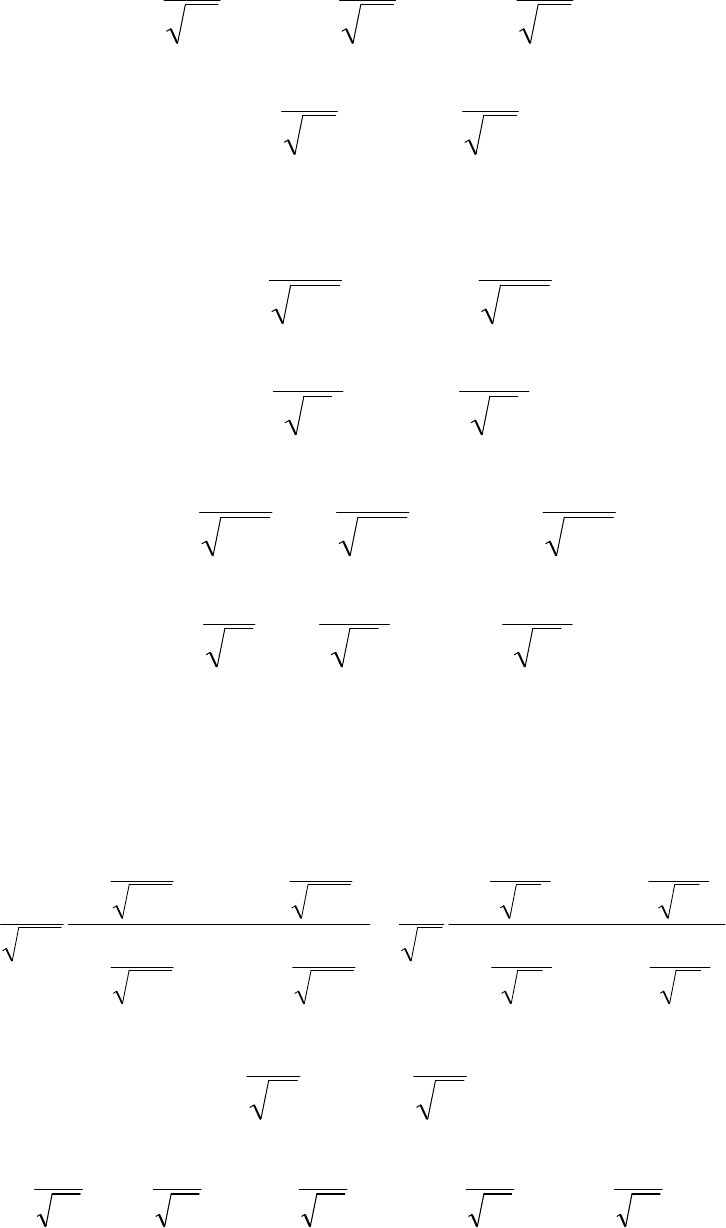
402
.0
00
11
=
+
+
+
+
−
n
n
n
n
n
n
n
n
n
n
n
n
n
n
a
R
YD
a
R
JC
a
R
YD
a
R
JC
a
µµ
α
µµ
µ
λ
(5.51)
Из (5.48) и (5.49)
,
1
0
1
0
1
1
01
1
1
01
+
=
=
+
−−
−
−
−
−
−
−
i
i
i
i
i
i
i
i
i
i
i
i
a
R
YA
a
R
JC
a
R
YA
a
R
JC
µµ
µµ
(5.52)
,
1
1
1
1
1
1
11
1
1
1
1
1
1
+
=
=
+
−−
−
−
−
−
−
−
−
−
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
a
R
YA
a
R
J
a
C
a
R
YA
a
R
J
a
C
µµλ
µµλ
(5.53)
Разделив (5.52) на (5.53), получим
,
1
1
1
0
1
1
1
1
1
1
01
1
1
0
1
1
11
1
1
1
1
1
+
+
=
+
+
−−
−−
−
−
−
−
−
−
−
−
−
−
−
−
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
a
R
YA
a
R
J
a
R
YA
a
R
J
a
a
R
YA
a
R
J
a
R
YA
a
R
J
a
µµ
µµ
λ
µµ
µµ
λ
(5.54)
,0
1
0
11
1
0
1
=
+
a
R
YA
a
R
J
µµ
(5.55)
,0
0011
=
+
+
+
−
n
n
n
n
n
n
n
n
n
n
n
n
a
R
YA
a
R
J
a
R
YA
a
R
J
a
µµ
α
µµ
µ
λ
(5.56)
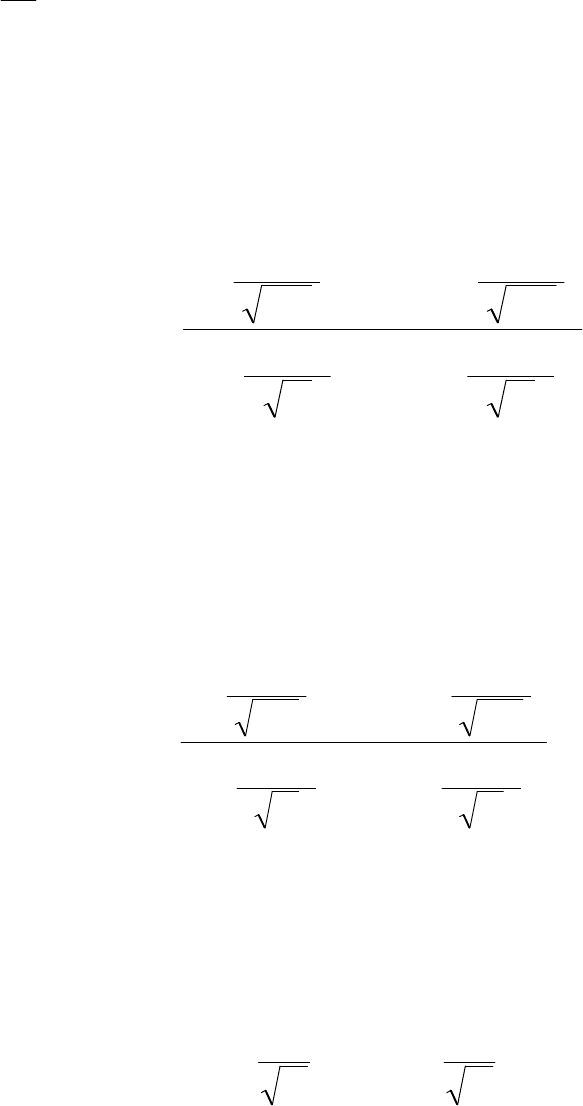
403
где
.
i
i
i
C
D
A =
Из системы (5.54) - (5.56) находим последовательность
собственных чисел
0
>
k
µ
и соответствующие им коэффициенты
.,..,1,..,2,1, nikA
ik
=
=
Далее, используя формулы (5.52), последова-
тельно находим для каждого фиксированного
1
≥
k
∏
=
−−
−
−
−
−
−
+
+
=
m
i
i
ik
ki
i
ik
i
ik
ki
i
ik
m
a
R
YA
a
R
J
a
R
YA
a
R
J
CC
2
1
0,
1
0
1
1
0,1
1
1
0
1
µµ
µµ
. (5.57)
Введем в (5.57) новые обозначения
,..,2,1,,..,1,
,
=
=
=
knmCC
kmm
подчеркивая тем самым зависи-
мость от
k
. Положим также
∏
=
−−
−
−
−
−
−
+
+
=
m
i
i
ik
ki
i
ik
i
ik
ki
i
ik
km
a
R
YA
a
R
J
a
R
YA
a
R
J
M
2
1
0,
1
0
1
1
0,1
1
1
0
,
µµ
µµ
. (5.58)
Тогда ,
,,1, kmkkm
MCC
=
где 1
,1
=
k
M
K
,
2
,
1
,
,..,
1
,
=
=
k
n
m
Таким образом,
).exp(),(
2
0,0,,1,
t
a
r
YA
a
r
JMCtrP
i
k
ki
i
k
kikki
µ
µµ
−
+
=
Чтобы теперь удовлетворить начальным условиям составим функцию
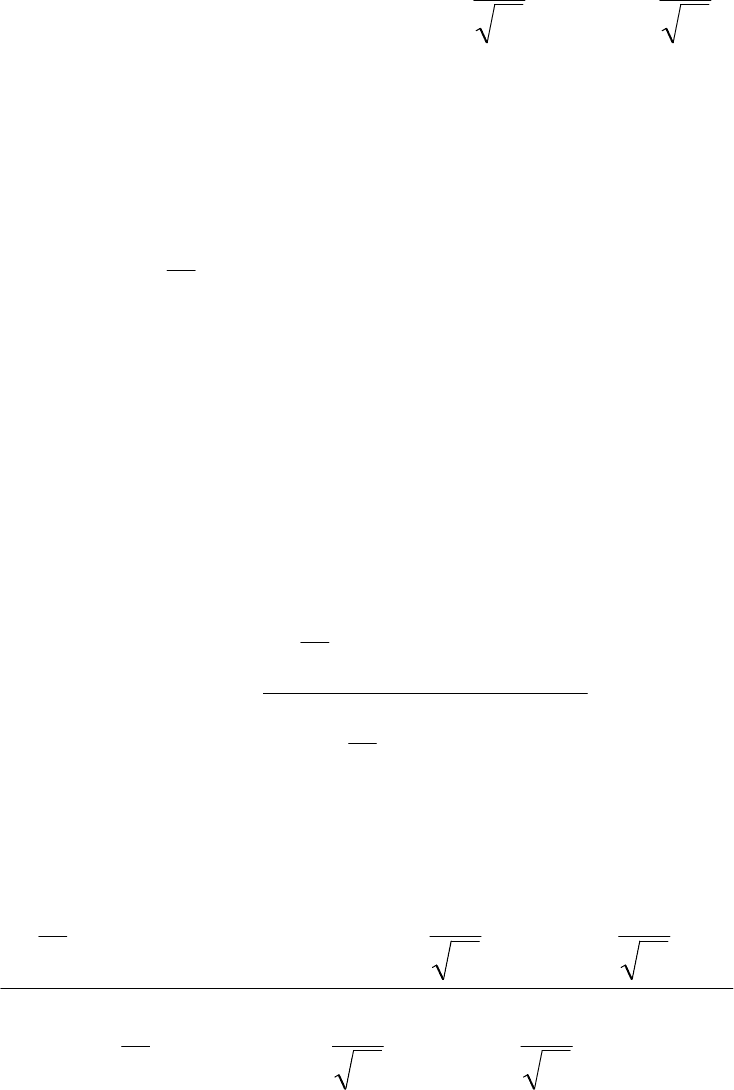
404
).exp(),(),(
2
1
0,0,,1
1
,
t
a
r
YA
a
r
JMCtrPtrN
k
k
i
k
ki
i
k
kik
k
kii
µ
µµ
−
+
==
∑∑
∞
=
∞
=
Неизвестные
k
C
,1
определим из условия ортогональности функций
),(
,
trF
ki
с весом
r
на отрезке
[
]
n
RR ,
0
:
=
≠
=
∫
∑
−
=
.,
;,0
)()(
1
,,
1
pkconst
pk
drrFrrF
a
i
i
R
R
piki
n
i
i
i
λ
Удовлетворяя начальным условиям (5.45),
∑
∞
=
=−=
1
,
).()()()0,(
k
kiiii
rFrQrrN
ϕ
Умножая обе части равенства на
)(
,
rrF
pi
и используя условия орто-
гональности, получим, что
==
∑
∫
∑
∫
=
=
−
−
n
i
R
R
pi
i
i
n
i
R
R
pii
i
i
p
i
i
i
i
drrrF
a
drrrFrN
a
C
1
2
,
1
,
,1
1
1
)(
)()0,(
λ
λ
(5.59)
( )
.
)()(
1
2
0,0
2
,
1
0,0,
1
1
∑
∫
∑
∫
=
=
−
−
+
+
−
=
n
i
R
R
i
p
pi
i
p
pi
i
i
n
i
R
R
i
p
pi
i
p
piii
i
i
i
i
i
i
dr
a
r
YA
a
r
JrM
a
dr
a
r
YA
a
r
JrMrQr
a
µµ
λ
µµ
ϕ
λ
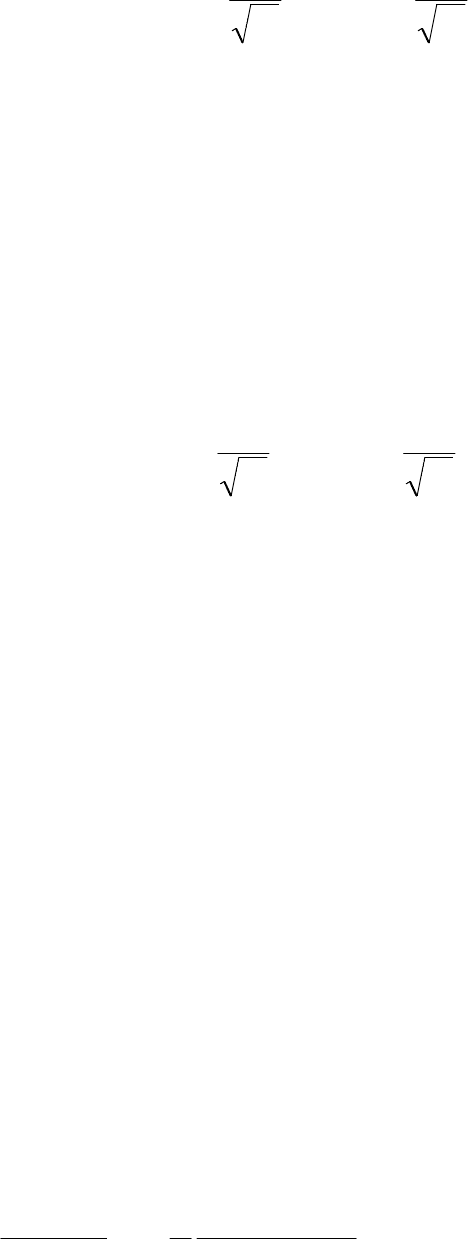
Таким образом,
++=+=
iiiii
BrAtrNrQtrT
~
ln
~
),()(),(
405
),exp(
2
1
0,0,,1
t
a
r
YA
a
r
JMC
k
k
i
k
ki
i
k
kik
µ
µµ
−
+
+
∑
∞
=
(5.60)
где коэффициенты
ikkii
MCBA ,,
~
,
~
1
вычисляются по формулам (5.42),
(5.58), (5.59). Ряд (5.60) сходится равномерно и абсолютно на отрезке
],[
1 ii
RR
−
при любом
0
≥
t
.
Окончательно получаем температуру
i
- го слоя обувного ци-
линдрического пакета
+++=++=+=
iiiiii
BrAtrNrQtrTtr
~
ln
~
),()(),(),(
000
θθθθ
)exp(
2
1
0,0,,1
t
a
r
YA
a
r
JMC
k
k
i
k
ki
i
k
kik
µ
µµ
−
+
+
∑
∞
=
. (5.61)
5.5 Решение краевой задачи теплопроводности для носочной
части обуви (многослойный шаровой сегмент) с граничными усло-
виями 2-4-го рода
В модели ботинка (рис. 5.1) носочная часть представляет мно-
гослойный полый шаровой сегмент. Рассмотрим для такого шарового
сегмента соответствующую краевую задачу.
Пусть
−
),( tr
ii
θ
температура
−
i
го слоя с коэффициентом теп-
лопроводности
,
i
λ
−
c
θ
температура окружающей среды. Обозначим
через
−
−
=
cii
T
θ
θ
относительную температуру
−
i
го слоя
).
,...,
1
(
n
i
=
Прохождение тепла через многослойную шаровую стенку
описывается системой уравнений теплопроводности:
,
)),((
1
),(
2
2
i
iii
i
i
ii
r
trTr
r
a
t
trT
∂
∂
=
∂
∂
,0,
1
>
<
<
−
tRrR
iii
(5.62)
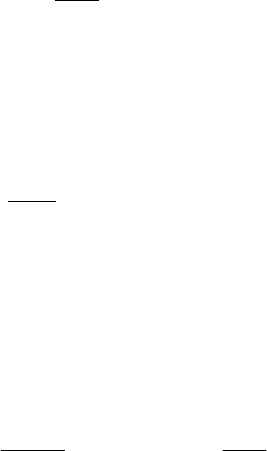
406
где
−
− ii
RR ,
1
внутренний и внешний радиусы
−
i
го слоя,
−
t
время,
−
i
a
коэффициент температуропроводности
−
i
го слоя,
).
,...,
1
(
n
i
=
На внутреннюю поверхность шарового сегмента от стопы по-
ступает тепловой поток плотности
:
q
( )
.0,
0
1
1
1
=+
∂
∂
qtR
r
T
λ
(5.63)
На внешней поверхности тела теплообмен с окружающей средой про-
исходит по закону Ньютона с коэффициентом теплоотдачи
α
:
( ) ( )
.0,, =+
∂
∂
tRTtR
r
T
nnn
n
n
n
αλ
(5.64)
Будем предполагать, что между слоями существует идеальный кон-
такт, который выражается следующими соотношениями:
(
)
(
)
( ) ( )
,,,
,,,
11
1
1
1
111
tR
r
T
tR
r
T
tRTtRT
i
i
i
ii
i
i
i
iiii
−−
−
−
−
−−−
∂
∂
=
∂
∂
=
λλ
(5.65)
.
,...,
2
n
i
=
В начальный момент времени задается температура обуви
(
)
),(0,
iiii
rrT
ϕ
=
n
i
,...,
1
=
(5.66)
Таким образом
,
процесс прохождения тепла через шаровой
сегмент от стопы к внешней поверхности обуви описывается краевой
задачей (5.62) - (5.65) с начальными условиями (5.66).
Решение задачи будем искать в виде
),,()(),(
trNrQtrT
iiiiii
+
=
(5.67)
где
−
)(
ii
rQ
решение однородной системы
( )
,0=
″
ii
Qr
n
i
,...,
1
=
(5.68)
с краевыми условиями:
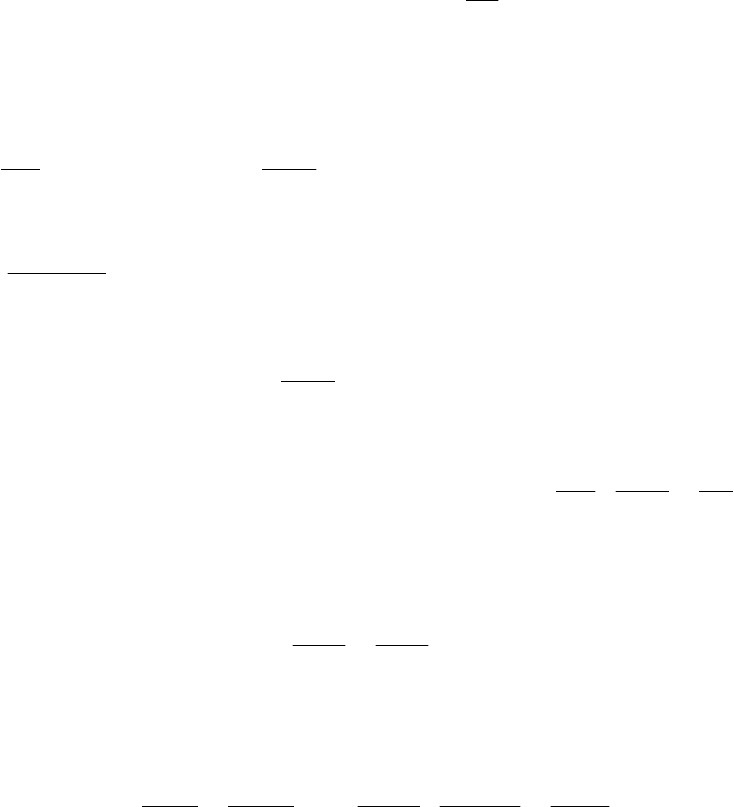
407
0)(
011
=
+
′
qRQ
λ
, (5.69)
0)()( =+
′
nnnnn
RQRQ
αλ
, (5.70)
),()(
111 −−−
=
iiii
RQRQ
(5.71)
niRQRQ
iiiiii
,..,2),()(
1111
=
′
=
′
−−−−
λ
λ
(5.72)
Из системы (5.68) находим, что
,
i
i
ii
r
B
AQ +=
n
i
,...,
1
=
. Теперь оп-
ределим коэффициенты
i
A
и
.
i
B
Из равенства (5.69) находим, что
0
2
0
1
1
=+− q
R
B
λ
или
.
1
2
0
1
λ
qR
B =
Из равенства (5.72) получим, что
.
11
i
ii
i
B
B
λ
λ
−−
=
Откуда
.,..,1,
2
0
ni
qR
B
i
i
==
λ
(5.73)
Подставляя
n
Q
в равенство (5.70) находим
.
11
2
0
−=
nnn
n
RR
R
qA
λα
Из формулы (5.71) получаем рекуррентное соотношение
.,..,2,
1
1
1
1
ni
R
B
R
B
AA
i
i
i
i
ii
=−+=
−
−
−
−
Отсюда следует, что
.
11111
1
1
2
2
0
−+−=
∑
−
=
−+−−
in
k
knknknnn
n
i
RR
R
qRA
λλλ
α
(5.74)
Таким образом, решением задачи (5.68) - (5.72) является функция

408
,,)(
1 iii
i
i
iii
RrR
r
B
ArQ ≤≤+=
−
в которой коэффициенты
i
A
и
i
B
вычисляются по формулам (5.73), (5.74).
Функции
),( trN
ii
в формуле (5.67) будем искать как решение
краевой задачи
.,..,1,
)(
1
2
2
ni
r
rN
r
a
t
N
i
ii
i
i
i
=
∂
∂
=
∂
∂
(5.75)
( ) ( ) ( )
( ) ( )
( ) ( )
.,,
,,,
,0,,,0,
11
1
1
1
111
0
1
1
tR
r
N
tR
r
N
tRNtRN
tRNtR
r
N
tR
r
N
i
i
i
ii
i
i
i
iiii
nnn
n
n
n
−−
−
−
−
−−−
∂
∂
=
∂
∂
=
=+
∂
∂
=
∂
∂
λλ
αλ
(5.76)
В свою очередь, воспользовавшись методом Фурье, найдем
функцию
(
)
),exp()(,
2
trFtrP
iiii
µ
−=
удовлетворяющую задаче
(5.75), (5.76). Подставляя
i
P
в (5.75) и (5.76), получим краевую задачу
относительно функции
:)(
ii
rF
( )
.,..,1,0)()(
2
nirFrFr
r
a
iiiii
i
i
==+
″
µ
(5.77)
(
)
.,..,2),()(),()(
,0)(,0)(
1111111
01
niRFRFRFRF
RFRFRF
iiiiiiiiii
nnnnn
=
′
=
′
=
=
+
′
=
′
−−−−−−−
λλ
α
λ
(5.78)
Общее решение уравнения (5.77) имеет вид
.sin
1
sin
1
cos
1
sin
1
)(
22
+=
++=
=+=
i
i
i
i
ii
i
i
i
ii
i
i
i
i
i
i
i
iii
a
r
r
w
a
r
r
DC
a
r
r
D
a
r
r
CrF
ϕ
µ
ϕ
µ
µ
µ
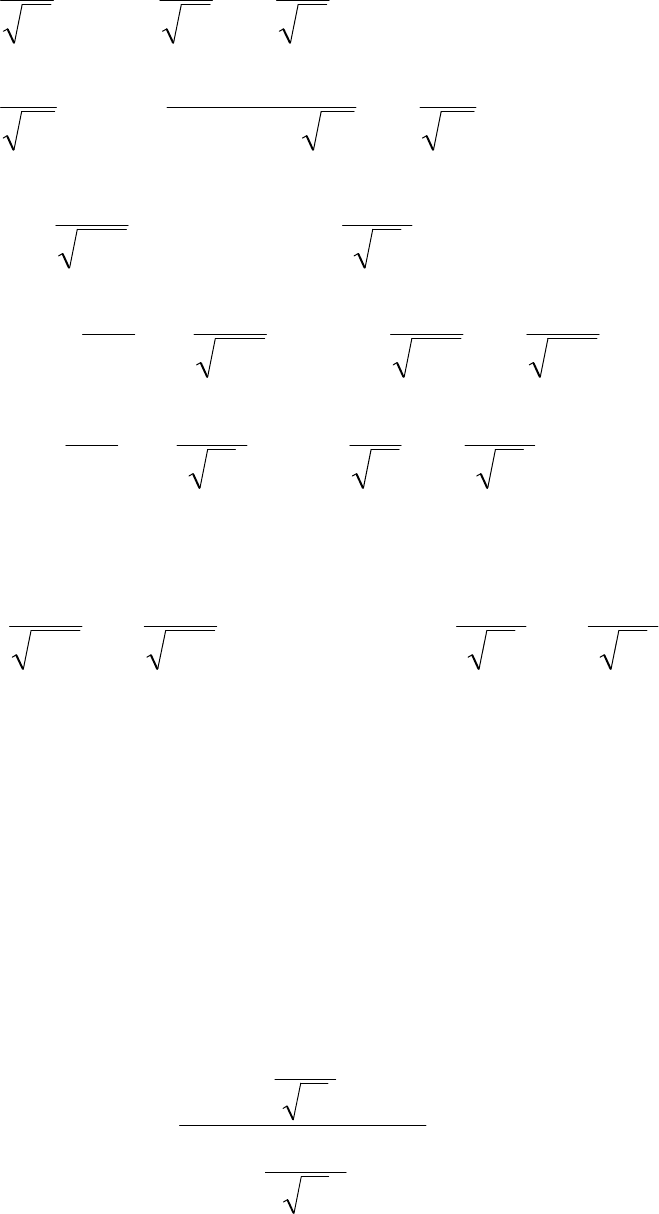
409
Удовлетворяя краевым условиям, получим систему уравнений
( )
,cossin
,cossin
1
1
0
1
0
1
1
0
+
−
=
+
+=
+
n
n
n
nnn
nn
n
n
n
a
R
aR
R
a
R
a
R
a
R
a
R
ϕ
µ
αλ
λµ
ϕ
µ
ϕ
µµ
ϕ
µ
(5.79)
,cossin
1
cossin
1
,sinsin
11
1
1
1
1
1
1
1
1
1
11
1
1
1
1
1
++
+−=
++
+−
+=
+
−−
−
−
−
−
−
−
−
−
−
−−
−
−
−
−
−
i
i
i
i
i
i
i
i
ii
i
i
i
i
i
i
i
i
ii
i
i
i
ii
i
i
i
a
R
aa
R
R
w
a
R
aa
R
R
w
a
R
w
a
R
w
ϕ
µ
µ
ϕ
µ
λ
ϕ
µ
µ
ϕ
µ
λ
ϕ
µ
ϕ
µ
(5.80)
.
,..,
2
n
i
=
Исключая
i
w
из уравнений (5.80) получим
,11
11
1
1
1
1
1
1
−
+==
−
+
−−
−
−
−
−
−
− i
i
i
i
i
ii
i
i
i
i
i
a
R
ctg
a
R
a
R
ctg
a
R
ϕ
µµ
λϕ
µµ
λ
.
,..,
2
n
i
=
Добавляя к этому два уравнения (5.79), будем иметь систе-
му
−
+
1
n
го уравнений с
−
+
1
n
м неизвестным:
.,..,,
1 n
ϕ
ϕ
µ
Решая
ее, находим собственные числа
0
>
k
µ
и соответствующие им значе-
ния
..2,1,,..,1,
=
=
kni
ik
ϕ
Из первого уравнения системы (5.80) для
каждого
,...
2
,
1
=
k
можно получить соотношение
,
1kikik
wMw
=
n
i
,..,
1
=
, где
,1
1
=
k
M
.,..,2,
sin
sin
2
1
1
1
ni
a
R
a
R
M
i
l
lk
l
lk
i
l
lk
l
lk
ik
=
+
+
=
∏
∏
=
−
−
=
ϕ
µ
ϕ
µ
(5.81)
410
С учетом полученных соотношений общее решение краевой задачи
(5.75), (5.76) запишем в виде
.sin)exp(
1
),(
2
1
1
+−=
∑
∞
=
ik
i
ik
k
k
ikk
i
ii
a
r
tMw
r
trN
ϕ
µ
µ
Остается вычислить коэффициенты
.
1k
w
Для этого воспользуемся на-
чальными условиями:
∑
∞
=
+=−=
1
1
.sin
1
)()()0,(
k
ik
i
ik
ikk
i
iiiiii
a
r
Mw
r
rQrrN
ϕ
µ
ϕ
(5.82)
Воспользуемся ортогональностью функций
+
ik
i
ik
ik
a
r
M
ϕ
µ
sin
на
отрезке
:],[
0 n
RR
=≠
≠
=
=
∫
+
+
∑
−
=
.,0
,,0
sinsin
1
1
pkприconst
pkпри
dr
a
r
a
r
MM
a
i
R
R
ip
i
ip
ik
i
ik
ipik
n
i
i
i
i
i
ϕ
µ
ϕ
µλ
Умножим обе части равенства (5.82) на
.sin
+
ip
i
ip
ipi
i
i
a
r
Mr
a
ϕ
µ
λ
За-
тем, суммируя по
i
и интегрируя по
],,[
0 n
RR
получим
( )
.sin
sin)()(
1
22
1
1
1
1
∑
∫
∑
∫
=
=
−
−
+=
=
+−
n
i
R
R
iip
i
ip
ipp
i
i
n
i
R
R
iip
i
ip
iipiiii
i
i
i
i
i
i
dr
a
r
Mw
a
dr
a
r
rMrQr
a
ϕ
µ
λ
ϕ
µ
ϕ
λ
Отсюда
