Salby M.L. Fundamentals of Atmospheric Physics

Подождите немного. Документ загружается.

470

14 Atmospheric Waves

where a is the damping rate of temperature perturbations (units of inverse

time), or

(D )3qt'N2w,

+ a ~ + 70 = 0. (14.78.2)

Using (14.78) to eliminate w' in the linearized form of the vorticity equation

(12.47),

[d(sr + f)] ' _

fo 10

d t p -~z (-tim'),

(14.79)

where the left-hand side accounts for shear in the mean flow K = K(y, z),

yields the perturbation vorticity equation

D V21/t ' q- -- O~

D t p ~z ~ N-2 P ~z at- p -~z N-2 P -~z .at- [~e -~x - O,

(14.80)

which is a generalization of (14.75).

Within the framework of the WKB approximation, considering solutions

of the form

exp[(z/2H) + i(kx + ly + mz -

~rt)] transforms (14.80) into the

dispersion relation

[1 + i (=)] m 2 --m 2, (14.81.1)

where

(N_0~) [

/~e

ikhl 2 ]

m 2 -- -~ _ Cx

4H 2 (14.81.2)

satisfies the dispersion relation in the absence of damping (14.77). Solving for

the vertical wavenumber gives

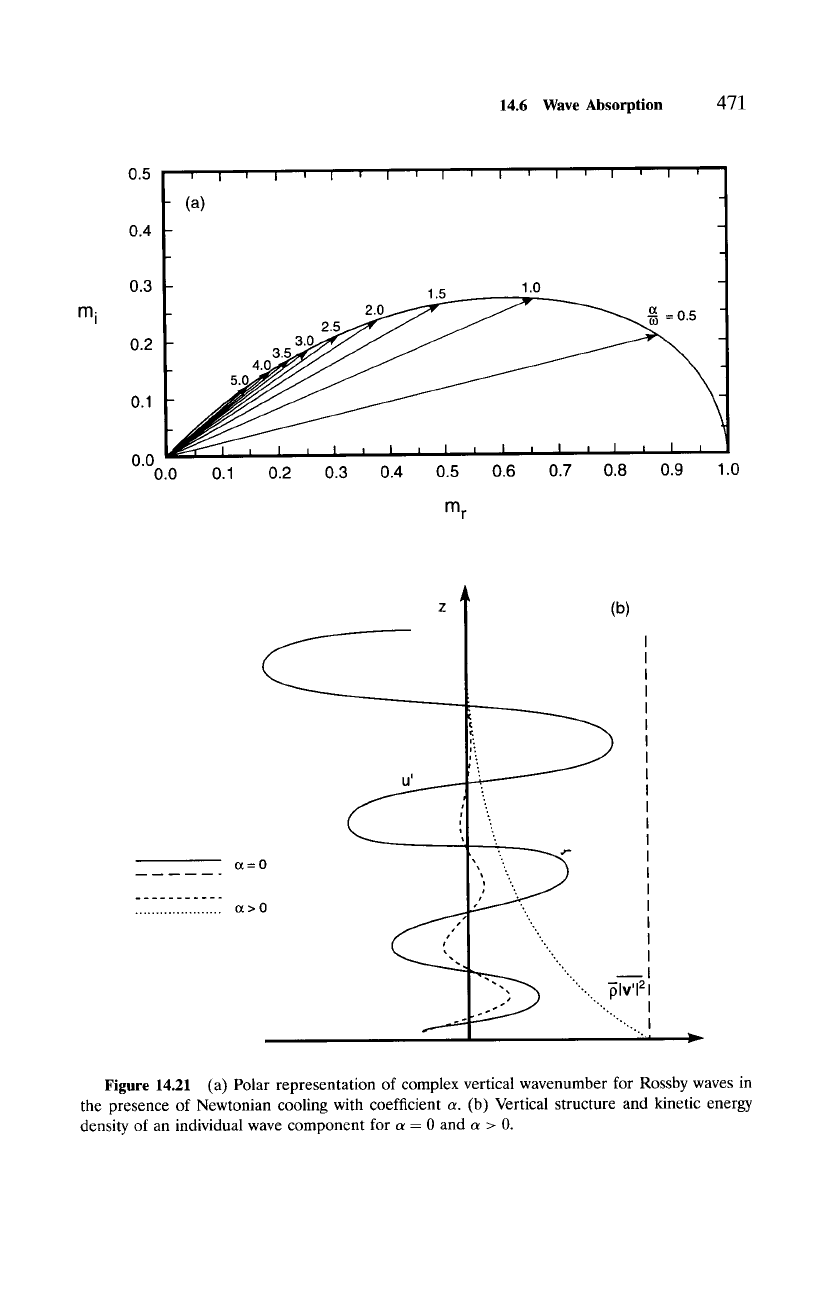
ei(~)

m = m r + im i =

mo,

(14.82.1)

(Fig. 14.21a), where (since oJ < 0)

4~ = tan -1 ~-~ 9 (14.82.2)

An individual wave component has vertical structure

e( l +im)z

e ( ~ -mi)z "

eimr z.

Because m0 > 0 for downward phase propagation, (14.82) implies

m i > O.

Hence, thermal damping introduces an imaginary component to m that off-

sets the vertical amplification of wave activity (Fig. 14.21b). Representing the

ratio of timescales for wave oscillation and damping,

m i

increases with in-

creasing

(o~/w)mo.

Wave amplitude then grows with height more slowly than

under adiabatic conditions, which corresponds to the kinetic energy density

14.6 Wave Absorption

471

m i

0.5

(a)

0.4

0.3

0.2

0.1

0.0

I i I i I ~ I i I i I l I i I i I J

1.5 1.0

2o o o5 1

3.0~

-t

- 3.5 "

_ ~

0.1 0.2 0.3 0.4 05 0.6 0.7 0.8 0.9 1.0

(b)

~=0

..................... 0~>0

"~lv'l 2

"'"".. ,~

Figure 14.21 (a) Polar representation of complex vertical wavenumber for Rossby waves in

the presence of Newtonian cooling with coefficient a. (b) Vertical structure and kinetic energy

density of an individual wave component for a = 0 and a > 0.

472 14

Atmospheric Waves

,[2) decreasing upward as progressively more wave activity is ab-

(e.g.,-~[v

sorbed. For

(a/w)mo

sufficiently large, amplitude itself decreases with height,

so components with small intrinsic frequency or short vertical wavelength de-

cay vertically above their forcing.

In practice, thermal dissipation is introduced whenever the circulation is

driven out of radiative equilibrium. Wave motions do this naturally by advect-

ing air from one radiative environment to another. In the stratosphere, the

polar-night vortex is displaced out of radiative equilibrium by planetary waves,

which drive air across latitude circles (refer to Fig. 1.10). Longwave cooling to

space then acts on individual air parcels in proportion to their departure from

local radiative equilibrium, which destroys anomalous temperature and the

accompanying motion. Air displaced into polar darkness, where the radiative-

equilibrium temperature is very low, finds itself anomalously warm, so it cools

(Fig. 8.27). Conversely, the vortex in the summer stratosphere remains rela-

tively undisturbed and therefore close to radiative equilibrium.

Because it is proportional to the vertical derivative of q~', Newtonian cool-

ing leads to stronger damping of short vertical wavelengths than long vertical

wavelengths. For vertical wavelengths comparable to H, the cool-to-space ap-

proximation breaks down. As shown in Fig. 8.29, LW exchange between neigh-

boring layers then makes a itself strongly scale dependent, being much faster

for short vertical wavelengths than long vertical wavelengths.

Absorption can change along a ray because a varies spatially. According

to Fig. 8.29, the timescale for thermal damping decreases from several weeks

in the troposphere to only a couple of days in the upper stratosphere. Of

greater significance,

(a/~o)mo --+ ~

if the intrinsic frequency is Doppler-

shifted to zero. Near a critical line, oscillations become stationary relative to

the medium, allowing wave activity to be fully absorbed.

14.7 Nonlinear Considerations

Under inviscid adiabatic conditions, the equations governing wave propaga-

tion become singular at a critical line. Dissipation removes the singularity by

absorbing wave activity as the wavelength collapses and cg approaches zero.

Strong gradients near the critical line then magnify thermal damping and dif-

fusion, which, by smoothing out those gradients, act to destroy organized wave

motion. These conclusions follow solely from considerations of the first-order

equations, in which only simple forms of dissipation are represented. More

generally, singular behavior near a critical line invalidates treating the per-

turbation equations in isolation. In the limit of small dissipation, wave stress

exerted on the mean flow (14.5) becomes concentrated at the critical line

and unbounded (Dickinson, 1970). Even with plausible dissipation, the con-

vergence of momentum flux implies large accelerations locally, so ~ cannot be

14.7 Nonlinear Considerations

473

regarded as steady. Further, nonlinear interaction between components of the

wave spectrum can then also become large.

Recall that the governing equations can be linearized as long as second-

order terms such as v'. Vv' are much smaller than those first order in wave

amplitude. Since, for an individual wave component, the material derivative is

d D

= -+- Vf 9 V

dt Dt

: -ito + iv' 9 k

--ik[(cx--~)-v'- . -kk] ,

(14.83)

ignoring second-order behavior is tantamount to requiring the intrinsic trace

speed ICx - ul to be large compared to the eddy velocity Iv'l induced by the

wave. Near a critical line, this requirement breaks down because

ICx--ul

--+ 0. Instead of undergoing a small oscillation during the limited time for

a wavelength to propagate by, an individual parcel then experiences finite

displacements, which can lead to a permanent rearrangement of air. 6

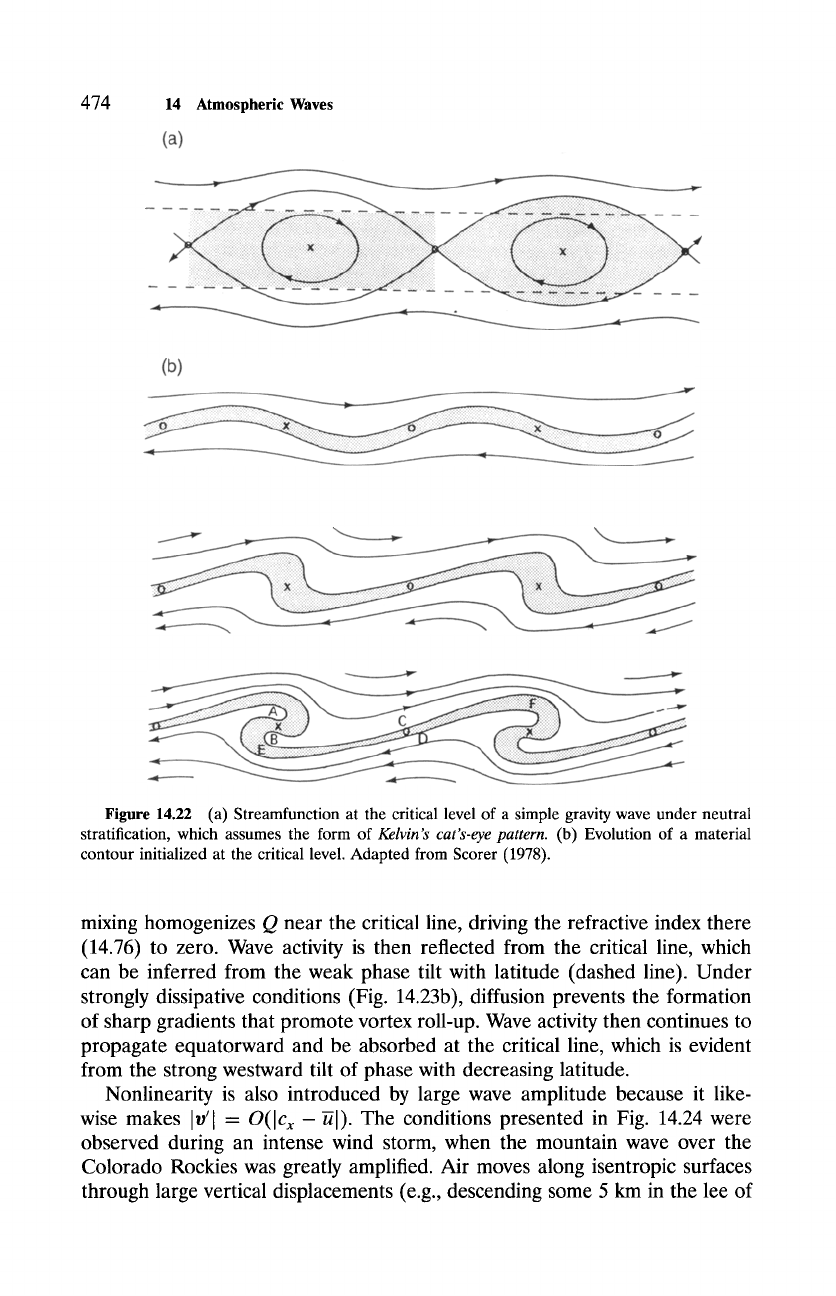
Attention was first drawn to this issue by Kelvin (1880), who noted the pe-

culiar behavior in Fig. 14.22a for the critical level of a gravity wave under

incompressible conditions and neutral stratification. For N 2 = 0, (14.40) im-

plies a total streamfunction relative to the medium that is symmetric about

z - Zc

and contains closed streamlines within some neighborhood of the crit-

ical level. 7 Known as

Kelvin's cat's-eye pattern,

this distribution of qJ describes

a series of vortices that overturn and eventually wind up air inside the criti-

cal region (Fig. 14.22b). Gradients supporting organized wave motion are then

sheared down to small scales, where diffusion can destroy them efficiently, cul-

minating in the absorption of wave activity arriving at the critical level. In the

limit of weak dissipation, another scenario is possible. The vorticity u z is then

a conserved property (Problem 14.25). Therefore, mixing will homogenize the

distribution of vorticity and drive Kz~ to 0, in the same fashion that convec-

tive mixing homogenizes the distribution of potential temperature and drives

30/3z

to zero (Sec. 7.6). Once this condition is achieved, m 2 - 0 in a neigh-

borhood of zc (14.40.2), so wave activity is subsequently reflected from the

critical level.

Rossby waves produce analogous behavior through horizontal advection.

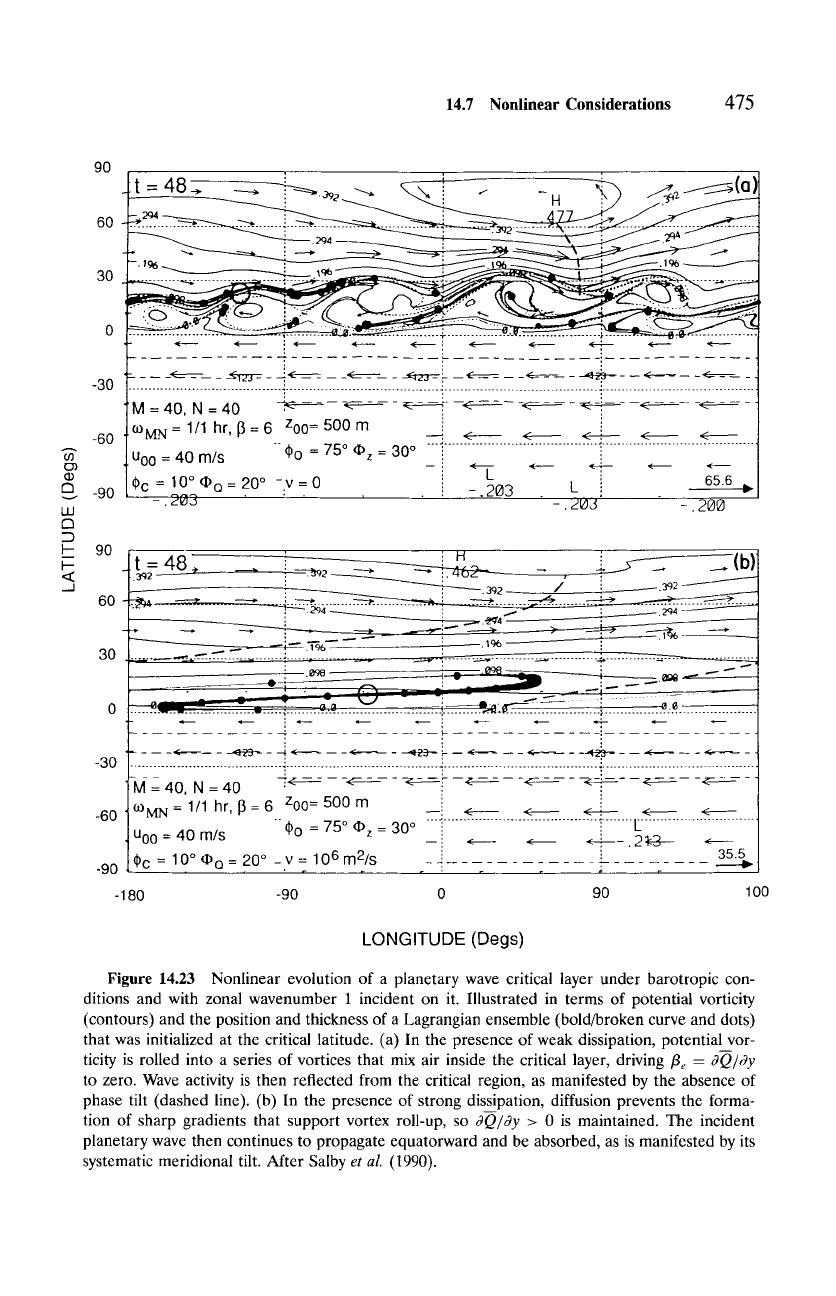
Figure 14.23 shows planetary wave activity incident on a critical line at low

latitude. Under weakly dissipative conditions (Fig. 14.23a), nonlinear advec-

tion near the critical line overturns material lines, which are delineated by

contours of potential vorticity Q. Air inside the critical region is rolled up in a

series of vortices that destroy organized wave motion on large scales by shear-

ing it down to small scales, where diffusion is effective. Efficient horizontal

6Dissipation keeps displacements bounded by introducing an imaginary component to c x -

(Problem 14.53).

7Rossby waves behave similarly, but with/3 e in place of-Kzz-

474

Atmospheric Waves

(a)

(b)

.- ~..~../~.'~"~'"

Figure 14.22 (a) Streamfunction at the critical level of a simple gravity wave under neutral

stratification, which assumes the form of

Kelvin's cat's-eye pattern.

(b) Evolution of a material

contour initialized at the critical level. Adapted from Scorer (1978).

mixing homogenizes Q near the critical line, driving the refractive index there

(14.76) to zero. Wave activity is then reflected from the critical line, which

can be inferred from the weak phase tilt with latitude (dashed line). Under

strongly dissipative conditions (Fig. 14.23b), diffusion prevents the formation

of sharp gradients that promote vortex roll-up. Wave activity then continues to

propagate equatorward and be absorbed at the critical line, which is evident

from the strong westward tilt of phase with decreasing latitude.

Nonlinearity is also introduced by large wave amplitude because it like-

wise makes

Iv'l =

O(Icx-

~1).

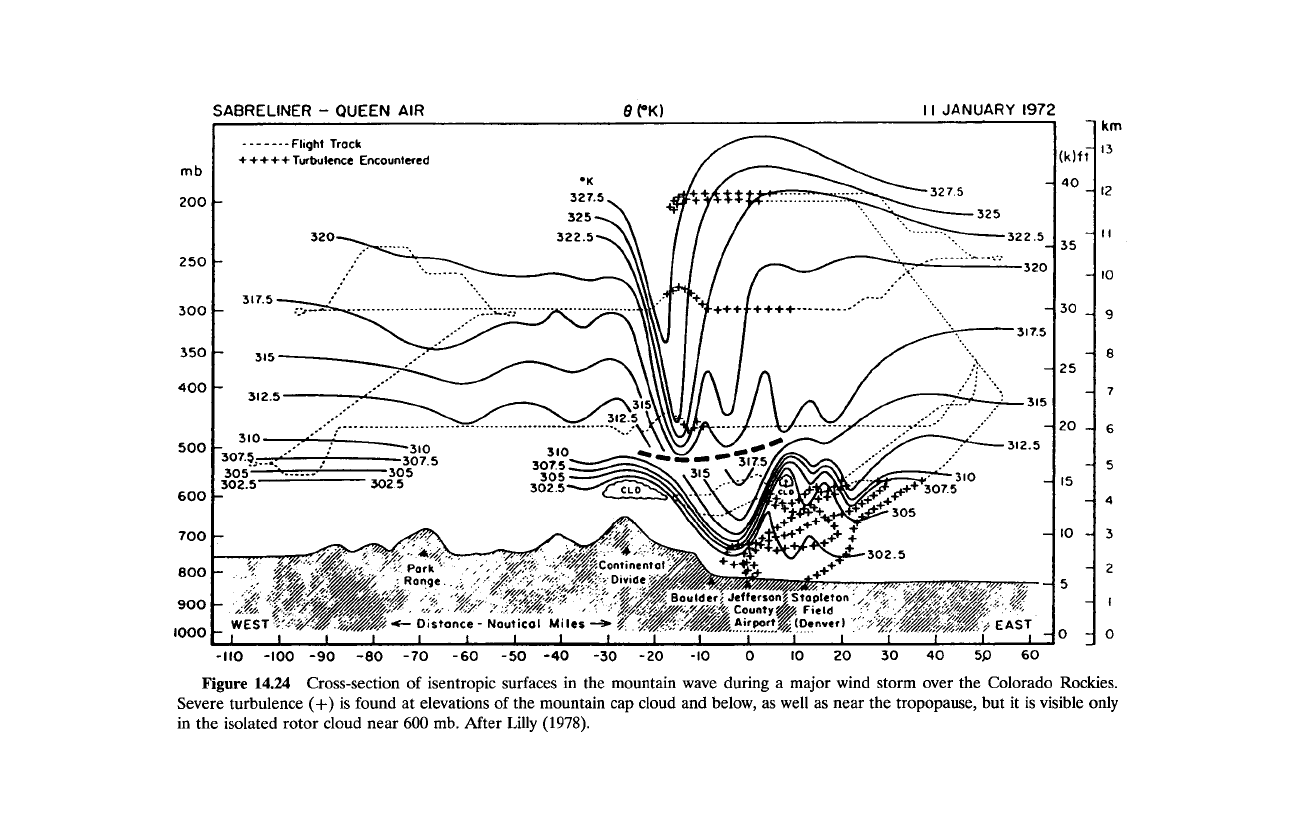
The conditions presented in Fig. 14.24 were

observed during an intense wind storm, when the mountain wave over the

Colorado Rockies was greatly amplified. Air moves along isentropic surfaces

through large vertical displacements (e.g., descending some 5 km in the lee of

14.7 Nonlinear Considerations

475

-60

~.~ -90

F--

...J

_ t = 48_.

----* ~=~ '~

~ " - H

~b ....~,,~~(a)

60 .... ................... ~ ........ :~2-~ ...... -,, ...... ~ .... :~

-----~-L_----.-------2~_

196~

................

~-- ~ !~-- ~-. ~___, < ~ ~ ~ ~

. ,

-30 ....................................... " ............................................................................... " .......................................

M = 4 0, N = 40

,-?<- .... <-

- -- - ~ - --- -<-=-=- -~-=-= - -<--!-=-,'-- -<---=-=--

-,~=-=-=

~tv~ 111hr,~=6 Zoo= 500m i

...., ....................................... -I .......................................

Uoo = 40 m/s " 0o = 75~ Oz = 30~ ~ .--- .,----

% = 10 ~ OQ = 20 ~ -v = 0 - ~ <---- i 65.6

- 203 , : -.203 L i

9 -. 2La~ -. 200

: '. H '. b

t=48 ._. ~ ( )

; ~--~-~ . ~--~~ ~i ~ _ ? ._. __.

~ ::~

---- ,-b--~.~ ~

L------. ~2~

L ..... ..~.~.~_..'E._.,,--. ...... ,: ..... :,. .... - ~--,~ -.~,,-i .~ ..................

: 998_ ~ ~ .090 __ : ..-.-.'~'~ ~

_2'

.................................. }. ........................................

- ~ ~.~ ,, ~ 4.-..- .,.-- ~ ~ ~ 4-..-

' I- :

.... ~,--.~--m _ ~ - --4 '(,------- m - '~,----'---- - --~-2-3-- }-- -- ~ -- -~ - --~2"3 "~ ~ -

-30 ....................................... " ............................................................................... " .......................................

M = 40, N = 40 ~:

.... ~----=-----<-=-=r-~--==--~=-=-----~--~-=-=-- -~--~-- -

-60 o~MN=l/lhr,~l=6 ZOO= 500m --,, < < < ! E <

..... ., ..............................................................................

Uoo=40m/s r =75~176 - < < < -.2~3

(

-90 r 10 ~ 20~ v=10 6m2/s 35.5

-180 -90 0 90 100

LONGITUDE (Degs)

Figure 14.23 Nonlinear evolution of a planetary wave critical layer under barotropic con-

ditions and with zonal wavenumber 1 incident on it. Illustrated in terms of potential vorticity

(contours) and the position and thickness of a Lagrangian ensemble (bold/broken curve and dots)

that was initialized at the critical latitude. (a) In the presence of weak dissipation, potential vor-

ticity is rolled into a series of vortices that mix air inside the critical layer, driving/3 e -

~O/Sy

to zero. Wave activity is then reflected from the critical region, as manifested by the absence of

phase tilt (dashed line). (b) In the presence of strong dissipation, diffusion prevents the forma-

tion of sharp gradients that support vortex roll-up, so

8Q/~y

> 0 is maintained. The incident

planetary wave then continues to propagate equatorward and be absorbed, as is manifested by its

systematic meridional tilt. After Salby

et al. (1990).

200

250

300

350

400

500

600

700

800

900

1000

SABRELINER

OUEEN AIR

CK1

JANUARY

1972

- -

Fliqhl

Track

+++++Turbulence Encountered

Figure

14.24

Cross-section

isentropic surfaces

the mountain wave during a major wind storm over the Colorado Rockies.

Severe turbulence

(+)

found at elevations

the mountain cap cloud and below, as well as near the tropopause, but it is visible

only

in the isolated rotor cloud near

600

rnb.

After Lilly

(1978).

14.7 Nonlinear Considerations 477

the continental divide). The steep slope of isentropic surfaces reduces

dO/dz

and static stability locally. In addition, the large amplitude exaggerates ver-

tical shear. Both effects tend to destabilize the organized motion through

mechanisms discussed in Sec. 13.3. Richardson numbers less than 1 then pro-

duce intense turbulence that damps the wave by cascading energy to small

scales, where it is dissipated efficiently. Advected downstream, that turbu-

lence can be violent and is visible only in the isolated rotor cloud at 600 mb

(Sec. 9.3). During the event shown, a Boeing 707 on approach to Denver air-

port sustained loads of 3

g's.

Similar conditions were encountered during the

1950s in the Sierra Wave Project, when the jet stream was observed by in-

strumented sailplanes. The following excerpt from a chronicle of the project

(Lincoln, 1972) describes an episode familiar to aviators:

Editor's Note: On the day described, Larry Edgar was flying a Pratt-Read, one

of the strongest sailplanes ever built, and he had the ultimate experience of flying

turbulence in the rotor. This story has probably saved the lives of a number of

aviators who have learned the indicated lesson and treat rotor clouds with respect.

"Lloyd Licher and I examined the wreckage and compared notes with others.

The nose pulled off just at the seats, by what seemed to be a tension failure of the

steel tubing. Considering Larry's weight and the instrumentation, this should have

required just in excess of 16 g's .... The wreckage showed the left wing to have

broken at altitude. It broke downward near the root. The tail boom was broken

cleanly from the fuselage pod, at altitude, and appears to have come off upward.

The various control cables going from nose to tail were pulled apart completely--in

a bunch. The force needed to do this should be far over 10, 000 pounds."

JOACHIM P. KUETFNER

(The pilot survived.)

Large amplitude results naturally from vertical propagation. Upon reaching

sufficient height, a gravity wave will have achieved a perturbation potential

temperature 0' large enough to drive the vertical gradient of total potential

temperature to zero locally

30 dO dO'

= --

-t- ~ = 0. (14.84)

dz dz dz

Isentropic surfaces are then vertical, which corresponds to zero static stability.

The gravity wave may then

break

by overturning the stratification, analogous

to a surface water wave incident on a shoreline. Air of low 0 is folded over

air of higher 0, as shown in Fig. 14.25 for a gravity wave that has reached the

mesosphere, so stable stratification is transformed into unstable stratification.

Violating the

criterion for turbulence, the ensuing stratification culminates

in vigorous mixing, with wave momentum being deposited at the site of ab-

sorption. Momentum deposited by gravity waves is thought to be responsible

for driving the zonal-mean circulation of the mesosphere out of radiative

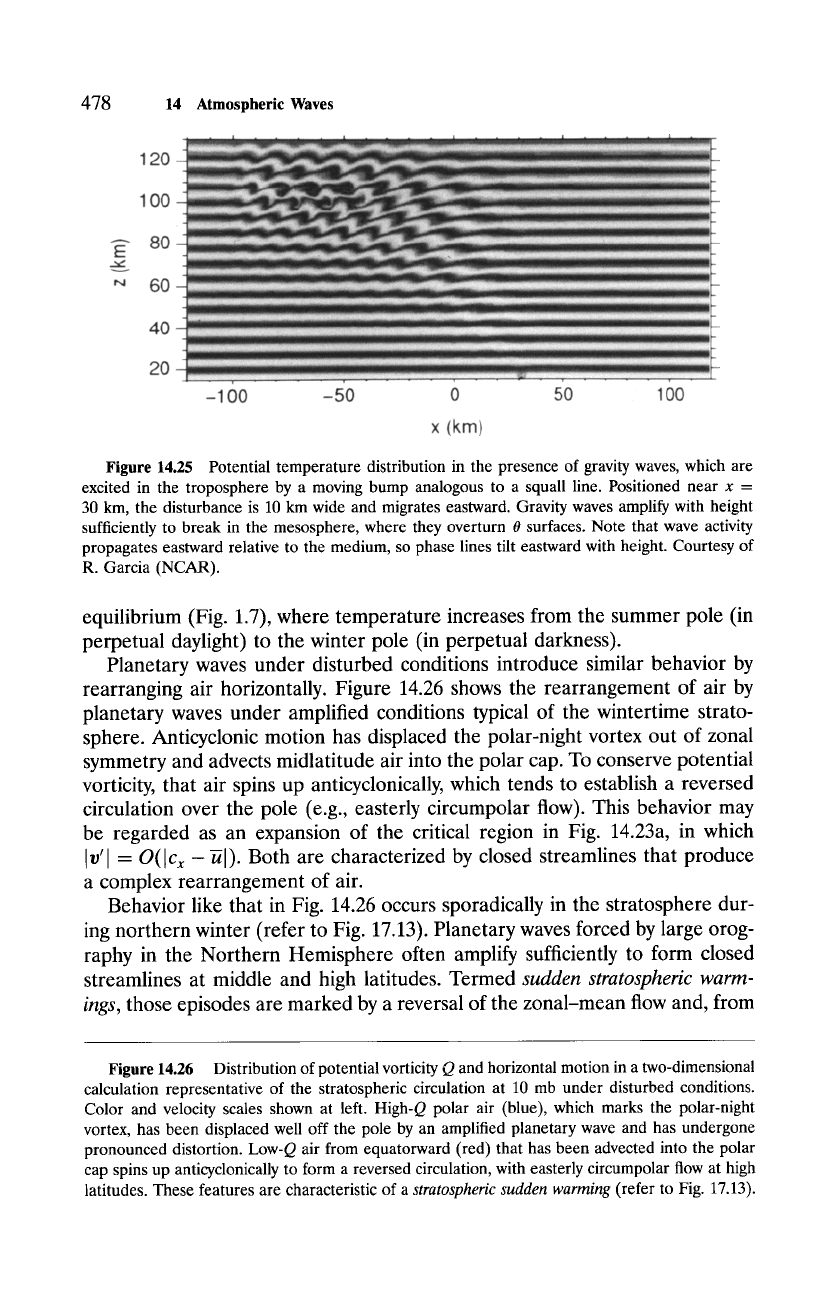
478 14 Atmospheric Waves

120

1 O0

~" 80

- 1 O0 - 50 0 50 1

X (kin)

Figure

14.25 Potential temperature distribution in the presence of gravity waves, which are

excited in the troposphere by a moving bump analogous to a squall line. Positioned near x =

30 km, the disturbance is 10 km wide and migrates eastward. Gravity waves amplify with height

sufficiently to break in the mesosphere, where they overturn 0 surfaces. Note that wave activity

propagates eastward relative to the medium, so phase lines tilt eastward with height. Courtesy of

R. Garcia (NCAR).

equilibrium (Fig. 1.7), where temperature increases from the summer pole (in

perpetual daylight) to the winter pole (in perpetual darkness).

Planetary waves under disturbed conditions introduce similar behavior by

rearranging air horizontally. Figure 14.26 shows the rearrangement of air by

planetary waves under amplified conditions typical of the wintertime strato-

sphere. Anticyclonic motion has displaced the polar-night vortex out of zonal

symmetry and advects midlatitude air into the polar cap. To conserve potential

vorticity, that air spins up anticyclonically, which tends to establish a reversed

circulation over the pole (e.g., easterly circumpolar flow). This behavior may

be regarded as an expansion of the critical region in Fig. 14.23a, in which

I v'l = O(Icx -ul).

Both are characterized by closed streamlines that produce

a complex rearrangement of air.

Behavior like that in Fig. 14.26 occurs sporadically in the stratosphere dur-

ing northern winter (refer to Fig. 17.13). Planetary waves forced by large orog-

raphy in the Northern Hemisphere often amplify sufficiently to form closed

streamlines at middle and high latitudes. Termed

sudden stratospheric warm-

ings,

those episodes are marked by a reversal of the zonal-mean flow and, from

Figure

14.26 Distribution of potential vorticity Q and horizontal motion in a two-dimensional

calculation representative of the stratospheric circulation at 10 mb under disturbed conditions.

Color and velocity scales shown at left. High-Q polar air (blue), which marks the polar-night

vortex, has been displaced well off the pole by an amplified planetary wave and has undergone

pronounced distortion. Low-Q air from equatorward (red) that has been advected into the polar

cap spins up anticyclonically to form a reversed circulation, with easterly circumpolar flow at high

latitudes. These features are characteristic of a

stratospheric sudden warming

(refer to Fig. 17.13).

Problems

479

thermal wind balance, abrupt warming at high latitude~as much as 50 K in

just a few days. Air over the winter pole, which is in perpetual darkness, then

becomes warmer than air in the tropics, which experiences ozone heating. Ac-

cording to Fig. 1.10a, which shows the 10-mb circulation during a stratospheric

warming, this dramatic change in zonal-mean properties actually follows from

a complex rearrangement of air.

In the Southern Hemisphere, orographic features at the earth's surface

are comparatively small, so planetary waves are weaker. For this reason, sud-

den warmings and the disturbed conditions accompanying them are rare in

the Southern Hemisphere. Less disturbed, the Antarctic polar-night vortex

remains closer to radiative equilibrium and therefore much colder than its

counterpart over the Arctic.