Сапожников С.З. Китанин Э.Л. Техническая термодинамика и теплопередача

Подождите немного. Документ загружается.

151

() ()

()

K.,ln

⎥

⎦

⎤

⎢

⎣

⎡

∆+

−=

−

∑

jjj

rrrrr

TrT

Задачу теплопроводности многослойных цилиндрических

стенок чаще всего используют при расчете теплоизолированных

трубопроводов. В связи с этим представляет интерес задача о

критическом диаметре тепловой изоляции. Впервые она

появилась в экспериментах У. Томсона (Кельвина) в 1884 г., а в

1910 г. удалось получить аналитическое решение, совпадающее с

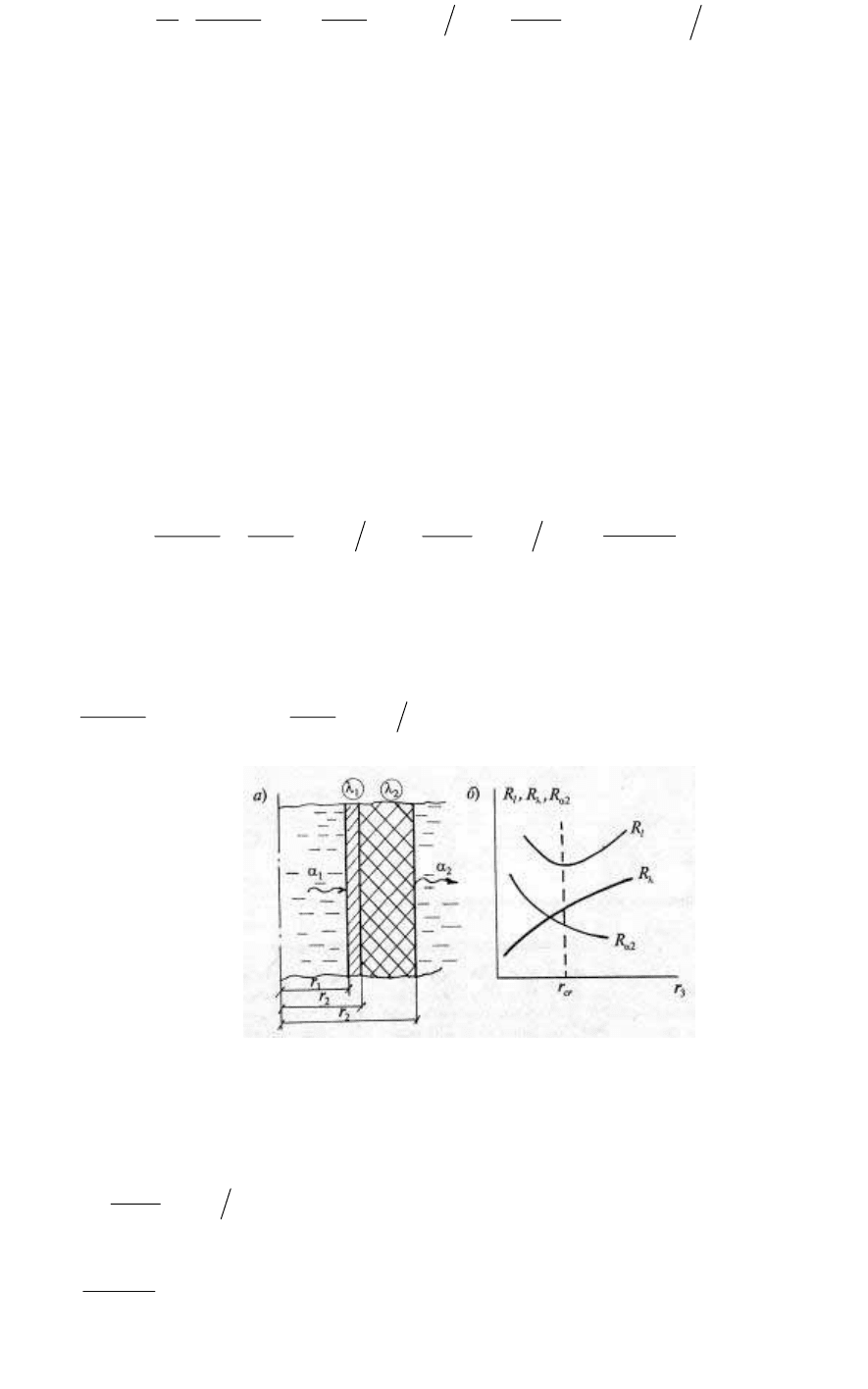
современным. Суть задачи в следующем: двухслойную

цилиндрическую стенку (рис. 83,а) рассматривают в рамках

краевой задачи теплопроводности при граничных условиях III рода.

Полное линейное термическое сопротивление такой стенки

() ()

111

rrrr

При постоянных и заданных

1211

,,,

величина

будет

зависеть только от r

, поскольку члены

()

rrR

λα

радиуса r

не включают.

Рис. 83.

Ясно, что с увеличением значения r

сопротивление

()

rrR

будет увеличиваться, а сопротивление

— уменьшаться (рис. 83,б).

Исследуем

на экстремум по аргументу r

152

323

−

отсюда

()

max

== rr

(2.39)

Значение

называемое критическим диаметром

тепловой изоляции, определяет максимум тепловых потерь с

наружной поверхности цилиндрической стенки.

Из формулы (2.39) следует важный практический вывод: если

< r

, то увеличение толщины изоляции не уменьшает, а

увеличивает тепловые потери! При r

= r

тепловые потери

максимальны и только при r

> r

они начинают снижаться.

Следовательно, при теплоизоляции трубопроводов

необходимо выполнять требование .

Как правило, величину α

определяют условия эксплуатации,

поэтому задача сводится к выбору теплопроводности

теплоизоляционного материала λ

Поскольку в формулу (2.39) не входят ни r

, ни r

соотношения

определяющие кривизну цилиндрической

стенки и толщину внутреннего ее слоя, на величину r

не влияют.

Можно показать, что аналогичные рассуждения справедливы

для любой оболочки, у которой внутренняя поверхность меньше

наружной; вид формул для r

будет при этом зависеть от формы

оболочки.

Шаровая стенка встречается в расчетной практике реже, чем

пластина или стенка цилиндрическая. При решении задачи все

предыдущие рассуждения сохраняют силу. Приведем наиболее

общие формулы: тепловой поток через многослойную шаровую

стенку (рис. 84) при граничных условиях III рода

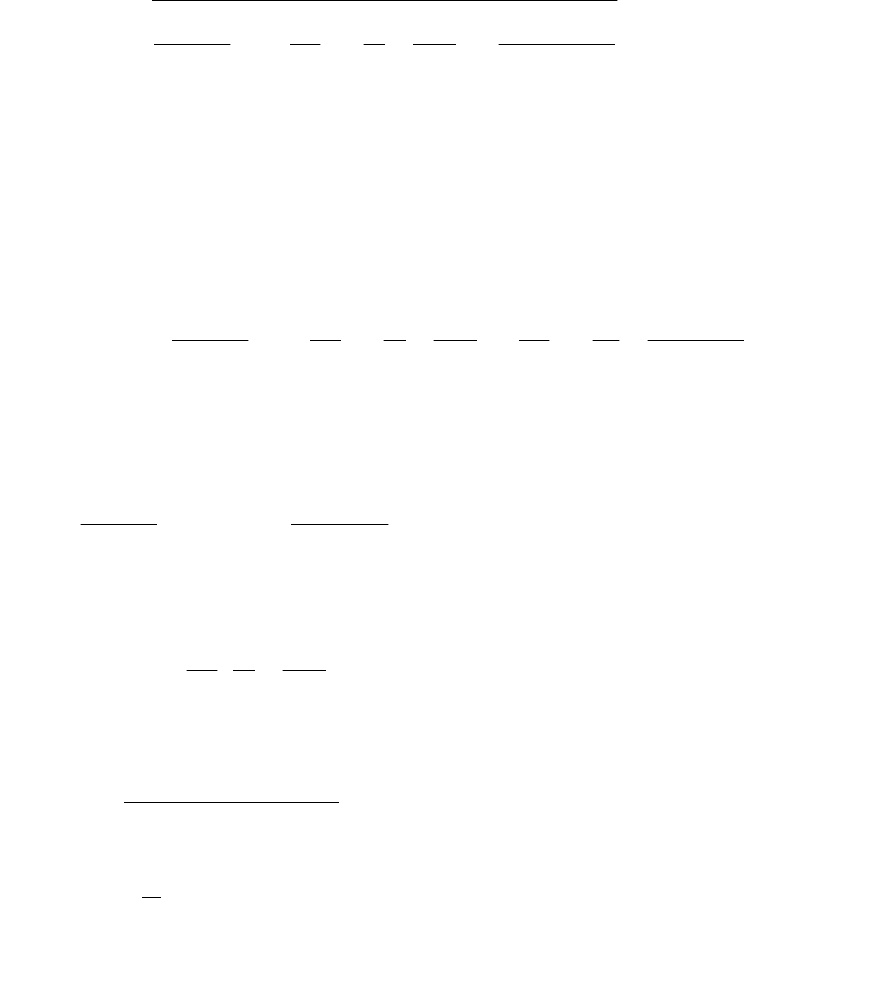
153

()

(

)

Вт,

111

11 +

⎟

⎠

⎞

⎜

⎝

⎛

−

∑

nff

(2.40)

(как видим, в каждом слое стенки температура меняется по закону

гиперболы);

— температура в произвольном слое, отстоящем от центра

шара на расстоянии r,

()

111

⎥

⎦

⎤

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

∆+

−

⎟

⎠

⎞

⎜

⎝

⎛

−

−=

−

∑

jjjiii

rrrrr

TrT

(2.41

)

Не требует пояснений и терминология:

;

αα

— внешние термические сопроти-

вления;

⎟

⎠

⎞

⎜

⎝

⎛

−

Σλ

∑

111

—

суммарное внутреннее термическое

сопротивление слоев;

αΣλα

RRR

— коэффициент теплопередачи;

= —

полное термическое сопротивление шаровой

стенки.

154

Рис. 84.

2.3.2. Теплопроводность оребренных поверхностей

Оребрение поверхности позволяет увеличить тепловой поток

в случаях, когда коэффициент теплоотдачи невысок и не может

быть повышен. Форма теплоотводящих ребер различна (см. рис.

76). Их используют на стенках цилиндров (в ДВС и компрессорах с

воздушным охлаждением); в радиаторах и теплообменниках, на

отопительных приборах, корпусах редукторов и т. д.

Вспомним, что коэффициент теплопередачи через

однослойную пластину

α+λδ+α

где α

, α

— коэффициенты теплоотдачи на внутренней (“горячей”)

и наружной (“холодной”) сторонах пластины, соответственно. Если

155

пренебречь внутренним термическим сопротивлением

R (а

обычно

невелико), то

()

;,min

αα<

αα+

≈

(2.42)

другими словами, коэффициент теплопередачи пластины всегда

меньше наименьшего из коэффициентов теплоотдачи α

и α

увеличить значения α

или α

непросто. Поэтому используют

другой способ: пытаются "развить" поверхность теплоотдачи со

стороны меньших α, выполнить на ней пазы, выступы, стержни —

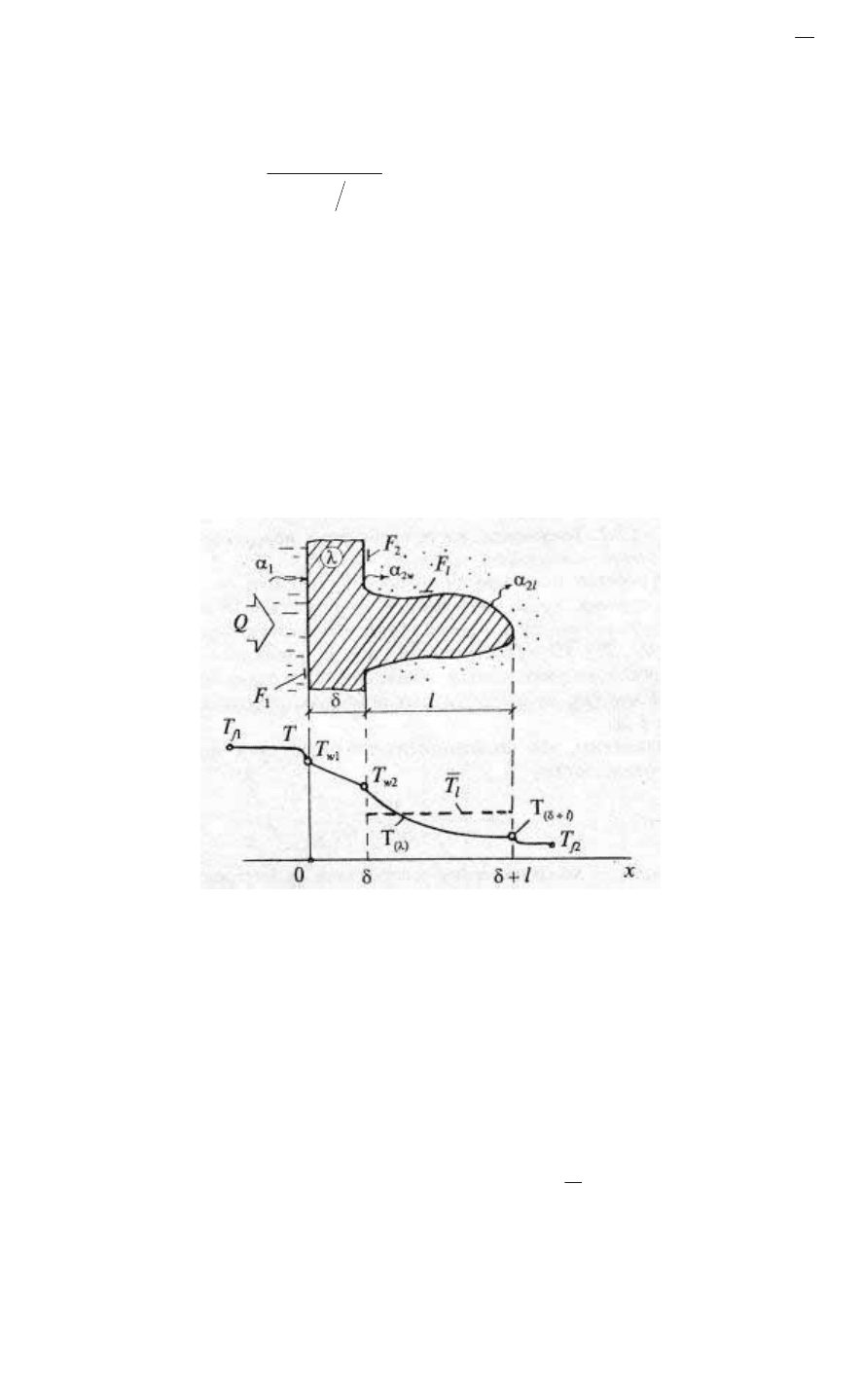
словом, создать теплоотводящие ребра (рис. 85).

Рис. 85.

Пусть через поверхность пластины F

проходит тепловой

поток Q В стационарном режиме этот поток пройдет через сечение

пластины и будет целиком передан среде, омывающей поверхности

и F

. Температура вдоль ребра Т(l) распределена по закону,

который в общем случае неизвестен; будем пока считать, что

средняя по длине ребра l температура равна

T .

Поскольку весь тепловой поток Q передается через

оребренную стенку, можно с некоторыми “натяжками” (определите

сами, в чем они состоят!) записать балансовое уравнение в формe

(

)

;

1111

FTTQ

−

α=

(2.43)

156

()

;

121

FTTQ

−

(2.44)

(

)

(

)

222222 lfllfww

FTTFTTQ

−

(2.45)

где α

, α

— коэффициенты теплоотдачи на поверхностях F

, и F

соответственно. Введем в равенство (2.45) величину

−

=η

(2.44)

которую назовем коэффициентом эффективности ребра.

Численно он равен отношению теплового потока, отдаваемого

реальным ребром (у которого температура

T ) меняется по длине l и

в среднем равна

TT < ), к тепловому потоку, который отдавался

бы "идеальным" ребром с температурой const

TT . Равенство

(2.45) примет вид

(

)

(

)

()()

1222122

2222222

FTTFTT

FTTFTTQ

fwfw

lfwlfww

−α=−

⎟

⎠

⎞

⎜

⎝

⎛

α+α=

−

−α=

(2.46)

где

α — приведённый коэффициент теплоотдачи (условная

величина, смысл которой ясен из формулы (2.46)):

ηα+α=α

Из равенств (2.43), (2.44) и (2.46) следует,

что

()

1211

FTTkF

−=

α+λδ+α

−

где

— приведённый (и тоже условный) коэффициент

теплопередачи:

α+λδ+α

(2.47)

Уравнения (2.47) и (2.42) сходны по структуре; можно

считать, что теплопередача станет интенсивнее только при

157

>η

(2.48)

Пусть, например,

,5,0

.9,0=

В этом

случае .5

Пусть, кроме того,

(

)

Вт,/Км10

⋅=

−

()

(

)

Вт./Км10

Вт,/Км10

⋅=

−−

При таких условиях коэффициент теплопередачи на гладкой

пластине (при

w22

α=α ), согласно уравнению (2. 42),

К),Вт/(м3333

101010

444

⋅=

−−−

а приведенный коэффициент теплопередачи через оребренную

пластину, на основании равенства (2.47),

(

)

К)Вт/(м4545

5,09,0105,0101010

4444

9,0

k >⋅=

⋅⋅+⋅++

−

−−

=η

следовательно, при η = 0,9 оребрение пластины

целесообразно. Если же η = 0,1, то

,К)м/(Вт1051,0105,010

2444

2 w

α=⋅=⋅⋅+⋅=α поэтому kk =

=η 1,0

оребрение выгоды не дает (хотя размеры и массу конструкции

увеличивает!).

В случае же, если η = 0,05,

,К)м/(Вт1075,0505,0105,010

2444

2 w

α<⋅⋅=⋅⋅+⋅=α

(

)

:К)Вт/(м3000

1075,01010

444

05,0

kk <⋅=

⋅++

−

−−

=η

оребрение не увеличивает, а уменьшает тепловой поток Q.

Поэтому надо очень тщательно проектировать ребро,

стремясь к более высоким значениям η. Но как этого добиться?

158

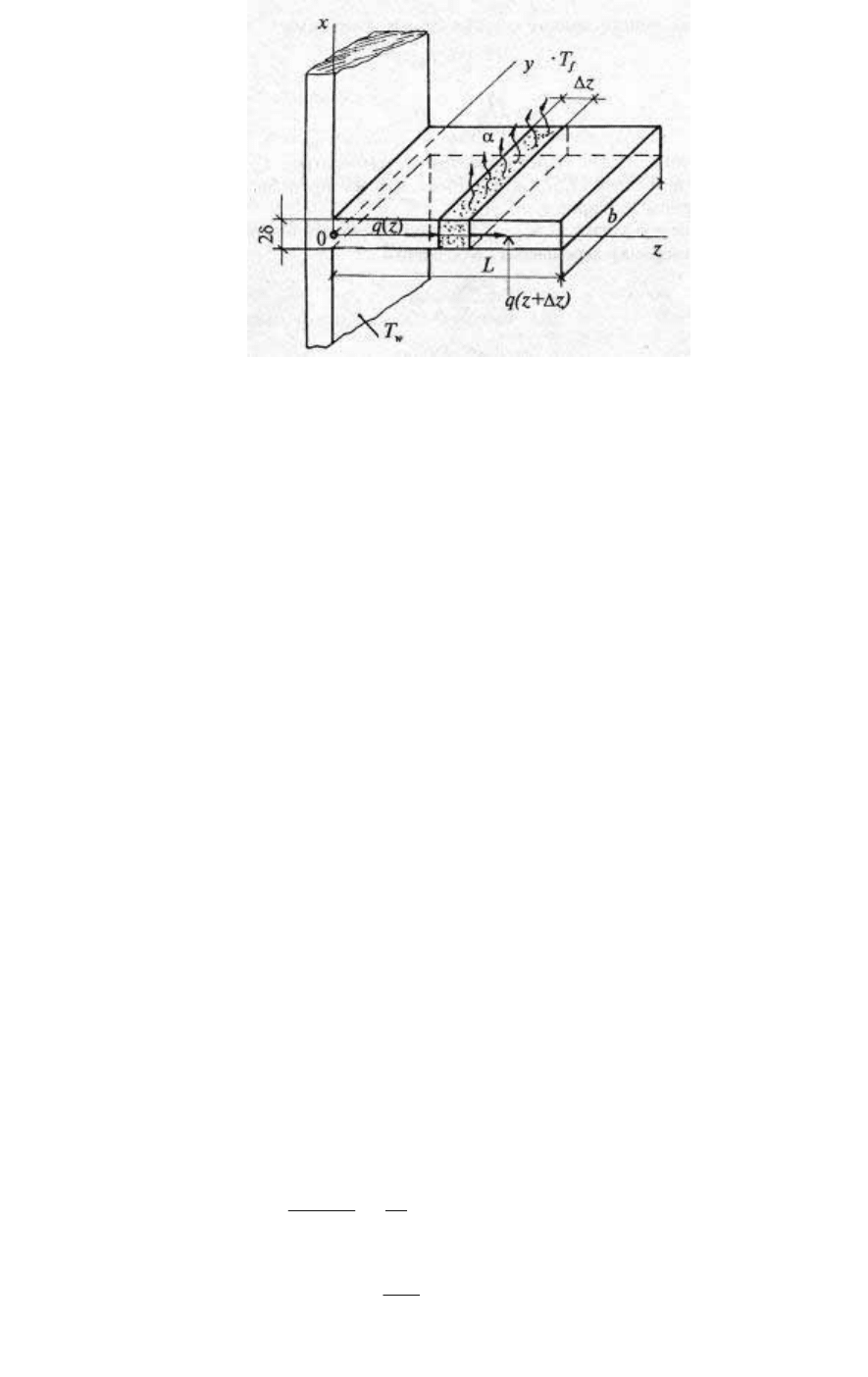
Рис. 86.

Рассмотрим задачу теплопроводности для ребра постоянного

сечения (рис. 86), полагая, что:

— температура ребра T(z) меняется только вдоль оси z;

— теплота передается в окружающую среду только с верхней

и нижней поверхностей ребра, площадь каждой из которых равна

l×b;

— коэффициент теплоотдачи на этих поверхностях постоянен

и равен α, а плотность теплового потока

[

]

,)()(

TzTzq −

где

— температура окружающей среды.

Выделим в ребре элемент шириной ∆z, на левой границе

которого тепловой поток имеет плотность

,)(zq

а на правой —

плотность ).()( zqzzq <∆+ Уравнение теплового баланса на

выделенном элементе имеет вид

(

)

,0)2(2)(2)(

−

∆

−

∆+−δ

TTzbbzzqbzq

где T — температура на поверхности полосы шириной ∆z. Разделив

все члены на ,2

b∆δ перейдем к пределу при ∆z →∞:

(

)

)(

−

∂

−

(2.49)

но по закону Фурье ,)(

∂

λ−= поэтому уравнение (2.49) примет

вид

159

()

;

−

λδ

∂

(2.50)

его надо решать вместе с граничными условиями

;

(2.51)

.0=

∂

=Lz

(2.52)

Условие (2.51) задает постоянную температуру T

у корня

ребра, а условие (2.52) напоминает, что мы пренебрегли

теплообменом на торце z = L.

Краевую задачу (2.50)-(2.52) удобнее решать в обобщенных

(безразмерных) переменных. Обозначим

Bi.

;;

;

Θ=

−

∗

Здесь Θ — безразмерная избыточная температура; Z, L* —

безразмерные текущая координата и длина ребра, соответственно,

а величина Bi (число Био) имеет особый физический смысл.

Поскольку

число Био характеризует соотношение термических сопротивлений:

внутреннего R

и внешнего R

. При Вi → 0, R

→ 0 ребро в

поперечном сечении почти изотермично, температура меняется

только по его длине. При Вi → ∞, R

→ 0 поверхность ребра имеет

практически ту же температуру, что и жидкость, а изменения

температуры происходят почти целиком в сечении ребра.

Запомним, что число Био “появляется” только там, где заданы

граничные условия III рода.

160

Приведем уравнение (2.50) к безразмерному виду:

,Bi

∗

⋅Θ=

∂

Θ∂

(2.53)

его общее решение

(

)

(

)

,BiexpBiexp

∗∗

⋅+⋅=Θ LZCLZC

(2.54)

где С

, С

— постоянные, зависящие от граничных условий; их

определяют соотношения (2.51) и (2.52), также представленные в

безразмерной форме:

.0,1

∂

=Θ

Решение уравнения (2.54) примет вид

()

[

]

(

)

Bich

Bi1ch

∗

⋅

⋅−

=Θ

(2.55)

где

−

— гиперболический косинус аргумента u.

Тепловой поток, отводимый от ребра,

(

)

(

)

,Bith

∗∗

⋅−

λδ

⋅= LTT

(2.56)

где

−

=th

— гиперболический тангенс аргумента и.

Для идеального (бесконечно теплопроводного) ребра

тепловой поток равен

(

)

TTbQ −δλ=

∗

поэтому коэффициент эффективности ребра

()

(

)

()

(

)

.Bith

Bith

∗

∗∗

∗

⋅

−α

⋅−

λδ

⋅

==η L

TTbL

LTT

(2.57

)