Сапожников С.З. Китанин Э.Л. Техническая термодинамика и теплопередача

Подождите немного. Документ загружается.

161

Графики функций

(

)

(

)

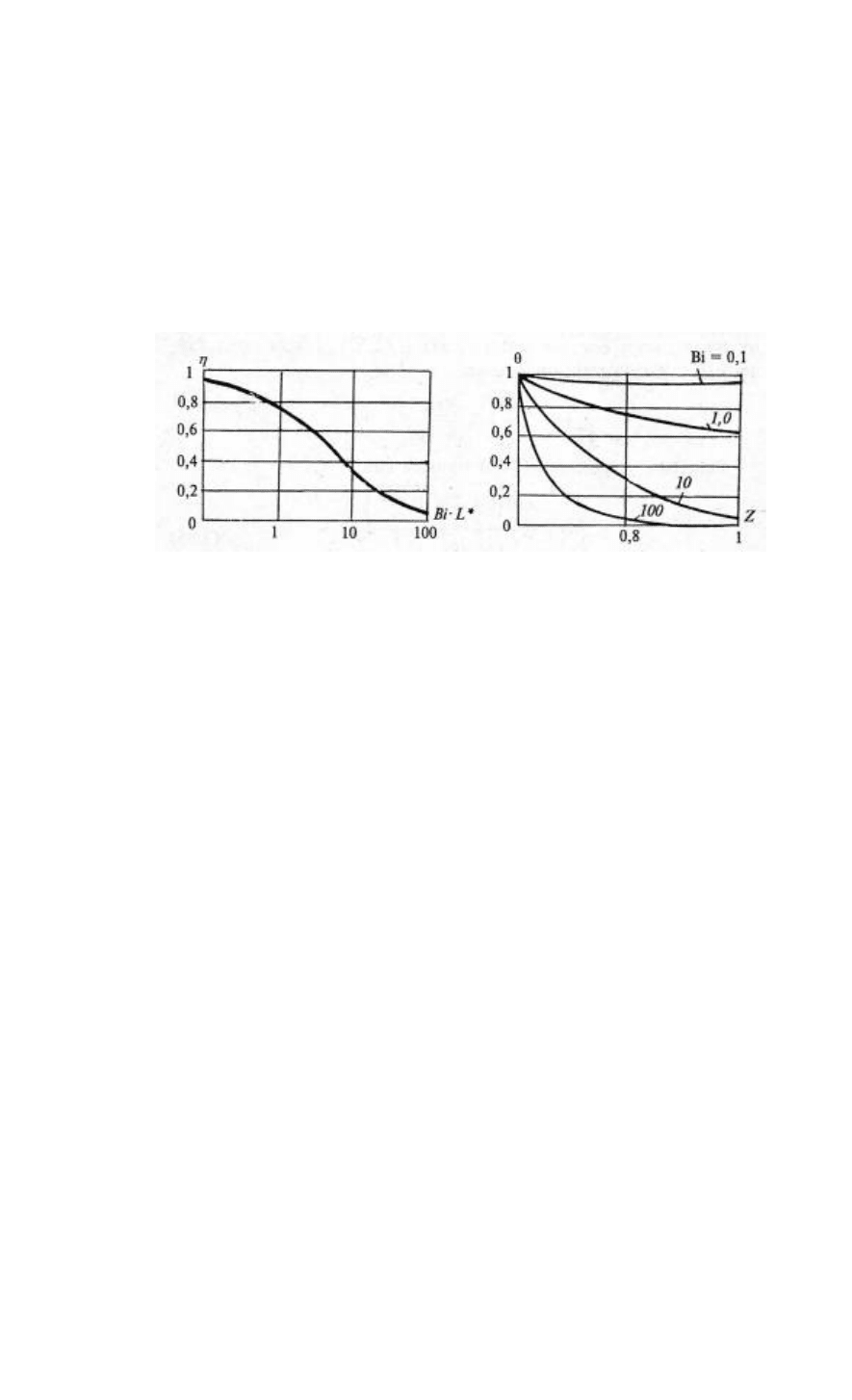
Bi,иBi ZL Θ⋅η

∗

представлены на рис.

87.

Мы рассмотрели только одну из задач, связанных с

оребрением поверхностей теплообмена. В справочной литературе

таких задач приведено очень много, при этом обоснован выбор

ребра с оптимальной формой сечения, приведены данные по

кольцевым, стержневым и другим ребрам (см. рис. 76,а,б,в).

Рис. 87.

Итак, для теплового расчета оребрения необходимо:

1) сформулировать задачу: оценить значения α, размеры,

обусловленные конструкцией, а в ряде случаев также и материал

ребра (т. е. задать λ);

2) по справочным данным определить вид функций (2.55),

(2.56) и (2.57), после чего уточнить размеры, выбор материала и

рассчитать все необходимые величины, в первую очередь — Q.

При расчете транспортных систем могут возникнуть и другие

задачи, например:

экономия массы оребрения, что сводится как к выбору более

легких материалов (алюминия вместо меди или латуни), так и к

оптимизации формы ребер;

оценка предельно допустимых значений температуры

оребрения по соображениям пожаробезопасности и удобства

эксплуатации (желательно, в частности, чтобы в зоне обслуживания

агрегатов температура оребрения не превышала +60 °С);

обеспечение расчетного значения коэффициента

теплопередачи: нельзя ставить ребра “слишком часто”, чтобы их

162

поверхность не покрылась грязью; из набегающего потока воздуха

на оребрение могут попасть насекомые и т. д.

Надо помнить, что расчет оребрения — многовариантная

(оптимизационная) задача, требующая творческого подхода и не

имеющая “единственно верного” решения. Целевую функцию

(например, Q) определяют с учетом добавочных ограничений, речь

о которых шла выше.

2.4. НЕСТАЦИОНАРНАЯ ТЕПЛОПРОВОДНОСТЬ

Тепловые процессы в транспортных системах могут

существенно зависеть от времени. Запуск и остановка двигателей,

насосов и других агрегатов, предпусковой прогрев двигателя,

отопление салона, отсека или кабины, действие экстремальных

факторов (огня, резкого охлаждения в воде) — далеко не все

причины, заставляющие обратиться к расчету нестационарной

теплопроводности элементов конструкции, отдельных агрегатов и

машины в целом.

Математически такая задача сводится к решению

дифференциального уравнения Фурье (2.11) вместе с условиями

однозначности, соответствующими нестационарной природе

процесса.

Со времен Фурье методы решения краевой задачи

теплопроводности развивались весьма успешно; к настоящему

времени создана аналитическая теория теплопроводности,

позволившая решить множество инженерных задач. В последние

10–20 лет активно развиваются численные методы, пригодные для

решения задач практически любой сложности.

Аналитический аппарат теории теплопроводности сложен и

громоздок, а программирование задач для численного решения

требует больших затрат времени; оба пути доступны лишь

теплотехникам-профессионалам.

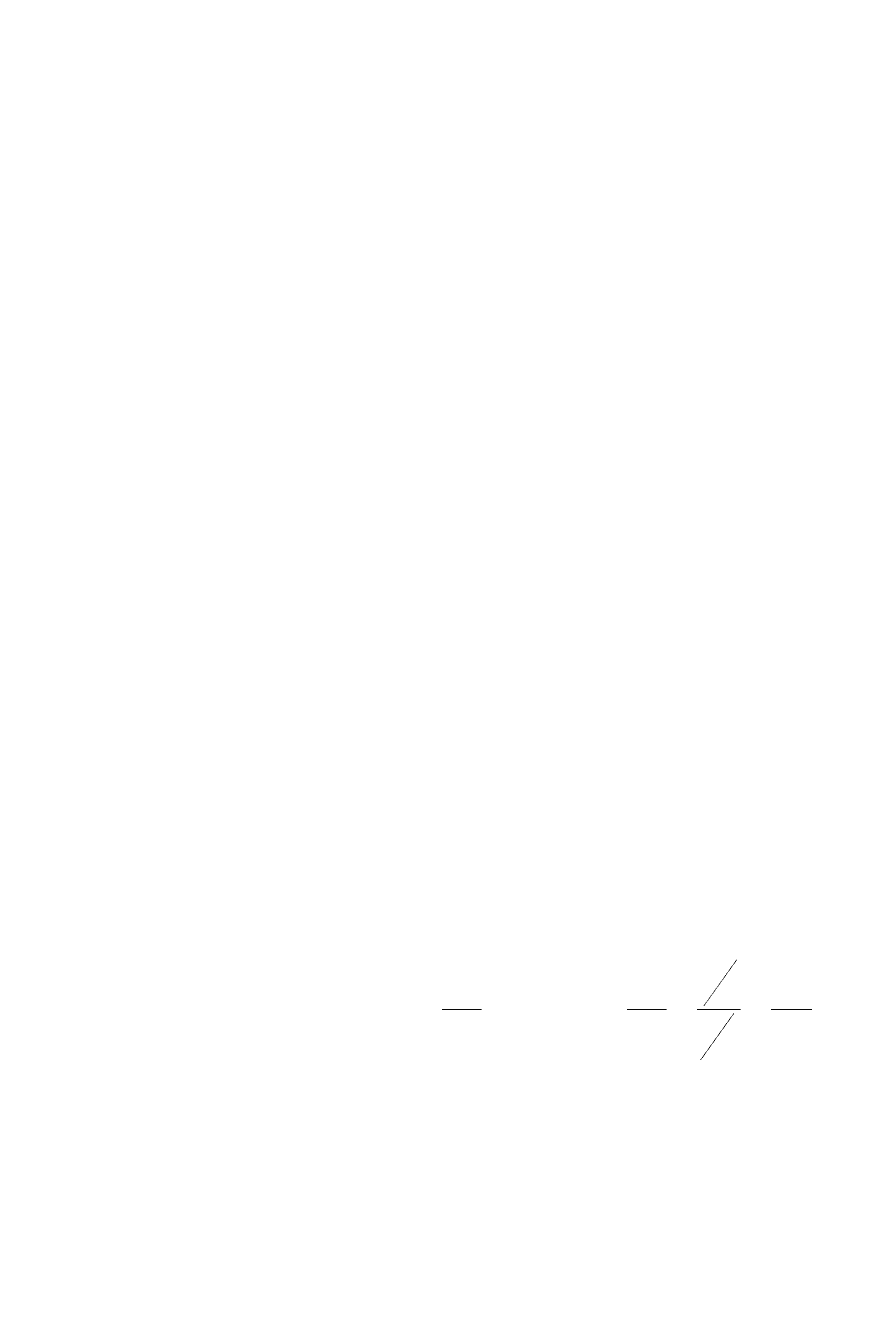
163

Тем не менее, в инженерных расчетах можно и нужно

использовать достаточно простые формулы, обращаясь при

необходимости к справочной литературе и помощи специалистов.

В разд. 2.4 речь пойдет об аналитических решениях

линейного равнения теплопроводности, широко используемых в

расчетах плового состояния твердых тел. Набор таких решений

может асширяться в зависимости от конкретных технических задач.

2.4.1. Теплопроводность термически тонких тел

К термически тонким относят тела, у которых в любой

момент нагрева или охлаждения температура мало меняется по

координатам. Простейший пример — нагретое докрасна

бритвенное лезвие, которое опускают в стакан с водой или

охлаждают на воздухе. В его сечении (0,08…0,1 мм) температуры

всех точек почти одинаковы. Лезвие охлаждается буквально на

глазах: о температуре можно судить по изменению цвета

(например, с помощью оптического пирометра).

Именно в такой постановке, при граничных условиях III рода,

мы и рассмотрим задачу теплопроводности для термически тонких

тел. Ясно, что тело будет почти изотермичным, если его внутреннее

термическое сопротивление R

= R/λ (R — обобщенный размер

тела) окажется заметно меньшим, чем внешнее термическое

сопротивление R

= R/α, т. е.

.1<<

Но Bi,

поэтому термически тонким назовем тело, у которого

1.Bi

(2.58)

Пусть однородное тело, удовлетворяющее условию (2.58),

погружено в жидкость с температурой T

, причем коэффициент

теплоотдачи α = const (рис. 88).

164

Рис. 88.

Теплофизические свойства тела (λ,ρ,с), его объем V и

поверхность F заданы, а температура, вследствие исходного

допущения, меняется только во времени: Т = T(τ).

В соответствии с первым началом термодинамики, отвод

теплоты в окружающую среду уменьшит энтальпию тела:

[

]

.)(

)(

TTF

cV −τα=

τ∂

∂

ρ−

(2.59)

Поскольку температура Т

= const, а

[

]

,)()(

TTT −τ∂=

∂

введем новую переменную — избыточную температуру

.)(

−

=ϑ

Зададим, кроме того, начальную температуру тела Т

и ее

аналог — начальную избыточную температуру

−

=τ

(2.60)

Решение дифференциального уравнения (2.59) при начальном

условии (2.60) имеет вид

)(

τα

−

τϑ

(2.61)

Заметим, что

;

⋅

λρ

τλα

τα

165

но, как показано в разд. 2.2.5, ,R

= поэтому

Fo,Bi

⋅=

⋅

τλ

⋅

τα

где

aτ

= — безразмерный параметр, называемый числом

Фурье (иногда его называют обобщенным временем).

Таким образом, уравнение (2.61) принимает безразмерный вид

FoBi⋅−

=Θ e

(2.62)

где

)(

τϑ

=Θ — безразмерная избыточная температура.

Тепловой поток в момент τ можно рассчитать по закону

Ньютона

[

]

);()()(

−

α=τ FTTFQ

(2.63)

откуда в соответствии с равенством (2.62),

FoBi

)(

⋅−∗

ϑα

= e

(2.64)

— безразмерный тепловой поток от тела к жидкости.

Количество теплоты Q

(τ), отданное телом с начала процесса

до момента τ, определяется интегрированием уравнения (2.63):

∫∫

⋅−

τϑα=ττ=τ

FoBi

,dd)()( eFQQ

или, в безразмерной форме,

(

)

)(

)Fo(

FoBi

⋅−

⋅−=

ϑτα

⋅−

∗

(2.65)

Сопоставление формулы (2.62) с точными решениями

показывает, что при Вi < 0,1 ошибка в определении температуры

редко превышает 5%. При Вi > 0,1 следует обратиться к более

точным методам — или смириться с довольно высокой

погрешностью расчета по формулам (2.62)–(2.65).

166

Условие (2.58) используют и в случае, когда вместо твердого

тела речь идет об объеме хорошо перемешиваемой жидкости

(например, масла в картере двигателя). Если при этом необходимо

описать нестационарный отвод теплоты в окружающую среду, то

уравнения (2.62)–(2.65) сохраняют силу.

2.4.2. Теплопроводность полуограниченного тела и

стержня

Полуограниченным в разд. 2.2.5 мы назвали достаточно

большое тело с одной плоской поверхностью, к которой подводится

теплота (см. рис. 75, а). Температура такого тела обычно меняется

только вдоль оси х, поэтому уравнение теплопроводности будет

одномерным:

∂

τ∂

∂

(2.66)

Начальное распределение температур будем считать

равномерным:

.)0,(

TxT

(2.67)

Условия полуограниченности задают температуру и

плотность теплового потока при х →∞:

,),(

∞

(2.68)

откуда ,0

),(

∂

∞

∂

т. е. на достаточно большой “глубине” х

температура тела равна начальной, а тепловой поток — нулю.

Уравнение (2.66) удается решить, если кроме условий (2.67) и (2.68)

ввести граничные условия на свободной поверхности х = 0.

Рассмотрим вначале вариант, когда температура границы х = 0 в

начальный момент скачком меняется от Т

до Т

, а затем

поддерживается постоянной (граничные условия I рода):

.),0(

(2.69)

Задача (2.66)–(2.69) имеет решение

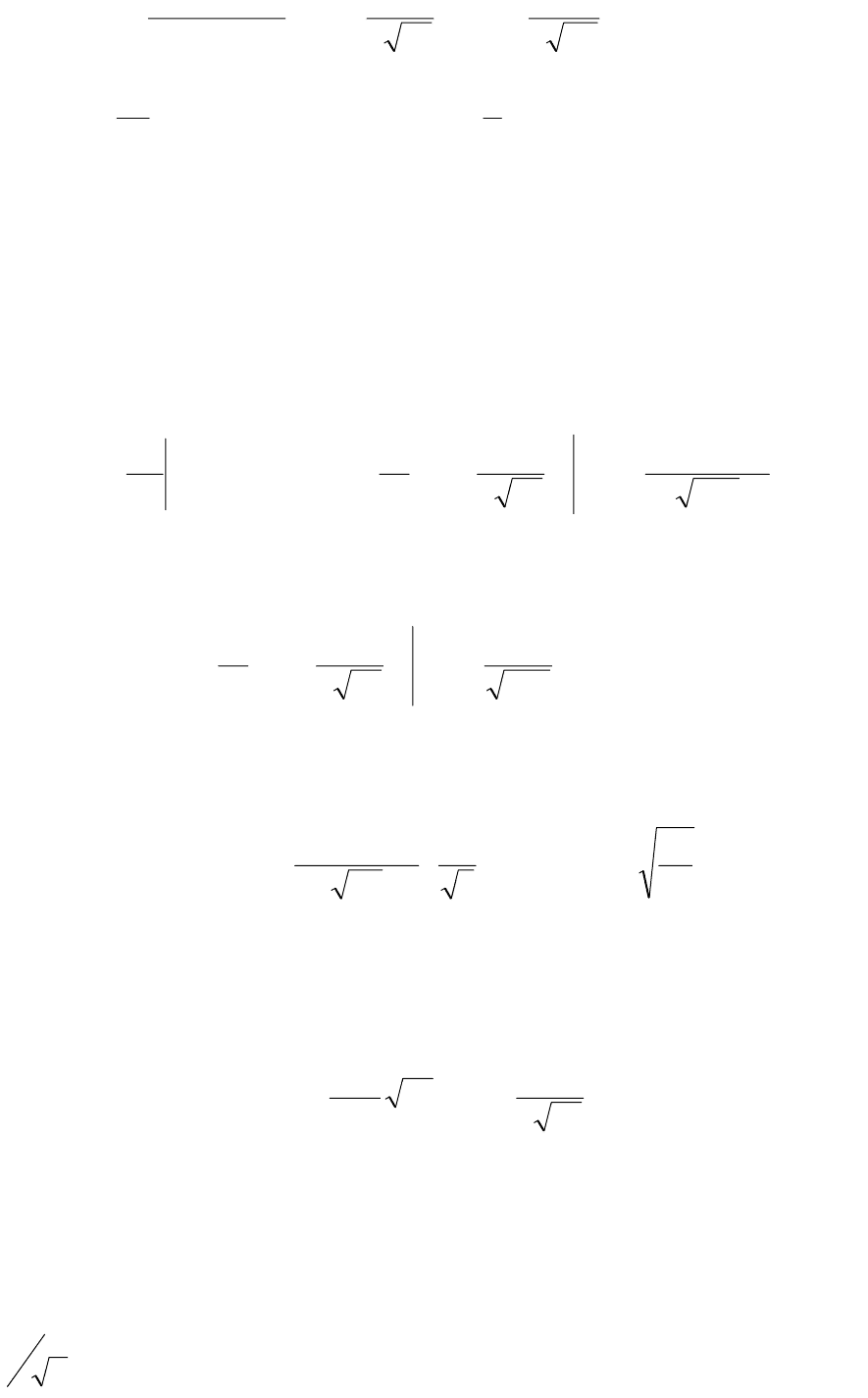
167

Fo2

erf

),(

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

−

TxT

(2.70)

где

aτ

— число Фурье; ueu

)(erf

∫

−

— функция ошибок

Гаусса для аргумента u (рис. 89)(лат. erratum + лат. functio). Уже

при u ≈ 2,7еrf(u) = 0,9999... Это означает, что температурное

возмущение ослабевает по “глубине” х достаточно быстро, а

неравномерность поля температуры тем сильнее, чем меньше

значение τ.

Плотность теплового потока на поверхности х = 0

)(

erf)()(

τπ

−λ

⎥

⎦

⎤

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

∂

−λ−=

∂

λ−=

(2.71

)

поскольку, как известно,

erf

τπ

⎥

⎦

⎤

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

∂

Общее количество теплоты, переданное в глубь тела с

поверхности х = 0 за время τ,

.)(2

)(

d)()(

−λ=

−λ

=ττ=τ

∫∫

(2.72)

Пусть теперь на поверхности х = 0 задана плотность

теплового потока q(τ) = q

= const (граничные условия II рода);

тогда

ierfc

),(

⎟

⎠

⎞

⎜

⎝

⎛

⋅τ

=−τ

TxT

(2.73)

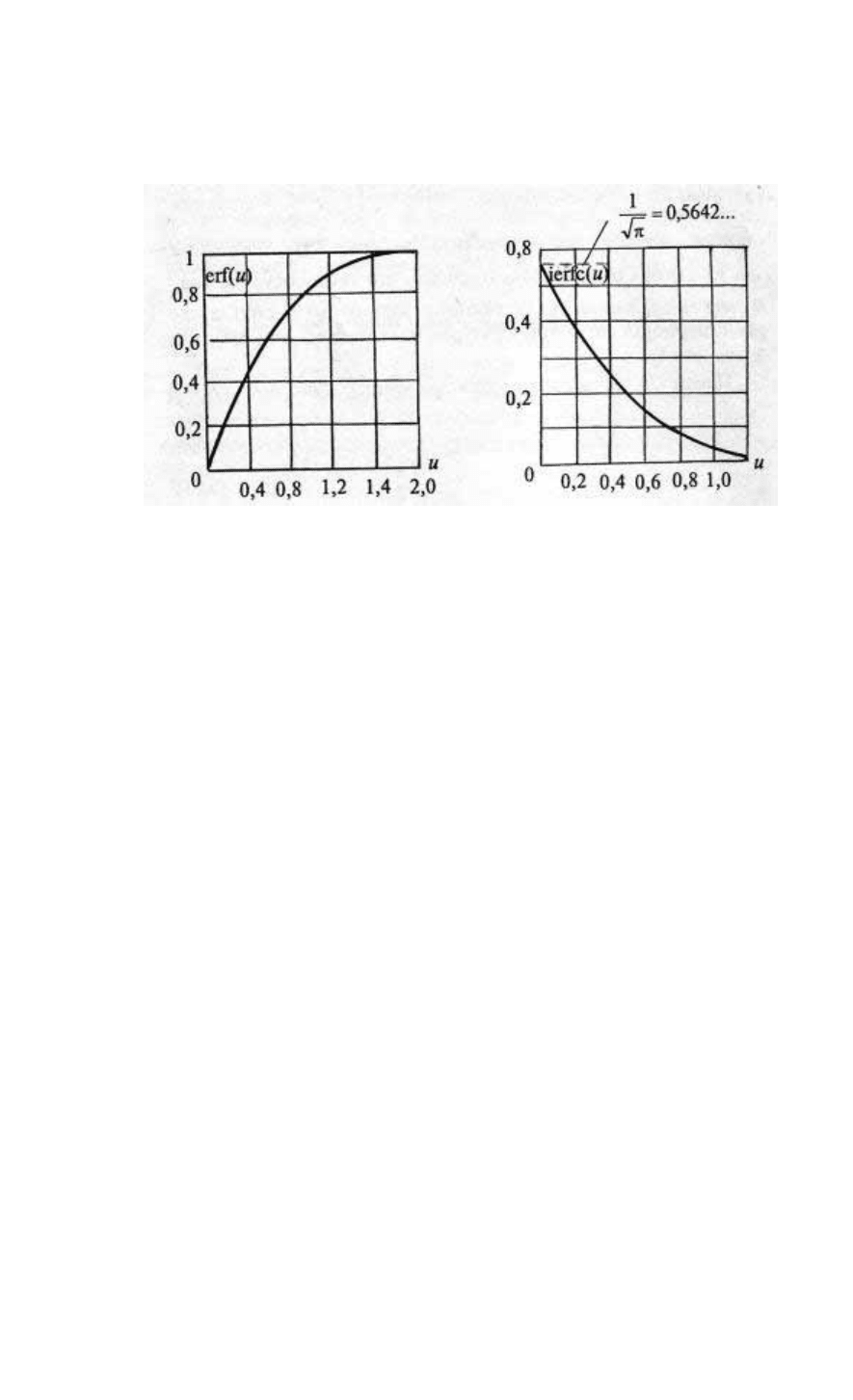
где

() ()

[]

uuu

derf1ierfc

∫

∞

−= — специальная функция аргумента u

(рис. 90)(сокр. ierf + лат. complementum — интеграл дополнения

функции ошибок), принимающая при u = 0 значение

...5642,0

≈

и уже при u = 2,0 падающая почти до нуля.

168

Поскольку в этом случае величина q

задана, общее количество

теплоты, переданное с поверхности х = 0 за время τ,

.)(

(2.74)

Рис. 89. Рис. 90.

Уравнение (2.66) — одномерное, поэтому все результаты,

полученные для полуограниченного тела, можно использовать

и для полуограниченного стержня, у которого боковая

поверхность теплоизолирована (см. рис. 75,б).

В справочной литературе приводят решения задачи

теплопроводности для полуограниченных тел и стержней при

разных граничных условиях; все они выражаются через

специальные функции, родственные функции ошибок Гаусса.

Отметим, что граничные условия I и II рода на поверхности

полуограниченного тела принципиально различны. Сравнение

формул (2.70) и (2.73) показывает, что при T

= const поле

температуры стремится к стационарному (когда Т(х,∞) = T

), а

условие q

= const при τ→∞ приводит к неограниченному росту

температуры Т(х, τ). Фактически, конечно, ограничения на такой

рост накладывают реальные свойства материала: он плавится,

испаряется и т. д. На практике по мере нагрева могут изменяться

граничные условия: с поверхности в область х < 0 все больше

теплоты будет отводиться излучением, путем конвективного

теплообмена и т. д. Однако физически результат Т(х,∞)→∞ не

является неожиданным. Вспомним, что уравнение первого начала

169

(2.6) при Q

=0 имеет форму –Q

= ∆H , а при τ→∞ принимает вид

= 0. С другой стороны, по определению,

,dd

∫∫

τ=

FqQ

поэтому условие

0dd =τ

∫∫

является обязательным для всех

случаев, когда поле температуры при τ→∞ становится

стационарным. При нагреве полуограниченного тела тепловым

потоком плотностью q

= const на всей поверхности х = 0 отвод теп

лоты “не предусмотрен”, 0dd ≠τ

∫∫

Fq и стационарное

распределение температуры недостижимо.

2.4.3. Нагрев и охлаждение пластины, цилиндра и шара

В разд. 2.3.1 мы рассмотрели стационарную

теплопроводность пластины, цилиндрической и шаровой стенок

при граничных условиях I и III рода. В начальной стадии процесса,

когда ,0≠

τ∂

∂

решение таких задач значительно усложняется.

Для решения нестационарной краевой задачи Фурье

используют приемы, которые слишком громоздки, чтобы их могли

применить инженеры-транспортники. Поэтому рассмотрим лишь

общий вид решений и остановимся на некоторых важных частных

случаях.

Пусть пластина из материала с известными

теплофизическими свойствами (λ, ρ, с) имеет толщину 2δ (рис. 91).

В начальный момент температура пластины равна Т

, а затем

пластину погружают в среду с температурой Т

, что приводит к

теплообмену по закону Ньютона при коэффициенте теплоотдачи,

равном α. Краевая задача Фурье примет вид

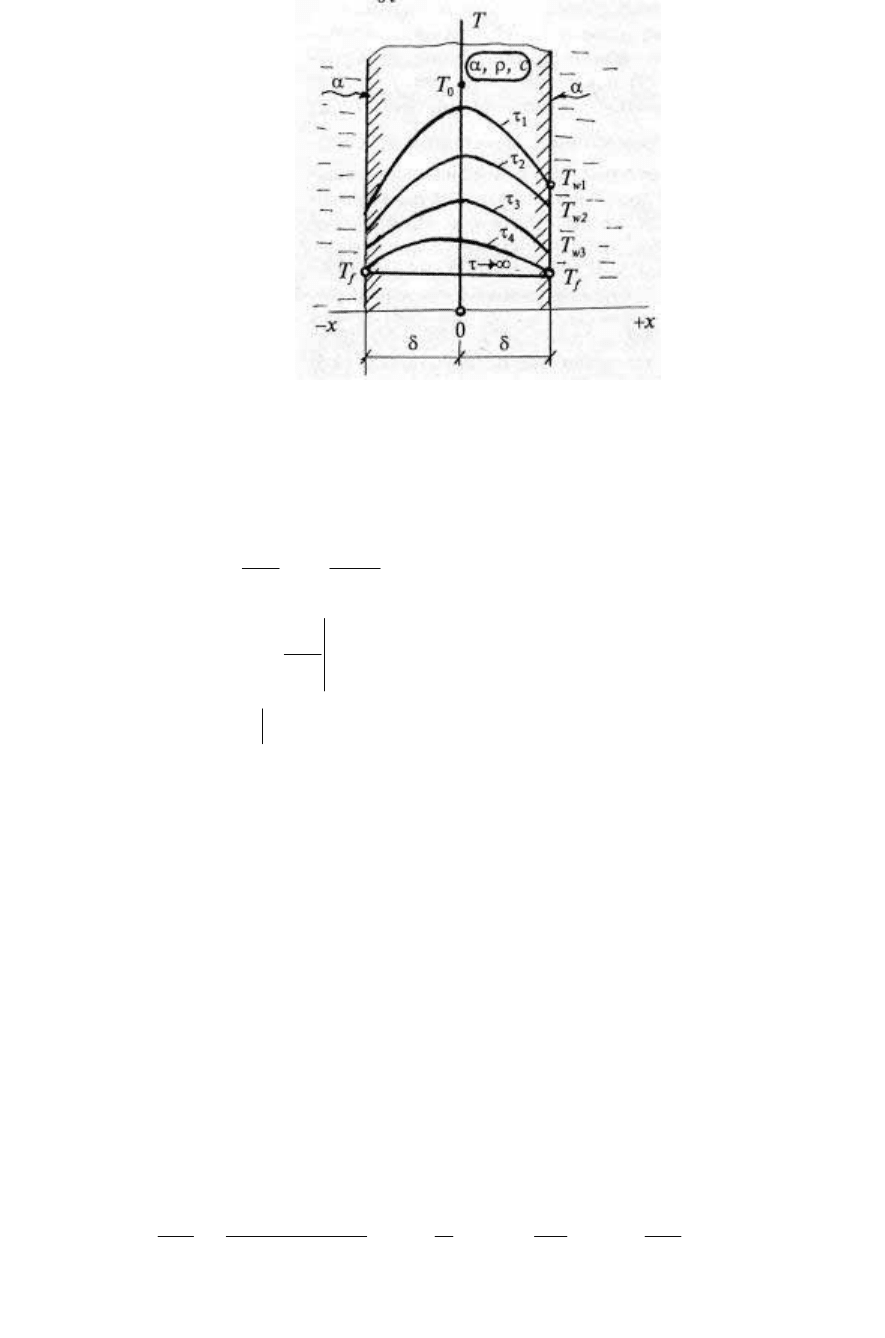
170

Рис. 91.

()

;

−α=

∂

λ−

∂

τ∂

∂

=τ

δ±=

(2.75)

(2.76)

(2.77)

(условие (2.76) означает, что пластина охлаждается симметрично).

Ясно, что в любой момент τ > 0 температуры T(х) в

поперечном сечении пластины и Т

на ее поверхности будут

меняться, пока при τ→∞ не станут равными Т

. На рис. 91 показаны

кривые T(τ) для условно выбранных значений времени τ

< τ

Задачу (2.75)–(2.77) принято записывать в безразмерной

форме. Если положить что

,Bi;Fo;L;

),(

;;),()(

αδ

−

−τ

=Θ

−

−τ=τϑ

TxT

TTTxT

то уравнение (2.75) преобразуется так: