Щелкачев В.Н. Основы и приложения теории неустановившейся фильтрации: Часть 1

Подождите немного. Документ загружается.

гаемых, заключенных в квадратных скобках равенства (11.46), обра

щается в нуль при ? = оо. Раскрывая неопределенность по правилу

Лопиталя, для чего приходится использовать правила дифференци

рования кратных интегральных дополнительных функций-ошибок —

см. (П40), обнаруживаем, что, как и следовало ожидать:

(11.50)

По поводу зафиксированного в равенстве (11.50) неограничен

ного увеличения понижения давления во второй зоне см. еще

соответствующее пояснение в § 2 главы Ш.

Заметим, что предельным переходом можно от рассматриваемого

объемного стока перейти к плоскому поверхностному стоку. Для

этого надо принять, что длина L объемного стока стремится к нулю.

Действительно, положим, например, в формуле (11.47) L * 0.

Раскрывая получившуюся неопределенность по правилу Лопиталя,

найдем:

[ДР2 (Д. 01 l=o -

L=Q

G aи /j*

VjTaJfc

(11.50a)

Правая часть формулы (11.50a) совпадает, как и следовало

ожидать, с правой частью формулы (4.35), выведенной в § 2 главы 4,

для понижения давления на поверхности плоского стока.

Дифференцируя по х равенство (11.46), определим градиент

понижения давления:

ЭДp2(x,f) QcHVitff. , х-а . a + L-x

= ‘ ег&Ж - J erfc^ 7

(11.51)

Полагая в равенстве (11.51) х = а + —, получаем:

ЭЬрг (х, о

Эк L

х = а+2

= 0, 0 <f<°o,

(11.52)

т.е., благодаря симметрии притока жидкости к объемному стоку с

двух сторон, градиент давления в середине стока всегда равен нулю.

На границе II и I зон, т.е. при х = а, градиент понижения

давления определится по формуле (11.51) так:

Эх

Полагая в равенстве (11.53) f—>«>, переходя к пределу и опять

раскрывая неопределенность по правилу Лопиталя, получаем

величину максимального градиента давления при х = а:

Э Ар2 (х, t)

дх

х = а

t - оо

Qc ^

2а* •

(11.54)

Основываясь на равенствах (11.46)—(11.54), на рис. 11.4 схема

тично изображены пьезометрические линии во второй зоне потока

в различные моменты t = 0, th t29t3. При х = а + ^г касательные ко

всем этим линиям горизонтальны.

Продифференцируем равенство (11.46) по времени:

ЭДр2 (X, t) Qc\iK

2Vitf

oLk

1-2

i2 erfc

a +L-x

2VKf

+ i2 erfc

2VkT

ч . a + L -л: , 4 . * x-a

(a + L - x)« e r f c - ^ ^ + (* - a)« e r f c ^ -

(11.55)

Примем в равенстве (11.55) t = 0 и раскроем неопределенность;

получим:

Э Др2 (дс, *)

г=о

aLfc

(11.56)

Т.е. оказывается, что для всех точек II зоны линии всех графиков

зависимости понижения давления Ар2 от времени t будут иметь в

начале координат (при t = 0) общую касательную с угловым

Qc\ik

коэффициентом - Учитывая этот факт и равенства (11.46)—

(11.50), на рис. 11.5 схематично изображены графики зависимости

понижений давления от времени на границе II зоны (при х = а),

в ее середине (при х = а + —) и в произвольной промежуточной

точке.

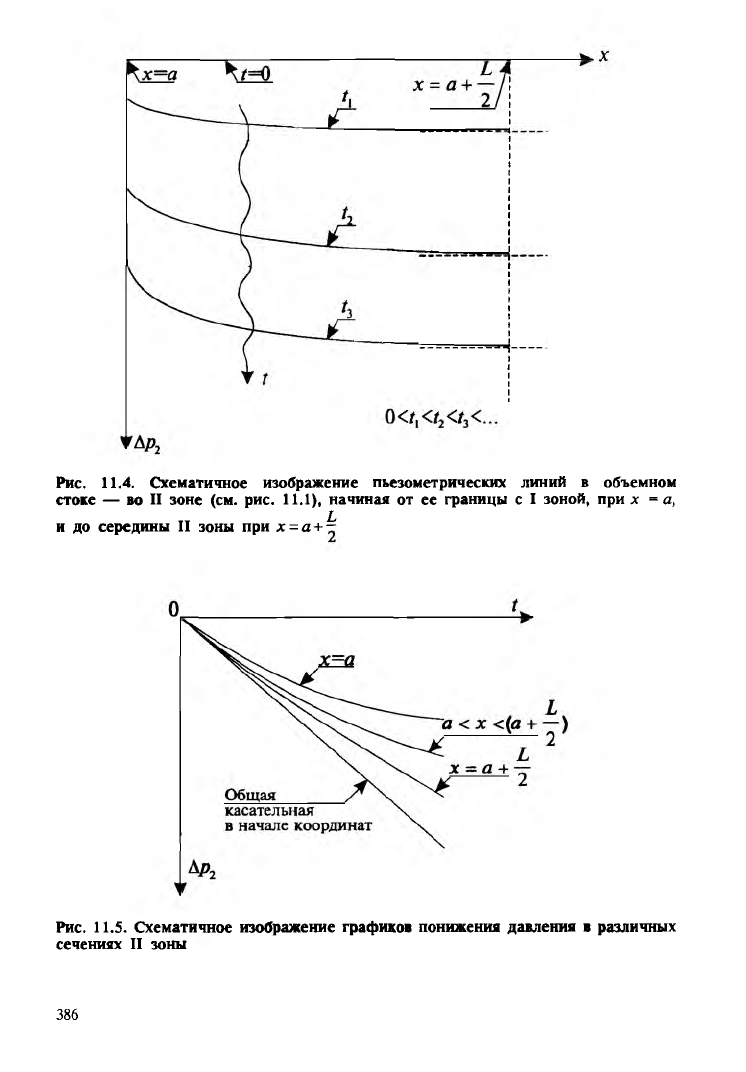
Рис. 11.4. Схематичное изображение пьезометрических линий в объемном

стоке — во II зоне (см. рис. 11.1), начиная от ее границы с I зоной, при х = а,

IT 1

и до середины II зоны при х = а + -

И здесь следует повторить то же примечание, какое было выше

сделано по поводу формулы (11.46). Именно в выведенной из нее

формуле (11.55) недопустимо одновременно принимать t = 0, х = а

или t ® 0, х ** а + Z. Поэтому равенство (11.56) можно считать

обоснованным в начальный момент для всех точек II зоны, кроме

ее границ с I и III зонами. Однако и здесь из физических

соображений можем принять, что упомянутая общая касательная

касается в начале координат (при t = 0) не только линий графиков

изменения понижений давления во всех точках внутри объемного

стока (при a<x<a+L)y но и на его границах, т.е., в частности,

при х = а.

Учитывая равенства (11.2) и (1.41), формулу (11.56) можно

переписать так:

Э Др2 С*, f)

д t

1а

а * »

(11.56а)

t - о

т.е. угловой коэффициент общей касательной в начале координат

к линиям изменения понижений давления оказывается прямо про

порциональным дебиту q с объемного стока, отнесенному к единице

его объема, и обратно пропорциональным коэффициенту упругоем

ко сти пласта р

Определим расход жидкости Q 2 (х, t) в любой момент времени

в любом сечении II зоны, учитывая равенство (11.51):

^ , j\ к _дАр2 Qc'ttif. г х-а . r a + L-x\ n i

e2(x’f) = H a “ ^ r = ~ ^ p c^ - terfc“ W ; (1L5)

Из равенства (11.57) следует, что в полном соответствии с

условием задачи в начальный момент t - 0 имеем Q (xt 0) = 0.

Полагая в этом равенстве t = °° и раскрывая неопределенность,

получаем:

. (Ч-58»

причем

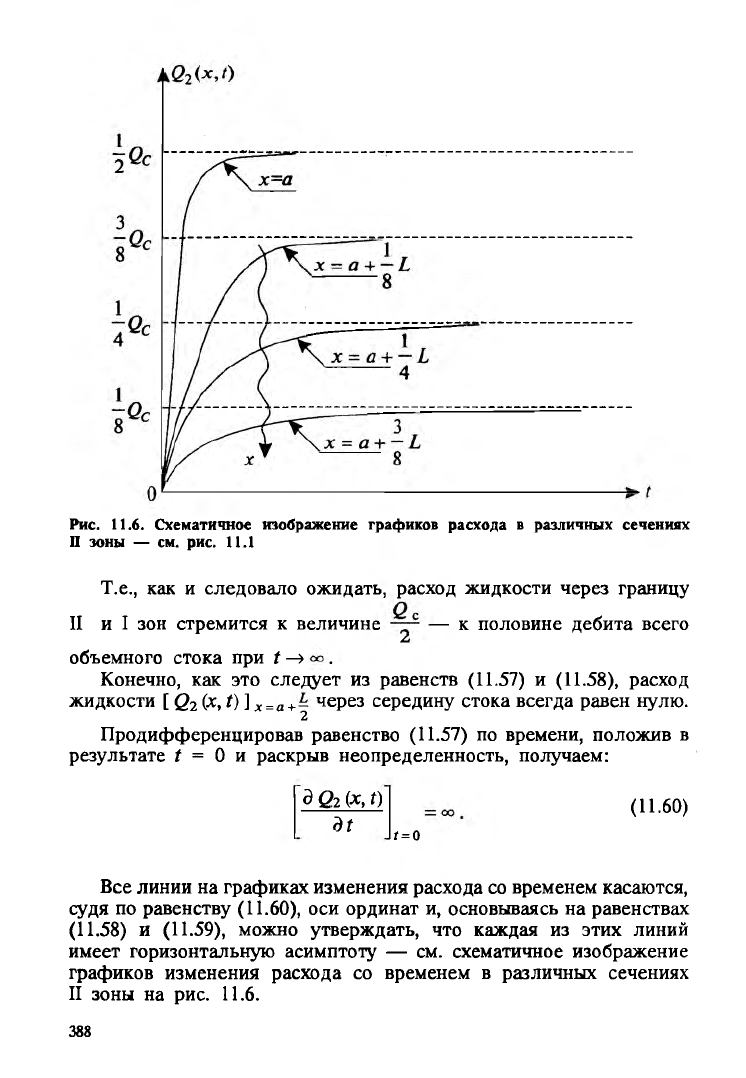
Рис. 11.6. Схематичное изображение графиков расхода в различных сечениях

II зоны — см. рис. 11.1

Т.е., как и следовало ожидать, расход жидкости через границу

II и I зон стремится к величине — к половине дебита всего

объемного стока при t —> .

Конечно, как это следует из равенств (11.57) и (11.58), расход

жидкости [ Q2 (х , t) ] х = а+- через середину стока всегда равен нулю.

Продифференцировав равенство (11.57) по времени, положив в

результате t = 0 и раскрыв неопределенность, получаем:

д £>2 (X, t)

(11.60)

Jf = 0

Все линии на графиках изменения расхода со временем касаются,

судя по равенству (11.60), оси ординат и, основываясь на равенствах

(11.58) и (11.59), можно утверждать, что каждая из этих линий

имеет горизонтальную асимптоту — см. схематичное изображение

графиков изменения расхода со временем в различных сечениях

II зоны на рис. 11.6.

Продифференцируем по х равенство (11.57):

э Qi (х, t) Qc

дх 2L

Следовательно,

э Qi (•X, t)

'Х -а ^ a + L - x 4

сг,сш +Ыс^ г

Эх

х-а

t* О

1 + erfc

2Vid

(11.62)

Из равенств (11.61) и (11.62) при любом значении х получаем:

д Qi (X, t)

Эх

At = °о

Ос

Z, 1

(11.63)

кроме того, из равенств (11.61) и (11.62) следует:

Гэ Q2 (х, t)

э 02 (*, t)

Эх

х-а

Эх

х = а+—

(11.64)

причем абсолютные величины градиентов расхода на границе II и I

зон (при х = а) с течением времени убывают.

Учитывая выводы, полученные из равенств и соотношений

(11.57)—(11.64), на рис. 11.7 схематично изображены графики

изменения расхода вдоль всех сечений II зоны (т.е. зависимости

расхода Qi от координаты х) в различные моменты

* = hi hi h • • • * ~ 00 •

Перейдем к анализу процесса перераспределения давления и

изменения величин расхода в I зоне вне объемного стока, т.е. при

-оо<х<а

— см. рис. 11.1. Для простоты опять будем рассматривать

только случай постоянного дебита объемного стока, принимая п = О

в формуле (11.32).

Полагая в формуле t= °о и раскрывая неопределенность по

правилу Лопиталя, получим, что

т.е. с течением времени понижение давления во всех точках I зоны

неограниченно увеличивается. По поводу этого результата следует

вновь, как и по поводу равенства (11.50), сослаться на оговорку, сде

ланную в § 2 главы 3.

Продифференцировав по координате х равенство (11.32), получим:

Э Aрх Qc |иУиГ

дх оЫс

. , а-х . „ а +Ь-х

tfif- ~2йГ~

(П.66)

При х = а из формулы (11.66) получим в правой части тот же

результат, что и в равенстве (11.53), т.е., как и следовало ожидать

по условию задачи, величины градиентов понижений давления

Др! и Лр2 на границе I и II зон оказались одинаковы.

На основании формулы (11.32) и с учетом равенств (11.65) и (11.66)

на рис. 11.8 схематично изображены пьезометрические линии для

различных моментов в I зоне. Для одинаковых моментов линии на рис.

11.4 должны быть продолжением линий, изображенных на рис. 11.8

Сравнивая рисунки (11.8) и (4.4), легко заметить следующее

существенное различие между ними: на рис. 4.4 все пьезометри

ческие линии имели во все моменты одинаковые углы наклона

касательных при х = 0, т.е. для всех точек плоского поверхностного

стока. Можно было убедиться в том, дифференцируя равенство

(4.13) по ^ и принимая затем ^ = 0, что угловые коэффициенты

всех касательных в начале координат по абсолютной величине

одинаковы и равны -— Равенство градиентов давления во всех

Zi о к

точках плоского поверхностного стока объяснялось постоянством

его дебита. Для рассматриваемого здесь объемного стока, пущен

ного с постоянным дебитом, угловой коэффициент касательной

для любой точки на его плоской границе при х = а (на границе

I и II зон) не постоянен, а непрерывно увеличивается, стремясь к

величине 5 ^ при t—>«. Как наглядно изображено на рис. 11.6,

2 о /с

расход жидкости через плоскую границу объемного стока с

постоянным дебитом не постоянен, а растет, стремясь к величине

— при оо.

Если продифференцировать равенство (11.32) по времени, то

можно убедиться в том, что

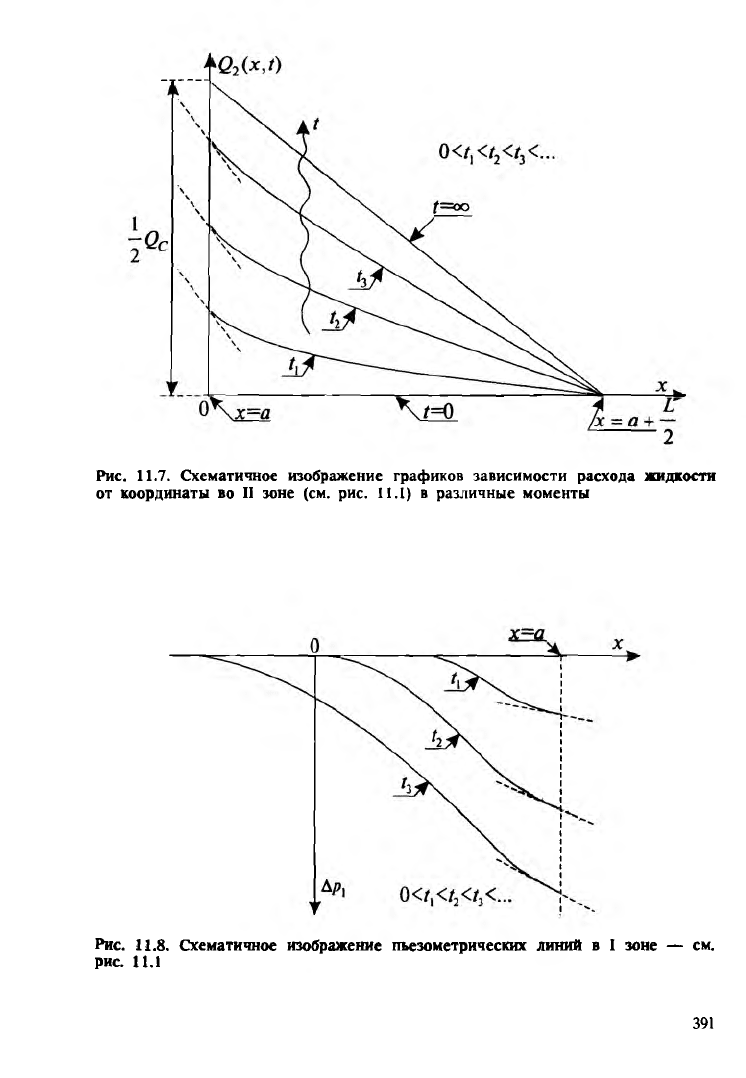
Рис. 11.7. Схематичное изображение графиков зависимости расхода жидкости

от координаты во II зоне (см. рис. 11.1) в различные моменты