Schlechta K. Nonmonotonic Logics: Basic Concepts, Results, and Techniques
Подождите немного. Документ загружается.


6.1. INHERITANCE DIAGRAMS 167
Diagram 6.2
/
S
/
P
(This is the famous Nixon Diamond. Neither potential path will be valid.
The following Diagram 6.2 may be seen as the fundamental diagram of preclusion.
It is basic to all that follows.
(Of course, there is an analogous one for the opposite polarity.)
It is essential, that the arrow r 74 s is a direct link, so it is in a way stronger
than compound paths. The path from r
to
q (read r C ... C q!), however, tells
us, that the information coming from r is more specific (and thus considered
more reliable), so the negative path from p to s via r will win over the positive
one via q. The precise inductive definition will be given below. This concept is
evidently independent of the lenght of the paths, p... ~ r may be much longer
than p-.- ~ q, so this is not shortest path reasoning (which has some nasty
drawbacks, discussed e.g. in [HTT87]).
Outline We first define potential paths (simply called paths in [HTT87], but
we would like to unify notation), tn the central part, we define valid paths, i.e.
the relation ~ for nonmonotonic inheritance. Next, we discuss properties of ~ .
Finally, we give a PMPM-algorithm, equivalent to ~ . It will be partly parallel,
partly serial, and is thus called hybrid. (We will, however, indicate, how to make
it totally parallel, there are two possibilities, one already indicated in [HTT87].)

168
CHAPTER 6. STRUCTURED REASONING
Definition of ~ (i.e. of valid paths)
Definition 6.18 a) Potential paths:
If x ~ p E F, then x -+ p is a positive potential path (pp.).
If x 74 p E F, then x 74 p is a negative pp.
If x.. 9 --+ p is a positive pp., and p -+ q E F, then x ... -+ p --~ q is a positive pp.
If z.-. -+ p is a positive pp., and p 7 c, q E ]7', then z... -+ p 74 q is a negative
pp.
There is an important difference to the monotonic case: sequences Iike x 74 p ~-- q
are no potential paths.
b) Degree
As already indicated, we shall define paths inductively. As we do not admit circles
in our systems, the arrows define a well-founded relation on the vertices. Instead
of using this relation for the induction, we shall first define the auxiliary notion of
degree, and do induction on the degree. We need a mapping f from the vertices
to natural numbers such that p --+ q or p 74 q E 17' implies
f(p)
< f(q), and define
(relative to x):
1) a generalized path is any monotone coherent sequence of arrows of any type,
beginning at x, like z -+ p 74 q 74 r --+ s etc.
2) Let o" be a generalized path ending in y, then
degp(cr)
:=
degr(y)
:= the
maximal length of any generalized path parallel to c~, i.e. beginning in z and
ending in y.
c) Inductive definition of P ~
Let cr be a potential path.
Case I: cr is a direct link E P. Then F ~ a (Garbage In)
Case II: o" is a compound potential path, degr(cr) = n, and P ~ r is defined for
all r with degree less than n.
Case II.l: Let cr be a positive pp. x..- -+ 'a --~ y. Then I' ~ cr iff
(a) P ~ x .... -~ u (The initial segment must be a path - decided by induction
hypothesis.
Warning:
It is not true, that the end-segment of a path must be a
path too - see the lack of generic stability.),
(b) u --+ y E P (Induction proceeds step by step),
(c) u 74 y ~
r
(Contradiction),
(d) For all v such that v 74 y E r and F ~ z.-. --+ v (i.e. all potentially
conflicting paths) there is z such that z --+ y E P and either z = x (the potentially
conflicting pp. is itself precluded by a direct link) or r ~ z 9 9 9 --~ z. - 9 --~ v (thus,
z is more specific than v with respect to x).
Diagram 6.3 shows the most complicated situation.
Case II.2: The negative case (it is entirely symmetrical). Let ~ be a negative pp.
x-.. -+ u ~ y, Then F ~ ~ iff
(a) r x...
-,
(b) 74 y F,
Cr,
(d) For all v such that v -+ y E F and P ~ z.-- ~ v (i.e. all potentially
conflicting paths) there is z such that z 74 y E P and either z = z or F ~ x..- --,
z... -+ v (thus, z is more specific than v with respect to x).

6.I. INHERITANCE DIAGRAMS 169
Diagram 6.3
y
V ~ .......... Z
/
"%.
"'-.. "
Finally, define F ~
xy
iff there is ,J x --* y such that F ~ or, likewise for x~.
Remark: The V- 3-quantifiers justify a game-theoretic approach to preclusion.
Consider Case II.1. Let A play negative pps, B more specific positive pps. Then
condition (d) holds iff B has a winning strategy. This part - checking possible
preclusion - will be the serial part of the algorithm.
Properties of
1) Nonmonotonieity p--,q-~r ~p--+q~r',butp~q--,r, p74r
p--~q-~r.
2) Soundness
Theorem 6.19 If F ~
xy
and F ~ x~, then x --~ y and x 74 y C P. Shortly:
Garbage Out = Garbage In. The proof goes by examination of cases.
We remind the reader that the situation in the monotonic case is different, cor-
responding to the different intuition.
3) Stability
Definition 6.20 ~ is stable iff P ~- A implies (F ~ B iff I', AI ~ B)- where Al is
the arrow corresponding to A. (This property is usually known as Cumulativity.)
Lemma 6.21 ~ defined as above is only partly stable.

170
CHAPTER 6. STRUCTURED REASONING
We have to distinguish the atomic and the generic case. ~ so defined is stable tbr
the atomic case, but not for the generic case. The result can be slightly extended
by substituting ~qnitial node" for %bject node", where z is an initial node in F,
iff there is no arrow in F, leading into z.
Theorem 6.22 If A is atomic, then P ~ A implies (F ~ B iff P, A1 ~ B). (Here
again, AI is the arrow corresponding to A.)
In the proof, the fact that A =
ap
is atomic, i.e. a can't be the destination of an
arrow is repeatedly used to show that generic arrows in F, A/must already be in
P, see the fundamental diagram for preclusion, Diagram 6.2.
It is exactly here - and in similar cases - where generic stability fails:
Theorem 6.23 Generic Stability fails in general, i.e. there is P and a generic
statement
pq,
such that F ~
pq,
but P and P,p --~ q are not equivalent with
respect to ~.
Proof Consider the following diagram F := {a -+ p, p -+ q, q ~ r, r -+ s,
p 74 r}, with the interpretation
air - breathers = s, land - dwellers = r,
mammals = q, Whale = p, Moby = a.
We haveF ~
qs,
but we cannot conclude
r' ~ as,
as P g= at.
Consider now FI := I',q --+ s: Here, Pl ~ a --~ p --+ q, q --+ s E P/, q 7# s r I7'/,
and there is no direct negative arrow a 74 s. So, all prerequisites of Case II.1 are
satisfied, and P! D a... + s, a... -+ s ~
as,
so Pl D
as.
Remark: This lack of stability precludes any m{nimal model semantics (see Sec-
tion 6.1.2.6).
4) Intersections of credulous extensions It is not true, that F ~ ~ iff ~r
is in every credulous extension, i.e. deducible from a maximal consistent subset
of P. This can be seen in the diagram {p -+ q, p 74 q}. (For a more detailed
discussion, see Sections 6.1.3 and 6.1.6.)
5) Decoupling It is not true that z has at most the properties its immediate
successors have, i.e. there is P such that F ~
zP
and for all q such that z --~ q E P
P ~qp.
Consequently, end-segments of paths are not necessarily paths.
Consider the following- diagram +.'or a counterexample:
Here, a ~ r destroys the potential path a ~ p --~ r 7g+ s, as it destroys a --+ p -~ r,
thus F ~
as.

6.1. INHERITANCE DIAGRAMS
17i
Diagram 6.4
a --
. p
8
r
A PMPM-algorithm We discuss only the main part of the algorithm, which
marks y with T, iff P ~
xy,
and with F, iff F ~ z~.
Main procedure query:
begin
loop
select-next-degree
(this procedure marks (inductively with every cali) the vertices
under current examination)
link - type[--+], on - tail[Mx], on - head[Mg~gJ --~ set - head[MT]
(direct links are valid)
link - type[~], on - tail[M=], on - head[Md~g] --+ set - head[ME]
link - type[--+], on - tail[MT], on - head[Ma~g],
off - head[MT
and
MF] --+ set -- head[MuJ
(there is tentative evidence for T: The tail-vertix has T,
thus there is a valid positive path from x to tail, by induction
hypothesis, the degree is ok, and there is no direct link
contradicting (so far, we have done only direct links))
link - type[~], on - tailfMr], on - head[Md~g],
off - head[Mr
and MF] ~
set - head[Mf]J
on[Met], of f[MIs ] ~ set[~/IT]
(no conflicting evidence)
on[Mfl ], of f[Mtt] -~ set[MF]
for c in < on[M. and MH and M~,] > do
check-preclusion(c)
(handle conflicting information)
endloop
end (of procedure)
and

172
CHAPTER 6. STRUCTURED REASONING
procedure check-preclusion(c)
begin
name[c] --* set[~/ie], eIear[Mu
and MSS ]
(tt
and ff are known)
link - type[--*
or 74],
on - tail[MT], on -- head[Mc] ~ set - tail[Mair]
(examine only direct predecessors of y = c, which are marked T, i.e.,
which have a valid positive path from z, by induction hypothesis)
loop
link - type[--*], on - tail[Mdi~
or Mp~],
on - head[MT],
off - head[Mp,.~
and
MF] ~ set - head[Mp~]
endloop
(This loop looks for the most specific information. A vertix is
marked MpT~, it is precluded, if there is a suitable more specific
one. Compare to Case II.l.(d).)
link - type[--~], on - tail[Mdi~], off - taiI[Mp~] --~ set - head[Mtt]
(direct predecessors, which are not precluded cause the tentative
conclusion tt).
link - type[~], on - tail[Meir], off - tail[Mp~] ~ set - head[Mjj]
on[M~], on[M~,], of f[MH] --* set[MT]
(no
conflicts)
on[Me], on[MH], of f[Mtt] ~ set[MF]
on[Me], on[Mtt
and MSS ] -~
set[Ms~-]
(conflict, no solution, potential paths neutralize each other)
end.
Remark:
We check all such c, one after the other, and this is the serial part of the hybrid
algorithm. It is, however, evident how to make the algorithm totally parallel:
-
either by an inflation of markers, like
dire
for all such c, and processing all those
different markers in parallel,
- or, by making a copy of the relevant subnet for all such c, and processing those
copies simultaneously.
Monotonic and nonmonotonic inheritance combined [HT88]
(The reader interested only in the main ideas may skip this Section. The defini-
tions and results presented here will not be used again.)

6.1. INHERITANCE DIAGRAMS
173
Intuition and outline Mixed Inheritance Systems contain strict inibrmation,
written p => q, and defeasible information, written p --+ q etc. For objects, only
strict information is admitted, there are no arrows a --+ p.
As the intuition is the combination of the intuitions already discussed, we can pro-
ceed directly to the definitions, define potential paths, dicuss briefly the increased
possibilities of conflicts and preclusion, and define ~ .
Potential paths
Definition 6.24 If z => p E F, then z' => p is a simple strict positive potential
path (pp.),
if x 75 p E F, then x 75 p is a simple strict negative pp.,
if z --+ p E F, then x --+ p is a simple defeasible positive pp.,
if x 74 p E F, then x 74 p is a simple defeasible negative pp.
If x..- => p is a strict positive pp., and p => q E F, then z ... => p => q is a strict
positive pp.,
if x.. :ez p is a strict positive pp., and p 7g q E F, then z .. 9 => p 75 q is a strict
negative pp.,
if x. 9 => pis a strict positive pp., and p-+ q E F, then z.-. ~ p --~ q is a
defeasible positive pp.,
if x- => p is a strict positive pp., and p 74 q E P, then z..- => p 74 q is a
defeasible negative pp.
If x. =ez p is a strict negative pp., and p r q E P, then x 9 - 9 => p r q is a strict
negative pp.
If x- --~pls adefeasiblepositivepp.,andp=>qE P, thenx'----~p=>qisa
defeasible positive pp.,
ifx. ~pls adefeasiblepositivepp., andp74-qEF, then x--.--+p75 qisa
defeasible negative pp.,
ifx. --+plsadefeasiblepositivepp.,andp+qE P, then z-..--*p--+ qis a
defeasible positive pp.,
if x-- --+ p is a defeasible positive pp., and p 74 q E I', then z--- -+ p 74 q is a
defeasible negative pp.
If x.. --+ p is a defeasible negative pp., and p <=: q E F, then z... --+ p r q is a
defeasible negative pp.
As p 75 q is equivalent with q 75 p (see [THT86]), we sometimes write p eft, q.
Negative paths have the form x-.- => p 75 q ~ ---r, x.-. ~ p 74 q r -..r,
z ... --4 p 75 q r 9 r', x. - 9 ~ p 74 q r 9 -- r, the end-segment beginning with p
will be called the negative segment.
Increased possibility of conflicts and preclusion Conflicts: In [HTT87],
conflicting paths had always start and end in common. Consider now the diagram
{r :=~ t, r...p, p...u, u 74 t}.
Here, the pp. p... ~ r conflicts with the pp.
p... ~ u S+ t, because we definitely know that all r's are t's.
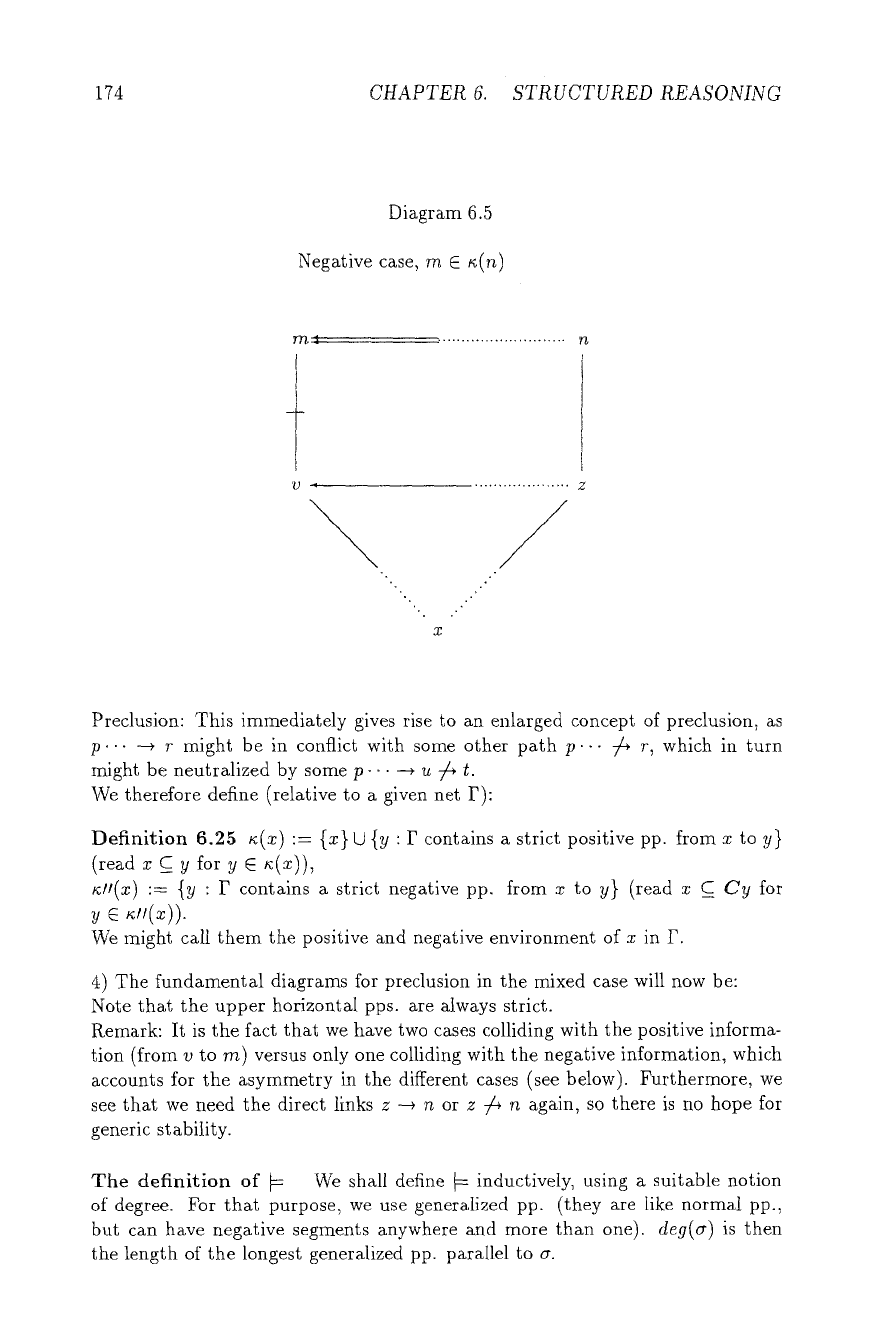
174 CHAPTER 6. STRUCTURED REASONING
Diagram 6.5
Negative case, m E n(n)
~O
"".
........................... n
.................... Z
X
Preclusion: This iInmediately gives rise to an enlarged concept of preclusion, as
p..- --+ r might be in conflict with some other path p.-- 74 r, which in turn
might be neutralized by some p--. -+ u 74 t.
We therefore define (relative to a given net P):
Definition 6.25 n(x) := {x} U {y : F contains a strict positive pp. from x to y}
(read x c y for y
nil(z) := {y : F contains a strict negative pp. from x to y} (read x C_ Cy for
We might call them the positive and negative environment of z in F.
4) The fundamental diagrams for preclusion in the mixed case will now be:
Note that the upper horizontal pps. are always strict.
Remark: It is the fact that we have two cases colliding with the positive informa-
tion (from v to m) versus only one colliding with the negative information, which
accounts for the asymmetry in the different cases (see below). Furthermore, we
see that we need the direct links z --+ n or z ;/4 n again, so there is no hope for
generic stability.
The definition of ~ We shall define ~ inductively, using a suitable notion
of degree. For that purpose, we use generalized pp. (they are like normal pp.,
but can have negative segments anywhere and more than one). deg(a) is then
the length of the longest generalized pp. parallel to ~r.
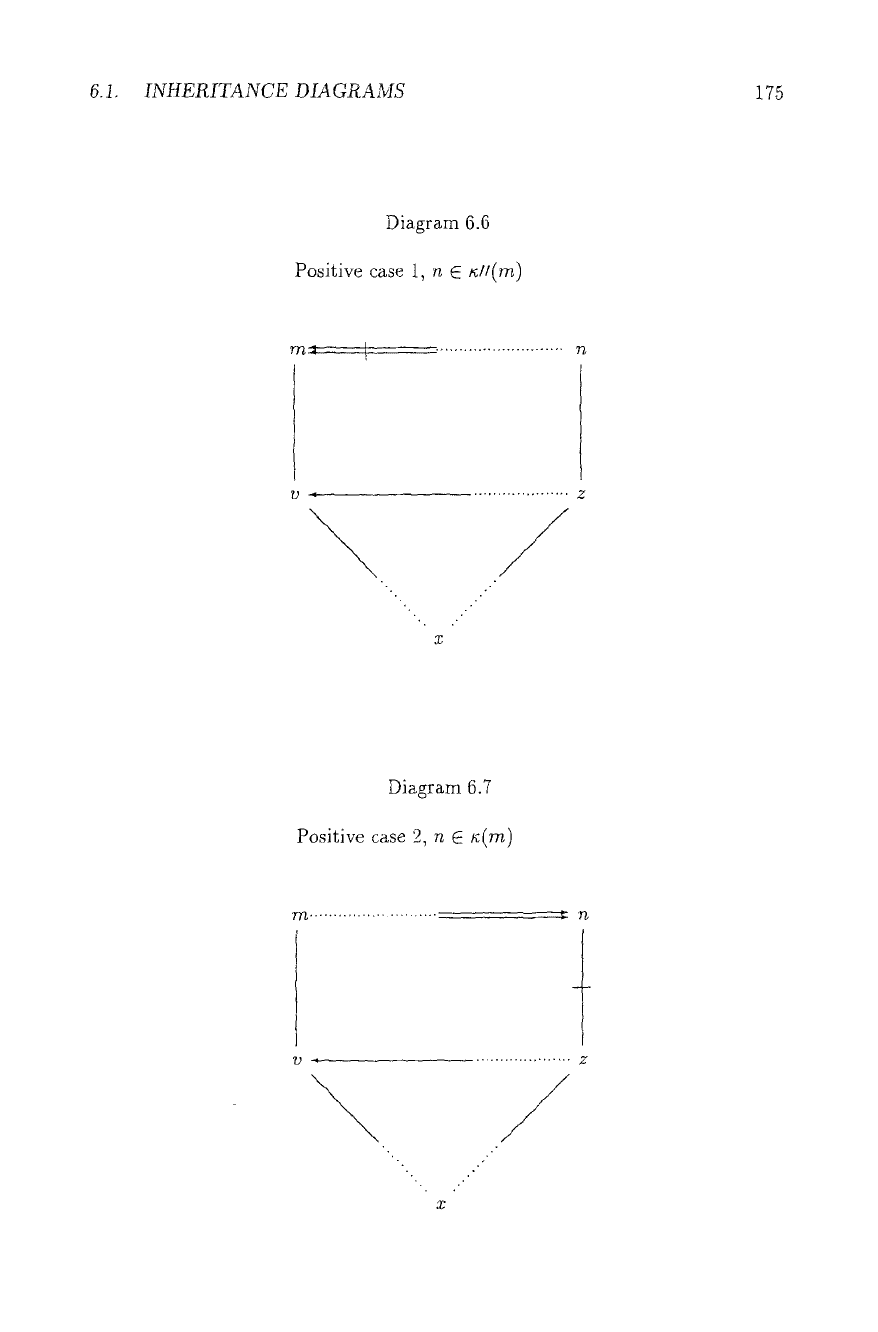
6.1. INHERITANCE DIAGRAMS
175
Diagram 6.6
Positive case 1, n E
~ll(m)
1
72 Z
">/
2C
Diagram 6.7
Positive case :2, n ~ ~(m)
r/Z ................
<
at
Z
/

176 CHAPTER 6. STRUCTURED REASONING
We write any pp. c, = 5 o #, where # is the maximal strict end segment of or.
Definition 6.26 We define F ~ or, ibr cra pp., inductively and by cases.
Case A: ~ r ~, cr r #, then P ~ ~ iff r ~ ~ and P ~ #.
Case B: cr = #, then F ~ r iff each link in o" is an element of r (the monotonic
case),
Case C-I: ~r = ~, ~r is a direct link, then F ~ c~ iff cr E F (Garbage In).
Case C-II: cr = ~, cr is a compound pp.
Case 1: cr is positive of the form z. 9 9 ~ u --~ y.
Then F ~ cr iff
(a) I' D x.'. ~ u (the initial segment is valid by induction),
(b) u + y E P (the induction proceeds one step - see discussion of stability),
(c.1) w e 74 r r A r
@.2) Vm E xH(y)(x ~ m f[ r h m f[ ~(x)) (direct links win, even if combined
with strict links),
(d.1) For all v,m such that: 17 ~ z,.- -~ v, v 74 m E I' and m E ~(y) there is
z,n such that: P ~ z...~ z... ~ v with z --* n E I2 and m E ~('n),
(d.2) For all v,m such that: F ~ r -) v, v --4 m E F and m E ntt(y) there is
z,n such that: F ~ x.-. -~ z... ~ v with either (i) z ~ n E F and m E ntt(n)
or (ii) z 74 n E F and n E n(m). (Cf. the fundamental diagrams and the remark
on asymmetry.)
Case 2: a is negative of the form x,.. ~ u ~ y.
Then r ~ cr iff
(c) Vm.y e t~(m)(x --> m r r A m ~ ~ ( ~ I) ) ,
(d) For all v,m such that: F ~ x-.. --~ v, v -~ ra E F and y E ~(m) there is z,n
such that: F ~ x.-. ~ z... ~ v with either (i) z ~ n E r and m E ~tt(n) or
(ii) § r and e
Towards logics and minimal model semantics for nonmonotonic inher-
itance
[TH89]
We discuss
a
4-valued modal propositional logic, and minimal model semantics,
i.e. a preorder semantics for the logic. Next, we do a tentative extension towards
quantification, to simulate generic statements. Finally, we show that the existence
of a minimal model semantics for inheritance would entail full stability.
The modal propositional logic
Definition 6.27
a)
Formulae: A molecular formula is an atomic formula or a
negated atomic formula. If A and B are formulae, so are -~A, A V B, A A/3. If
A is a formula, so is O A, |
b) Models: Models assign subsets of' {T, F} to formulae, written M ~T A for
T E M(A) etc. The rules for composite formulae are:
M ~T -~A iff M ~, A,
