Schlechta K. Nonmonotonic Logics: Basic Concepts, Results, and Techniques

6.1. INHERITANCE DIAGRAMS

177

M VF -,A iff M ~T A,

M~TAABiffM~TAandM~TB,

M ~F AA B iff M ~r A or M ~F B,

M ~T A V B iff M ~T A or M ~T B,

M~rAVBiffM~FAand M ~F/3,

,4J PT OA iff M ~T A,

M ~v 0 A iff M ~=T A,

M ~T | iff M ~, A,

M

~=F

| iff M ~F A.

We may thus read M ~T 0A: we have information, that A, and M ~T •A: we

have no information, that A is wrong

We define now special cases of the -<-relation between models in preferential

structures.

Definition 6.28 Let M < M/ iff for all atomic formulae

A M(A) C_ MI(A).

A normal model is a minimal one with respect to this order, it is minimal in

"information content". Define F il- A iff M ~T A for all minimal models of F. Ib

is nonmonotonic - see the example given in [TH89].

Extending the logic for .4 and 74 Remark: p -4 q is

not ~p V q,

but the

familiar "all p are normally q" of nonmonotonic inheritance.

Definition 6.29 Since the arrow is already in multiple use, define

M ~r Vx(r Cx) iff

Vd (M ~T Cd ~ M

PT

~bd) (read Vz(r ~bx): Vx(r .4 r

and define

p --4 q :=

Vx(px A Oqx,

qx), p 7/+ q :=

Vx(px A G~qx, -~qx).

Recall here the intuition: M ~T @A: we have information,

that

A, M ~:r |

we have no information, that A is wrong, M ~T O-,A: we have no information,

that A is true.

Revising minimality Leaving the definition of minimality unchanged, we get

counter-intuitive results, e.g. for the diagram

a-4p--~q.

Then F ~

qa,

but there is a minimal model of P, in which

-,qa

holds, as

|

is

not satisfied.

We now minimize in lexicographic order:

I) inconsistencies, the set of atomic formulae A, such that A and -~A are true in

M,

2) anomalies (defined below),

3) information content, the set of moIecular formulae true in M.

We thus define:

~[78 CHAPTER 6. STRUCTURED REASONING

Definition 6.30 < p --* q, d > is

an anomaly

iff

1. p ~ q E F, d E M, M ~T pd A G~qd (we have information that pd, and no

information that qd) or

2. p74 q E F, dE M, M ~T pdA Gqd.

This notion of minimality does not permit preclusion.

We conclude with the following result (not found in the discussed literature):

Minimal model semantics entails stability

Remark 6.31 Let ~ be an inheritance relation, representable by minimal model

semantics, then ~ is fully stable. (We take the liberty here of identifying arrows

with results.)

Proof Let P ~ A iff A is true in every minimal model of F. By prerequisite,

r ~ a iff F ~ A. Let F ~ A. We have to show: VB(F ~ B iff F, A ~ B). We use

a standard technique for arguing with minimal model semantics. Let re(P) be the

set of models of F, i.e. rn I~ X for all X E P. Let #(P) C m(I') the set of minimal

models of F. We show #(F) = #(F, A). As F ~, A, t*(F) C re(F, A) C_ re(F).

"D":

.(r,a).

Suppose x ~ >(P). So, t~here is y E #(P), y < z. But, as

#(F) C re(r, A), y E ,rn(P, A), so x is not minimal in re(F, A). Contradiction.

"C_": So #(F,A) C #(P) C m(F,A) C rn(P). Suppose x E >(P) - #(F,A). As

>(P) C_ m(I', A), there is y E #(I7', A) C #(P), y < x, so x is not minimal in p(P),.

Contradiction. 2~hus, #(I') = #(P, A), and P ~ B iff F, A ~ B, and P ~ B iff

P,A ~/?, c3

6.1.3 P~eview of other approaches and problems

Introduction

This Section has an overview character, discussing a wide variety of approaches in

defensible inheritance. It is held essentially self-contained. Our aim is to discuss

some basic principles underlying different approaches to defensible inheritance

and to examine problems of these approaches as they already appear in quite

simple diagrams. We build upon, but go beyond, the discussion in [THT87].

We shall limit the discussion to purely defensible finite acyclic inheritance nets,

i.e. finite acyclic graphs, with two kinds of nodes and arrows (links). As above,

the nodes stand for objects or classes of objects. To simplify matters, we assume

in our theoretical discussions to have only class-type nodes. The positive arrows

z --4 y mean as usual something like "normally, x's are y's", or "most x are y," the

negative ones x 74 y "most x are not y." We consider a net F as information from

which to draw conclusions of two kinds: First, we may say that P permits some

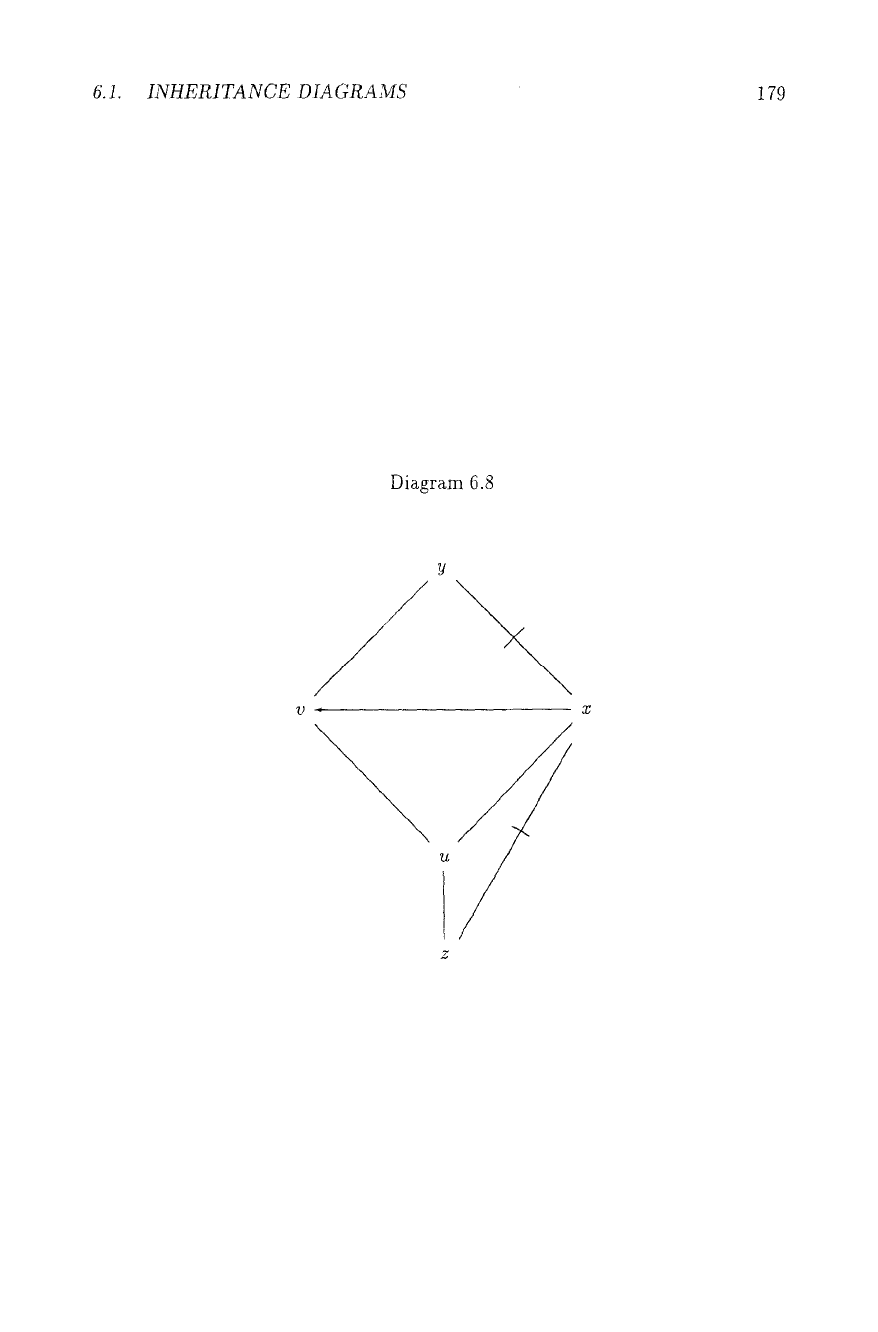
"line of reasoning", i.e. a "path" of concatenated arrows of F, like or: u --~ x 74 y

\

c~

180

CHAPTER 6. STRUCTURED REASONING

in Diagram 6.8, second, that F permits a result, like "most u are not y" here, if

this is the conclusion of a permitted line of reasoning.

Permitted paths and results will also be called "valid" or "accepted" in F, some-

times written F ~ cr etc. To differentiate from arrows, positive results will again

be noted

xy,

negative ones aT d.

We shall examine several definitions of acceptability of paths and their results

for defensible inheritance nets. In Section 6.1.3.2, we try to shed light on some

of the fundamental differences between various definitions, in Section 6.1.3.3, we

discuss problems specific to some approaches, in Section 6.1.3.4, we discuss some

horizontal and vertical coherence properties.

Fundamental differences

Extension-based versus directly skeptical definitions As this distinction

has already received detailed discussion in the literature, we shall be very brief

here. An extension of a net is essentially a maximally consistent and in some

appropriate sense reasonable subset of all its potential paths. This can of course

be presented either as a liberal conception (focussing on individual extensions) or

as a skeptical one (focussing on their intersection - or more accurately, as discussed

below, the intersection of their conclusion sets). The seminal presentation is that

of [Tou86], as refined by [San86]. The directly skeptical approach seeks to obtain a

notion of skeptically accepted path and conclusion, but without detouring through

extensions. Its classic presentation is that of [HTT87]. Even while still searching

for fully adequate definitions of either kind, we may use the former approach as

a useful "control" on the latter. For if we can find an intuitively possible and

reasonable extension supporting a conclusion xg, whilst a proposed definition for

a directly skeptical notion of legitimate inference yields xy as a conclusion, then

the counterexemplary extension seems to call into question the adequacy of the

directly skeptical construction, more readily than inversely.

i

Upward versus downward chaining The view of paths as lines of reasoning

leads naturally to inductive definitions of accepted paths: for cr : x -~ y --~ ... -+

z ~-~ u (where ~-~ stands for -~ or 74) to be valid, either the initial segment

cq : x --+ y -~ ... -~ z or the end segment ~lt : y ~ ... -+ z ~-~ u has to be

valid already. The first condition is calIed upward, the latter downward chaining,

double chaining is the conjunction of both. At first sight, a decision between

the two seems arbitrary. Yet Diagram 6.8 shows that downward chaining might

violate the principle of specificity: Reasoning upward, we will accept z -~ u --~

v --~ y, thus

zy,

because the possible preclu'sion z -~ u --+ x --+ v and z ;/* y

is itself destroyed by the still more specific information z ~ x. In downward

chaining, however, only properties of direct successors can be inherited. And in

the example, no direct successor w of z has the accepted property

wy,

as the

destruction z 74 x of z --~ 'u -* x --~ v is no longer "visible" at u. It thus seems

that in normal cases the result of upward chaining is the better one. Thus, there

is some good reason to opt for upward chaining definitions. A word of warning: A

6.1. INHERITANCE DIAGRAMS

181

superficial impression of [SL89] might be that whilst upward chaining is tractable,

downward chaining is not, thus giving an additional criterion in favour of upward

chaining. A more careful study of their results reveals that they show that whilst

finding extensions defined by upward chaining is tractable, finding extensions

defined by

double

chaining is not. Certain problems in the extensions approach

have led [Tou86] and others to consider double chaining. This will be discussed

in more detail in Section 6.1.3.4. Prom now on, all definitions considered shall be

(at least) upward chaining.

On-path versus off-path preclusion This is a rather technical distinction,

discussed in [THT87]. Briefly, a path ~r: x -4 ... ~ y -4 ... --~ z and a direct

link y 74 u is an off-path preclusion of r: x --* ... -4 z --* ... --~ u, but an

on-path preclusion only iff all nodes of r between z and z lie on the path c~. Thus,

e.g. Diagram 6.8 shows only on-path preclusion. A second warning: The wording

of the definition seems to be a little misleading. A precise definition of on-path

preclusion is given implicitely in [Tou86]: [THT87] refers to its construction as

being on-path.

Split-validity versus total-validity preclusion Consider again a preclusion

~r : u .4 ... --4 x .4 ... --~ v, and x 7z* y oft : u -4 ... ~ v --~ ... ~ y. Most

definitions demand for the preclusion to be effective - i.e. to prevent r from being

accepted - that the total path c~ is valid. Some ([GV89], [KK89], [KKW89a],

[KKW89b]) content themselves with the combinatorially simpler separate (split)

validity of the lower and upper parts of ~r: cr! : u ~ . .. --* x and o-II : x -+ ... -4 v.

In Diagram 6.9, it is easily seen that ~r : u -4 x --+ w -4 v, x ~ y is only a split

valid preclusion, as the link u ~ w destroys ~r as a whole.

Thus, split validity preclusion will give here the definite result u~. With total

validity preclusion, the diagram has essentially the form of a Nixon Diamond.

A supporting argument for total validity preclusion can be given as follows :

If we do not accept ~ as true, but only or1 and all, the truth of cql might fail

to take into account the pecularities of u, for the part of x containing u might

behave irregularly. For illustration, interpret Diagram 6.9 by assigning subsets of

the real line to objects, and (probabilistic) set-inclusion to arrows: u := [-1, 0],

x := [-10,100], w := [0, 1000], v := [-1, 100001, y := [-0.5, 0] U [100, 10000]. (A

general problem with probabilistic interpretati6ns of defensible inheritance nets

is discussed in Section 6.1.5.) Using techniques as in Diagram 6.8, one may have

valid total preclusion, but invalid split preclusion too.

Intersection of extensions versus the intersection of their conclusion

sets Going into more technical details now, we need more terminology. Let us

call all sequences of concatenated arrows of a net F, positive or negative, gener-

alized paths. Thus, valid paths are potential ones, and the latter are generalized

paths. If x, y are nodes in F, [x,y] shall denote the minimal subgraph of F

containing all generalized paths in F beginning in x and ending in y.

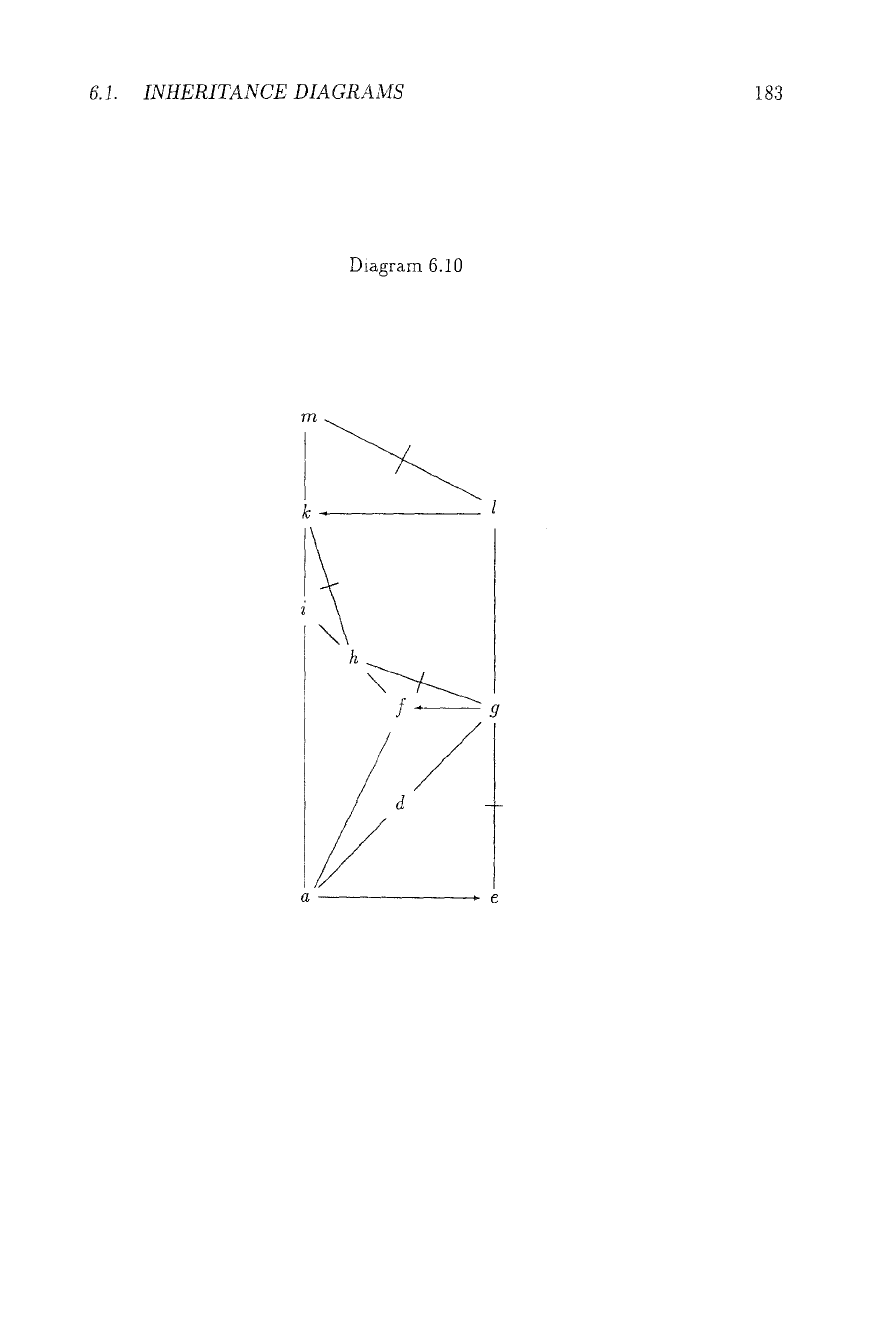
The problem is perhaps best illustrated by discussing an example, Diagram 6.10.

182

CHAPTER 6. STRUCTURED REASONING

Diagram 6.9

Y

~- W -~ X

lz

At the heart of Diagram 6.10 is a Nixon-Diamond

[a,g].

The.diagram has two

extensions. If we decide [a, 9] positively, i.e. make a --+ d --* 9 vMid, then

a --+ d -+ g -+ f and g 74 h is a valid preclusion of a --+ f --~ h, so a --~ f -+ h --* i

and h 74 k is no valid preclusion of a ~ i --+ k. But a --+ d --~ g --+ l -~+ i

together with 1 74 k is then a valid one. A negative choice in [a, g] will make

a --4 f --+ h --+ i valid (thus, with h 74 k a valid preclusion of a ~ i + /c) and

a --+ d ~ 9 -+ I --+ i invalid. The reader should note that all preclusions are on-

path: a simpler diagram with off-path preclusions can be found in Section 6.1.5,

Diagram 6.23. Thus, we have in all extensions a valid preclusion of a --+ i --+ ~:, a

valid negative path from a to k, thus a~, but ~ neither a common valid preclusion

of a --~ i ~ k, nor a common valid negative path from a to h. This diagram

teaches us a number of things.

1) One might have "floating conclusions", i.e. a conclusion might hold in all exten-

sions without a

common

valid path to support it. (A similar result can be found

in [Ste90], working with an array of Nixon Diamonds, instead of preclusions.)

2) Consequently, validity in the intersection of extensions should not be defined

by the set of common paths, but by the set of common conclusions.

3) How on earth is a directly skeptical approach supposed to "remember" which

dedsion and diamond its paths come from? Indeed, we will show in Section 6.1.5

below that any direct definition of inheritance, which has a (fixed) finite number

of truth values, and satisfies a very weak and natural but somewhat technical

condition will fail to give the same results as the intersection of extensions. The

result will be motivated and taken up again in Section 6.1.3.3. 4) It reveals

the intricate interplay between decisions (in Nixon Diamonds) and preclusion s

possible in extensions - see Section 6.1.3.3.

6.1. INHERITANCE DIAGRAMS !83

Diagram 6.10

rn

h

f~ 9

184

CHAPTER 6. STRUCTURED REASONING

Diagram 8.11

z~ y

T/ 2

2/

Problems specific to certain approaches

Discussion of the [HTT87] approach, the problem of positive support

The problem has wider repercussions, as will be seen in our discussion of con-

flictual &coupling, but we will treat it here, as it arises in a clear form in the

[HTT87] approach. Consider Diagram 6.11I := [u, y] C_Diagram 6.11.

[HTT87]'s definition will make the path u --* v -~ y valid, despite the valid

preclusion u + w + v, w 7z~ y. The conclusion

uy

itself is, of course, correct

by the validity of u -* x --* y, but the argument u ~ v -~ y seems wrong. (A

similar problems arises for Nute's system [NBD89], see also [Nut88a], [Nut88b],

[Nut89].) The distinction may seem petty, but look at the full diagram. [HTT87]

will accept the preclusion u + v --* y and v 74 z of u -~ z --* y -~ z and thus

arrive at ug, whereas the approach %orrect in argument" will see u --~ x --~ y

as the only valid path from u to y, so we have no preclusion, but only a Nixon

Diamond situation: u --~ v 74 z vs. u--, x ~ y ~ z, so no conclusion in the

skeptical definition. Of course, there is an easy way out: Accept as valid only

paths, that are not precluded by valid paths.

When analysing the situation, it helps the intuition to take the wider view of

argument systems: A nonsensical argument c~ does not become acceptable be-

cause its conclusion coincides with the conclusion of a sound argument 7- Thus,

in the above diagram, there is no reason to see in the valid (and best) argument

6.!. INHERITANCE DIAGRAMS

185

Diagram 6.12

f

d

q C

a

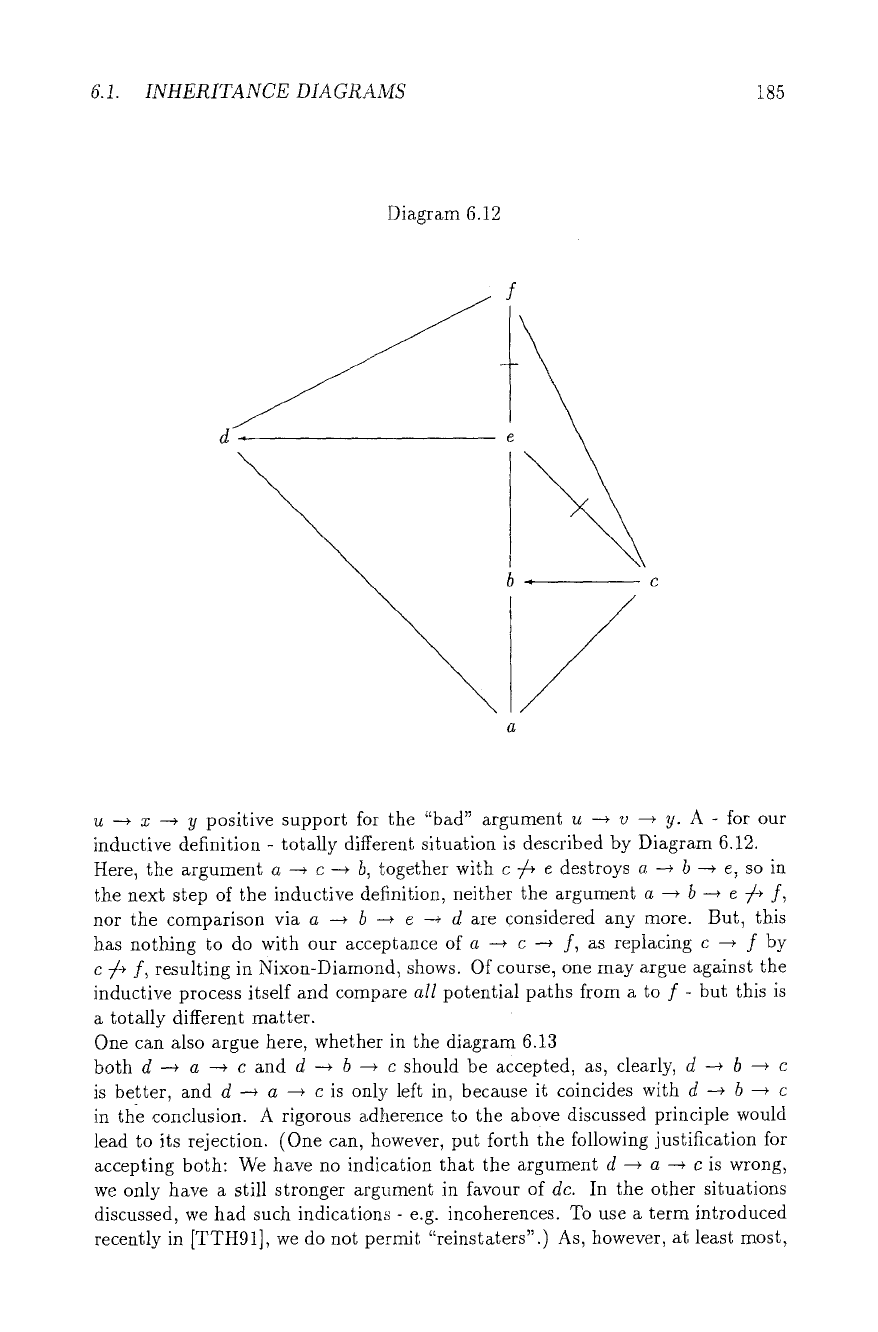
u --+ z --+ 9 positive support for the "bad" argument u --~ v --+ y. A - for our

inductive definition - totally different situation is described by Diagram 6.12.

Here, the argument a --* c -+ b, together with c ~ e destroys a ~ b --* e, so in

the next step of the inductive definition, neither the argument a --~ b --+ e 7~ f,

nor the comparison via a ---+ b --~ e --4 d are considered any more. But, this

has nothing to do with our acceptance of a --~ c --~ f, as replacing c -+ f by

c 74 f, resulting in Nixon-Diamond, shows. Of course, one may argue against the

inductive process itself and compare

all

potential paths from a to f - but this is

a totally different matter.

One can also argue here, whether in the diagram 6.13

both d --+ a --+ c and d + b + c should be accepted, as, clearly, d --+ b --+ c

is better, and d --~ a ~ c is only left in, because it coincides with d -+ b --* c

in the conclusion. A rigorous adherence to the above discussed principle would

lead to its rejection. (One can, however, put forth the following justification for

accepting both: We have no indication that the argument d --+ a --+ c is wrong,

we only have a still stronger argument in favour of

dc.

In the other situations

discussed, we had such indications - e.g. incoherences. To use a term introduced

recently in [TTH91], we do not permit "reinstaters".) As, however, at least most,

186

CHAPTER 6. STRUCTURED REASONING

Diagram 6.13

C

a .4

d

defeasible inheritance formalisms accept both, we shall not leave main street here.

Another interesting problem shows up in the "Double Diamond" Diagram 6.141 :=

[a,j] C

Diagram 6.14, see also Diagram 6.22.

As pointed out already in [HTT87], their definition gives a wrong result: By

skepticism, there is no path from a to i, so, by upwards chaining, the potential

path a + f -+ g -+ j is unchallenged. On the other hand, there is a genuine

possibility for aT, by the path a -+ f ~ i 74 j, which shows up in one ex-

tension. (Again, the same problem can be found in [NBD89].) Thus, by being

skeptical in the small diagram [a, i], we end up credulous in Is, j] with respect to

a j,

as we suddenly believe in one choice, when the opposite is (almost) as good.

This phenomenon, as well as the one in the full diagram Diagram 6.11, may be

seen as special cases of the following general phenomenon:

Usually,

inheritance

constructions are rich enough to turn

any

difference between two definitions of

validity ~ and ~ t either way round, so there is no proper inclusion in the sense

that F ~ (r implies P ~ ~a but not vice versa. Of course, examples like ~ :=

provide exceptions, but the statement is correct in most interesting cases. What

can we do? First, one might try to work with ~an alternation of credulous and

skeptical standards: If we want to be skeptical with respect to

aj,

we have to

be credulous with respect to

ai,

and somehow admit the possibility a --+ f --+ i.

Apart from technical difficulties, which can be guessed in the full diagram Dia-

gram 6.14, where we would have to start skeptically in [a, l], and liberally in [a, i]

to arrive at skepticism with respect to

ap,

this involves an element of "cheating":

We have to look upward to the result we would like to have, at least counting

the number of alternations of standards, and cannot proceed purely inductively

Schlechta K. Nonmonotonic Logics: Basic Concepts, Results, and Techniques

Подождите немного. Документ загружается.