Schlechta K. Nonmonotonic Logics: Basic Concepts, Results, and Techniques
Подождите немного. Документ загружается.


6.1. INHERITANCE DIAGRAMS
187
Diagram 6.14
P
.I h j--* i*j
k~a .f .g
any more. As a second possible solution, one may preserve the destructive capa-
bilities of invalid paths up the inductive hierarchy, thus essentially introducing a
third truth value (valid, invalid, invalid but still destructive - because ruled out
only by contradiction, not preclusion). Indeed, there are solutions of the Double
Diamond problem still in the spirit of a directly skeptical approach, which fol-
low this strategy, either explicitely [Sch89-1], or implicitely [GV89]. These will,
however, fail to give intuitive results in other'diagrams - measured by the exis-
tence of reasonable extensions. As mentioned already, this failure has a deeper
reason: under some weak assumpt, ions, we can show that in principle no direct
skeptical definition with finitely many truth values can match exactly the intersec-
tion of extensions. Moreover, complexity results ([SL89] for on-path preclusion,
[S&89-1] for off-path, and slightly modified, for on-path preclusion) tell us that
finding the intersection of extensions is NP-hard. Our argument is as follows: We
code propositional logic into nets, by representing each propositional variable by
a Nixon-Diamond, handling negation by preclusion, and disjunction by joining at
top and bottom.
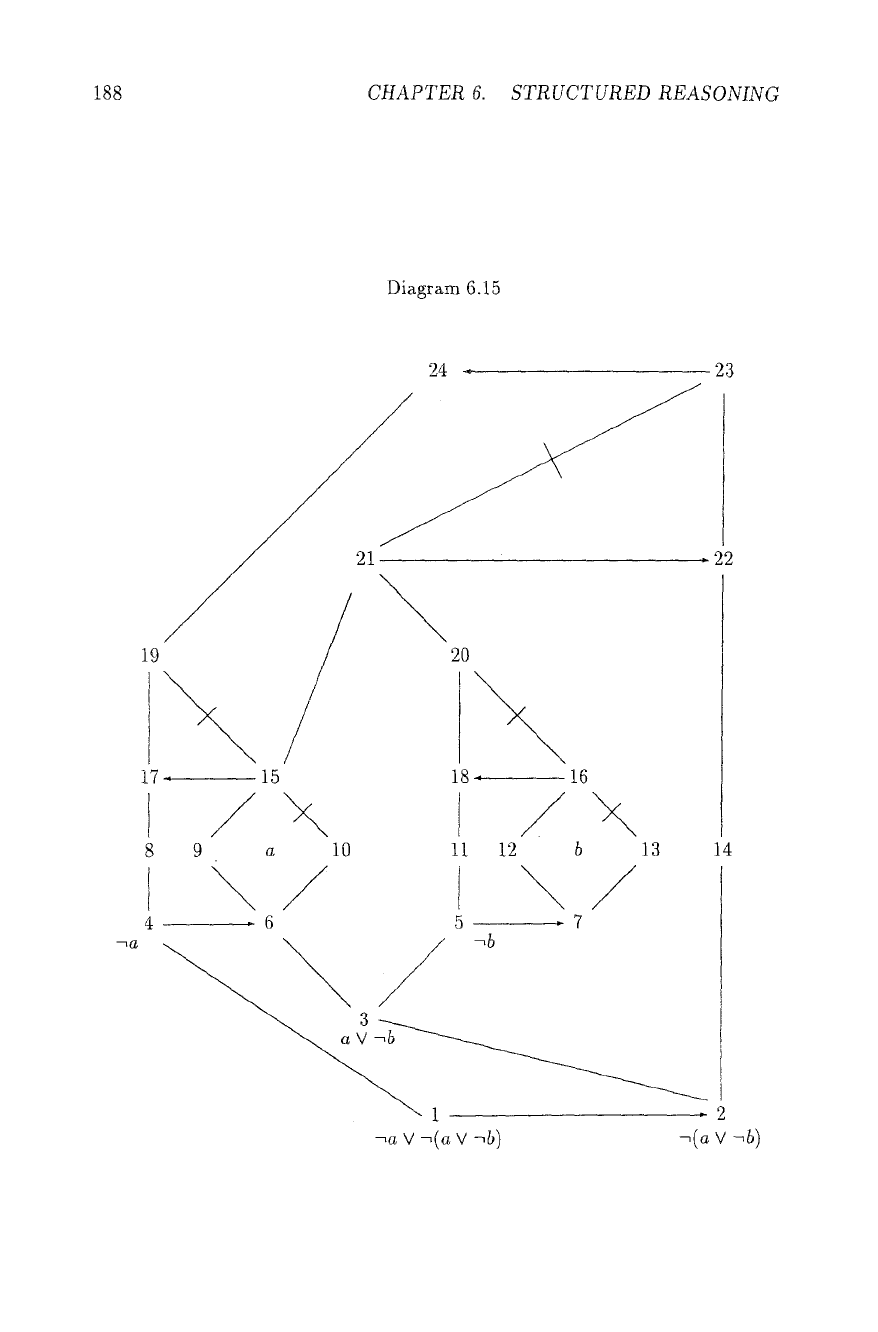
As an exercise, we encode =a V ~(a V -~b), Diagram 6.15 (the formula is true iff
a is false).
If a is true, we have preclusion of the left hand positive path, i.e. 1-4-8~17-19-24.
As there can be no negative path from 1 via 5 to 21, there is no contradiction
to 1-4-6-9-15-21-22, and the right positive path from 1 to 24 is precluded too. If
a is false, there is nothing to prevent the left hand positive path. So we have a
(positive) path from bottom to top iff the formula is true.
Corollary 6.32 Deciding the intersection of extensions of nets is NP-hard.
Discussion of Stein's approach This approach can be very roughly de-
scribed as follows (see [Steg0], [SteSg]): First, credulous extensions of F are de-
188
CHAPTER 6. STRUCTURED REASONING
Diagram 6.15
-la
24 -,
23
.22
19
17.,
15 18,
--16
/\ /\
8 9 a 10 11 12 b
,
\/ \/
4 6 5-- -7
~a V -~(~ V -~b)
13 14
2
-~(a v <,)

6.1. INHERITANCE DIAGRAMS
t89
fined - call them L-extensions, as they differ from all extensions we have consid-
ered: So far, specificity is left totally out of consideration. (Thus, e.g. Diagram
6.8 will have an L-extension containing u ~ v 4.4 y.) In a second step, a re-
lation of preference is defined between L-extensions. Third, the intersection of
preferred L-extensions is taken. A tractable algorithm is given, though without
proof of equivalence to the definition. The decisive step is, of course, the second
one. An L-extension X is said to be preferred over Y, iff Y supports a precluded
path, which is not redundant, and not supported by X. The notion of preclusion
used by Stein is (prima facie) a very simple one, much stricter than even on-path
preclusion. The interesting condition is "redundancy". A redundant path con-
tains redundant links, which are shortcuts of longer paths, to which there is no
opposite alternative of equal strength. And here lies the crux of the matter! In
Diagram 6.10 e.g., a ~ f would be redundant in the absence of a ~ e 74 g. The
mere negative
possibility a --* e 74 g
however makes a --* f non-redundant. The
end-result is that in Diagram 6.10, the preference relation between L-extensions
is empty, so that we still have no conclusion for
akin-k,
contradicting the "true"
intersection of extensions. In a very rough summary, this approach first takes a
superficial look at Nixon Diamonds, considers only the negative possibility, looks
then at preclusions, and reconsiders (preferred) extensions again in the end. For
details, we have to refer the reader to the original articles.
The extensions approach - coherence properties
In Section 6.1.3.2, we have described extensions as reasonable maximal consistent
subsets of the potential paths - where "reasonable" stood for taking specificity
into account. There is a property subtler than consistency and specificity, which
we might call coherence.
Before discussing the question, we recall the - rough - principles of (upward)
reasoning:
t. Proceed inductively, by reasons, not by consequences.
2. If c~ is better than r, and they contradict each other, reject r.
3. In case of contradictions between ~r, r of the same quality:
- in the sceptical approach: accept neither,
- in the extensions approach: branch into different extensions.
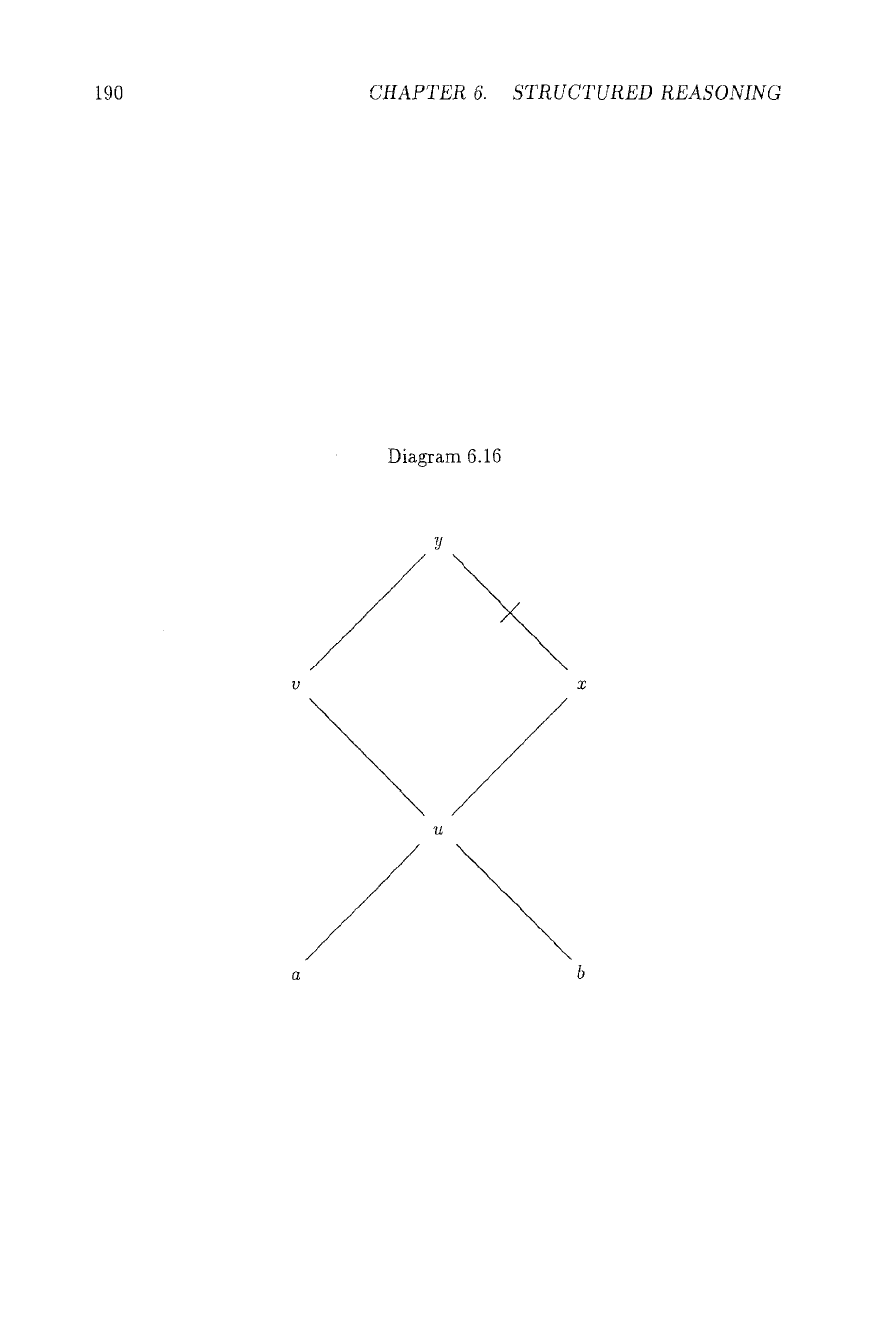
Look now at Diagram 6.16.
In upwards chaining definitions, there is nothing so far to prevent extensions
containing a --~ u --~ v --4 y, and b + u + x 74 y, a phenomenon, called
"capriciousness" by Thomason, we may call it horizontal incoherence. Here, we
are mainly concerned with a more disturbing situation, vertical incoherence or
"decoupling" (see [Tou86]): Consider
[a,y] C
Diagram 6.16. We might have a
"strange" extension with a ~ u --~ v --* y and u --* x 74 y as valid paths. A
solution to both problems would be double chaining. Yet, as we have seen, this
has undesirable consequences too, it is too radical a remedy. (The neglect of
specificity in downwards chaining, discussed in Section 6.1.3.2, applies a tbrtiori
to double chaining). Looking back at Diagram 6.8, we see that we had there a
C~
Y
Y
j/
O~
h~
c~
c~

6.1. INHERITANCE DIAGRAMS
191
Diagram 6.17
[ • \
f g" h
\ / \ /
b c
a
r
f
/c n
\
X \
l ~ rn
/ \ /
d e
a
Identify both a's and both o's
good reason (the preclusion z 74 z) to conclude
zy
and u~, whereas in the present
case, the decoupling is capricious or "unforced".
We consider such incoherences as counterarguments, though not as strong as
outright contradictions. This leads us in a natural way to evaluate potential paths
in quality as precluded < contradicted+incoherent < contradicted < incoherent.
(We need not go below precluded, as such paths are "out" anyway.)
Thus, assuming - in a suitable inductive definition - that u ~ v -+ y is already in
an extension E of Diagram 6.16, a -+ u --+ v --+ y and a --+ u --+ z 7[+ y contradict
each other, but, in addition, a -+ u --+ z 74 y is incoherent with u ~ v --+ y, so
it is less acceptable, and a --~ u --+ v --+ y is the best choice, and thus accepted
- there will be only one continuation of the extension E. Likewise for the full
Diagram 6.16, where only a --+ u -+ v --+ y and al --+ u -+ v --+ y will be the best
possibilities.
In contrast, reconsidering Diagram 6.8, we see u --~ z 74 y has to be accepted,
and z ~ u + v --+ y is the best alternative, though incoherent with u ~ z 74 y.
Our simple evaluation schema permits us to solve such somewhat complicated
diagrams as Diagram 6.17 and Diagram 6.18 in an at least not outright unrea-
sonable way:
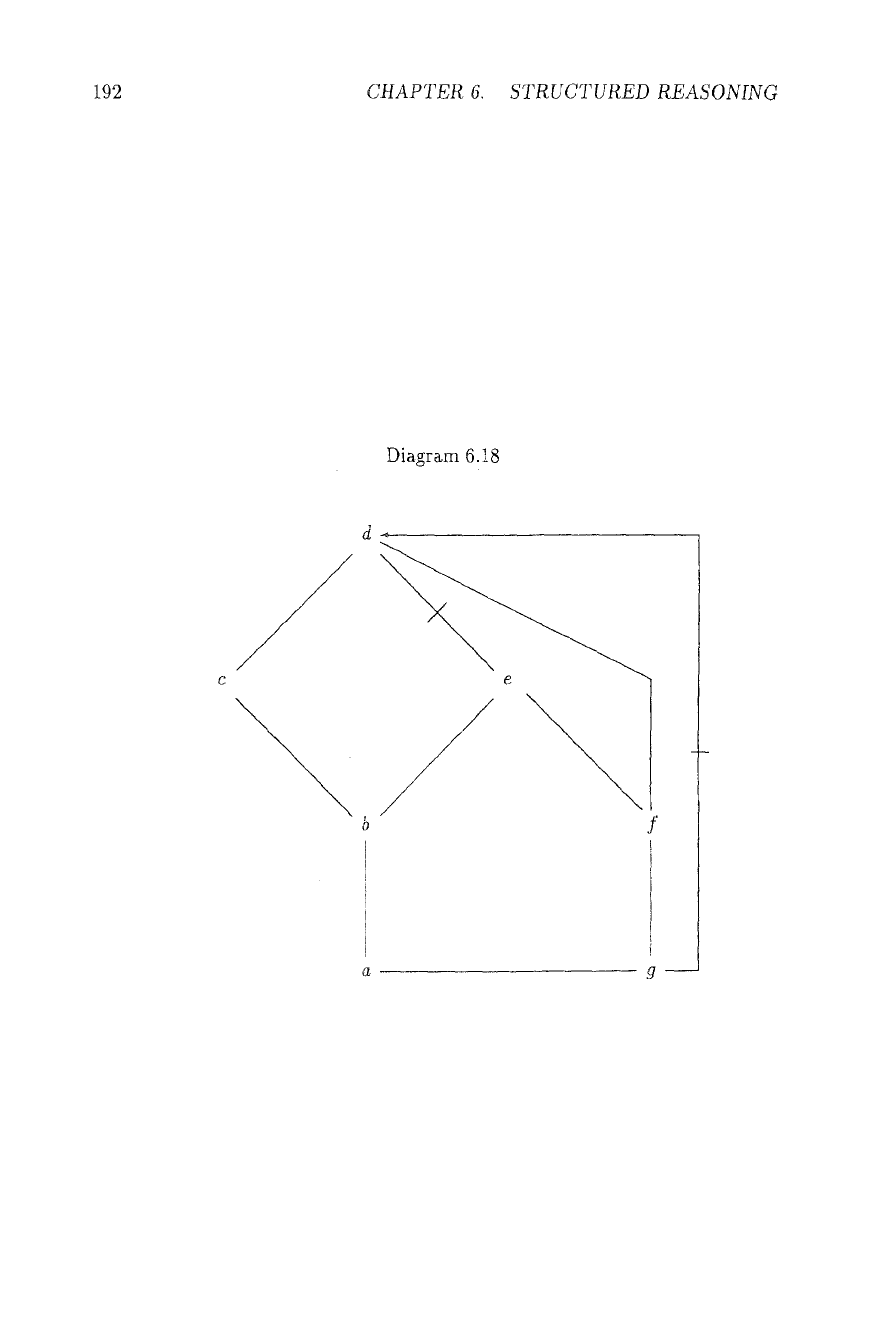
Assume we have accepted in Diagram 6.18 b + e 74 d, and look at the potential
pathsfromatod:
a --+ b --* e 74 d, a + g --+ f -~ e 74 d, a --+ g --+ f --~ d
are precluded, a -+ b ---+ e --~ d and a --+ g 74 d are both contradicted, but
a --+ b --+ c --+ d is, in addition, vertically incoherent with b -+ e 74 d, so we
accept only one continuation of the extension, with a --~ g 74 d.
In Diagram 6.17, assume that the paths b --~ g 7/4 o, c ---+ i 74 o, d + k --+ o,
e --+ m --+ o are already admitted to the extension. Let's look at the left hand
side of the diagram. All negative paths a ~ ... 74 o are impossible (off-path
192
CHAPTER 6. STRUCTURED REASONING
d
Diagram 6.18
f
a g

6.1. INHERITANCE DIAGRAMS
193
Diagram 6.19
9
C
d
Y
~z
precluded). The positive paths ~ -~ ... --+ o are in conflictual decoupling with
b --+ g 7 4 o or c ~ i 74 o. The situation on the right-hand side is just the
opposite: all positive paths a --+ ... ~ o are precluded, all negative ones in
conflictual decoupling. All paths from a to o - which are not precluded - have the
same quality, i.e. contradicted and incoherent, so our above principle leads us
to branch into two extensions, one for the negative possibility, the other for the
positive possibility, they are simply the best choices we can make. On the other
hand, if we add a --+ p --~ o to the diagram, this results in the superior quality
of a --+ p -+ o, and, as we accept no positive support - see our above argument -
all other potential paths are rejected, and we have only one continuation of the
extension, with a + p --+ o as the only path between a and o.
A less clear situation is given by Diagram 6.19.
One might argue that a --* c -+ g is also in conflictual decoupling with d --+ h 74 g
(as the "smooth" possibility a --+ d ~ h 74 g is open).
In this context, the question might arise whether we should introduce here new
truth values for accepted paths. But, this would contradict the principles of
standard extension based inheritance, as can be seen e.g. by the following diagram
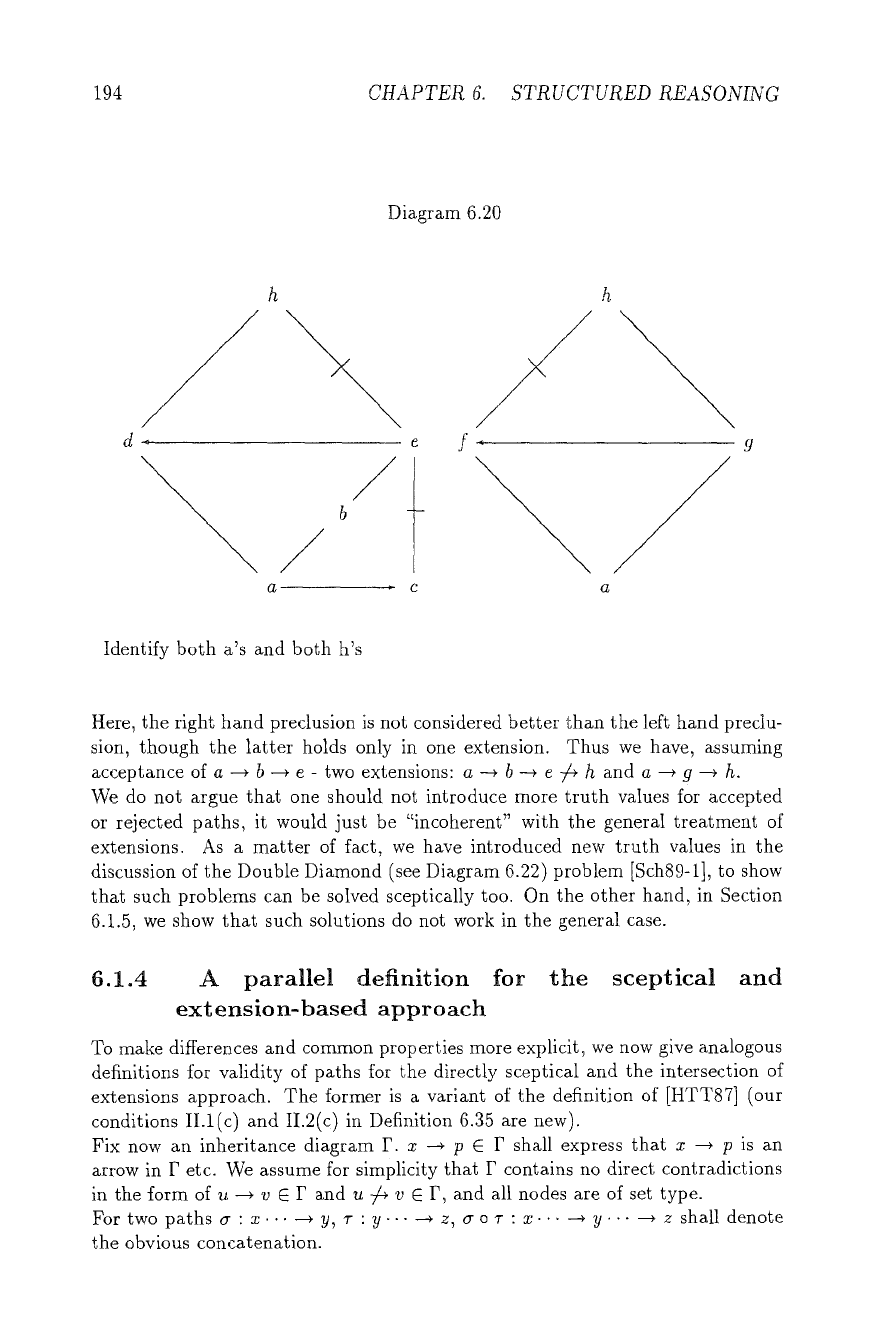
(an analogue of the Double Diamond, Diagram 6.22) in Diagram 6.20.
194
CHAPTER 6. STRUCTURED REASONING
Diagram 6.20
h
d4
Y
a
h
a
Identify both a's and both h's
Here, the right hand preclusion is not considered better than the left hand preclu-
sion, though the latter holds only in one extension. Thus we have, assuming
acceptance of a --* b --+ e - two extensions: a --* b --~ e -/+ h and a --* g --~ h.
We do not argue that one should not introduce more truth values for accepted
or rejected paths, it would just be "incoherent" with the general treatment of
extensions. As a matter of fact, we have introduced new truth values in the
discussion of the Double Diamond (see Diagram 6.22) problem [Sch89-1], to show
that such problems can be solved sceptically too. On the other hand, in Section
6.1.5, we show that such solutions do not work in the general case.
6.1.4 A parallel definition for the sceptical and
extension-based approach
To make differences and common properties more explicit, we now give analogous
definitions for validity of paths for the directly sceptical and the intersection of
extensions approach. The former is a variant of the definition of [HTT87] (our
conditions II.l(c) and II.2(c) in Definition 6.35 are new).
Fix now an inheritance diagram F. z ~ p E F shall express that z --* p is an
arrow in F etc. We assume for simplicity that F contains no direct contradictions
in the form of u --~ v E F and u 74 v E F, and all nodes are of set type.
For two paths cr : x... --+ y, T : y--- ~ z, c~ o r : x... --+ y... ~ z shall denote
the obvious concatenation.

6. i. INHERITANCE DIAGRAMS
195
Definition 6.33 (Generaiized and Potential Paths)
a) Generalized paths:
If x -~ p E P, then x ~ p is a generalized path,
if x 7# p E F, then z ?4 p is a generalized path.
If z-.. --+ p is a generalized path, and p --~ q~ E F, then z-.- ~ p --~ q is a
generalized path,
if z.-' --+ p is a generalized path, and p 7# q E F, then z.-. --~ p 7# q is a
generalized path.
b) Potential paths:
If x --~ p E F, then z -~ p is a positive potential path (pp.),
if z 7# p E P, then z 7# p is a negative pp.
If x-.. --* p is a positive pp., and p --+ q E P, then x-.. --+ p --~ q is a positive
pp.,
if z.-- --~ p is a positive pp., and p 7# q E P, then z--. ~ p 7# q is a negative
pp. []
Thus a generalized path is a potential one iff all arrows except possibly the last
one are positive. It is easy to see by our intuitive reading that only potential
paths can correspond to reasonable arguments.
Up to the end of this Section 6.1.4, Definition 6.37, we fix some node z in F
and define the valid paths and preclusions starting in x for the directly sceptical
and the extensions approach. We start by the auxiliary notion of degree (relative
to z), a mapping f from the vertices to natural numbers such that p --* q or
p 7# q E P implies
f(p) < f(q).
Definition 6.34
(Degree)
Let c be a generalized path beginning in x, ending in y, then degr(a) :=
degr(y)
:= the maximal length of any generalized path beginning in z and ending in y. []
Let now some enumeration p of all nodes y of F for which there exists a generalized
path o" : x.-- --~ y be given, such that p respects
degp ,
i.e.
degr(y) < degr(y/)
p(y)
< p(y/). (If
degr(y) = degr(y/),
then the order of
p(y)
and
p(y/)
does not
matter.) All inductions are now performed with respect to this enumeration p.
Definition 6.35 (Directly SkepticaI Approach, Preclusion and Validity)
We define by simultaneous induction validity of paths and results in F, denoted
F ~ a (F ~-
zy/F ~ :c~),
and preclusion in F. Assume that y is the first node in
the enumeration p which has not yet been treated.
1) Preclusion in F
A pp. ~r : z... --~ y is said to be precluded in F iff
(a) Zength(~) > 1 and,
(b)
Case 1, ~r is positive: either z 7# y E F or there is u such that a : z..- ~ u -~ y
and a positive pp. 7- : x.-. ~ z-.. ~ u tbr some z such that (1) F ~ r (thus, we
accept that z is more specific than z~, as seen from z - note that F ~ 7" has already

196
CHAPTER 6. STRUCTURED REASONING
been decided by induction hypothesis), (2) z 74 !/E P (we have a contradiction,
which, by (1) is stronger than u -~ y).
Case 2, c~ is negative: analogous, i.e. either x --+ 9 E F or there is u such that
(r : x... --* u 74 y and a positive pp.
r : z... --~ z... --* "u
for some z such that
(1) r ~,, (2) z-~yEr.
2) Validity of Paths:
Let cr : z-.- --~ y be a potential path. (Valid paths have to be potential paths.)
Case I: (r is a direct link in r. Then F ~ a.
Case II: cr is a potential path of length > 1. (Note that by induction hypothesis,
F ~ ~- is decided for all ~- with degree less than
degc(~r).)
Case II.l: ~r is a positive pp. z... --~ u --~ y, let r : x... ~ u be its initial
segment. Then F ~ r iff (a) r ~ v (the initial segment must be a valid path -
decided already, by induction hypothesis), (b) ~ -* y E F, (c) cr is not precluded
in F, (d) if there is a positive pp. ~'/:= z..- --* v such that I" ~ rt and v 74 y E F,
then er := rl o v 74 y is precluded in F (preclusion of conflicting paths).
The following diagram 6.21 illustrates preclusion of a conflicting path.
Case II.2: The negative case is entirely symmetrical, c~ is a negative pp. x... -~
u 74 y, let again ~-: x... --* u be its initial segment. Then r ~ ~r iff (a) r ~ r, (b)
u 74 y E P, (c) c~ is not precluded in F, (d) if there is a positive pp. ~'I := z..- --~ v
such that P ~ ~-/and v ~ 9 E F, then ~r/:= rl o v -~ y is precluded in r.
3) Validity of Results: Finally, we define r ~
zy
iff there is a positive pp.
c~ : x... -* y such that r ~ c~, likewise F ~ x~, iff there is a negative pp.
cr:z...74ysuchthatF~r
Note that by II.l(a) and II.2(a), this formalism works by upward chaining of argu-
ments, there are other formalisms, which work downwards. For more information,
the reader is referred e.g. to [Sch92-tl].
We now transform this approach into an analogous one via extensions (this is
not included in [HTT87], but our ad hoc definition). We inductively construct
the extensions of F, which are sets of paths. For uniformity of notation, we shM1
continue to write E ~ cr for cr E E, if c~ is a path in the extension E.
Definition 6.36 (Extensions Approach, Preclusion and Validity)
We start with one empty extension, s := {~}. The construction proceeds in two
directions: First, each extension constructed so far grows by adding new paths as
valid, second, the number of extension may grow as the construction splits one
extension into two differently developing cases.
We assume to have (partially) constructed s := {E~ : i E I} so far, by considering
all nodes prior to y in the enumeration p. The following operation for y will be
performed simultaneously (or successively) on all
Ei,
so we fix one such partially
constructed E
:= El.
Again, we define by simultaneous induction ~preclusion and validity of paths.
Many comments carry over from the directly sceptical case, we do not repeat
them here.
1) Preclusion in extension (analogous to preclusion in P):
A pp. ~ : x.-. -~ y is said to be precluded in E iff
