Schlick T. Molecular Modeling and Simulation: An Interdisciplinary Guide

Подождите немного. Документ загружается.

280 9. Force Fields

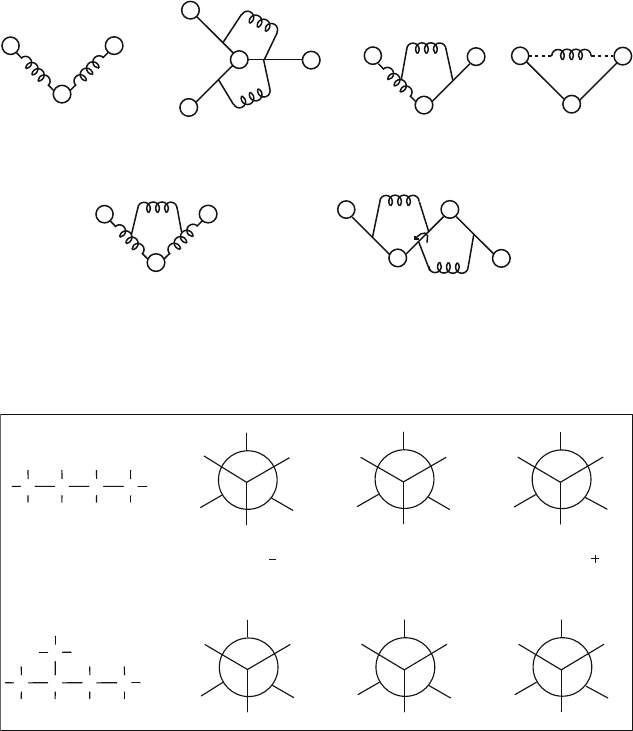
stretch/stretch

bond angle/dihedral/bond angle

stretch/bend/stretch

bend/bend

stretch/bend

Figure 9.7. Schematic illustrations for various cross terms involving bond stretching, angle

bending, and torsional rotations.

n - butane

2-methylbutane

HHH

gauche

trans

(anti)

gauche

CCC

CCCC

Figure 9.8. Torsional orientations for n-butane and 2-methylbutane, as illustrated by

Newman projections viewed along the central C–C bond. Note that while n-butane has

the global minimum at the trans (or anti) conﬁguration, the gauche states of 2-methylbu-

tane are lower in energy than the corresponding trans (symmetrical) state since the methyl

groups are better separated and hence the molecule is less congested.

It is commonly used in molecular mechanics force ﬁelds, like CHARMM. The

potential is a simple harmonic function of the interatomic (not bond) distance ρ,

between atoms i and k in the bonded ijk sequence (see Figure 9.7):

(ρ)=S [ρ − ¯ρ] . (9.22)

9.5. Torsional Potentials 281

9.5 Torsional Potentials

9.5.1 Origin of Rotational Barriers

Torsional potentials are included in potential energy functions since all the

previously described energy contributions (nonbonded, stretching, and bending

terms) do not adequately predict the torsional energy of even a simple molecule

such as ethane. In ethane, the C–C bond provides an axis for internal rotation of

the two methyl groups.

Although the origin of the barrier to internal rotation has not been resolved

[472, 1010, 1360],

explanations involve the relief of steric congestion and opti-

mal achievement of resonance stabilization (another quantum-mechanical effect

arising from the interactions of electron orbitals) [1010]. This latter consideration

represents a newer hypothesis. For a long time, the primary interactions that give

rise to rotational barriers have been thought to be repulsive interactions, caused

by overlapping of bond orbitals of the two rotating groups [1002].

In ethane (C

), for example, the torsional strain about the C–C bond is

highest when the two methyl groups are nearest, as in the eclipsed or cis state,

and lowest when the two groups are optimally separated, as in the anti or trans

state (see Figure 9.8 and the related illustration for n-butane in Figure 3.13 of

Chapter 3). Without a torsional potential in the energy function, the eclipsed form

for ethane is found to be higher in energy than the staggered form, but not suf-

ﬁciently higher to explain the observed staggered preference [24]. See [27]fora

meticulous theoretical treatment of the torsional potential of butane, showing that

a large basis set combined with a treatment of electron correlations in ab initio

calculations is necessary to obtain accurate equilibrium energies relative to the

anti conformation.

Accounting accurately for rotational ﬂexibility of atomic sequences is impor-

tant since rotational states affect biological reactivity. Such torsional parameters

are obtained by analyzing the energetic proﬁle of model systems as a function of

the ﬂexible torsion angle. The energy differences between rotational isomers are

used to parameterize appropriate torsional potentials that model internal rotation.

9.5.2 Fourier Terms

The general function used for each ﬂexible torsion angle τ has the form

(τ)=



[1 ± cos nτ] , (9.23)

where n is an integer. For each such rotational sequence described by the tor-

sion angle τ, the integer n denotes the periodicity of the rotational barrier, and

Goodman et al. [472] refer to the barrier origin as “the Bermuda Triangle of electronic the-

ory”, reﬂecting a complex interdependence among three factors: electronic repulsion, relaxation

mechanisms, and valence forces.

282 9. Force Fields

is the associated barrier height.Thevalueofn used for each such torsional

degree of freedom depends on the atom sequence and the force ﬁeld parameteri-

zation (see below). Typical values of n are 1, 2, 3 (and sometimes 4). Other values

(e.g., n =5, 6) are used in addition by some force ﬁelds (e.g., CHARMM [805]).

A reference torsion angle τ

may also be incorporated in the formula, i.e.,

(τ)=



[1 + cos(nτ −τ

)] . (9.24)

Often, τ

= 0orπ and thus the cosine expression of form (9.23) sufﬁces; this is

because eq. (9.24) can be reduced to the form of eq. (9.23) in such special cases,

from relations like:

1+cos(nτ −π)=1− cos(nτ) .

Experimental data obtained principally by spectroscopic methods such as

NMR, IR (Infrared Radiation), Raman, and microwave, each appropriate for var-

ious spectral regions, can be used to estimate barrier heights and periodicities in

low molecular weight compounds. According to a theory developed by Pauling

[972], potential barriers to internal rotation arise from exchange interactions of

electrons in adjacent bonds; these barriers are thus similar for molecules with the

same orbital character. This theory has allowed tabulations of barrier heights as

class averages [871, 898, 1152, 1153]. Since barriers for rotations about various

single bonds in nucleic acids and proteins are not available experimentally, they

must be estimated from analogous chemical sequences in low molecular weight

compounds.

9.5.3 Torsional Parameter Assignment

In current force ﬁelds, these parameters are typically assigned by selecting several

classes of model compounds and computing energies as a function of the torsion

angle using ab initio quantum-mechanical calculations combined with geometry

optimizations. The ﬁnal value assigned in the force ﬁeld results from optimization

of the combined intramolecular and nonbonded energy terms to given experimen-

tal vibrational frequencies and measured energy differences between conformers

of model compounds.

This procedure often results in several Fourier terms in the form (9.23), that is,

several {n, V

} pairs for the same atomic sequence; see examples in Table 9.3.

Moreover, parameters for a given quadruplet of atoms may be deduced from

more than one quadruplet entry. For example, the quadruplet C1



–C2



–C3



–O3



in nucleic acid sugars may correspond to both a C1



–C2



–C3



–O3



entry and

a –C–C– entry, the latter designating a general rotation about the endocyclic

sugar bond; here,  designates any atom. When general rotational sequences are

involved (e.g., –C–N–), CHARMM may list a pair of {V

,τ

} values (i.e.,

different τ

for the same rotational term); only one τ

is used when a speciﬁc

quadruplet atom sequence is speciﬁed.

9.5. Torsional Potentials 283

Twofold and Threefold Sums

Twofold and threefold potentials are most commonly used (see Figure 9.9 for

an illustration). Inclusion of a one-fold torsional term as well is a force-ﬁeld

dependent choice.

A threefold torsional potential exhibits three maxima at 0

, 120

, and 240

and three minima at 60

, 180

, and 300

. Ethane has a simple 3-fold torsional

energy proﬁle, as seen in the 3-fold energy curve in Figure 9.9, with all maxima

energetically equivalent and corresponding to the eclipsed or cis form, and all

minima corresponding to the energetically equivalent staggered or trans form.

In related hydrocarbon sequences, the local minima may not be of equal

energies. For n-butane, for example, the anti (or trans) conformer is roughly

1 kcal/mol lower in energy than the two gauche states. In 2-methylbutane, the

gauche states are lower in energy than the anti state due to steric effects. The

torsional conformations of these molecules are illustrated in Figure 9.8.

In general, the gauche forms may be higher in energy than the trans form, as

in n-butane [1153], or lower in energy, as in 2-methylbutane due to steric effects.

Certain X–C–C–Y atomic sequences where the X or Y atoms are electronega-

tive like O or F (e.g., 1-2-diﬂuoroethane, certain O–C–C–O linkages in nucleic

acids) [532] also have lower-in-energy gauche conformations, but this is due to a

fundamentally different effect than present in hydrocarbons — neither steric, nor

dipole/dipole — called the gauche effect [532].

Reproduction of Cis/Trans and Trans/Gauche Energy Differences

A combination of a twofold and a threefold potential can be used to reproduce

both the cis/trans and trans/gauche energy differences. Figure 9.9 illustrates the

case for different parameter combinations of the twofold and threefold parame-

ters. One interaction is modeled after the O–C–C–O sequence in nucleic acids

(e.g., O3



–C3



–C2



–O2



in ribose) [937], showing a minimum at the trans state.

The other is a rotation about the phosphodiester bond (P–O) in nucleic acids,

showing a shallow minimum at the trans state. Note that for small molecules, tor-

sional potentials with n =1, 2, 3, 4 and 6 are often used to reproduce torsional

frequencies accurately.

To see how to combine twofold and threefold torsional potentials, for example,

denote the experimental energy barrier by ΔV , the total empirical potential en-

ergy function as E,andletE

represent the following combination of twofold

and threefold torsional terms:

[1 + cos 2τ]+

[1 + cos 3τ] . (9.25)

The torsional parameters V

and V

for a given rotation τ are then computed from

the relations:

ΔV

cis/trans

= E

τ =0

− E

τ =180

= V

+[E − E

]

τ =0

− [E − E

]

τ =180

(9.26)

284 9. Force Fields

ΔV

trans/gauche

= E

τ =180

− E

τ =60

=(3V

)/4+[E − E

]

τ =180

− [E − E

]

τ =60

(9.27)

since

= E

τ =0

− E

τ =180

and

= E

τ =180

− E

τ =60

Thus, Cartesian coordinates of the molecule must be formulated in terms of τ.

A simpliﬁcation can be made by assuming ﬁxed bond lengths and bond angles

and calculating nonbonded energy differences only. In theory, then, every differ-

ent parameterization of the nonbonded coefﬁcients requires an estimation of the

torsional potentials V

and V

to produce a consistent set.

This general requirement in development of consistent force ﬁelds explains why

energy parameters are not transferable from one force ﬁeld to another.

In general, many classes of model compounds must be used to represent

the various torsional sequence in proteins and nucleic acids. Since rotational

barriers in small compounds have little torsional strain energy compared with

large systems, rotational proﬁles are routinely computed for a series of substi-

tuted molecules. Substituted hydrocarbons are used, for example, to determine

rotational parameters for torsion angles about single C–C bonds in saturated

species.

50 100 150 200 250 300 350

0.5

1.5

2.5

O5'

C5'

50 100 150 200 250 300 350

O3'

C3'

C2'

O2'

2 fold

3 fold

sum

τ (dihedral angle) [deg.]

Dihedral angle energy [kcal/mol]

Figure 9.9. Twofold and threefold torsion-angle potentials and their sums for an O–C–C–O

rotational sequence in nucleic-acid riboses (V

= 1.0 and V

= 2.8 kcal/mol, reproducing

the known trans/gauche energy difference [937]) and a rotation about the phosphodiester

(P–O) bond in nucleic acids (V

= 1.9 and V

= 1.0 kcal/mol, from CHARMM [805]).

9.5. Torsional Potentials 285

Model Compounds

Examples of model compounds used for assigning torsional parameters to nucleic

acids and proteins include the following (see Figure 9.10).

• Hydrocarbons like ethane, propane,andn-butane, and the more crowded

environments of 2-methylbutane and cyclohexane: for rotations about sin-

gle C–C bonds in saturated species (i.e., each carbon is approximately

tetrahedral), such as C–C–C–C, H–C–C–H, and H–C–C–C;

• The ethylbenzene ring: for rotations about CA–C bonds in ring systems

(CA denotes an aromatic carbon);

• Alcohols like methanol and propanol: to model H–C–O–H, C–C–O–H,

H–C–C–O, and C–C–C–O sequences (e.g., in the amino acids serine and

threonine);

Ethane

Propane

n-Butane

2-Methylbutane

Cyclohexane

Ethylbenzene

Methanol

Propanol

SCCC

SCH

Methyl Propyl Sulfide

CSC

SCH

Dimethyl Sulfide

Methylamine

CHO

Ethanal (acetaldehyde)

CNC

NHCHO

n-Methyl formamide

CCC

CCCC

Figure 9.10. Model compounds for determining torsional parameters for various atomic

sequences in biomolecules. Illustrated in bold is τ : the bond about which the τ rotation

occurs, or the complete τ sequence (3 bonds), as needed for an unambiguous deﬁnition.

286 9. Force Fields

• Sulﬁde molecules (e.g., methyl propyl sulﬁde): to model rotations

involving sulfur atoms (e.g., C–C–C–S, C–C–S–C, and H–C–S–C) as in

methionine, or dimethyl disulﬁde (C–S–S–C), to model disulﬁde bonds in

proteins;

• Model amine, aldehydes, and amides (e.g., methylamine, ethanal,

N-methyl formamide): for sequences involving nitrogens such as

H–C–N–H, H–C–C=O, and H–C–N–C.

See [842] for a comprehensive description of such a parameterization for peptides

based on ab initio energy proﬁles.

In the CHARMM and AMBER force ﬁelds, the parameters n and V

are

highly environment dependent. Furthermore, more than one potential form can

be used for the same bond about which rotation occurs; these different torsion-

angle terms may be weighted proportionately. Some examples of torsion angle

parameters from the AMBER [265] and CHARMM [805, 809]forceﬁeldsare

given in Table 9.3.

Table 9.3. Parameters for selected torsional potentials from the AMBER (ﬁrst row for each

sequence) [218] and CHARMM (second row of that sequence) [415, 805]forceﬁelds.

Barrier heights are in units of kcal/(mol rad

), angles are in radians, and  represents

any atom.

SEQUENCE

DESCRIPTION

–C–C– 1.4 0 alkane C–C (e.g., Lys

0.2 0 or Leu C

–C

)



–C1



–N9–C8 2.5 0 purine glycosyl

1.1 0 C1



–N9 rotation (A, G)

C–C–S–C 1.0 0 rotation about C–S

0.24 π 0.37 0 in Met



–P–O5



–C5



1.2 0 0.5 0 P–O5



rotation in

1.2 π 0.1 π 0.1 π nucleic-acid backbone

9.5.4 Improper Torsion

Harmonic ‘improper torsion’ terms, also known as ‘out-of-plane bending’ poten-

tials, are often used in addition to the terms described above to improve the overall

ﬁt of energies and geometries. They can enforce planarity or maintain chirality

about certain groups. The potential has the form

(χ)=(V



/2) χ

, (9.28)

9.5. Torsional Potentials 287

’

Wilson angle

improper/improper

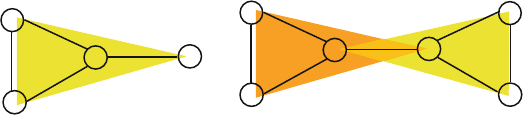
Figure 9.11. Wilson angle deﬁnition (left) and geometry for a cross improper/improper

torsion term (right).

where χ is the improper Wilson angle. It is deﬁned for the four atoms i, j, k, l for

which the central j is bonded to i, l, and k (see Figure 9.11) as the angle between

bond j–l and the plane i–j–k.

The following are examples of atom centers used to deﬁne sequences of atoms

counted in improper torsion potentials (taken from CHARMM):

• Polypeptide backbone nitrogen and carbonyl carbons attached to the C

atom (i.e., N and C in the sequence –N–C

–C=O), for maintaining

planarity of the groups around the peptide bond;

• Terminal side-chain carbons in the CO

unit of the Asp and Glu amino

acids;

• Terminal side-chain carbons in the O=C–NH

unit of the Asn and Gln

amino acids;

• Terminal side-chain carbon in the NH

–C–NH

unit of the Arg amino acid;

• Various carbons and nitrogens in the side-chain rings of the Phe; Tyr, and

Trp amino acids (not used in all CHARMM versions);

• Glycosyl nitrogen (N1 in pyrimidines or N9 in purines) in nucleic acid

bases;

• Exocyclic nitrogen of the NH

unit attached to the aromatic ring of the

adenine and cytosine bases in nucleic acids (N6 in adenine and N4 in

cytosine).

9.5.5 Cross Dihedral/Bond Angle and Improper/Improper

Dihedral Terms

Cross terms are used in certain force ﬁelds (e.g., CVFF used in the In-

sight/Discover program) to model various relationships between quadruplet

sequences (see Figure 9.11) or to couple torsion angles with bond angles or torsion

angles with bond lengths (see Figure 9.7). For example, the association between

a torsion angle and related bond angles can take the form

τθθ



(τ,θ,θ



)=KV

τθθ



cos τ [θ −

θ][θ



−



] . (9.29)

288 9. Force Fields

This kind of potential couples the two bending motions (e.g., symmetric and

antisymmetric wagging of the two methyl groups in ethane) and has an important

affect on spectra (vibrational frequencies). A cross term that relates the dihedral

angle to one bond angle can, however, have instead a large effect on geometry

(with a small effect on spectra):

τθ

(τ,θ)=KV

τθ

cos τ [θ −

θ] . (9.30)

(More generally, cos τ above may be replaced by a Fourier series in the form of

eq. (9.23)oreq.(9.24)).

This torsion/bend effect may be important to reproduce ﬁne features like a

small C–C–H bond-angle opening in the eclipsed conﬁguration in ethane relative

to the staggered conﬁguration.

Torsion/stretch potentials can similarly be used for ﬁne tuning, for exam-

ple to reproduce a bond-stretching tendency for ethane in the eclipsed torsional

conﬁguration (relative to the staggered-conﬁguration bond length) [30].

The association between neighboring Wilson angles, in which the two centers

(j and j



) are bonded, can be represented as:

χχ



(χ, χ



)=V

χχ



χχ



. (9.31)

9.6 The van der Waals Potential

9.6.1 Rapidly Decaying Potential

The van der Waals potential for a nonbonded distance r

has the common 6/12

Lennard-Jones form in macromolecular force ﬁelds:

−A

, (9.32)

where the attractive and repulsive coefﬁcients A and B depend on the type of

the two interacting atoms. The attractive r

−6

term originates from quantum me-

chanics, and the repulsive r

−12

term has been chosen mainly for computational

convenience. Together, these terms mimic the tendency of atoms to repel one an-

other when they are very close and attract one another as they approach an optimal

internuclear distance (Figure 9.12).

As mentioned in the last chapter, the 6/12 Lennard Jones potential represents

a compromise between accuracy and computational efﬁciency; more accurate ﬁts

over broader ranges of distances are achieved with the Buckingham potential [30,

766]: −A

+ B

exp(−B



The steep repulsion has a quantum origin in the interaction of the electron

clouds with each other, as affected by the Pauli-exclusion principle, and this

combines with internuclear repulsions.

9.6. The van der Waals Potential 289

The weak bonding attraction is due to London or dispersion force (in quantum

mechanics this corresponds to electron correlation contributions). Namely, the

rapid ﬂuctuations of the electron density distribution around a nucleus create a

transient dipole moment and induce charge reorientations (dipole-induced dipole

interactions), or London forces.

Note that as r →∞, E

→ 0 rapidly, so the van der Waals force is short

range. For computational convenience, van der Waals energies and forces can be

computed for pairs of atoms only within some “cutoff radius”.

9.6.2 Parameter Fitting From Experiment

Parameters for the van der Waals potential can be derived by ﬁtting parameters

to lattice energies and crystal structures, or from liquid simulations so as to re-

produce observed liquid properties [265]. From crystal data, minimum contact

distances {r

}of atom radii (see below) can be obtained. Liquid simulations, such

as by Monte Carlo, are typically performed on model liquid systems (e.g., ethane

and butane) to adjust empirical minimum contact distances {r

} (see below) so as

to reproduce densities and enthalpies of vaporization of the liquids.

9.6.3 Two Parameter Calculation Protocols

To determine the attractive and repulsive coefﬁcients for each {ij} pair, two main

procedures can be used for each different type of pairwise interaction (e.g., C–C,

C–O).

Energy Minimum/Distance Procedure (V

)

In the ﬁrst approach, coefﬁcients can be obtained by requiring that an energy min-

imum V

will occur at a certain distance, r

, equal to the sum of van der Waals

radii of atoms i and j. This requirement between the minimum energy and

distances produces the relations:

=2(r

)

(9.33)

and

=(r

)

. (9.34)

The latter equation can be written using eq. (9.33)intermsofA

and r

)

. (9.35)

The van der Waals radii can be calculated from the measured X-ray contact

distances — which reﬂect the distance of closest approach in the crystal. These

contact distances are appreciably smaller than the sum of the van der Waals radii

of the atoms involved. This relationship — between the X-ray contact distances,

which crystallographers refer to as “van der Waals radii”, and the molecular

mechanics meaning of van der Waals radii — was recognized in the early days of

molecular mechanics [28,1345] but still may not be widely appreciated.