Schlick T. Molecular Modeling and Simulation: An Interdisciplinary Guide

Подождите немного. Документ загружается.

270 9. Force Fields

Table 9.1. Characteristic stretching vibrational frequencies.

Vibrational Mode Frequency [cm

−1

]

H–O stretch 3600–3700

H–N stretch 3400–3500

H–C stretch 2900–3000

H–Br stretch 2650

C≡C, C≡N stretch 2200

C=C, C=O stretch 1700–1800

C–N stretch 1250

C–C stretch 1000

C–S stretch 700

S–S stretch 500

Table 9.2. Characteristic bending and torsional vibrational frequencies.

Vibrational Mode Frequency [cm

−1

]

H–O–H, H–N–H bend 1600

H–C–H bend 1500

H–C–H scissor 1400

H–C–H rock 1250

H–C–H wag 1200

H–S–H bend 1200

O–C=Obend 600

C–C=Obend 500

S–S–C bend 300

C=C torsion 1000

C–O torsion 300–600

C–C torsion 300

C–S torsion 200

Vibrational spectra of alkane molecules are a good source of parameters for

C–C and C–H vibrational modes in proteins and nucleic acids. The spectrum of a

butane molecule (CH

–CH

), for example, reﬂects both methyl (CH

)

and methylene (CH

) stretching and bending modes.

The alkane frequencies can be grouped into two strong stretching modes

slightly below 3000 cm

−1

, symmetric and asymmetric bending deforma-

tions within the range 1350–1500 cm

−1

, and a C–C stretching mode around

1000 cm

−1

. Indeed, these ranges of modes are evident in simulation-computed

9.2. Normal Modes 271

0 500 1000 1500 2000 2500 3000 3500 4000

Protein Water

Wave number [cm

−1

]

0 500 1000 1500 2000 2500 3000 3500 4000

Wave number [cm

−1

]

Figure 9.2. Characteristic frequencies calculated over 5 ps molecular dynamics simulations

of solvated BPTI for the protein (left) and water (right) atoms. Data are from [1089].

spectra corresponding to a small solvated protein, bovine pancreatic trypsin

inhibitor (BPTI) as seen in Figure 9.2 [1089].

9.2.4 In-Plane and Out-of-Plane Bending

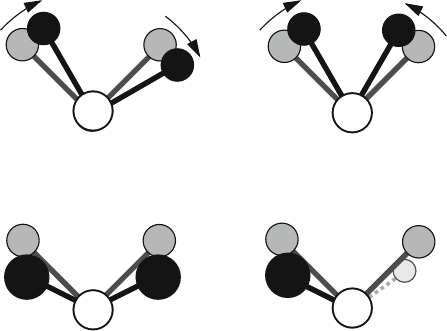
Bending modes include two types of in-plane deformations: scissoring and rock-

ing, and two out-of-plane deformations: wagging and twisting (see Figure 9.3).

The in-plane scissoring deformation of an X–Y–Z sequence makes atoms X

and Z move closer together. The rocking deformation moves both atoms in one

direction while keeping their distance about the same.

The out-of-plane wagging bending deformation moves these atoms in the same

direction with respect to the reference plane. Twisting moves one atom in one

direction and the other in the opposite direction.

Figure 9.2 shows the power spectrum of a solvated protein system (BPTI) as

computed from Fourier transforms of velocity autocorrelation functions [1089].

The calculated peak locations depend sensitively on the force ﬁeld, assuming the

simulation protocol and frequency calculation procedure are sound.

For water, we note in Figure 9.2 characteristic peaks for vibrational modes of

stretching around 3500 cm

−1

and bending around 1700 cm

−1

,aswellasthe

Essentially, vibrational spectra can be computed from molecular dynamics simulations by trans-

forming time-dependent properties, such as velocity autocorrelation functions, into the frequency

domain using Fourier transforms. See [1089], for example, for the precise procedure.

The simulation-derived peak heights can, at best, reproduce frequency values corresponding to

the force ﬁeld parameters, not the experimental values, though the latter often serve as a reference. For

example, the bond stretching force constant used for O–H water bonds may be physically unrealistic,

so an unnatural spectral peak may emerge from simulations using unconstrained O–H bonds. (The

peak is absent if these bonds are constrained).

272 9. Force Fields

in−plane

"rocking"

in−plane

"scissoring"

out−of−plane

"wagging"

out−of−plane

"twisting"

Figure 9.3. Various in-plane and out-of-plane bending vibrational modes. The reference

molecular position is shown with grey-shaded atoms, and the position after the move is

shown in black (and very-light grey for twisting). For the wag, the two nonbonded atoms

move out of the paper plane toward us, while for twist one atom moves up (toward us) and

the other down (away from us, below the paper plane).

slower tumbling or rocking (librational) motion for the water molecules as a

whole in liquid water. For the protein, a wide range of vibrations is captured,

from the fastest stretching modes for bonds involving hydrogens (O–H and N–H)

around 3300 cm

−1

to various angle-bending modes below 1700 cm

−1

,tomuch

slower deformations.

9.3 Bond Length Potentials

Bond length potentials can be considered as “strain” terms that model small-scale

deviations about reference values. The reference values for different chemical

bonds can be obtained from solved X-ray crystal structures as well as from

quantum mechanical solutions to equilibrium structures of small molecules. For

accepted values, see organic chemistry textbooks such as [878] and Handbooks

of Chemistry and Physics (e.g., CRC Press Handbook of Chemistry and Physics).

Note that ab initio methods calculate equilibrium bond lengths whereas exper-

imentally measured values are usually vibrationally averaged bond lengths; the

averaging depends on the experiment and hence there are many bond length val-

ues in theory. See [795, 797, 798] for a discussion of these different procedures

for determining bond lengths and for the interconversion among the bond length

values. For macromolecules, these small differences among the reference values

are not usually important.

9.3. Bond Length Potentials 273

9.3.1 Harmonic Term

The harmonic potential modeled after Hooke’s law is the simplest molecular-

mechanics formulation for bond deformations. According to Hooke’s law, the

force F is proportional to the displacement, x, and the acceleration, ¨x, as follows:

F (x)=−kx = m

,k= mω

> 0 . (9.1)

Thus, the angular frequency ω (number of radians per unit time), or 2π times the

circular frequency ν (= c/λ where c is the speed of light and λ is the wavelength),

is related to the spring constant k as:

ω ≡ 2πν =



k/m. (9.2)

The corresponding potential energy E is:

E(x)=

. (9.3)

More generally, we write this harmonic bond potential as:

harmonic

(r)=S

[r − ¯r]

, (9.4)

where r is the bond length, ¯r is the reference bond-length value, and S

is a

constant. From the measured mass and frequency for a particular bond vibra-

tion, force constants can be derived accordingly (k = mω

). For atomic pairs of

different species (with masses m

, m

), the general guideline is

k = μω

, (9.5)

where μ is the reduced mass deﬁned as:

μ =(m

)/(m

+ m

) . (9.6)

The harmonic potential is only adequate for small deviations from reference

values, around one vibrational level above the ground state, or on length defor-

mations of the order of 0.1

A or less. It is not valid for larger deviations from

equilibrium since the atoms dissociate and no longer interact; thus the energy

levels off, rather than increases, rapidly as the distance increases beyond ¯r.For

very small interaction distances, however, the deformation energy is very large.

This physical picture is described by a parabolic potential-well shape for small

distance separations and a leveling curve for separations greater than the ref-

erence value. Rather than a harmonic function, the precise shape of E(r) is

more adequately represented by higher-order functions that approximate better

the experimentally-measured energy trend as a function of distance.

Electronic spectroscopy is necessary to measure this precise distance depen-

dency since frequencies and energies are higher for changes in electronic states.

Speciﬁcally, the potential energy as a function of internuclear separation for

both the ground and excited states is obtained from visible and ultraviolet (UV)

274 9. Force Fields

spectroscopic techniques.

The commonly used ultraviolet and visible spectrom-

eters measure absorption of light in the range 200–750 nm. Visible and UV

absorption bands are broad since several vibrational states are contained in each

electronic state, and each vibrational state is further decomposed into many

rotational states. Thus, a rigorous assignment of bands to speciﬁc transitions is

difﬁcult, but the overall shape of the energy well can be deduced.

9.3.2 Morse Term

To model bond deformations that exceed very small ﬂuctuations about equilib-

rium states, the empirical bond potential due to P.M. Morse [879] has proven very

successful for reproducing vibrational levels of small molecules [764,1201]. The

Morse function has the form:

Morse

(r)=D{1 −exp[−S

(r − ¯r)]}

, (9.7)

where the adjustable parameters S

and D characterize the well width and well

depth respectively. As seen in Figure 9.4, the Morse potential correctly rises

steeply for contraction of the bond length (E(r) →∞as r → 0) but levels

off to the dissociation energy D at large r: E(r) → D as r →∞.

The empirical Morse potential can be written as an inﬁnite series in the powers

of the bond displacement (r − ¯r). Using Taylor series, we expand eq. (9.7)as:

Morse

(r)=D {1 −2exp[−S

(r − ¯r)] + exp[−2S

(r − ¯r)]}

= D



1 − 2



1 − S

(r − ¯r)+

(r − ¯r)

−

(r − ¯r)

+ ...





1 − 2S

(r − ¯r)+

(r − ¯r)

−

(r − ¯r)

16S

(r − ¯r)

+ ...



= DS

(r − ¯r)

− DS

(r − ¯r)

+O(r − ¯r)

. (9.8)

Hence we can relate the harmonic stiffness constant S

in eq. (9.4)totheMorse

constant S

of eq. (9.7)as:

≈ D(S

)

. (9.9)

UV spectroscopy measures wavelengths just beyond the violet end of the visible spectrum, that

is, with λ<400 nm.

9.3. Bond Length Potentials 275

0 1 2 3 4 5

100

150

200

Morse

Quartic

(special)

Cubic

...........

Quartic

Harmonic

r (bond length) [A]

Bond energy [kcal/mol]

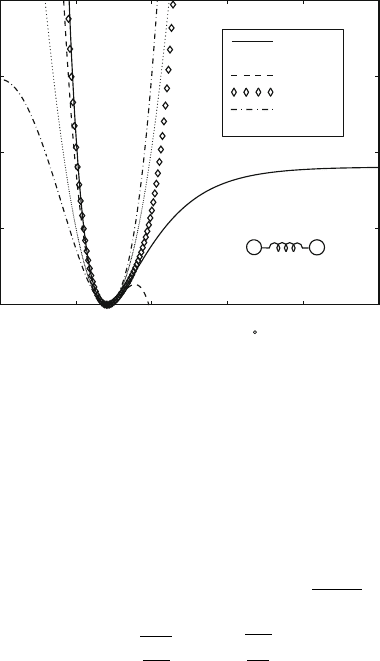
Figure 9.4. Morse, harmonic, cubic, and two quartic bond potentials for H–Br. The Morse,

harmonic, and special quartic potentials are given in eqs. (9.7), (9.4), and (9.11), respec-

tively. The cubic and non-degenerate quartic polynomials are given polynomial coefﬁcients

to match the Taylor-series expansion of the Morse potential given in eq. (9.8) up to the de-

sired order. Note that the cubic potential causes a problem for signiﬁcant bond stretches

because of the change in curvature.

Put another way, from the relationship between S

and the spring constant of a

harmonic oscillator, namely S

= k/2=(μω

)/2, the value of the Morse well-

depth parameter S

can be reasonably approximated as



/D or

= ω



= πν



2μ

. (9.10)

Figure 9.4 shows the harmonic and Morse potentials for a hydrogen bromide

molecule. The parameters D =90.5 kcal/mol, S

= 1.814

−1

, ¯r =1.41

and S

= 297.8 (kcal/mol)/

(from eq. (9.9)), are used. We note that the har-

monic potential is a good approximation to the energy surface only for small

displacements from equilibrium.

9.3.3 Cubic and Quartic Terms

To reproduce Morse potentials better than possible with the harmonic potential,

cubic and quartic polynomials can be used (through terms added to the quadratic

potential) to match the Taylor series expansion of eq. (9.8)uptoadesiredorder,

as shown in Figure 9.4. The MM3 force ﬁeld, for example, uses cubic and quartic

bond potentials, which work well for most molecules [30]; a sextic bond potential

works even better and is used in MM4. The Merck force ﬁeld, MMFF [497], uses

a quartic bond function. Note that for better optimization of the shape of the bond

276 9. Force Fields

length potential function, coefﬁcients of the polynomial can be adjusted; thus they

need not coincide with those given by the Morse Taylor expansion of eq. (9.8).

Note that a quartic is preferable to a cubic bond potential because the cubic

function has an inﬂection point at some value r>¯r; thus, signiﬁcant bond

stretches lead to negative rather than positive energy (E →−∞as r →∞)(see

Figure 9.4). This can cause the molecular energy to have large negative values

and the computation (energy minimization, for example) to become nonsensical.

Series that end in even powers (like quartic rather than cubic polynomials) can

provide better approximations and drive the molecule more rapidly toward the

energy minimum.

For large-molecule force ﬁelds where computational time is important, a spe-

cial quartic has been suggested to avoid square root computations [1101,1103]; it

measures the square of the squared bond differences as:

quartic

= S

− ¯r

]

. (9.11)

This quartic is special (degenerate)since it does not contain a cubic term. Its shape

is therefore similar to the harmonic potential, as shown in Figure 9.4.

At small displacements from equilibrium, we have the relation

− ¯r

]

≡ [r − ¯r]

[r +¯r]

≈ [r − ¯r]

(2¯r)

Hence, comparing the series expansion in eq. (9.11) with the harmonic potential of

eq. (9.4), we can relate the quartic-potential force constant to that of the harmonic

potential by:

≈ S

/4¯r

. (9.12)

Figure 9.4 displays this quartic potential with S

calculated from S

as above. As

for the quadratic potential, the energy approximation is good only for very small

deviations from equilibrium.

9.4 Bond Angle Potentials

The bond angle arrangement around each atom in a molecule is governed by the

hybridization of the orbitals around the atom. For example, when an atom has

two identical hybrid orbitals (sp) around it (e.g., Be in BeCl

), the bond angle is

180

. When three identical orbitals surround an atom (e.g., B in BF

, sp

), the ar-

rangement is trigonal and coplanar with bond angles all 120

. When four identical

orbitals surround an atom (e.g., C in CH

, sp

), the arrangement is tetrahedral —

all angles are 109.47



tet

=cos

−1

[−1/3]



This simple rule serves as a ﬁrst approximation for bond angle geometries.

However, small deviations from these estimates generally occur, and large de-

viations sometimes occur. Even small differences of 1–2

between different

bond angles in a molecule can have important global inﬂuence on molecular

structure, as in riboses.

9.4. Bond Angle Potentials 277

Indeed, it is important to realize that exact sp

orbits exist only for

tetrahedrally-symmetric compounds like methane. Ordinary alkanes already

have their orbits deformed: propane, for example, has the C–C–C bond angle of

about 112.5

and H–C–H bond angles around 107.5

; its C–C–H bond angles are

approximately tetrahedral. Another common example of bond angle deviations

involves ring molecules, like cycloalkanes and riboses; ring-closure constraints

can alter the geometry signiﬁcantly. Finally, electron lone pairs about atoms in-

ﬂuence the geometry: in water, the oxygen lone pair forms bond-like orbitals to

produce the liquid water bond angle θ(H–O–H) ≈105

. See Figure 9.5 for such

illustrations. As for bond potentials, stiffness constants for bond angle bending

are determined from measured vibrational frequencies.

9.4.1 Harmonic and Trigonometric Terms

Commonly used bond-angle potentials are harmonic functions that involve the

difference between angles and angle cosines:

harmonic

(θ)=K

[θ −

θ]

, (9.13)

trig.

(θ)=K

[cos θ −cos

θ]

. (9.14)

As shown above for bond potentials, we can expand the trigonometric function

above by a Taylor series in powers of θ −

θ to relate K

to K

trig.

(θ)=K



−sin

θ (θ −

θ) −

cos

(θ −

θ)

+ ···



=⇒

≈ K

sin

θ. (9.15)

The advantage of the trigonometric potential is its boundedness and its ease of

implementation and differentiation. This is because no inverse trigonometric func-

tions need to be calculated, and singularity problems for linear bond angles can

be avoided [1102,1103]. As a compromise between a quadratic and inﬁnite series

in θ −

θ, the MMFF force ﬁeld uses a cubic bond-angle function of form [497]

cubic

= K

(θ −

θ)

+ K

(θ −

θ)

(9.16)

for non-colinear atom orientations. For linear (or near linear) reference angles, the

function

trig.



= K

(1 + cos θ) (9.17)

is used instead.

Note that, as for the bond potential, it is hazardous to use a function that ends

in an odd power of the deformation since these terms have negative coefﬁcients,

which dominate for large deviations. Hence, potential functions that end in even

powers are preferable.

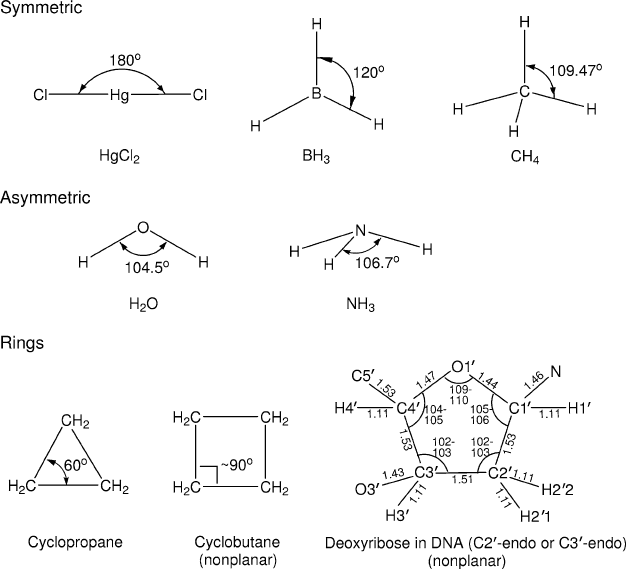
278 9. Force Fields

Figure 9.5. Bond angle geometries for simple chain and cyclic molecules. Note that

cyclobutane and deoxyribose are nonplanar. The former has bond angles less than 90

only 1-2

, but the dihedral angle is substantial, around 30

, which relieves the eclipsing of

the hydrogens substantially. The geometry shown for deoxyribose (bond lengths in

Aand

bond angles in degrees) corresponds to observed C3



-endo and C2



-endo conformations in

B-DNA. The ﬁve endocyclic deoxyribose dihedral angles ν

through ν

have values (as

computed from solvated dodecamers in CHARMM) of approximately −24, 38, −38, 24,

and 0 degrees for C2



-endo, and 0, −24, 38,−38, and 24 degrees for the C3



-endo sugar

pucker.

Figure 9.6 displays harmonic bond angle potentials of the forms given in

eqs. (9.13)and(9.14). Note that the harmonic cosine potential is very similar to

the harmonic potential for a small range of ﬂuctuations. It should thus be preferred

in practice if computational time is an issue.

9.4.2 Cross Bond Stretch / Angle Bend Terms

Cross terms are often used in force ﬁelds targeted to small molecular systems

(e.g., MM3, MM4) to model more accurately compensatory trends in related

bond-length and bond-angle values. These cross terms are considered correction

terms to the bond-length and bond-angle potentials.

9.4. Bond Angle Potentials 279

110 115 120 125 130

0.2

0.4

0.6

0.8

1.2

1.4

(bond angle) [deg.]

Bond Angle energy [kcal/mol]

Harmonic

Trig.

Figure 9.6. Harmonic bond-angle potentials of the form (9.13)and(9.14) for an aro-

matic C–C–C bond angle (CA–CA–CA atomic sequence in CHARMM) with parameters

=40kcal/(Mol-rad.

)and

θ = 2.1 rad (120

). The K

force constant for eq. (9.14)is

calculated via eq. (9.15).

For example, a stretch/bend term for a bonded-atom sequence ijk allows bond

lengths i–j and j–k to increase/decrease as θ

ijk

decreases/increases. A bend/bend

potential couples the bending vibrations of the two angles centered on the same

atom appropriately, so the corresponding frequencies can be split apart to match

better the experimental vibrational spectra [30].

These correlations can be modeled via stretch/stretch, bend/bend, and stretch/

bend potentials for such ijk sequences (see Figure 9.7), where the distances r and



are associated with bonds ij and jk,andθ is the ijk bond angle:



(r, r



)=S [r − ¯r][r



−



] , (9.18)

θθ



(θ, θ



)=K [θ −

θ][θ



−



] , (9.19)

rθ

(r, θ)=SK[r − ¯r][θ −

θ] . (9.20)

Through addition, a stretch/bend/stretch term of form

rθr



(r, θ, r



)=K [S(r − ¯r)+S



−



)] [θ −

θ] , (9.21)

can be mimicked, as in the Merck force ﬁeld [497].

A variation of a stretch/bend term, devised to obtain better agreement of cal-

culated with experimental vibrational frequencies for a bonded atom sequence

ijk and associated bond angle θ [301], is a potential known as Urey-Bradley.