Schneider P., Eberly D.H. Geometric Tools for Computer Graphics

Подождите немного. Документ загружается.

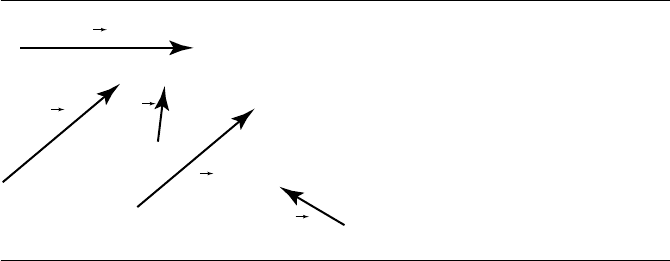
64 Chapter 3 Vector Algebra

Figure 3.1 Vectors as directed line segments.

vectors. However, vectors u and w have the same direction and length, and are thus

equivalent, even though they are drawn at different locations in the ﬁgure. If this

seems to be counterintuitive, think of it this way: if you start off at your house and

walk three kilometers due east, the relative path is the same as if you had started your

trip at your neighbor’s house.

3.1.2 Vector Addition

With this direction-and-distance interpretation in place, we’re now in position to

talk about operations on vectors. First, let’s talk about addition—what does it mean

to add two (or more) vectors? Going back to our “taking a walk” intuitive hook,

this would correspond to walking a particular distance in a particular direction

(one vector) and then immediately walking in some other direction for some dis-

tance. Of course, you could have walked directly to your ﬁnal destination; this

would correspond to yet another vector, which is deﬁned as the sum of the ﬁrst

two.

For example, say we had two vectors u and v, as seen in Figure 3.2, that rep-

resented a two-stage journey. Remembering that the positions of the vectors aren’t

signiﬁcant, we can redraw them as in Figure 3.3. That more direct path from the jour-

ney’s start to its ﬁnish is the sum of the two vectors and can be drawn “head-to-tail”

as shown in Figure 3.4, which makes it more obvious that their sum is the vector w.

This can be mathematically represented as u +v =w.

Because adding two vectors always gives us another vector, we can extend this idea

to “chains” of vector addition, as shown in Figure 3.5, which represents the vector

sum s +



t +u +v =w.

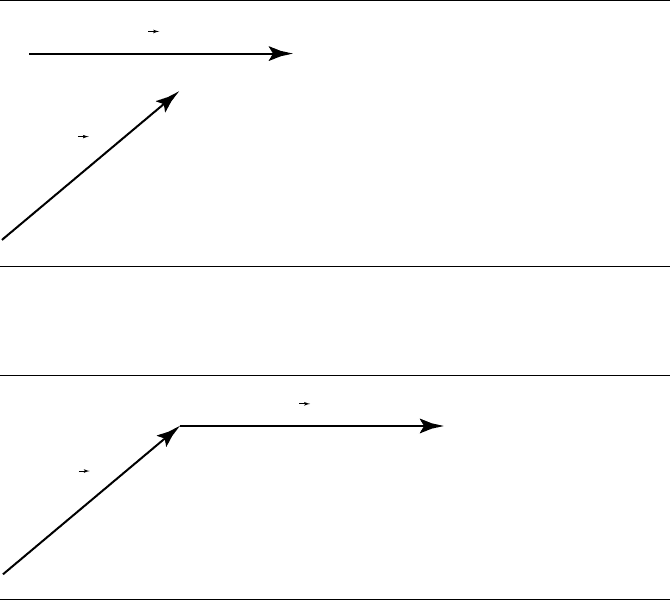
3.1 Vector Basics 65

Figure 3.2 Two ve c to rs .

Figure 3.3 Two vectors drawn head-to-tail.

3.1.3 Vector Subtraction

We can also subtract one vector from another. Intuitively, this is equivalent to taking

a journey of some distance in a particular direction, and then going in the reverse of

some other direction for another distance. This is shown in Figure 3.6.

3.1.4 Vector Scaling

Another fundamental operation on vectors is that of scalar multiplication or scaling.

This simply means changing the length of a vector without changing its direction. In

Figure 3.7 we can see that the vector v has exactly the same orientation as u, but is

twice the length. This is represented mathematically as v =2u.

In general, scalar multiplication is v = α u,whereα is any real number. In the

previous example, we had α = 2, but we could just as easily have a negative α value.

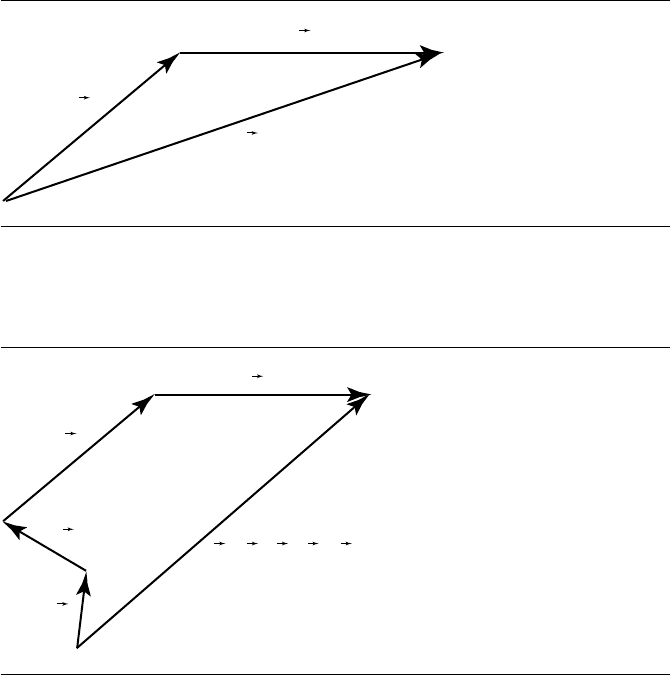
66 Chapter 3 Vector Algebra

Figure 3.4 Vector addition.

w = s + t + u + v

Figure 3.5 Vector addition chain.

Figure 3.8 shows a scaling of u by α =−1 (which can be called, for obvious reasons,

vector negation).

3.1.5 Properties of Vector Addition and Scalar

Multiplication

Now, given these two operations of vector addition and scalar multiplication, you

might wonder if the rules for combining these two operations follow what you know

about ordinary addition and multiplication of simple (i.e., real) numbers.

Let’s look at some of the usual properties:

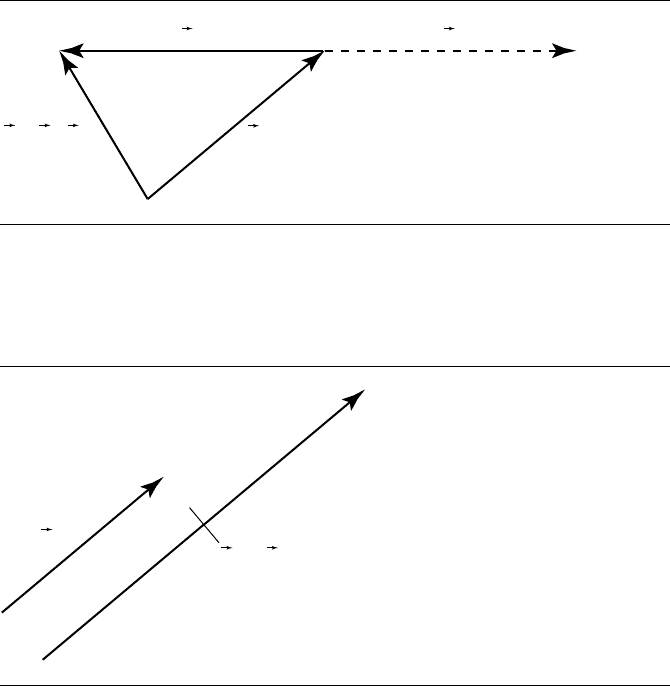
3.1 Vector Basics 67

v–v

w = u – v

Figure 3.6 Vector subtraction.

v = 2u

Figure 3.7 Vector multiplication.

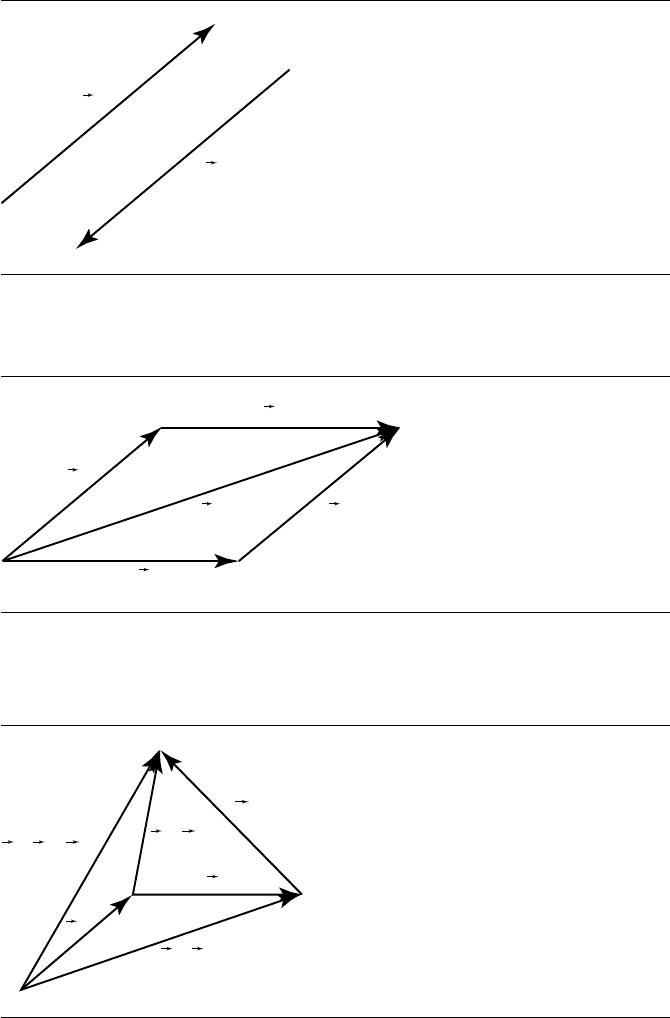
i. Commutativity: u +v =v +u. From Figure 3.9, we can see that the sum is the

same irrespective of the order of the terms.

ii. Associativity: u +(v +w) =(u +v) +w. From Figure 3.10, we can see that the

sum is the same irrespective of the grouping of the terms.

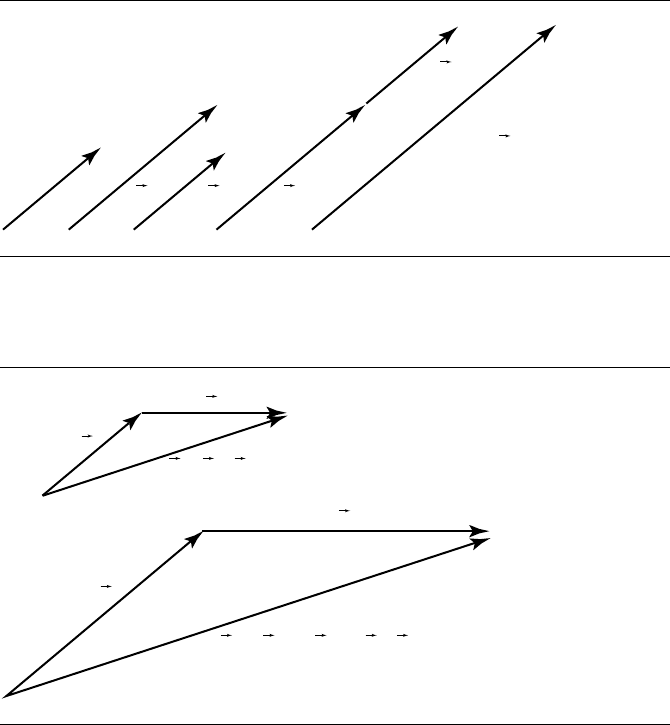
iii. Distributivity of addition over multiplication: (α + β)u = α u + β v. See Fig-

ure 3.11.

iv. Distributivity of multiplication over addition: α(u +v) = α u + α v. From Fig-

ure 3.12, we can see that the sum is the same irrespective of the grouping of the

terms.

68 Chapter 3 Vector Algebra

–u

Figure 3.8 Vector negation.

Figure 3.9 Commutativity of vector addition.

u + v

u + v + w

v + w

Figure 3.10 Associativity of vector addition.

3.2 Vector Space 69

au bu au

(a + b)u

Figure 3.11

Distributivity of addition over multiplication.

w = u + v

aw = au + av = a(u + v)

Figure 3.12 Distributivity of multiplication over addition.

3.2 Vector Space

Although we’ve been talking about vectors as “directed line segments,” the abstract

conceptofavector space can be formalized as follows: a vector space (over real

numbers) consists of a set V , whose elements are called “vectors,” and which has

these properties:

i. Addition (and subtraction) of vectors is deﬁned, and the result of addition or

subtraction is another vector.

70 Chapter 3 Vector Algebra

ii. The set V is closed under linear combinations: if we have u, v ∈V , and α, β ∈R,

then α u + β v ∈ V as well.

iii. There exists a unique vector



0 ∈V , called the zero vector, such that the following

properties hold:

a. ∀v ∈V ,0·v =



0, where 0 ∈ R.

b. ∀v ∈V ,



0 +v =v.

(Note that these all work intuitively for our “directed line segments” version of vec-

tors, except that we haven’t yet talked about multiplication of vectors by vectors. Also,

note that the “closed under linear combinations” includes multiplication of a single

vector by a scalar, which we already discussed.)

3.2.1 Span

Given a set of vectors



v

, v

, ···, v



∈ V , the set S of all linear combinations of

these vectors is an (inﬁnite) set of vectors comprising another vector space, and this

space is called the space spanned by



v

, v

, ···, v



. That is, any vector w ∈ S can

be written as w = λ

v

+ λ

v

+···+λ

v

, for λ

∈ R. The set



v

, v

, ···, v



called the spanning set for S.

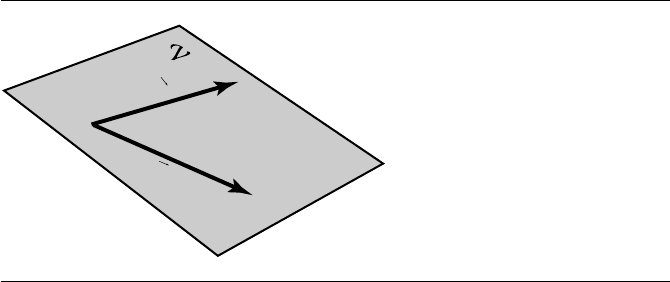
Here’s an example to make this more clear: if we have two (nonparallel) vectors

u and v that are directed line segments existing in three-dimensional space, then

the space spanned by these two vectors consists of all vectors lying within the plane

deﬁned by u and v (see Figure 3.13).

Figure 3.13 The span of two vectors in 3D space is a plane.

3.2 Vector Space 71

3.2.2 Linear Independence

Suppose we have a set of vectors u and v that span some space S. Notice that in the

example diagrammed in Figure 3.13, we stipulated that the vectors u and v must not

be parallel. Intuitively, you can see that if they were parallel, we wouldn’t be deﬁning

a plane with them; we’d be deﬁning a line. Consider the case where we have three

vectors u, v, and w, but with w = α u. We’d still be deﬁning a plane, and the three

vectors would span the same set S. So, either u or w could be considered redundant.

This intuition can be formalized in the deﬁnition of linear independence: the set



v

, v

, ···, v



∈ V is linearly dependent if there exist scalars λ

, λ

, ···, λ

, not all

zero, such that

v

+ λ

v

+···+λ

v



and linearly independent if

v

+ λ

v

+···+λ

v



only if λ

=0, λ

=0, ···, λ

=0. More intuitively speaking, this means that a set of

vectors is linearly independent if and only if no v

is a linear combination of the other

vectors in the set.

3.2.3 Basis, Subspaces, and Dimension

If we have a vector space S,thenaset



v

, v

, ···, v



is a basis for S if



v

, v

, ···, v



are linearly independent

ii.



v

, v

, ···, v



is a spanning set for S

If we have a vector space V , and some set of basis vectors V =



v

, v

, ···, v



∈

V , then the space S spanned by V is called a subspace of V .Thedimension n of S is

deﬁned as the maximum number of linearly independent vectors in S.

To make this more concrete, the example we showed in Figure 3.13 has as the

vector space all directed line segments in three-dimensional space (i.e., V = R

), the

basis vectors are the two directed line segments (i.e., V =



u, v



), and the space S

spanned by V is the plane in which those two vectors lie. The dimension of S is 2.

It is important to note that, for any given subspace S of V , there are inﬁnitely

many spanning sets. Going back to our example, any two nonparallel directed line

segments in the plane constitute a basis for that planar subset of three-dimensional

space.

Suppose we have a set of vectors V =



v

, v

, ···, v



∈ V , which are linearly

independent as described earlier. Any other vector w that is in the space spanned by

72 Chapter 3 Vector Algebra

w = 3u + 2v

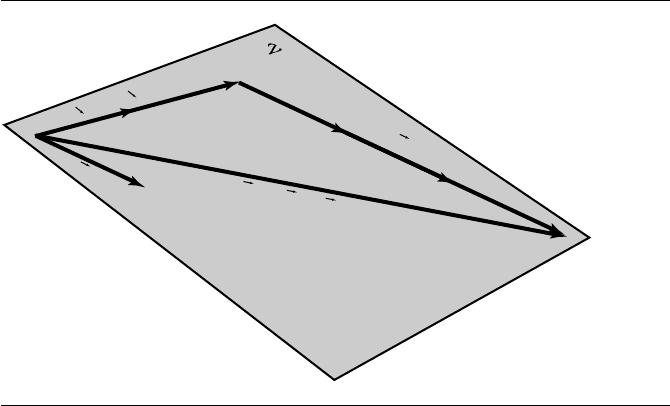
Figure 3.14 A vector as the linear combination of basis vectors.

V can be described as a linear combination of V:

w = x

v

+ x

v

+···+x

v

, x

∈ R

It’s important to note that the factors x

are unique for a given w (otherwise, the

vectors v

would not be linearly independent). We then deﬁne a set of vectors V =



v

, v

, ···, v



∈ V that are linearly independent as forming a basis of (or for) V .

We call the elements x

v

the components of w, and the coefﬁcients x

the coordinates

of w.

An example should make this more clear. Figure 3.14 shows the same two vectors

u and v from Figure 3.13. Because they’re linearly independent (i.e., not parallel and

neither is the



0 vector), they form a basis.

The vector w, which lies in the space V spanned by u and v, can be described

as a linear combination of the basis vectors (speciﬁcally, w =3u + 2v). You can see,

intuitively, that the coefﬁcients (coordinates) of w can only be x

=3, x

=2(“proof

by diagram”); assume that x

is not 3, and note that no possible value of x

could give

you the vector w.

A formal proof of the claim that the linear combination is unique requires that

we state and prove a simpler proposition: Let V =



v

, v

, ···, v



be a basis in V .

Then,



v

= 0 ⇔c

= c

=···=c

= 0.

Proof We need to prove both directions. Let’s do the easy one ﬁrst: if c

=···=c

=0,

then certainly



v

=0 by the deﬁnitions of addition and multiplication. To prove

3.2 Vector Space 73

the other direction, suppose that



v

= 0, and c

= 0 for some j . Then,

v



i=j

−c

v

which contradicts the assumption of linear independence, and therefore c

= c

···=c

= 0.

(This proposition can be stated more intuitively: the zero vector can only be

described as a linear combination of the basis vectors with all the constants equal

to zero, and conversely, if all the constants in a linear combination are zero, the only

thing that it deﬁnes is the zero vector.)

Now, on to the proof that the linear combination is unique. Stated more formally,

let V =



v

, v

, ···, v



be a basis in V .TheneveryvectorinV can be written as a

unique linear combination of v

, v

, ···, v

Proof Suppose we have w ∈V . Then there exist c

, c

, ..., c

∈ R such that

w = c

v

+ c

v

+···+c

v

Suppose that these constants are not unique, that is,

w = d

v

+ d

v

+···+d

v

where some c

= d

. But if that were true, then



0 =(d

− c

)v

+ (d

− c

)v

+···+(d

− c

)v

Recall from the previous proposition that the coefﬁcients of the linear combination

producing the zero vector



0 are all zero; this means that d

= c

, ∀i ∈ 1 ...n. This

proves that every vector w ∈ V can be deﬁned as a unique linear combination of the

basis vectors.

3.2.4 Orientation

Suppose we have two linearly independent vectors u and v. As we have seen, these

can be considered to deﬁne a plane, or if the vectors are three-dimensional, a plane

in 3-space. Figure 3.15 shows these vectors u and v and the angle θ

uv

between them.

Note that we’re “exploiting” some unstated conventions here. We’ve mentioned the

vectors in lexicographic order (u then v) and spoken of the angle between them in that

order (θ

uv

), and the angle arrow in Figure 3.15 goes from u to v, suggesting that the

angle is positive. The angle direction is, in common parlance, “counterclockwise”—it

increases as you go in that standard direction. But, all of these conventions are based

on an assumption that’s so obvious, you’re probably not even thinking about it: all of