Schneider P., Eberly D.H. Geometric Tools for Computer Graphics
Подождите немного. Документ загружается.

94 Chapter 3 Vector Algebra
u
v
w
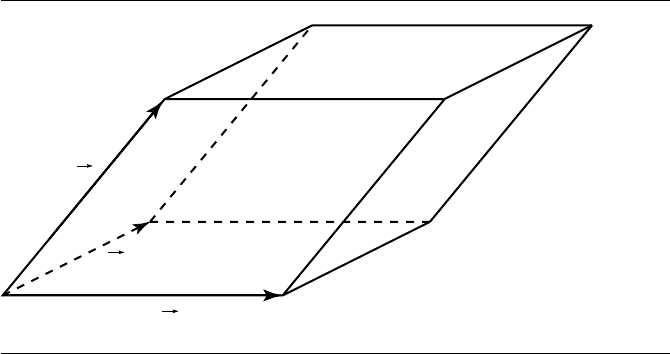
Figure 3.33 Parallelepiped defined by three vectors.
3.3.2 Volume, the Determinant, and the Scalar Triple
Product
It’s natural to assume, because we have operations defining length and area, that we
also can define volume using vector operations. Naturally, the volumetric equivalent
to the parallelogram we used in the cross product is the parallelepiped (Figure 3.33).
First, let’s introduce a notation for volume: if we have a parallelepiped defined by
three linearly independent vectors u, v, and w, its volume is
Vo l
u, v, w
Note that the order of this isn’t significant:
Vo l
u, v, w
= Vo l
v, w, u
=···=Vo l
w, v, u
because they all describe the same parallelepiped.
Now, given we have these three (basis) vectors, how do we determine Vol
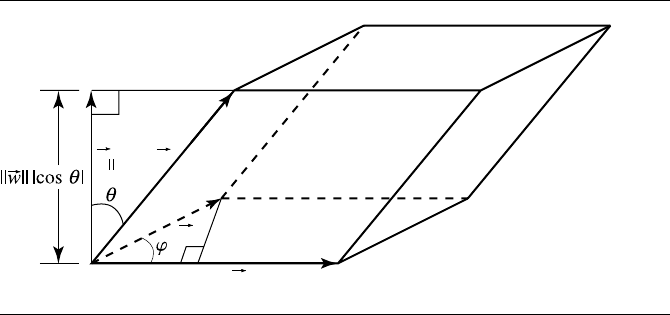
(u, v, w)? Look at Figure 3.34.
Vo l
u, v, w
= base × height by definition
=uv sin ψ ×w
|
cos θ
|
by trigonometry
=uv sin ψ ·w
definition of dot product
=u ×v·w
definition of cross product
=u ×v ·w
definition of length
=u ×v ·w
3.3 Affine Spaces 95
u
v
w
w
Figure 3.34 The scalar triple product.
But, you say, what about orientation? From the above, we can make two obser-
vations:
Vo l
u, v, w
=
u ×v
·w ⇐⇒ w
u ×v
−
u ×v
·w ⇐⇒ w
u ×v
By the right-hand rule,
sgn
u, v, w
= sgn
u, v, w
=
+1 ⇐⇒ w
u ×v
−1 ⇐⇒ w
−u ×v
So, we can conclude that
Vo l
u, v, w
= sgn
u, v, w
u ×v
·w
. (3.12)
The expression
u ×v
·w (3.13)
is commonly referred to as the scalar triple product and is the determinant of a matrix
whose ordered rows (or columns) are u, v, w, which we notate as
det
u, v, w
In the preceding discussion, we separated the sign to emphasize that the determinant
is the signed volume.

96 Chapter 3 Vector Algebra
Note that the definition of the determinant (Equation 3.13) is a subexpression of
Equation 3.12; that is, the determinant is the signed volume:
Vo l
u, v, w
=|det
u, v, w
|=sgn(u, v, w) det
u, v, w
Other properties relating to the determinant, scalar triple product, and volume
are as follows (Goldman 1987):
i. The determinant det(u, v, w) is nonzero if and only if the set {u, v, w} forms a
basis. In three-dimensional space, for example, if three vectors don’t form a basis,
then they must span only a plane or a line, neither of which has volume.
ii. The determinant det(u, v, w) is positive if and only if the sign of {u, v, w) is
positive.
iii. Cyclic permutations of the vectors don’t change their determinant:
det(u, v, w) =det( w, u, v) =det(v, w, u)
iv. Reversing the order of the vectors changes the sign, but not the magnitude of the
determinant:
det(u, v, w) =−det( w, v, u) =−det(v, u, w) =−det(u, w, v)
v. Negating any one of the vectors changes the sign of the determinant:
det(u, v, w) =−det(−u, v, w) =−det(u, −v, w) =−det(u, v, −w)
vi. Scaling the vectors directly scales the determinant:
det(cu, v, w) = det(u, cv, w) = det(u, v, c w) = c det(u, v, w)
vii. The basis vectors of a right-handed orthonormal space have a unit determinant.
3.3.3 Frames
We’re now ready to talk about coordinates with respect to affine spaces. Recall that
an affine space A is defined as a set (space) of points P (a point space)plusan
associated or underlying vector space V , each having the same dimension n.Ifwe
pick an arbitrary point O ∈ P and a basis v
1
, v
2
, ..., v
n
∈V , this forms what we call
a frame
2
for A. We can write this frame as
2. Following DeRose (1989), we eschew the common practice of using the term “space” or “co-
ordinate space” because this use is technically incorrect, or at least, inaccurate and misleading:

3.3 Affine Spaces 97
F =
v
1
, v
2
, ..., v
n
, O
T
Recall that, in a vector space, any vector can be written as a linear combination of
a set of basis vectors (Section 3.2.3). Any u ∈ V can be written as
u = a
1
v
1
+ a
2
v
2
+···+a
n
v
n
The a
1
, a
2
, ..., a
n
are the coordinates of u, relative to the basis v
1
, v
2
, ..., v
n
.
What about the points in P? Here is where the vector and point spaces come
together. Recall that if we have any point P and any vector u, there is a unique point
Q = P +u. If we choose the point O from F as P , then any point Q ∈ P can be
defined in terms of some unique vector u = a
1
v
1
+ a
2
v
2
+···+a
n
v
n
added to O:
Q =u + O
= a
1
v
1
+ a
2
v
2
+···+a
n
v
n
+ O
and so again the coordinates of Q are a
1
, a
2
, ..., a
n
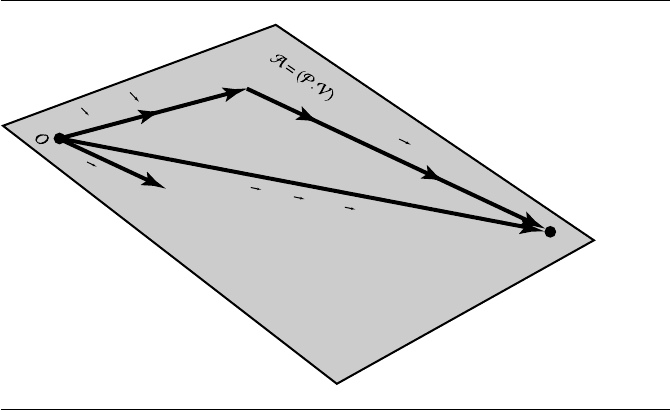
. Figure 3.35 shows an affine space
A =
P.V
with frame F =
v
1
, v
2
, O
T
; the point Q is O +w and has coordinates
(
3, 2
)
.
Cartesian Frames
Note that we’ve now mentioned coordinates, and at least the hint of a relative origin
in the (otherwise arbitrary) choice of O. However, so far all we’ve required for frames
and their underlying basis vectors is that they be linearly independent. Up until
we introduced the dot product, we had no way of formally defining or describing
angles or lengths. We now exploit the angle- and length-defining properties of the
dot product to define a special subclass of Euclidean spaces.
Every vector v has associated with it what’s known as a unit vector, denoted ˆv,
which specifies the same direction as v, but has a length of 1:
ˆv =
v
v
That is, we just scale v by dividing by its own length.
there may be different frames within the same coordinate space, but if you use the common
terminology, you’d have to say that there were different coordinate spaces within the same co-
ordinate space. This sort of statement makes it clear that common usage is overloading the
term “space” with two distinct meanings.
98 Chapter 3 Vector Algebra
v
2
v
1
2v
2
3v
u = 3v
1
+ 2v
2
Q
Figure 3.35 Coordinates of an affine point, relative to an arbitrary frame.
As we can now measure and define angles, we can now ensure that basis vectors
are perpendicular or orthogonal by requiring that v
1
·v
2
= 0. If we have a three-
dimensional space, and the three basis vectors are mutually perpendicular, then it
will also be the case that each vector will be the cross product of the other two (taken
in order—v
1
×v
2
=v
3
, v
2
×v
3
=v
1
, and v
3
×v
1
=v
2
for a right-handed system).
With these tools in hand, we can define a special type of frame for a Euclidean
space—the Cartesian frame—which has basis vectors of unit length, which are mu-
tually perpendicular. Such a basis is also referred to as orthonormal.
3.4 Affine Transformations
An affine transformation is a map taking points and vectors in one affine space to
points and vectors, respectively, in another affine space. In general we say T : A
n
→
B
m
is an affine transformation if it preserves affine combinations:
T
a
1
P
1
+ a
2
P
2
+···+a
n
P
n
= a
1
T
P
1
+ a
2
T
P
2
+···+a
n
T
P
n
(3.14)
with P
i
∈ A and
n
i=1
a
i
= 1. Note that the dimensions n and m need not be the
same, but m ≤ n.
3.4 Affine Transformations 99
T
P
Q
R
T(P)
T(R)
T(Q)
1 – t : t
1– t
: t
Figure 3.36 Affine maps preserve relative ratios.
Because an affine transformation maps points to points, it also maps line seg-
ments to line segments, planes to planes, and so on. We can show this more directly:
Recall that we can write a point R on a line as an affine combination of two other
(noncoincident) points P and Q on the line:
R =
(
1 − α
)
P + αQ
for some α. If we apply the affine map T ,weget
T(R)= T(
(
1 − α
)
P + αQ)
=
(
1 − α
)
T(P)+ αT (Q)
This is very closely related to writing out the equation of a line in parametric form:
R(t) =
(
1 − t
)
P + tQ
to which the map T can be applied:
T(R(t))= T(
(
1 − t
)
P + tQ)
=
(
1 − t
)
T(P)+ tT (Q)
This is just the parametric equation for the line defined by P and Q. Although this is
fairly obvious, it is important to point out that the constants in the above equations
are not affected by the transformation T —t and 1 − t do not change. Put another
way, R has the same relative distances between it and P and Q. Formally, we say that
affine maps preserve relative ratios (see Figure 3.36).
An affine space, as you recall, is a set of points plus a set of vectors. So, naturally
the question arises as to what effect an affine transformation has on vectors. Suppose
100 Chapter 3 Vector Algebra
we have an affine map T that operates on the points of an affine space A. Given two
points P , Q ∈ A, we can take their difference to find a vector
v = Q − P
because this operation defines the relationship between points and vectors in an affine
space. Now, what happens if we apply the affine map? We get
T(v) = T(Q− P)
= T (Q) − T(P)
So, the transformed vector is just the one between the transformed points. Recall,
however, that the vectors that underlie an affine space are elements of a vector space,
and that in a vector space, location of a vector is meaningless. There are infinitely many
other pairs of points in T(A) whose difference is T(v); if you draw a directed line
segment between each of these pairs of points, you just get “copies” of T(v) that have
the same direction and magnitude, but which are merely offset or translated from
one another.
We can go even further than this, though: formally, we say that affine maps
preserve parallelism. To see this, suppose we have two pairs of points {P
1
, P
2
} and
{Q
1
, Q
2
}. Each pair of points defines a line:
L
1
= P
1
+ α(P
2
− P
1
)
L
2
= Q
1
+ β(Q
2
− Q
1
)
These lines are parallel if P
2
− P
1
= γ(Q
2
− Q
1
) (that is, these vectors differ only
in length by a relative ratio of γ and are in the same direction). An affine map then
maps these vectors to scaled versions of the same vector, and so affine maps preserve
parallelism.
We’ll use this observation to characterize affine transformations, in conjunction
with the following: an affine map T is a linear transformation with respect to the
vectors of an affine space A. In Section 3.2.6, we defined a linear transformation as
one that preserves linear combinations. A linear combination of vectors is defined as
w = x
1
v
1
+ x
2
v
2
+···+x
n
v
n
, x
i
∈ R
for a set of linearly independent vectors v
i
∈ V . To say that a linear map preserves
linear combinations requires that
T(w) = T
v
1
x
1
+v
2
x
2
+···+v
n
x
n
(3.15)
= T
v
1
x
1
+ T
v
2
x
2
+···+T
v
n
x
n
(3.16)
= x
1
T
v
1
+ x
2
T
v
2
+···+x
n
T
v
n
(3.17)
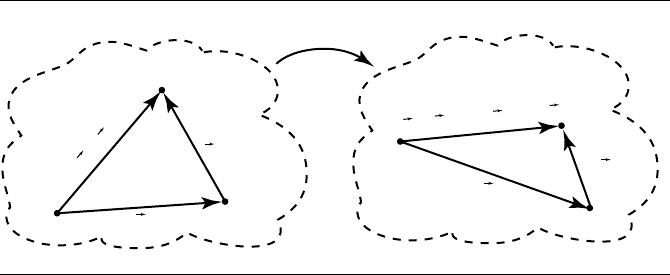
3.4 Affine Transformations 101
P
T(P)
Q
T(Q)
R
T(R)
u
v
T(v)
u + v
T(u)
T(u + v) = T(u) + T(v)
T
Figure 3.37 Vector sum.
∀x
1
, x
2
, ..., x
n
∈R, ∀v
1
, v
2
, ..., v
n
∈V . Equation 3.15 above was broken down into
Equations 3.16 and 3.17 separately in order to show the two aspects to preservation
of linear combinations, and accordingly, we must show that both conditions hold.
We can do this for a two-dimensional affine space and extend it to higher dimensions
by induction on the number of basis vectors. First, we have to show
T(u +v) = T(u) + T(v) (3.18)
Suppose we have two vectors u and v, as shown in Figure 3.37. The proof is trivial:
T(u +v) = T(R− P)
= T(R)+ (T (Q) − T (Q)) − T(P)
= (T (R) − T (Q)) + (T (Q) − T(P))
= T(v) + T(u)
= T(u) + T(v)
We must also show now that
T(αv) = αT (v)
As shown in Figure 3.38, we can rewrite αv as ((1 − α)P + αQ) − P . If the “proof
by diagram” isn’t sufficient, consider the following:
T(αv) = T (((1 − α)P + αQ) − P) by substitution
= T((1 − α)P +αQ) − T(P) by Equation 3.18
= (1 − α)T (P ) + αT (Q) − T(P) by Equation 3.18
= αT (v) by definition of affine combination
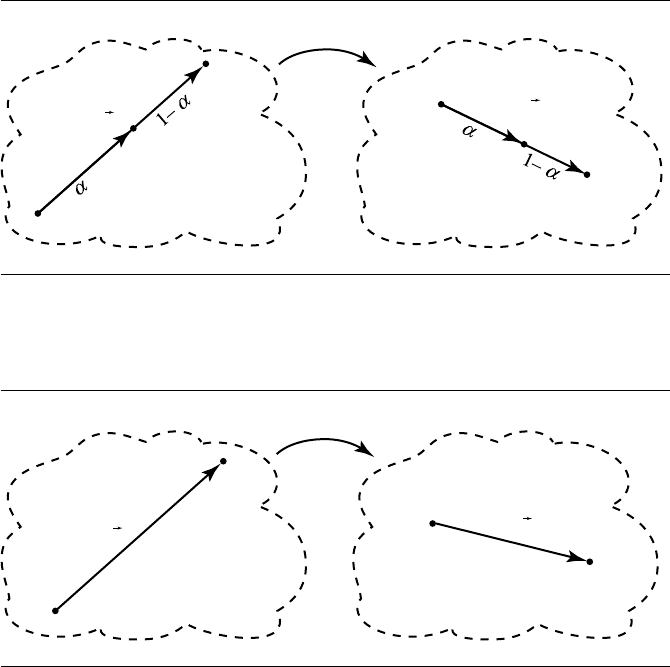
102 Chapter 3 Vector Algebra
P
T(P)
Q
T(Q)
v
T(v)
R
R
T
Figure 3.38 Vector scale.
P
T(P)
Q
T(Q)
v
T(v)
T
Figure 3.39 Sum of point and vector.
Finally, an affine map also preserves addition of vectors to points:
T(P +v) = T(P)+ T(v)
Referring to Figure 3.39, we can see the usual definition of a point as the sum of
a point and a vector: Q = P +v,orv = Q − P . This leads to the following proof
(DeRose 1992):
T(P +v) = T(P + (Q − P)) by definition of subtraction of points
= T(P)+ T (Q) − T(P) by definition of transformation
= T(P)+ (T (Q) − T(P)) by associativity of vector addition
= T(P)+ T(v) by definition of subtraction of points

3.4 Affine Transformations 103
Together, these properties show that an affine transformation T preserves affine
coordinates:
T
α
1
v
1
+ α
2
v
2
+···+α
n
v
n
+ O
=α
1
T(v
1
) + α
2
T(v
2
) +···+α
n
T(v
n
) + T(O)
The above was written as a general statement, but notice that the notation is that of
an affine frame. So, an affine transformation is completely and uniquely defined by
its action on a frame, or on a simplex.
3.4.1 Types of Affine Maps
As shown in the previous section, an affine map’s operation on the vectors of an affine
space A is that of a linear map; this allows for rotations and scales (both uniform and
nonuniform). Because vectors (even those of A.V) carry no positional information,
this excludes any operation that is related to position (such as translation).
As affine maps operate on both A.P and A.V, mapping points to points and so
on, they are able to represent transformations involving relative positions:
Translations
Mirror or reflection about an arbitrary line or plane
Parallel projection
Rotation about an arbitrary point
Shearing relative to arbitrary lines or planes
These transformations will be covered in more detail in Section 4.7.
3.4.2 Composition of Affine Maps
In Section 2.7.1, we discussed maps in a general sense, and how you can compose
maps by using the output (the range) of a function T as the domain of another
function U . Affine maps, of course, are no different in this regard; we can build up a
complex series of transformations by simply applying one affine map after another.
The characteristics of affine maps, as described in the previous sections, ensure that
we never leave affine space, and thus we can consider the composition of any number
of affine maps to be just another single affine map, albeit a more complex one. A
rather obvious example of this is a series of rotations (about the same point) of α, β,
and γ degrees; clearly this is the same as a single rotation of α +β +γ (Figure 3.40).
