Schneider P., Eberly D.H. Geometric Tools for Computer Graphics
Подождите немного. Документ загружается.


84 Chapter 3 Vector Algebra
This form is generally used when the term affine combination is used and is quite a
convenient notation.
It should be clear that if we set α between 0 and 1, the point R will be between
P and Q; if this is the case, then we call this a convex combination. However, our
definition of affine combination doesn’t really preclude us from setting α outside this
range, in which case the resulting R will be somewhere on the (infinite) line defined
by P and Q.
We can extend the affine combination, as you may have suspected, to involve
more than just two points: Given n points P
1
, P
2
, ..., P
n
, and n real numbers
α
1
, α
2
, ..., α
n
whose sum is 1, we can define an affine combination to be
P
1
+ α
2
P
2
− P
1
+ α
3
P
3
− P
2
+···+α
n
P
n
− P
1
and again rewrite this as
α
1
P
1
+ α
2
P
2
+···+α
n
P
n
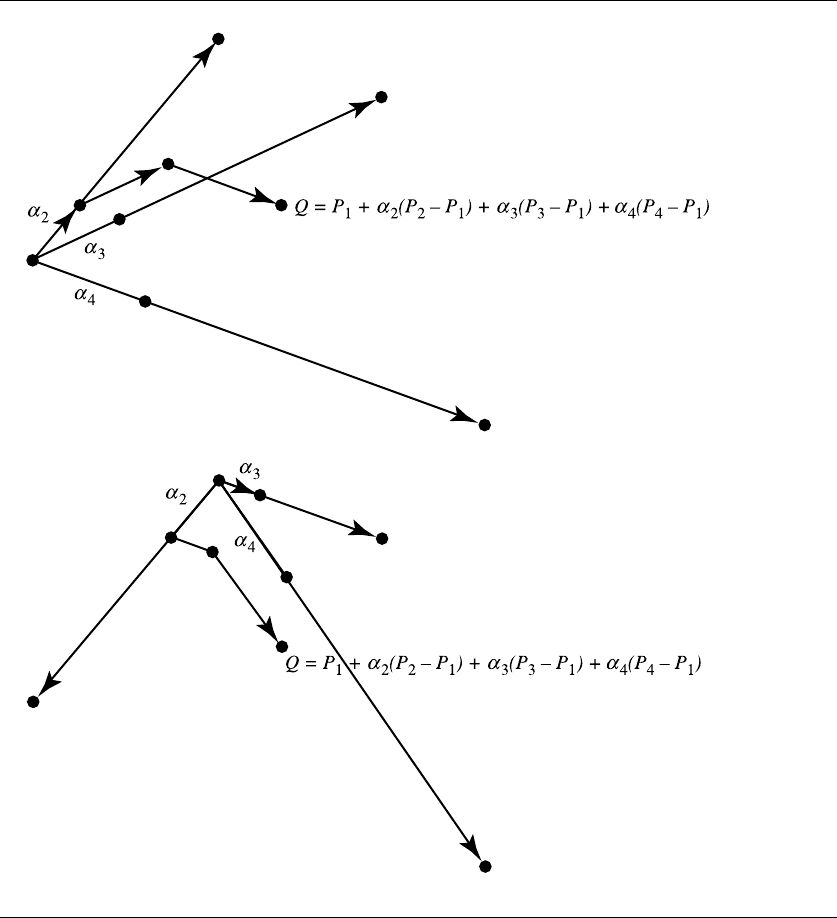
An example is shown in the top of Figure 3.26, in which α
1
=α
2
=α
3
=α
4
=0.25.
The careful reader may have noticed that α
1
does not appear in the original affine
combination, yet it does appear in the rewritten form below it. Why are P
1
and
α
1
“special”? Actually, they are not. We can interchange the roles of P
1
and any of
the other points, compute the affine combination using the same coefficients, and
produce the same point. The lower diagram in Figure 3.26 shows what happens when
we interchange P
1
and P
2
—we get the same Q as an affine combination.
3.3.1 Euclidean Geometry
You should have noticed several things missing from all of these discussions of affine
geometry:
There has been no mention of any concept of an origin in an affine space.
We’ve only really talked about angle in a rather general sense, but not specified
how we define or compute angles.
While it’s clear that two points in affine space are separated by some distance,
we’ve not discussed it beyond that.
These have not been accidental omissions. In fact, affine space by definition has no
origin (there is no special point distinct from all others) and does not include any
mechanism for defining length or angle (remember, affine space itself consists of
points, and thus the questions “What is the angle between two points?” and “What is
the length of a point?” are meaningless).
The lack of a predefined origin to an affine space shouldn’t really bother us,
though: typically, in computer graphics and geometric design, models (in the sense of
3.3 Affine Spaces 85
P
2
P
3
P
4
P
3
P
1
P
1
P
4
P
2
Figure 3.26 Affine combination of several points.

86 Chapter 3 Vector Algebra
v
v
v
u
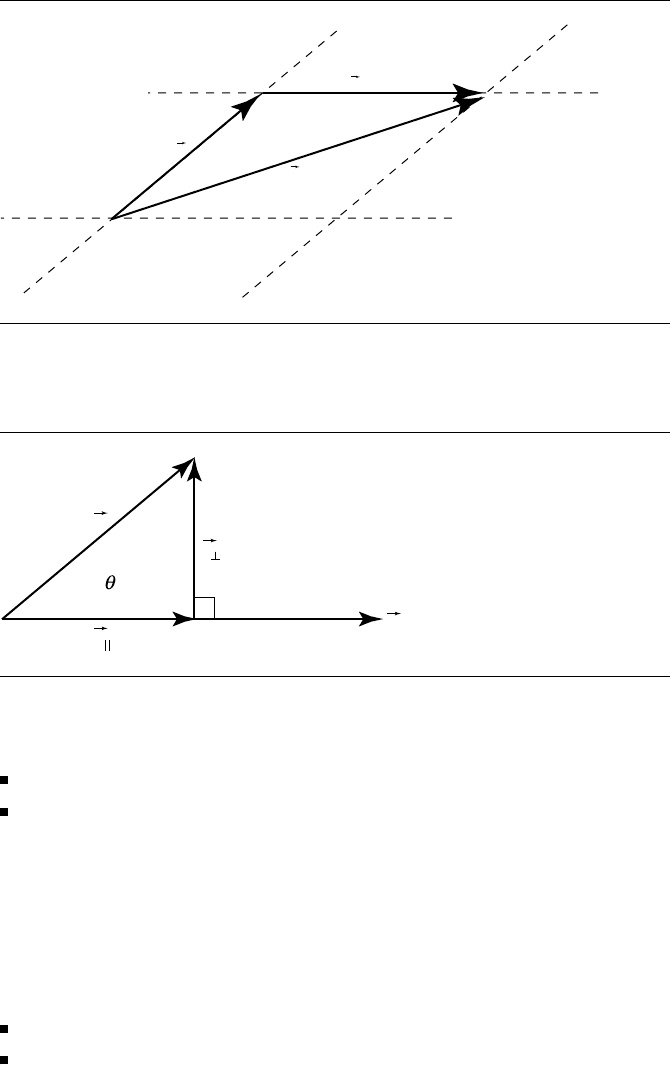
Figure 3.27 Angle between vectors and vector length.
cars, etc. or virtual worlds) are defined by hierarchies of components, each of which
is created in its own space, and then its space is located inside the “next higher level’s”
space, and so no point really is distinguished—only the relative relationships between
points matter. We’ll get to the problem of origins of spaces in a later section.
For now, let’s concentrate on length, distance, and angle. These aren’t omitted
from affine space because they’re not useful concepts—of course they’re essential. It’s
just that these properties are properly part of what’s called Euclidean space, which
can be considered to be affine space with the addition of this “metric” information.
Euclidean space can then be considered a specialization of, or a subset of, affine
space; all of the principles and properties we’ve discussed about affine space apply
to Euclidean space, plus these new metric properties.
We’ve seen how to add and subtract vectors, and how to multiply them by scalars,
and also how these two sorts of operations interact. There are two other fundamental
vector operations, both of which are forms of multiplying two vectors together; these
are the scalar product, so called because it produces a single-valued (i.e., scalar) result,
and the vector product, so called because it produces another vector.
The scalar product is related to the questions “What is the angle between two
vectors?” and “What is the length of a vector?” (Figure 3.27), while the vector product
is related to the area of the parallelogram formed by two vectors placed tail-to-tail, as
when we diagram the additive operation (Figure 3.28).
Scalar Product
The scalar product is commonly known as the dot product, a special case of an inner
product. Before continuing, there are a few symbols we need to define:
Length: The length of a vector u is written as u.
Direction: The direction of a vector u is written as dir(u).
Sign: The sign of a scalar is written as sgn(α).
3.3 Affine Spaces 87
u
v
w
Figure 3.28 Parallelogram rule for vector addition.
v
u
v
v
Figure 3.29 Vector projection.
Perpendicular: A vector u perpendicular to a vector v is written as u ⊥v.
Parallel: A vector u parallel to a vector v is written as u v.
Before discussing the scalar product, we need to step back a little and discuss pro-
jection of vectors, in order to provide some intuition as to why the scalar product is
useful and why it is so defined.
Suppose we have two vectors u and v and draw them as shown in Figure 3.29,
so that the angle between them is θ.Thevectorv can be decomposed into two
components relative to u:
v
⊥
(perpendicular to u)
v
(parallel to u)

88 Chapter 3 Vector Algebra
Note also that v
+v
⊥
=v. By convention v
⊥
is called the normal component of v
with respect to u, and v
is called the orthogonal projection of v on u (“orthogonal”
because it’s projected in a direction perpendicular to u).
What we’re interested in here are the relationships between v
, v
⊥
, and the angle
θ. First let’s apply a little trigonometry and look at the lengths of v
⊥
and v
, and
observe that (by definition of sine and cosine, respectively)
v
⊥
=v| sin θ| (3.2)
and
v
=v| cos θ | (3.3)
Now, what about the vectors themselves? This takes a bit more explanation than
just appealing to the definitions of fundamental trigonometric relationships. The first
claim is that
v
=v cos θ ˆu
where ˆu =
u
u
is a unit (length = 1) vector having the same direction as u. That is, v
is obtained by scaling u by the ratio of the length of v to u multiplied by the cosine of
the angle between them. To show that this is the case, we have to show that these two
vectors (v
and
v
u
cos θ u) are the same; we have to show that they have the same
direction and length. Taking length first:
v
=v cos θ ˆu
v
=v
|
cos θ
|
ˆu
but ˆu=1 because it is by definition a unit vector, so we have
v
=v
|
cos θ
|
which proves the vectors have the same length.
To show equivalent direction, we have to consider two cases:
i. cos θ is positive (as in Figure 3.29).
ii. cos θ is negative (as in Figure 3.30).
In the former
dir
v cos θ ˆu
= dir
ˆu
⇐⇒ cos θ>0
dir
v cos θ ˆu
=−dir
ˆu
⇐⇒ cos θ<0

3.3 Affine Spaces 89
v
u
v
v
Figure 3.30 cos θ negative.
So for cos θ<0 and cos θ>0, we have
dir
v cos θ ˆu
= dir
v
(3.4)
Note that if cos θ = 0(θ = 90
◦
or θ = 270
◦
), both v cos θ ˆu and v
become the
0
vector, and the relationship still holds.
To show that v
⊥
=v
|
sin θ
|
, we can simply note that
v =v
⊥
+v
which we can rearrange as
v
⊥
=v −v
and the desired result follows directly.
So, we have in the orthogonal projection (v
) an entity that is related to the angle
θ between two vectors.
1
If you look at the relations we just proved, and the figures that
go with them, you’ll notice that the length and direction of v, and the direction of u,
affect the length and direction of v
, but the length of u has no effect! Furthermore, v
is a vector, and it would be preferable to have a scalar—a single value—to characterize
the angle while simultaneously taking into account the lengths of the two vectors.
The foregoing is the long way around to justifying the otherwise seemingly arbi-
trary definition of the dot (scalar) product of two vectors; formally, the dot product
is defined as follows: if u and v are vectors and θ is the angle between u and v, then
the dot product u ·v is defined by
1. We can just arbitrarily focus on v
because if we know v and v
, v
⊥
can be computed with a
simple vector subtraction.

90 Chapter 3 Vector Algebra
u ·v =
uv cos θ ,ifu =
0 and v =
0
0, if u =
0orv =
0
(3.5)
which of course implies that, for nonzero vectors u and v,
cos θ =
u ·v
uv
(3.6)
and
θ = cos
−1
u ·v
uv
(3.7)
The dot product has a number of important properties:
i. Definition: u ·v =uv cos θ .
ii. Bilinearity: ∀α, β ∈R, and ∀u, v, w ∈A.V ,
a.
α u + β v
·w =α
u ·w
+ β
v ·w
.
b. u ·
αv +β w
= α
u ·v
+ β
u ·w
.
iii. Positive definiteness:
a. ∀u ∈ A.V , u =
0, u ·u>0.
b.
0 ·
0 =0.
iv. Commutativity: u ·v =v ·u.
Proof
u ·v =uvcos θ
=uv cos(−θ)
=v ·u
v. Distributivity of the dot product over vector addition: u ·
v +w
=
u ·v
+
u ·w
First, we must prove a simple relationship: u ·v
=u ·v. The angle α
between v
and u is either 0
◦
or 180
◦
, depending on whether θ is less than 90
◦
.
So, cos(α) is either 1 or −1, respectively; this may be restated as saying that
cos(α) = sgn(cos θ). Thus, we have
u ·v
=|u||v
| cos α (3.8)
=|u||v|| cos θ | sgn(cos θ) (3.9)
=|u||v| cos θ (3.10)
=u ·v (3.11)

3.3 Affine Spaces 91
Proof Let γ be the angle between v
+w
and u. By Equation 3.8, we have
u ·
v +w
=u ·
v +w
=u ·
v
+w
=uv
+w
cos γ
There are now two cases:
a. Parallel: u
v
u ·
v +w
=uv
+w
cos γ
=u
v
+w
cos γ
=u ·v
+u ·w
=u ·v +u ·w
b. Nonparallel: u
|| v
u · (v +w) =uv
+w
cos γ
=u(v
−w
)
=uv
−u w
=u ·v
+u ·w
=u ·v +u ·w
vi. Distributivity of vector addition over the dot product: (u +v) ·w =u ·w +v ·w.
Proof
(u +v) ·w =w · (u +v) by commutativity
=w ·u +w ·v by distributivity
=u ·w +v ·w by commutativity
So we have
i. Squared length: u ·u =u
2
ii. Angle: θ = cos
−1
u·v
uv
iii. Projection: v
=
(
u·v
)
u
u·u
92 Chapter 3 Vector Algebra
v
u
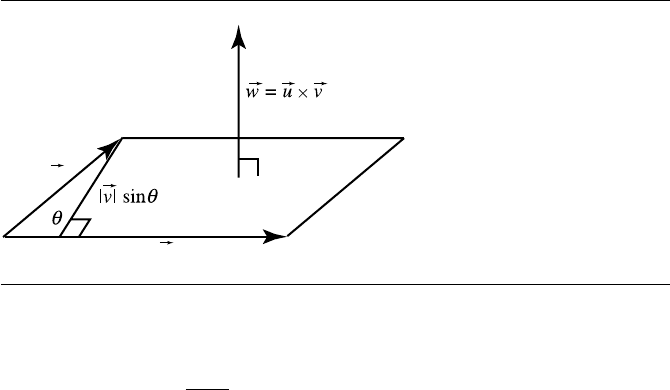
Figure 3.31 The vector product.
iv. Normal: v
⊥
=u −
(
u·v
)
u
u·u
v. Perpendicular: u ·v =0 ⇐⇒ u ⊥v
In the discussion of affine combinations earlier in this section, we explained a
“notational abuse,” in which we allowed ourselves to multiply a point by a scalar. In
the case of dot products, we also will occasionally abuse the notation and allow our-
selves to take the dot product of a vector with a point. For example, in Section 5.1.1,
we describe the implicit form of a line as n ·X =d. Of course, dot products involving
points are not strictly “legal”; however, as with the case of the affine combinations,
we’ll define our way out of the problem by just stating the following: wherever an ex-
pression like n ·X appears, what we really mean is n ·(X − O),whereO is the origin
of the affine frame.
Vector Product
The other vector multiplication operation, the vector product, is also known as the
cross product. The scalar product was discussed in an n-dimensional setting, but here,
we restrict the discussion of the cross product to three dimensions; the extension of
cross products to higher dimensions only works for some dimensions. Like the dot
product, the cross product is related to the angle between two vectors, but can also
be understood as defining the area of the parallelogram formed by two vectors placed
tail-to-tail (see Figure 3.31).
Another useful way of motivating the idea of the cross product is this: if we
have two (nonparallel) vectors u and v, we can consider them to define a (two-
dimensional) plane. If you think about this plane as “floating about in space,” rather
than “on the page,” then the dot product can help us find the angle between the
vectors, but says nothing about the orientation of the plane in space.
3.3 Affine Spaces 93
v
u
Out of page Into page
v
u
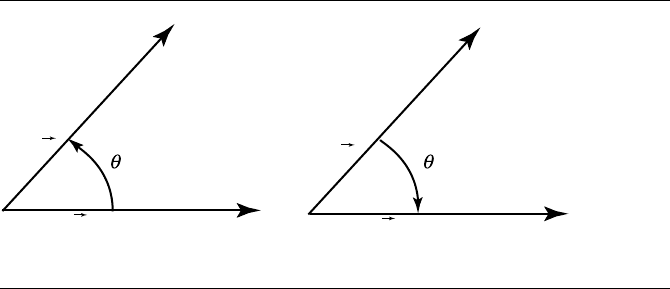
Figure 3.32 The right-hand rule.
We can go about defining the cross product of two vectors u and v as another
vector w that is perpendicular to the plane containing u and v, and whose length is
related to the angle between these two vectors. We use the × symbol to indicate the
cross product. The defining properties are the following:
i. The cross product of two vectors w =u ×v isavector.
ii. The cross product of two vectors is perpendicular to those two vectors:
dir(u ×v) ⊥u, v
iii. The length of the cross product of two vectors is equal to the area of the parallel-
ogram formed by u and v: u ×v=Area
u, v
=uv sin θ
Note that if θ>0, the area is positive, and if θ<0, then the area is negative; if the
unsigned area is desired, then the absolute value of sin θ should be used instead.
The astute reader may have noted that there are two vectors perpendicular to
the plane defined by u and v—one points “outward” or “up,” and the other is its
opposite, pointing “inward” or “down.” By convention, we use the right-hand rule we
introduced earlier: if the angle θ between u and v is positive, then the cross product
vector points “out of the page,” and conversely if θ is negative (see Figure 3.32).
Other properties of the vector product:
i. Anticommutativity: u ×v =v ×u.
ii. Distributivity: u ×
v +w
=
u ×v
+
u ×w
.
iii. Distributivity:
α u
×v =u ×
αv
= α
u ×v
.
iv. Parallelism: u v ⇐⇒ u ×v =
0.
