Schneider P., Eberly D.H. Geometric Tools for Computer Graphics

Подождите немного. Документ загружается.

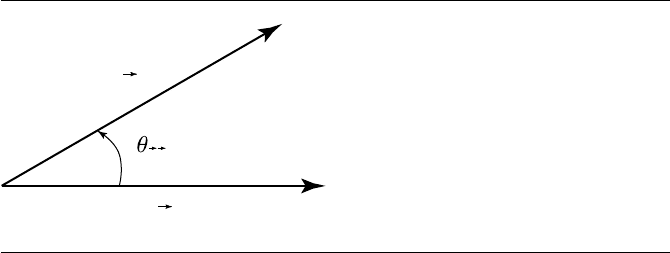
74 Chapter 3 Vector Algebra

Figure 3.15 Angle between vectors.

these drawings are done on a page, which has a built-in third dimension, but which

also has a well-deﬁned third direction—that being what “out of the page” means (the

page has thickness, the ink on the diagram is on one of the surfaces, and we consider

that surface to be the “front” as opposed to the “back,” and so counterclockwise is

well deﬁned).

What if we look at Figure 3.15 as what it really deﬁnes—an inﬁnitely thin plane—

and look at it from the other side? Then, our notion of “in” or “out” of the page

reverses the sense of what’s counterclockwise (i.e., the orientation). So, in reality

we can’t distinguish the orientation. We’ve just been “cheating” by exploiting well-

established conventions for printing diagrams on a page, in particular the idea of

“out of the page” as opposed to “into the page.” That last observation suggests that

it’s really this idea of a third direction that allows us to deﬁne orientation and gives

us a way out of the ambiguity.

Now, suppose we have, in addition to the basis vectors u and v, a third (linearly

independent) vector w; we can think of w as giving us that “out of the page” direction.

Of course, v can serve the same role with respect to u and w, and so on. This (ﬁnally)

allows us to deﬁne the orientation, or sign, for a basis as follows:

sgn



u, v, w



= sgn



uv



If we refer back to Figure 3.15, we’d have w pointing in or out of the page, depending

on how we chose our convention. It seems a bit more “natural” to choose w to be

out of the page, as that corresponds to our idea of a front and back of a sheet of

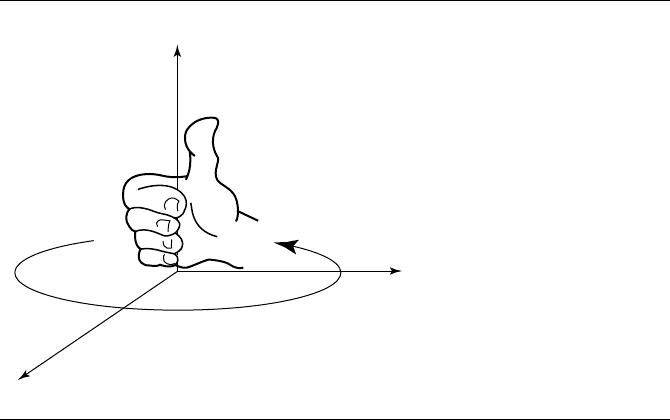
paper. This convention is known as the “right-hand rule” because if we take our

right hand and curl our ﬁngers in the direction of positive rotation, that orientation-

deﬁning direction corresponds to the direction our thumb is pointing, as shown in

Figure 3.16. If the sign of a basis is positive, we use the notation

sgn



u, v, w



=+1

3.2 Vector Space 75

Figure 3.16 The right-hand rule for orientation.

3.2.5 Change of Basis

We just showed that every vector in a particular space is a unique linear combination

of a particular set of basis vectors. However, this doesn’t mean that every vector

has a unique linear combination representation. For any given vector space V of

dimension n, there are an inﬁnite number of linearly independent n-ary subsets of

V . That is, any vector w ∈ V can be represented as a linear combination of any

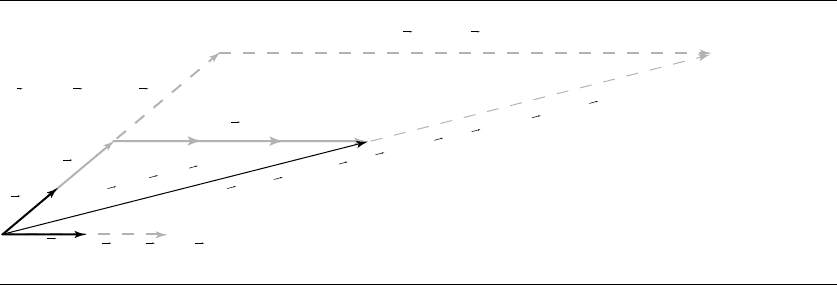
arbitrarily chosen set of basis vectors. The vector w = 3u +2v in Figure 3.14 can also

be represented as w =3s +



t, as shown in Figure 3.17.

How this can be true is fairly obvious, intuitively. A formal explanation of how

this works might be useful: Suppose we have two sets of basis vectors a

, a

, ..., a

and



, ...,



for V . We know that any vector in V can be represented in terms

of any basis, and of course this is true for vectors that themselves make up another set

of basis vectors. That is, each of the a’s can be represented in the basis formed by the



b’s:

a

= c

1,k



+ c

2,k



+···+c

n,k



(3.1)

If we have a vector w ∈ V , we can represent it as a linear combination of

a

, a

, ..., a

and substitute the a

equations (3.1) in that combination to obtain

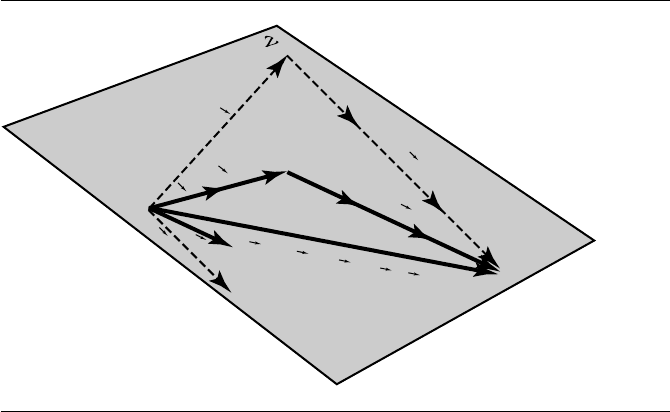
76 Chapter 3 Vector Algebra

w = 3u + 2v = 3s + t

Figure 3.17 A vector as the linear combination of two different sets of basis vectors.

w = d

a

+ d

a

+···+d

a

= d

1,1



+ c

2,1



+···+c

n,1



)

+ d

1,2



+ c

2,2



+···+c

n,2



)

+···+d

1,n



+ c

2,n



+···+c

n,n



)

= (d

1,1

+ d

1,2

+···+d

1,n

)



+ (d

2,1

+ d

2,2

+···+d

2,n

)



+···+(d

n,1

+ d

n,2

+···+d

n,n

)



We’ll see in the next chapter that this laborious-looking computation can be accom-

plished trivially by using matrix multiplication.

3.2.6 Linear Transformations

Before we delve into this directly, let’s review a little precalculus. If we have two sets

D and R, we can deﬁne an operation that associates each element in D with exactly

one element in R. If we apply this operation to all elements of D, then we can

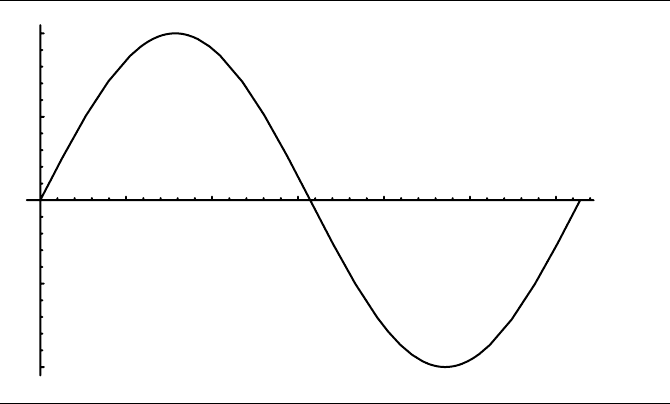
3.2 Vector Space 77

1 2 3 4 5 6

–1

–0.5

0.5

Figure 3.18 The sine function.

view the results as a set of pairs of elements

(

a, b

)

, a ∈ D, b ∈ R. Formally, we call

this operation of associating elements of the two sets a function, transformation,or

mapping (all of which are equivalent and interchangeable terms); the set D is known

as the domain, and the set R is known as the range of the function. It is important

to note that either or both the domain and range may be inﬁnite or ﬁnite. Further,

the function may be continuous or discontinuous. Many values in the range may be

mapped to the same value in the range, but each value in the domain may be mapped

to only one value in the range.

Frequently, a function is depicted as some sort of a graph, with the domain along

the horizontal axis, the range along the vertical axis, and the values of the function

shown as a line or curve, or as bars. Formally the set {(x, f(x)): x ∈ D}⊂D × R

is deﬁned to be the graph of a function. A canonical example of a function is the

trigonometric function sine. The domain consists of all real numbers; the range is

all real numbers between −1 and 1 (see Figure 3.18).

What we’re interested in talking about here are what we call linear transforma-

tions, which are mappings from one linear (vector) space to another. Formally, a

linear transformation between two vector spaces U and V is a map T : U → V

such that

i. T



u +v



= T



u



+ T(v) for any vectors u, v ∈V

ii. T



α u



= αT



u



for any α ∈ R and any u ∈ V

Frequently, a linear transformation is said to preserve linear combinations. Recall

that a linear combination of vectors is deﬁned as x

v

+ x

v

+···+x

v

, x

∈ R,

78 Chapter 3 Vector Algebra

2T(u) = 2(3u)

s = 2T(v) = 2(2v)

r =T(u) = 2u

w = 3u + 2v

t = T(w) = T(3u + 2v) = 2(3u + 2v) = 2(3u) + 2(2v)

Figure 3.19 Linear transformation “scale by two.”

which can be decomposed into the two operations speciﬁed above, and you can see

how these are equivalent requirements. Linear transformations always map lines to

lines (or to zero), and it is always the case that T(



0) =



0. Figure 3.19 should give you

an intuition for this. In this case, the transformation is “scale by a factor of two.” You

can see directly that the linear combination is preserved:



t = T



w



= 2



3u + 2v



= 2



3u



+ 2



2v



Because linear transformations preserve linear combinations, and all vectors u

∈

V can be written as a linear combination of some set of basis vectors {v

, v

, ..., v

a linear transformation can be characterized by what it does to the basis vectors.

We can understand what sorts of operations linear transformations can perform by

considering what transformations we can perform on a vector: changing its length

(scaling) or direction (rotation). The transformation shown in Figure 3.19 was a

uniform scaling, as the basis vectors were both scaled by the same value; however, it is

certainly permissible to scale each vector by a different value, in which case we get a

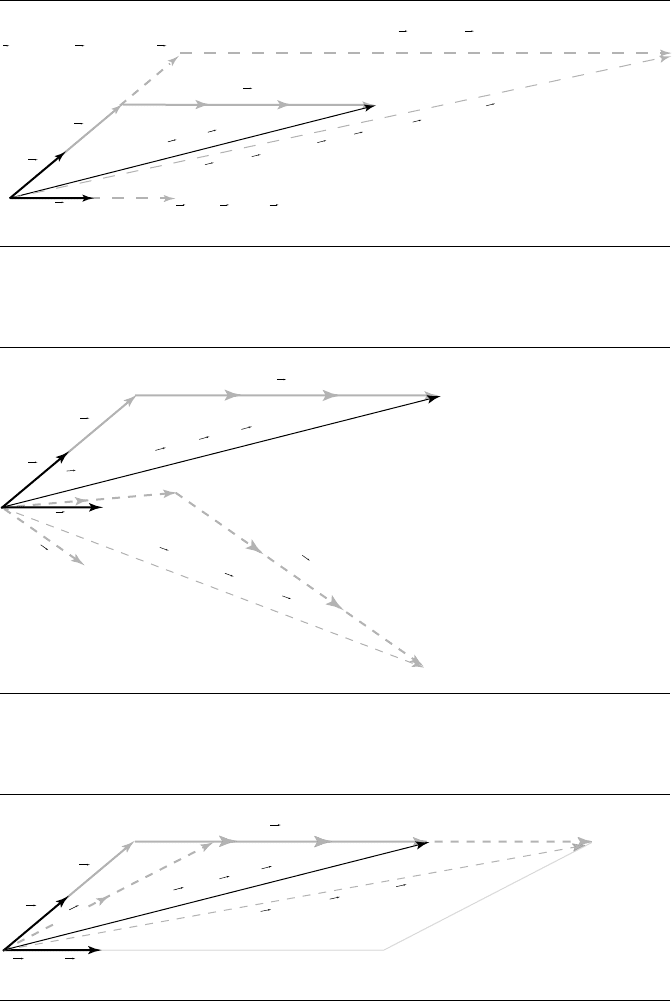
nonuniform scaling (Figure 3.20 shows the results of scaling one basis vector by 2 and

the other by 1.5). If we rotate the basis vectors in the same way, we effect a rotation

(by the same amount) in all vectors that are linear combinations of those basis vectors

(Figure 3.21). Finally, a shear transform scales only one component of a basis vector

(Figure 3.22).

3.2 Vector Space 79

2T(u) = 2(3u)

s = 1.5T(v) = 1.5(2v)

r =T(u) = 2u

w = 3u + 2v

t = T(w) = T(3u + 2v) = 2(3u) + 1.5(2v)

Figure 3.20 Nonuniform scale linear transformation.

w = 3u + 2v

3T(u)

T(w) = 3T(u)+ 2T(v)

T(u)

T(v)

Figure 3.21 Rotation transformation.

w = 3u + 2v

T(w) = 3T(u) + 2T(v)

u = T(u)

T(v)

Figure 3.22 Shear transformation.

80 Chapter 3 Vector Algebra

3.3 Afﬁne Spaces

So far, all we’ve talked about are vectors—what they are, what you can do with them,

and so on. But what about points? The world can be viewed as a space of points

(locations). How can we relate these points to the vectors we’ve been talking about?

The rather obvious intuition is that if we have a point, we can “attach” a vector to it,

and at the end of that vector we have another point. Further, if we have two points,

there is a vector pointing from one to the other, and vice versa.

So, we have this clear functional distinction between points and vectors. In order

to make it very clear which we’re talking about, we’ve adopted a common convention

for our notation: a vector always appears with either a diacritical arrow over it (u, v)

ora“hat”(ˆu, ˆv) in the case of unit-length vectors and is generally lowercase; points

are written without the arrow and are uppercase (P , Q). Since we can have a vector

between two points, occasionally we’ll use a notation that makes this explicit— pq is

avectorfromP to Q.

Formally, an afﬁne space A consists of a set of points P and a set of vectors V ,

which are a vector space spanned by some basis or bases of V . The dimension n of A

is the dimension of V . We refer to the points in A as A.P and the vectors as A.V .

The relationship between the point space and underlying vector space of an afﬁne

space was intuitively explained above. More formally, the relationship is determined

by the axioms deﬁning subtraction of pairs of points and the so-called Head-to-Tail

Axiom:

i. ∀P , Q ∈ A.P, ∃a unique vector v ∈A.V such that v =P − Q.

ii. ∀Q ∈ A.P, ∀v ∈ A.V , ∃ a unique point P such that P − Q =v.

iii. ∀P , Q, R ∈A.P,

(

P − Q

)

(

Q − R

)

= P −R.

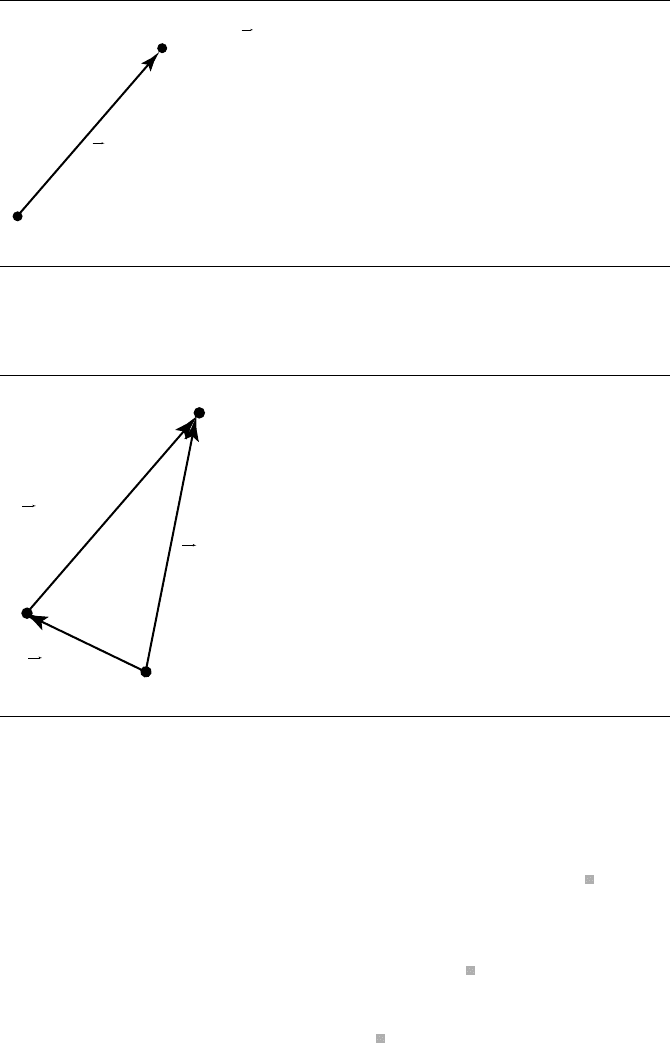
Note that condition (i) above can be rewritten as P = Q +v and also implies that

P = P +



0. Figure 3.23 shows the ﬁrst two axioms. The Head-to-Tail Axiom is de-

picted graphically in Figure 3.24.

Finally, we have another axiom (what DeRose calls the Coordinate Axiom), deﬁn-

ing two important multiplicative operations on points:

∀P ∈ A.P,1· P =P and 0 · P =



which simply tells us that multiplying a point by 1 gives us back the point, and

multiplying a point by 0 gives us back the zero vector for A.V .

A number of identities are worth listing (DeRose 1992):

i. Q − Q =



Proof If we set Q = R, then the Head-to-Tail Axiom can be rewritten as

(

P − Q

)

(

Q − Q

)

= P −Q, which means that

(

Q − Q

)



3.3 Afﬁne Spaces 81

P = Q + v

v = P – Q

Figure 3.23 Deﬁnition of point subtraction.

v =P – Q

w =P – R

u =Q – R

Figure 3.24 The Head-to-Tail axiom.

ii. R −Q =−

(

Q − R

)

Proof If we set P = R, then the Head-to-Tail Axiom can be rewritten as (R − Q) + (Q −

R) = R −R. Since R −R =



0, this implies that (R − Q) =−(Q − R).

iii. v + (Q − R) = (Q +v) − R

Proof Let v = P − Q. Substituting this into the Head-to-Tail Axiom gives us v + (Q −

R) = P − R. Substituting Q +v then gives us the result.

iv. Q − (R +v) = (Q − R) −v

Proof

Follows from the above by multiplying by −1.

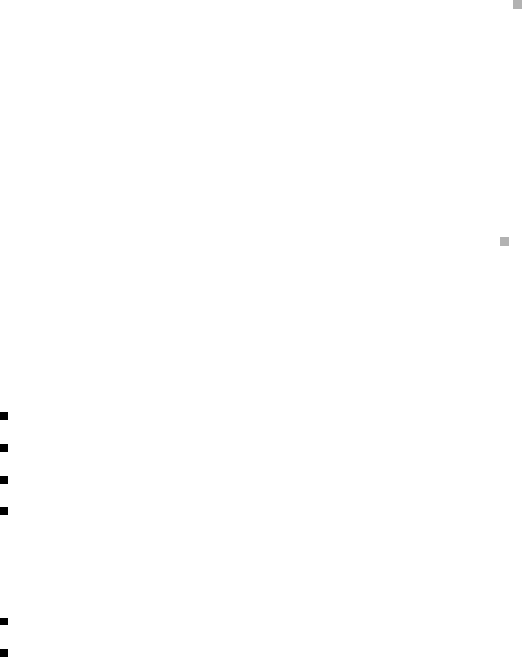
82 Chapter 3 Vector Algebra

v. P = Q + (P − Q)

Proof We can rewrite the Head-to-Tail Axiom, by invoking the deﬁnition of addition, as

P = R +(P − Q) + (Q − R). If we then substitute Q = R,wegetP = Q + (P −

Q) + (Q − Q). Since (Q − Q) =



0, we have the desired result.

vi. (Q +v) − (R +w) = (Q − R) + (v −w).

Proof

(Q +v) − (R +w)



(Q +v) − R





R − (R +w)



by Head-to-Tail Axiom



(Q +v) − R





(R − R) −w



by part (iv)



(Q +v) − R



−w by part (i)



(Q +v) − Q



[

Q − R

]

−w by Head-to-Tail Axiom



v + (Q − Q)



[

Q − R

]

−w by part (iii)

= (Q − R) + (v −w) by part (i)

Afﬁne Combinations

Recall that we can do the following:

Add two vectors together, yielding a third

Multiply a vector by a scalar, yielding a vector

Add a vector to a point, yielding another point

Subtract two points, yielding a vector

Note that we haven’t talked about the following:

Multiplying a point by a scalar

Adding two points together

The ﬁrst has no sensible interpretation whatsoever in an afﬁne space—what would it

mean to scale a location? Remember that we have no distinguished origin. The second

operation has no sensible interpretation either.

However, there is an operation that is sort of like adding two points together, and

it’s called an afﬁne combination. In an afﬁne combination, we effectively add together

fractions of points. Before you object too strongly to this as being even more bizarre

than adding or scaling points, consider the situation where we have two points P and

Q. We know now that these points can be considered to differ by a vector v =Q −P .

There are, of course, an inﬁnite number of points along the way from P to Q,each

some fraction of the way along v. Consider an arbitrary point R somewhere between

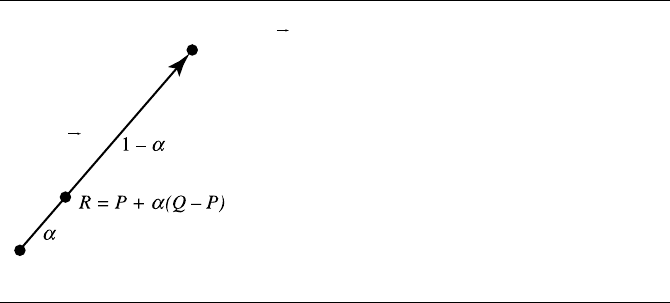
3.3 Afﬁne Spaces 83

Q = P + v

Figure 3.25 Afﬁne combination of two points.

P and Q. It divides the vector between them by some ratio, say, α :1− α. We then

can write

R = P + α

(

Q − P

)

which is depicted graphically in Figure 3.25. Let’s pretend for a minute we’re just

doing algebra. We could then rewrite the above as

R =

(

1 − α

)

P + αQ

or as

R = α

P + α

where α

+ α

= 1. We’ve just done two “forbidden” operations on points—scaling

by a vector and directly adding them. But, what we’ve just done is “clean up” the

original afﬁne combination, so we’ve done nothing technically wrong. However, this

notation is so convenient, it’s become common practice to employ it whenever we

know what we “really mean.” Let’s just “deﬁne our way out of the problem” by stating

the following: Wherever the expression

P + α

appears, if α

+ α

= 1, then it’s deﬁned to mean the point

P + α

(

Q − P

)