Schneider P., Eberly D.H. Geometric Tools for Computer Graphics

Подождите немного. Документ загружается.

814 Chapter 13 Computational Geometry Topics

containing the four points. The problem is to construct the one with minimum area.

The area as a function of c is

Area(c) =

πc(1 −b + c)

(4c − b

)

3/2

The minimum area occurs when c makes the derivative of area with respect to c

zero, Area



P(c; u, v) = S(v)c

+ T(u, v)c

− T(v, u)c − S(u) = 0

where S(v) =v

(v −1)

and T(u, v) = uv

(2v

+uv + u −3v +1). The maximum

root for P provides the correct value of c. The minimum area occurs at c = 1 when

P(1; u, v) = 0. This occurs when u = v or u

+ uv +v

− u − v = 0(oru + v = 1

or u =−v). These curves decompose the valid (u, v) region into subregions where

c>1orc<1. Numerically, the largest root can be found in regions where c<1

by applying Newton’s method to P(c)= 0 with an initial guess of c =1.Inregions

where c>1, Newton’s method can be applied to the inverted polynomial equation

P(1/c) = 0 with an initial guess of 1/c = 1.

Minimum-Area Ellipse for Fixed Center and Orientation

A special case of the minimum-area ellipse problem is to choose a center and orien-

tation, then compute the ellipse axis lengths that produce the minimum-area ellipse

with that center and orientation. Since the input points can be written in the coor-

dinate system with the speciﬁed center as the origin and the speciﬁed orientation for

the axes, we can analyze the problem when the center is the origin and the orientation

is the identity matrix. The ellipse equation is (x/a)

+(y/b)

=1, and the ellipse has

area πab, which we want to minimize for the input set of points.

The constraints on the axis lengths are a>0 and b>0. Additional constraints

come from requiring that each point (x

, y

) is inside the ellipse, (x

/a)

+ (y

/b)

≤ 1. The problem is to minimize the quadratic function ab subject to all the in-

equality constraints. Let u = 1/a

and v = 1/b

. The equivalent problem is to max-

imize f(u, v) = uv subject to the linear inequality constraints u ≥ 0, v ≥ 0, and

u + y

v ≤ 1 for all i. This is a quadratic programming problem, so the general

methods for such problems can be applied here (Pierre 1986). This type of program-

ming arises in other computational geometry applications and is being investigated

by various researchers (for example, Gaertner and Schoenherr 2000).

Although the general quadratic progamming methods apply here, the problem

may be solved in a more geometric way. The domain of f(u, v) is bounded by

a convex polygon with edges u = 0, v = 0, and other edges in the ﬁrst quadrant

determined by the point-in-ellipse containment constraints. Not all the constraints

necessarily contribute to the domain. The maximum of f must occur on the convex

13.11 Minimum Bounds for Point Sets 815

polygon boundary (not including u = 0orv = 0), so a smart search of that polygon

will produce the maximizing (u, v). This point can be a vertex or an interior edge

point. The constraint line that produces the smallest v on the u-axis is located by a

linear search. The other constraint lines are analyzed for intersection with this initial

line to ﬁnd the closest intersection to (0, v). This search produces the ﬁrst edge of the

convex polygon. If f is maximized at an interior point or at the u-minimum end

point, the problem is solved. Otherwise, the maximum of f on that edge occurs

at the u-maximum end point. The process of sorting constraint lines relative to

the constraint line that produced the u-maximum point is repeated. During the

iterations, as constraint lines are processed and/or determined not to ever participate

in the convex polygon boundary, they are marked as such to avoid processing them

again.

Minimum-Volume Ellipsoid

The algorithm for computing the minimum-volume ellipsoid containing a set of 3D

points is also similar to the one for minimum-volume spheres. The small problems

for a sphere involved ﬁnding the minimum sphere containing two, three, or four

points. For an ellipsoid, the small problems involve between four and nine points.

For nine points that form a convex polyhedron, the ellipsoid is computed as the solu-

tion of nine linear equations in the nine unknown coefﬁcients for a general quadric

equation. For four points that form a convex polyhedron, an algebraic formula exists

for the minimum-volume ellipsoid. The center is

C =



i=0

the average of the points, and M is the 3 ×3 matrix whose inverse is

−1



i=0

− C)(P

− C)

For the cases of 5 ≤ n ≤ 8, computing the minimum-volume ellipsoid is quite

difﬁcult. The volume function depends on 9 −n variables (coefﬁcients from the qua-

dratic equation). The 9 −n derivatives with respect to the variables are computed and

set to zero, each equation reducible to a polynomial equation. When n = 8, there is

one polynomial equation to solve in one unknown, a very tractable problem. How-

ever, when n = 5, there are four polynomial equations in four unknowns. Variables

can be reduced by elimination theory (Wee and Goldman 1995a, 1995b), but doing so

is subject to a lot of numerical problems, and the resulting single-variable polynomial

equation has an extremely large degree, so root ﬁnding itself will have a lot of numer-

ical problems. The other alternative is to numerically solve the system of polynomial

816 Chapter 13 Computational Geometry Topics

equations. It remains to be seen if anyone can produce a robust implementation of

the minimum-volume ellipsoid algorithm.

Numerical Minimization Methods

Although perhaps unappealing to computational geometers, the minimum-area or

minimum-volume bounding problems can be solved iteratively with numerical min-

imizers. In the case of circles, spheres, ellipses, or ellipsoids, the equations for these

quadratic objects have unknown coefﬁcients that are subject to inequality constraints

based on point-in-object requirements. The area and volume formulas are derived

based on the unknown coefﬁcients as variables. The result is a function to be mini-

mized subject to a set of inequality constraints, the topic of nonlinear programming.

The attractiveness of such an approach in an industrial setting is that it is easy to set

up and use existing robust nonlinear programming packages to solve the problem.

The speed and accuracy that a purely geometric approach might have is traded for

reduced development time, a viable trade-off in computer science that is typically

not considered by researchers in an academic environment.

13.12 Area and Volume Measurements

This section describes algorithms for computing areas of polygons, whether in 2D

or 3D, and for computing volumes of polyhedra. Various algorithms are shown with

algebraic, geometric, and analytic constructions.

13.12.1 Area of a 2D Polygon

Consider a triangle V

, V

 whose vertices are counterclockwise ordered. Setting

=(x

, y

), methods of basic algebra and trigonometry can be used to show that the

area of the triangle is

Area(V

, V

) =

det





111





(13.1)

Clearly, Area(V

, V

) = Area(V

, V

) = Area(V

, V

) since it does not

matter which vertex starts the counterclockwise ordering. However, if the order

is clockwise, then Area(V

, V

) = Area(V

, V

) = Area(V

, V

) =−

Area(V

, V

), all negative numbers. Thus, for any set of three vertices U, V , and

W , the function Area(U , V , W) as deﬁned by Equation 13.1 is referred to as the

signed area of the triangle formed by the vertices. If the vertices are counterclock-

13.12 Area and Volume Measurements 817

wise ordered, the signed area is positive. If the order is clockwise, the signed area is

negative. If the vertices are collinear, the signed area is zero.

Area as an Algebraic Quantity

Let V = (x, y) be an arbitrary point in the plane. The following algebraic identity is

true:

Area(V

, V

) = Area(V , V

, V

) + Area(V , V

, V

) + Area(V , V

, V

) (13.2)

The identity can be veriﬁed by expanding the determinants on the right-hand side of

the equation and performing algebraic operations to show that the result is the same

as the determinant on the left-hand side.

The formula for the area of a simple polygon P is inductive, the motivation being

the geometric intuition for Equation 13.2. The area for counterclockwise-ordered

vertices V

through V

n−1

and for an arbitrary point V is

Area(P) = Area(V , V

, V

) + Area(V , V

, V

) +···+Area(V , V

n−2

, V

n−1

)

+ Area(V , V

n−1

, V

) (13.3)

The proof of the formula uses mathematical induction. Suppose that the formula

is true for all simple polygons with n vertices. Now consider a polygon P



with

n + 1 vertices. As mentioned in Section 13.9, a polygon must have at least one ear,

a triangle that does not contain any other polygon vertices except the ones that form

the triangle. Relabel the vertices of P



so that the ear T is the triangle V

n−1

, V



and the polygon P obtained from P



by removing the ear is V

, ..., V

n−1

. The area

of T is

Area(T ) = Area(V , V

n−1

, V

) + Area(V , V

, V

) + Area(V , V

, V

n−1

)

by Equation 13.2. The area of P is

Area(P) = Area(V , V

, V

) + Area(V , V

, V

) +···+Area(V , V

n−2

, V

n−1

)

+ Area(V , V

n−1

, V

)

by the inductive hypothesis. The area of P



is the combined area Area(P



) =

Area(T ) + Area(P). When the two expressions are added together, the term

Area(V , V

, V

n−1

) from Area(T ) cancels with the term Area(V , V

n−1

, V

) from

Area(P). The ﬁnal sum is

Area(P



) = Area(V , V

, V

) + Area(V , V

, V

) +···+Area(V , V

n−1

, V

)

+ Area(V , V

, V

)

818 Chapter 13 Computational Geometry Topics

so the formula holds true for any P



with n + 1 vertices. By the principle of mathe-

matical induction, the formula is true for all integers n ≥ 3.

Using V =(0, 0), V

=(x

, y

), and Equation 13.1 for each term Area(



0, V

, V

i+1

an expansion of the right-hand side of Equation 13.3 leads to the formula that is

implementable in a computer program

Area(P) =

n−1



i=0

i+1

− x

i+1

) (13.4)

where indexing is modulo n. That is, x

= x

and y

= y

.Eachtermofthesum-

mation in Equation 13.4 requires two multiplications and one subtraction. A simple

rearrangement of terms reduces this to one multiplication and one subtraction per

term:

n−1



i=0

i+1

− x

i+1

) =

n−1



i=0

i+1

− y

i−1

) + x

i−1

− x

i+1

]

n−1



i=0

i+1

− y

i−1

) +

n−1



i=0

i−1

− x

i+1

)

n−1



i=0

i+1

− y

i−1

) + x

−1

− x

n−1



i=0

i+1

− y

i−1

)

The last equality is valid since x

= x

and y

−1

= y

n−1

based on the assumption

of indexing modulo n. The area is more efﬁciently calculated by a simple algebraic

observation:

Area(P) =

n−1



i=0

i+1

− y

i−1

) (13.5)

The FAQ for the Usenet newsgroup comp.graphics.algorithms attributes the for-

mula to Dan Sunday (2001), but the formula has occurred earlier in Usenet, posted

by Dave Rusin (1995) to the Usenet newsgroup sci.math. Given the simplicity of the

observation, it probably was known even earlier than 1995.

If the polygon P is not simple and contains a hole that is itself a polygon, the area

is computed as the difference of the area bounded by the outer polygon and the area

bounded by the inner polygon. If your polygon data structure allows such a polygon

to be stored in a single array so that the interior of the polygon is always to the left of

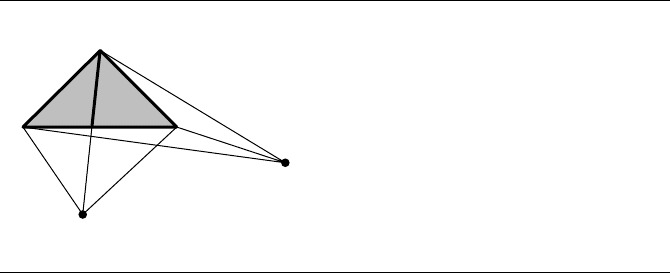
13.12 Area and Volume Measurements 819

Figure 13.81

Points U

and U

chosen for computing Equation 13.2. Only one edge of the triangle

is visible to the ﬁrst point. Two edges of the triangle are visible to the second point.

each edge, then the inner polygon is clockwise ordered. In this case Equation 13.5 is

still valid as shown without having to process the outer and inner polygons separately.

Area as a Geometric Quantity

Equation 13.2 has a geometric equivalent. Figure 13.81 shows a triangle and two

candidate points for V . The triangles that are formed by V and the edges that are

visible to it have negative signed areas. The other triangles have positive signed areas.

Notice that regardless of the choice of V , the partial signed areas of the overlap of the

triangles cancel, leaving only the area of the original triangle.

Area as an Analytic Quantity

The area of a 2D simple polygon P can also be derived using analytic methods from

calculus. Let the vertices of the polygon be V

= (x

, y

) for 0 ≤ i ≤ n − 1 and be

counterclockwise ordered. The interior of the polygon is the simply connected region

denoted R,soP is the boundary of region R. A formula for the area enclosed by

the polygon is obtained by an application of Green’s Theorem to a simply connected

region R with boundary curve P





∇·Fdxdy=



F ·nds

where F(x, y) =(F

(x, y), F

(x, y))is a differentiable vector ﬁeld,



∇·F =∂F

/∂x +

∂F

/∂y is the divergence of the vector ﬁeld, and n is an outward-pointing normal

820 Chapter 13 Computational Geometry Topics

vector to P. This formula can be found in many standard texts on calculus (for ex-

ample, Finney and Thomas 1996). If P is parameterized by (x(t), y(t)) for t ∈ [a, b],

a tangent vector is



t =(x



(t), y



(t)), where the prime indicates derivative with respect

to t and an outer normal is n = (y



(t), −x



(t)). The integral formula becomes





∇·Fdxdy=



F(x(t), y(t)) · (y



(t), −x



(t)) dt

The area formulation of Green’s Theorem arises when we choose F = (x, y)/2.

In this case



∇·F ≡ 1 and the integral on the left represents the area of R, the value

of which is determined by the integral on the right, an integral over the boundary P

of R:

Area(R) =



x(t)y



(t) − y(t)x



(t) dt (13.6)

Each edge of the polygon can be parameterized as (x

(t), y

(t)) = V

+ t(V

i+1

−

) for t ∈ [0, 1]. The integral over t becomes



x(t)y



(t) − y(t)x



(t) dt =

n−1



i=0



(t)y



(t) − y

(t)x



(t) dt

n−1



i=0



+ t(x

i+1

− x

)][y

i+1

− y

]

− [y

+ t(y

i+1

− y

)][x

i+1

− x

]dt

n−1



i=0

+ (x

i+1

− x

)/2][y

i+1

− y

]

− [y

+ (y

i+1

− y

)/2][x

i+1

− x

]dt

n−1



i=0

i+1

− x

i+1

)

where x

= x

and y

= y

. This is exactly Equation 13.4, obtained by algebraic

means.

13.12.2 Area of a 3D Polygon

Considera3DpolygonP that encloses a simply connected region in the plane

ˆn ·X = c,where ˆn is unit length. Let the vertices be V

for 0 ≤i ≤n − 1, and assume

that the vertices are counterclockwise ordered as you view the polygon from the side

13.12 Area and Volume Measurements 821

pointed to by ˆn. Equation 13.5 applies to the coordinates of the 3D polygon relative

to the plane. If ˆu and ˆw are unit-length vectors such that ˆu, ˆw, and ˆn are mutually

perpendicular, then V

= x

ˆu + y

ˆw + c ˆn and the planar points are (x

, y

) = ( ˆu ·

, ˆw · V

) for all i. The area is

Area(P) =

n−1



i=0

( ˆu · V

)( ˆw ·(V

i+1

− V

i−1

)) (13.7)

This formula, although mathematically correct, requires more computing time to

evaluate than necessary.

Area by Projection

A more efﬁcient approach is to observe that if ˆn =(n

, n

) is a unit-length normal

and n

= 0, then the area of an object that lies in a plane with normal ˆn is

Area(object) = Area(Projection

(object))/|n

That is, the area of the projection of P onto the xy-plane is calculated and adjusted

by the z-component of the normal. The result is a simple consequence of the surface

area formula for the graph of a function. If the plane is ˆn · (x, y, z) = c and n

= 0,

then z = f(x, y) = (c − n

x − n

y)/n

. The surface area of the graph of a function

f for (x, y) in a region R is





1 + f

+ f

dx dy

where f

= ∂f/∂x and f

= ∂f/∂y are the ﬁrst-order partial derivatives of f .Inthe

case of the plane mentioned earlier, f

=−n

, f

=−n

, and



1 + f

+ f



1 +











+ n

where the numerator of the fraction is 1 since ˆn is assumed to be unit length. There-

fore,





1 + f

+ f

dx dy =



1/|n

|dxdy = Area(R)/|n

822 Chapter 13 Computational Geometry Topics

The area of a polygon in the plane with normal ˆn can therefore be computed by

calculating the area of the 2D polygon obtained by using only the (x, y) components

of the polygon vertices, then dividing by the absolute value of the z-component of the

plane normal. However, if n

is nearly zero, numerical problems might arise. Better

is to use (x, y), (x, z),or(y, z) depending on which of |n

|, |n

|,or|n

| is largest,

respectively. The ﬁnal formula is

Area(P) =













n−1

i=0

i+1

− y

i−1

), |n

|=max



n−1

i=0

i+1

− z

i−1

), |n

|=max



n−1

i=0

i+1

− z

i−1

), |n

|=max

(13.8)

Area by Stokes’ Theorem

Another formula for the area appears in Arvo (1991) in an article entitled “Area of

Planar Polygons and Volume of Polyhedra.” That formula is

Area(R) =

ˆn ·

n−1



i=0

× P

i+1

) (13.9)

Given the counterclockwise ordering, the absolute values that appear in the actual

formula are not necessary. They are useful if you have an ordered set of vertices, but

you do not know if it is clockwise or counterclockwise. Replacing the formula P

U + y

V + c ˆn in the triple scalar product yields ˆn · P

× P

i+1

= x

i+1

− x

i+1

thereby showing the equivalence of the two formulas. However, ˆn is factored outside

the summation to reduce the n dot products to a single dot product. Each term

×P

i+1

requires 6 multiplications and 3 additions. The sum of the n cross products

requires 3(n − 1) additions. The dot product with ˆn requires 3 multiplications and

2 additions, and the ﬁnal product by one-half requires 1 multiplication. The total

calculation requires 6n + 4 multiplications and 6n − 1 additions. Clearly, Equation

13.8 is more efﬁcient to compute than Equation 13.9.

The article in Arvo (1991) mentions that Equation 13.9 can be derived from

Stokes’ Theorem, which states





∇×F ·ˆndσ =



F · d



where S is a manifold surface whose boundary is the bounded curve C.Thevector

ﬁeld F is normal to S at each position. The curl of F = (F

(x, y, z), F

(x, y, z),

(x, y, z)) is



∇×F =



∂F

∂y

−

∂F

∂z

∂F

∂z

−

∂F

∂x

∂F

∂x

−

∂F

∂y



13.12 Area and Volume Measurements 823

the differential d



R = (dx, dy, dz), but restricted to the curve C, and the differential

dσ represents an inﬁnitesimal element of the surface S.

In the case of a polygon in 3D, S is the planar region bounded by the polygon,

C is the polygon itself, ˆn is a unit-length normal vector (the polygon vertices are

counterclockwise ordered relative to ˆn), and F =ˆn × (x, y, z)/2, in which case



∇×

F =ˆn. The area is

Area(S) =



dσ =



ˆn ·ˆndσ =



ˆn × (x, y, z) · (dx, dy, dz)



ˆn · (x, y, z) × (dx, dy, dz)

If C is parameterized by (x(t), y(t)) for t ∈ [a, b], the formula becomes

Area(S) =



ˆn · (y(t)z



(t) − z(t)y



(t), z(t)x



(t) − x(t)z



(t), x(t)y



(t)

− y(t)x



(t)) dt

=ˆn ·





y(t)z



(t) − z(t)y



(t) dt,



z(t)x



(t) − x(t)z



(t) dt,



x(t)y



(t) − y(t)x



(t) dt



Observe that each integral is of the form shown in Equation 13.6. Thus, the

area of the polygon is a weighted sum of the areas of planar polygons obtained by

projection of the original polygon onto the three coordinate planes, the weights being

the components of the normal vector. Each of the integrals is given by Equation 13.5

with respect to the appropriate coordinates, so

Area(S) =

ˆn ·



n−1



i=0

i+1

− z

i−1

n−1



i=0

i+1

− x

i−1

n−1



i=0

i+1

− y

i−1

)



ˆn ·

n−1



i=0

× P

i+1

which is precisely Equation 13.9.