Schneider P., Eberly D.H. Geometric Tools for Computer Graphics
Подождите немного. Документ загружается.

794 Chapter 13 Computational Geometry Topics
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
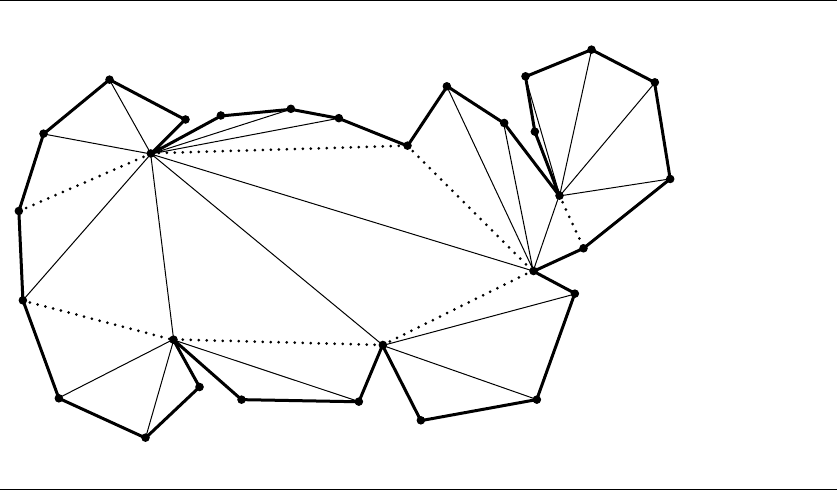
Figure 13.77
Canonical triangulations of the convex polygons in the minimum convex decomposition
of a polygon. The original polygon has edges shown in a heavy line. The diagonals used
in the decomposition are dotted. The diagonals used in the triangle fans for the canonical
triangulations are shown in a light line.
Consider condition 2 above where V
i
is a reflex vertex. The minimum decompo-
sitions of P
ik
use the diagonal (or edge) d
jk
for some j strictly between i and k,a
decomposition of P
jk
, and a decomposition of P
ij
where the latter decomposition
might or might not include d
ij
. The dynamic programming recurrence is
w
ik
= min
i<j<k, d
ij
and d
jk
exist
w
ij
+ w
jk
+ 2, if d
ij
included in decomposition
w
ij
+ w
jk
+ 1, otherwise
For a single value of j , popping the T
ij
stack will return the pairs in counterclockwise
order. We seek the last pair [s, t] such that d
tj
and d
jk
do not form a reflex angle
at V
j
. If there is no such pair, or if d
is
and d
ik
form a reflex angle at V
i
, then d
ij
is required in the convex decomposition of P
ik
and has weight w
ij
+ w
ik
+ 2 and
narrowest pair [j , j]. Otherwise a convex decomposition of P
ik
has been found with
weight w
ij
+ w
jk
+ 1 and narrowest pair [s, j ]. The pairs on the stack S
ik
for the
selected j always have j as a second index. The stack is constructed by pushing
each pair [x, j] that achieves minimum weight onto the stack only if the stack top
13.9 Polygon Partitioning 795
[x
0
, j] satisfies x
0
<x.Ifx
0
≥ x, the stack top is a narrower pair than the candidate
[x, j], so it is not pushed. The diagonal d
jk
is used in the decomposition, so either
j = k −1 (the diagonal is really a polygon edge) or at least one of V
j
or V
k
isareflex
vertex. This condition was referred to as “type A” in Keil and Snoeyink (1998), so
the pseudocode function is given that name. The double-ended stack is referred to
as
S(i,j) or T(i,j) depending on which end the stack operations are applied. The
diagonals are referred to as
D(i,j). A pair of indices that is used for tracking narrowest
pairs is
(pair.first,pair.second).
void TypeA(int i, int j, int k)
{
pair = null;
while (T(i,j) is not empty) {
tmpPair = T(i,j).Pop();
if (D(tmpPair.second,j ) and D(j, k) are not reflex at j)
pair = tmpPair;
}
if ((pair == null) or (D(i,pair.first) and D(i,k) are reflex at i)) {
P(i, k) decomposition uses D(i,j );
wtmp = w(i, j) + w(j, k) + 2;
narrow = [j, j];
} else {
P(i, k) decomposition does not use D(i, j);
wtmp = w(i, j) + w(j, k) + 1;
narrow = [pair.first, j];
}
if (S(i, k) is empty) {
w(i, k) = wtmp;
S(i, k).Push(narrow);
} else if (wtmp < w(i, k)) {
S(i, k).PopAll();
w(i, k) = wtmp;
S(i, k).Push(narrow);
} else if (wtmp == w(i, k)) {
if (narrow.first > S(i, k).Top().first)
S(i, k).Push(narrow);
}
}
Condition 3 is the symmetric case of condition 2 except that checking the vertices
V
i
and V
k
for reflexivity, in that order, means that V
i
is convex and V
k
is reflex. The
cases where both are reflex vertices is caught by condition 2. This condition was
796 Chapter 13 Computational Geometry Topics
referred to as “type B” in Keil and Snoeyink (1998), so the pseudocode function is
given that name.
void TypeB(int i, int j, int k)
{
pair = null;
while (S(j,k) is not empty) {
tmpPair = S(j, k).Pop();
if (D(i, j) and D(j, tmpPair.first) are not reflex at j)
pair = tmpPair;
}
if ((pair == null) or (D(pair.second, k) and D(i, k) are reflex at k)) {
P(i, k) decomposition uses D(j, k);
wtmp = w(i, j) + w(j, k) + 2;
narrow = [j, j];
} else {
P(i, k) decomposition does not use D(j, k);
wtmp = w(i, j) + w(j, k) + 1;
narrow = [j, pair.second];
}
if (S(i, k) is empty) {
w(i, k) = wtmp;
S(i, k).Push(narrow);
} else if (wtmp < w(i, k)) {
S(i, k).PopAll();
w(i, k) = wtmp;
S(i, k).Push(narrow);
} else if (wtmp == w(i, k)) {
while (narrow.second <= S(i, k).Top().second )
S(i, k).Push(narrow);
}
}
The main function for the minimum convex decomposition (MCD) is listed be-
low. The counterclockwise-ordered polygon vertices
V[n] are passed to the function.
The reflex vertices
RV[r] are also passed in order to maintain the O(nr
2
) order of the
algorithm. Precomputing the reflex vertices is an O(n) process.
void MCD(int n, Point V[n], int r, Point RV[r])
{
// size 2 problems
for(i=0,k=1;k<n;i++, k++)
w(i, k) = -1;
13.9 Polygon Partitioning 797
// size 3 problems
for(i=0,k=2;k<n;k++) {
if (Visible(i, k)) {
w(i, k) = 0;
S(i, k).Push([i + 1, i + 1]);
}
}
// size 4 and larger problems
for (size = 4; size <= n; size++) {
for(m=0;m<r;m++) {
i = RV[m]; k=i+size - 1;
if (k >= n) break;
if (Visible(i, k)) {
if (Reflex(k)) {
for(j=i+1;j<=k-1;j++) {
if (Visible(i, j) and Visible(j, k))
TypeA(i, j, k);
}
} else {
for(j=i+1;j<=k-2;j++) {
if (Reflex(j) and Visible(i, j) and Visible(j, k))
TypeA(i, j, k);
}
if (Visible(i,k-1))
TypeA(i,k-1,k);
}
}
}
for(m=r-1;m>=0;m--) {
k = RV[m]; i=k-size + 1;
if (i < 0) break;
if ((not Reflex(i)) and Visible(i, k)) {
if (Visible(i + 1, k))
TypeB(i,i+1,k);
for(j=i+2;j<=k-1;j++) {
if (Reflex(j) and Visible(i, j) and Visible(j, k))
TypeB(i, j, k);
}
}
}
}
}
798 Chapter 13 Computational Geometry Topics
In the size 4 or larger block of code, the function is O(nr
2
) in time since TypeA
or TypeB is called only for at least two reflex vertices or for one reflex vertex and one
polygonedge.Theworkdoneineachcallto
TypeA or TypeB is O(1) plus the number
of pairs popped from the stacks. Since at most one pair is added to two stacks, at most
O(nr
2
) elements can be popped. The memory requirements are also O(nr
2
) due to
the space required for the stacks.
At first glance, the size 3 block of code appears to be O(n
2
) in time, O(n) for the
outer loop and O(n) for each straightforward visiblity test that checks if V
i
, V
i+2
is a diagonal. This potentially offsets the O(nr
2
) time for the size 4 and larger block
when r is much smaller than n. Since the size is 3, the visibility test is really checking
if V
i
, V
i+2
is an ear. As shown at the beginning of this section, the ear test can be
implemented by testing for containment of only the reflex vertices in the triangle
V
i
, V
i+1
, V
i+2
. The size 2 block can therefore be implemented to take O(nr) time.
Miscellaneous
Partitioning of a polygon can also be accomplished by using BSP trees. The BSP
tree for a polygon is computed as shown in Section 13.1. The leaf nodes of the tree
represent a convex partitioning of the plane. The positive/negative tags allow you
to identify those leaf nodes that correspond to convex subpolygons of the original
polygon. The union of these is the original polygon. This type of decomposition
inserts points into the polygon, unlike the methods discussed in earlier sections that
just use the original vertices. If a triangulation of the polygon is needed, the convex
subpolygons can be fanned into triangles.
The problem of partitioning polyhedra into tetrahedra is the natural extension
of partitioning a planar polygon. To date, the fastest algorithm to triangulate non-
convex polyhedra is presented in Chazelle and Palios (1990). The asymptotic order
is O(n log r + r
2
log r),wheren is the number of faces and r is the number of
reflex edges. Another relevant paper is Hershberger and Snoeyink (1997), which de-
composes a nonconvex polyhedron into convex pieces effectively by using BSP trees.
Practically speaking, the BSP tree approach is easy to implement and has acceptable
performance for the decomposition.
13.10
Circumscribed and Inscribed Balls
A triangle in two dimensions has two special circles associated with it, a circumscribed
circle that contains the vertices of the triangle and an inscribed circle that is the largest-
area circle contained in the triangle. Although the inscribed circle has the largest area
of all circles contained in the triangle, the circumscribed circle is not necessarily the
smallest-area circle containing the triangle. This is clearly the case when the triangle
vertices are nearly collinear, in which case the circumscribed circle has an extremely
large radius, but the minimum-area circle containing the triangle has a diameter

13.10 Circumscribed and Inscribed Balls 799
Figure 13.78 Circumscribed and inscribed circles for a triangle.
equal to the length of the longest edge. Figure 13.78 illustrates the circumscribed and
inscribed circles for a triangle. The circumscribed circle is solid, and the inscribed
circle is dotted. Our goal is to construct these circles for a specified triangle.
Similarly, a tetrahedron in three dimensions has two special spheres associated
with it, a circumscribed sphere that contains the vertices of the tetrahedron and an
inscribed sphere that is the largest-volume sphere contained in the tetrahedron. The
circumscribed sphere is not necessarily the smallest-volume sphere containing the
tetrahedron.
The ideas extend to higher dimensions. The generalization of triangle (2D) and
tetrahedron (3D) to n dimensions is called a simplex. This object has n + 1 vertices,
each vertex connected to every other vertex. If the vertices are V
i
for 0 ≤ i ≤ n, then
the edges e
i
= V
i
− V
0
are required to be linearly independent vectors. To illustrate
what this constraint means, in 3D it prevents the case of four points being coplanar,
in which case the tetrahedron is flat and has no volume. Two special hyperspheres
(mathematical term) or balls (the vernacular) for a simplex are the circumscribed
ball that contains the vertices of the simplex and the inscribed ball that is the largest-
volume ball contained in the simplex.
The construction of the circumscribed and inscribed balls involves setting up sys-
tems of n linear equations in n unknowns. Because of the simplicity of the construc-
tion, there is no need to handle the 2D and 3D cases separately to provide intuition.
13.10.1 Circumscribed Ball
A circumscribed ball for the simplex is that ball passing through all the vertices of the
simplex. The center of this ball, C, is equidistant from the vertices, say, of distance r.
The constraints are
C −V
i
=r,0≤ i ≤ n
800 Chapter 13 Computational Geometry Topics
Squaring the equations, expanding the dot products, and subtracting the squared
equation for i = 0 yields 2(V
i
− V
0
) · (C − V
0
) −V
i
− V
0
2
for 1 ≤ i ≤ n. This is
a system of linear equations in the form AX = B, where the ith row of A is V
i
− V
0
written as a 1 ×n vector, the ith row of B is V
i
−V
0
2
/2, and X =C −V
0
written as
an n ×1 vector. Since the edges sharing V
0
are linearly independent, A is an invertible
matrix and the linear system has a unique solution X =A
−1
B. Therefore, the center
of the circumscribed ball is C =V
0
+A
−1
B. Once the center has been calculated, the
radius of the circumscribed ball is r =C − V
0
.
Dimension 2
Define V
i
= (x
i
, y
i
) for i = 0, 1, 2. The triangle is assumed to be counterclockwise
ordered. Define X
i
= x
i
− x
0
and Y
i
= y
i
− y
0
. The area of the triangle is
A =
1
2
det
X
1
Y
1
X
2
Y
2
and the center (x, y) and radius r are
x =x
0
+
1
4A
(Y
2
L
2
10
− Y
1
L
2
20
)
y =y
0
+
1
4A
(X
1
L
2
20
− X
2
L
2
10
)
r =
(x −x
0
)
2
+ (y − y
0
)
2
where L
ij
=V
i
−V
j
. It can be shown that r =L
10
L
20
L
12
/(4A), the product of the
edge lengths divided by four times the area. It can also be shown (Blumenthal 1970)
that the radius is a solution to the Cayley-Menger determinant equation
det
01111
10L
2
10
L
2
20
r
2
1 L
2
10
0 L
2
21
r
2
1 L
2
20
L
2
21
0 r
2
1 r
2
r
2
r
2
0
= 0
Dimension 3
Define V
i
=(x
i
, y
i
, z
i
) for i =0, 1, 2, 3. The tetrahedron V
0
, V
1
, V
2
, V
3
is ordered so
that it is isomorphic to the canonical one (0, 0, 0), (1, 0, 0), (0, 1, 0), (0, 0, 1). Define

13.10 Circumscribed and Inscribed Balls 801
X
i
= x
i
− x
0
, Y
i
= y
i
− y
0
, and Z
i
= z
i
− z
0
. The volume of the tetrahedron is
V =
1
6
det
X
1
Y
1
Z
1
X
2
Y
2
Z
2
X
3
Y
3
Z
3
and the center (x, y, z) and radius r are
x =x
0
+
1
12V
+(Y
2
Z
3
− Y
3
Z
2
)L
2
10
− (Y
1
Z
3
− Y
3
Z
1
)L
2
20
+ (Y
1
Z
2
− Y
2
Z
1
)L
2
30
y =y
0
+
1
12V
−(X
2
Z
3
− X
3
Z
2
)L
2
10
+ (X
1
Z
3
− X
3
Z
1
)L
2
20
− (X
1
Z
2
− X
2
Z
1
)L
2
30
z = z
0
+
1
12V
+(X
2
Y
3
− X
3
Y
2
)L
2
10
− (X
1
Y
3
− X
3
Y
1
)L
2
20
+ (X
1
Y
2
− X
2
Y
1
)L
2
30
r =
(x −x
0
)
2
+ (y − y
0
)
2
+ (z − z
0
)
2
where L
ij
=V
i
− V
j
. It can be shown (Blumenthal 1970) that the radius is a
solution to the Cayley-Menger determinant equation
det
011111
10L
2
10
L
2
20
L
2
30
r
2
1 L
2
10
0 L
2
21
L
2
31
r
2
1 L
2
20
L
2
21
0 L
2
32
r
2
1 L
2
30
L
2
31
L
2
32
0 r
2
1 r
2
r
2
r
2
r
2
0
= 0
13.10.2 Inscribed Ball
An inscribed ball for the simplex is the ball of maximum volume contained in the
simplex. Necessarily the ball is tangent to all faces of the simplex. The center of the
ball, C, is equidistant from the faces, say, of distance r. The distance to each face is
obtained as the length of the projection of C − V onto the inner-pointing, unit-
length normal vector to a face that contains V. The projections are
ˆn
i
· (C − V
i
) = r,0≤ i ≤ n
where ˆn
i
is the inner-pointing, unit-length normal to the hyperface determined by
the vertices V
imod(n+1)
, V
(i+1)mod(n+1)
,...,V
(i+n−1)mod(n+1)
. This is a linear system
of n + 1 equations in the n + 1 unknowns (C, r), where each equation is written as
( ˆn
i
, −1) · (C, r) =ˆn
i
· V
i
. Define the (n + 1) × (n + 1) matrix A to be that matrix

802 Chapter 13 Computational Geometry Topics
whose ith row is the vector ( ˆn
i
, −1) written as a 1 × (n + 1) vector. Define the
(n + 1) × 1vectorB to be that vector whose ith row is ˆn
i
· V
i
. The linear system
is A(C, r) = B and has solution (C, r) = A
−1
B, where the left-hand side is thought
of as an (n + 1) × 1vector.
Dimension 2
Define V
i
=(x
i
, y
i
) for i =0, 1, 2, and for notation’s sake, let V
3
=V
0
. The unit-length
edge directions are
ˆ
d
i
= (V
i+1
− V
i
)/L
i
with L
i
=V
i+1
− V
i
for 0 ≤ i ≤ 2. The
inner-pointing unit-length normals are ˆn
i
=−
ˆ
d
⊥
i
,where(x, y)
⊥
= (y, −x).
The radius and center of the inscribed circle can be constructed as shown pre-
viously. However, the solution has a nice symmetry about it if the center is written
in barycentric coordinates as C = t
0
V
0
+ t
1
V
1
+ t
2
V
2
,wheret
0
+ t
1
+ t
2
= 1. In this
form the equations r =ˆn
i
· (C − V
i
) become r = t
2
L
2
ˆ
d
0
·ˆn
2
, r = t
0
L
0
ˆ
d
1
·ˆn
0
, and
r = t
1
L
1
ˆ
d
2
·ˆn
1
. The area A of the triangle is given by 2A = L
0
L
2
ˆ
d
0
·ˆn
2
= L
1
L
0
ˆ
d
1
·
ˆn
0
= L
2
L
1
ˆ
d
2
·ˆn
1
. Combining these with the previous equations yields t
0
= RL
1
/
(2A), t
1
= RL
2
/(2A), and t
2
= RL
0
/(2A). Summing the t
i
we have 1 = (L
0
+ L
1
+
L
2
)r/(2A), in which case r =2A/(L
0
+L
1
+L
2
). Again for the sake of notation, de-
fine
i
= L
(i−1)mod3
. The value
i
is the length of the edge opposite vertex V
i
. Define
L = L
0
+ L
1
+ L
2
=
0
+
1
+
2
. In this form the radius and center are
r =
2A
L
, C =
2
i=0
i
L
V
i
Dimension 3
Define V
i
= (x
i
, y
i
, z
i
) for i = 0, 1, 2, 3. The tetrahedron V
0
, V
1
, V
2
, V
3
is ordered
so that it is isomorphic to the canonical one (0, 0, 0), (1, 0, 0), (0, 1, 0), (0, 0, 1).The
inner-pointing normals for this configuration are n
0
=(V
1
−V
0
) ×(V
2
−V
0
)/(2A
0
),
where A
0
is the area of the face to which n
0
is normal; n
1
= (V
3
− V
1
) × (V
2
−
V
1
)/(2A
1
),whereA
1
is the area of the face to which n
1
is normal; n
2
= (V
3
− V
2
) ×
(V
0
− V
2
)/(2A
2
),whereA
2
is the area of the face to which n
2
is normal; and n
3
=
(V
1
− V
3
) × (V
2
− V
3
)/(2A
3
),whereA
3
is the area of the face to which n
3
is normal.
As in dimension 2, the solution is nicely expressed when the center is repre-
sented in barycentric coordinates C =
3
i=0
t
i
V
i
with
3
i=0
t
i
=1. The equations r =
n
i
· (C − V
i
) become r = t
3
n
0
· (V
3
− V
0
), r = t
0
n
1
· (V
0
− V
1
), r = t
1
n
2
· (V
1
− V
2
),
and r = t
2
n
3
· (V
2
− V
3
). The volume of the tetrahedron is given by the following
equations involving triple scalar products, 6V =[V
1
−V
0
, V
2
−V
0
, V
3
−V
0
]=[V
0
−
V
1
, V
3
− V
1
, V
2
− V
1
] = [V
3
− V
2
, V
0
− V
2
, V
1
− V
2
] = [V
2
− V
3
, V
1
− V
3
, V
0
− V
3
].
Combining these with the previous equations yields t
0
=RA
1
/(3V), t
1
=RA
2
/(3V),
t
2
= RA
3
/(3V), and t
3
= RA
0
/(3V). Summing the t
i
we have 1 = (A
0
+ A
1
+ A
2
+

13.11 Minimum Bounds for Point Sets 803
A
3
)r/(3V), in which case r =3V /(A
0
+A
1
+A
2
+A
3
). Define α
i
=A
(i−1)mod4
.The
value α
i
is the area of the face opposite vertex V
i
. Define A = A
0
+ A
1
+ A
2
+ A
3
=
α
0
+ α
1
+ α
2
+ α
3
. In this form the radius and center are
r =
3V
A
, C =
3
i=0
α
i
A
V
i
Dimension n
The same construction using barycentric coordinates for C may be applied in general
dimensions. The radius and center are
r =
nV
S
, C =
n
i=0
σ
i
S
V
i
where V is the volume of the simplex, σ
i
is the surface area of the hyperface opposite
vertex V
i
, and S =
n
i=0
σ
i
is the total surface area of the simplex.
13.11
Minimum Bounds for Point Sets
In this section, let the point set be {P
i
}
n−1
i=0
with n ≥ 2. In the discussions in this
section, all points are assumed to be unique. However, an implementation must be
prepared to handle sets that contain multiple copies of the same point or even two
points that are nearly the same point (within some floating-point tolerance). This
section covers the topics of minimum-area rectangles, circles, and ellipses in 2D and
minimum-volume boxes, spheres, and ellipsoids in 3D.
13.11.1 Minimum-Area Rectangle
It is evident that the only points that need to be considered are the vertices of the
convex hull of the original point set. The problem is therefore reduced to finding the
minimum-area rectangle that contains a convex polygon with ordered vertices P
i
for
0 ≤i<N. The rectangle is not required to be axis aligned with the coordinate system
axes. It is the case that at least one of the edges of the convex polygon must be con-
tained by an edge of the minimum-area rectangle. Given that this is so, an algorithm
for computing the minimum-area rectangle need only compute the tightest-fitting
bounding rectangles whose orientations are determined by the polygon edges.
