Schneider P., Eberly D.H. Geometric Tools for Computer Graphics

Подождите немного. Документ загружается.

784 Chapter 13 Computational Geometry Topics

11 16

Figure 13.68 The sample polygon after trapezoids are merged into maximally sized ones.

Figure 13.69 The sample polygon as a union of monotone polygons. The two polygons are drawn

in light gray and dark gray. The horizontal line segments from the trapezoidal de-

composition are still shown.

on the trapezoid’s top edge. Similarly, a cusp that opens upward occurs on the top

edge of some trapezoid. A line segment is added from that cusp to the vertex on the

trapezoid’s bottom edge. It is possible that both end points of the newly added seg-

ment are cusps. Figure 13.69 shows the polygon of the ongoing example. Only one

line segment needed to be added, from a downward opening cusp to a vertex on the

trapezoid’s top edge. The polygon consists of two monotone polygons.

The last paragraph had the assumption that no two vertices have the same y-

value. This can, of course, happen in practice. The algorithm for adding line segments

to form monotone polygons must be slightly modiﬁed to handle this case.

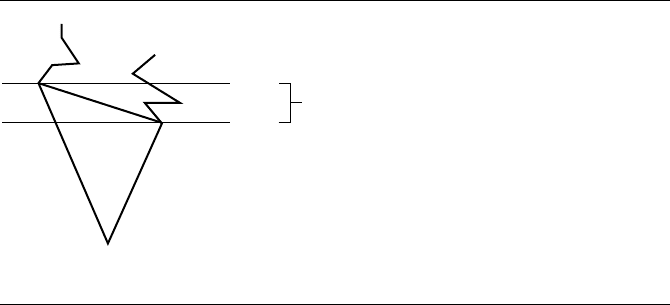
13.9 Polygon Partitioning 785

min

Polygon is monotonic in strip

using edge 具V

min

, V

典 or

edge 具V

, V

典

Figure 13.70 If the triangle at an extreme vertex is an ear, removing the ear yields another mono-

tone polygon.

Monotone Polygon Triangulation

The polygons obtained in the decomposition of a simple polygon are monotone with

respect to the y-axis. That is, any line in the x-direction intersects a y-monotone

polygon in one point (an extreme point in the y-direction), in two points (the typical

case), or along an entire edge of the polygon (edge is horizontal). The triangulation

of a monotone polygon requires only O(n) time to compute (Fournier and Mon-

tuno 1984). The method involves a greedy algorithm that removes triangles from the

extreme ends of the polygon.

First, let us just try to remove a triangle from an extreme end of the polygon

to see what issues arise. Let V

min

and V

max

be the extreme points of the polygon.

The polygon has two monotonic chains referred to as the left chain and the right

chain.LetV

= (x

, y

) be the vertex on the left chain that is adjacent to V

min

, and

let V

= (x

, y

) be the adjacent one on the right chain. For the sake of argument,

assume y

≥ y

. Otherwise, we can make the same argument with the roles of the

chains reversed. If the triangle V

, V

min

, V

 is an ear, that ear can be removed and

added to the list of triangles in the triangulation. The edge V

min

, V

of the left chain

is removed and replaced by the edge V

, V

. The modiﬁed chain is still monotonic

in the y-direction, so the process can be repeated on the new monotone polygon at

its minimum vertex. Figure 13.70 provides an illustration.

The problem with this approach is that it requires determining whether or not the

triangle at the minimum vertex is an ear. In fact, the minimum vertex might not be

an ear tip. Figure 13.71 shows two types of failure that can occur. Failure to be an ear

tip can occur simply because the next edge on the right chain V

, W  is inside the

triangle V

, V

min

, V

 (Figure 13.71(a)). The failure might also be a result of more

complex behavior, for example, a chain of vertices in the strip y

<y<y

that are

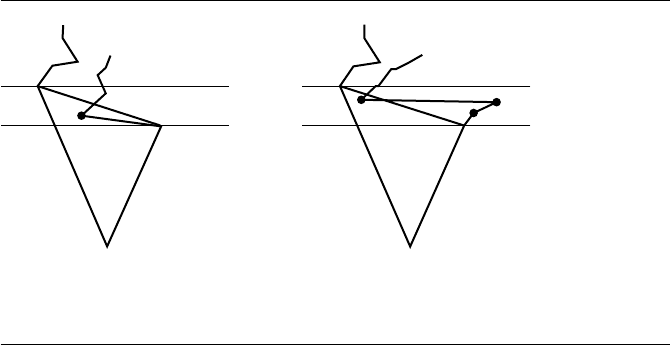
786 Chapter 13 Computational Geometry Topics

min

(a) (b)

Figure 13.71 Failure of triangle V

, V

min

, V

 to be an ear.

outside the mentioned triangle, but the next vertex W in that chain being inside the

triangle (Figure 13.71(b)).

The conﬁguration in Figure 13.71(a) is easy to handle. The triangle V

min

, V

, W 

is an ear and can be removed. The edge V

min

, V

 in the right chain is removed and

replaced by V

min

, W. The right chain is still monotonic, so the reduced polygon is

monotonic and the process can be repeated. The removal can occur even if W is not

inside V

, V

min

, V

 as long as V

isaconvexvertex.

The conﬁguration in Figure 13.71(b) is the more interesting one. A sequence of

reﬂex vertices occur, called a reﬂex chain. In the ﬁgure, the predecessor U to W is the

ﬁrst vertex occurring after the reﬂex chain, so it is a convex vertex, and the very next

edge with end point W makes the reﬂex chain invisible from V

. All vertices in the

reﬂex chain, however, are visible to W , so all triangles formed by W and the vertices

in the reﬂex chain can be removed. The right chain reduces to a monotonic chain

whose ﬁrst three vertices are V

min

, W , and U . The reduced polygon is still monotonic.

Even so, the conﬁguration in Figure 13.71(b) is still not representative of other

conﬁgurations. The vertex W might not be in the triangle V

, V

min

, V

, yet the tri-

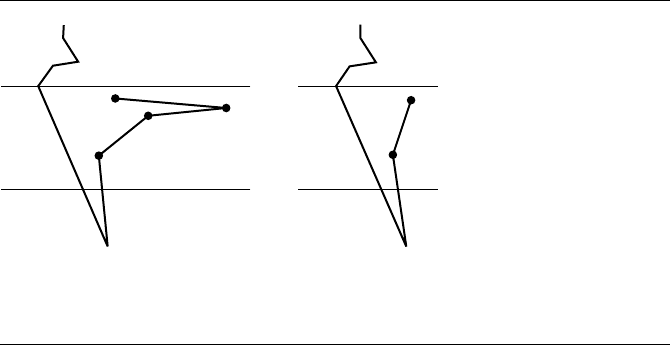
angles formed by it and the reﬂex chain vertices can be removed. Worse is that not all

of the reﬂex chain vertices are visible to W. Figure 13.72 illustrates this conﬁguration.

After all the valid triangles are removed, W will be the next vertex to be added to the

reﬂex chain.

The ﬁnal variation is that W might occur above the strip rather than inside it. In

this case, the vertices in the reﬂex chain are all visible to V

. It is sufﬁcient to form

all triangles containing V

and the reﬂex vertices and remove them. Observe that in

this case, the triangle V

, V

min

, V

 is an ear of the polygon, exactly the motivation

originally for attempting to remove that triangle ﬁrst. The valid triangles are removed

13.9 Polygon Partitioning 787

min

(a) (b)

Figure 13.72 (a) Not all reﬂex chain vertices are visible to W. (b) Removal of the triangles leads to

W being the next vertex to be added to the reﬂex chain.

starting with this one. Figure 13.73 illustrates this. The difference between the con-

ﬁgurations in Figures 13.72 and 13.73 is the y-ordering of V

and W . To handle this,

the vertices from both left and right chains must be sorted in a single list. Since the

left and right chains are already sorted, the full sort requires a merge of two sorted

lists, an operation that is performed in O(n) time.

The pseudocode for triangulating a y-monotone polygon is listed below. The

left and right chains are passed separately, each having the vertex with minimum

y-value in the slot zero and each having the vertex with maximum y-value in the

corresponding last slot.

void TriangulateMonotone(int NL, Point LChain[NL], int NR, Point RChain[NR],

TriangleList TList)

{

// Each node in the list contains a vertex and an identifier of the

// chain to which the vertex belongs.

VertexList VList = MergeChains(NL, LChain, NR, RChain);

// A list whose front corresponds to the y-minimum vertex and whose rear

// corresponds to the y-maximum vertex.

ReflexChain RList;

// Initialize the chain with the first two vertices. AddMax(VList) places

// the specified list node at the end of the chain. A side effect of the

// operation is to provide RList with a ’whichChain’ tag, L or R, about

788 Chapter 13 Computational Geometry Topics

// which of the left or right polygon chains the current reflex chain belongs.

RList.AddMax(VList); VList = VList.Next();

// VList points to the third vertex in the list.

while (VList is not empty ) {

// Max() is an accessor to the rear of the reflex chain that contains

// the vertex of maximum y-value.

if (VList.Previous() is equal to RList.Max()) {

// VList.vertex is on the same chain as the reflex chain

if (RList.Max() is a convex vertex) {

TList.Add(RList.Max().Previous().vertex);

TList.Add(RList.Max().vertex);

TList.Add(VList.vertex);

// Remove vertex from reflex chain and from vertex list. These

// are the same vertex.

RList.RemoveMax();

VList.Previous().RemoveSelf();

if (RList is empty)

VList = VList.Next();

} else {

// RList.Max() is a reflex vertex, no collinear allowed

RList.AddMax(VList);

VList = VList.Next();

}

} else {

// VList.vertex is on the opposite chain to the reflex chain.

// Min() is an accessor to the front of the reflex chain that

// contains the vertex of minimum y-value.

TList.Add(RList.Min().vertex);

TList.Add(RList.Min().Next().vertex);

TList.Add(VList.vertex);

// Remove vertex from reflex chain and from vertex list. These

// are the same vertex.

RList.RemoveMin();

VList.Previous().RemoveSelf();

if (RList is empty)

VList = VList.Next();

}

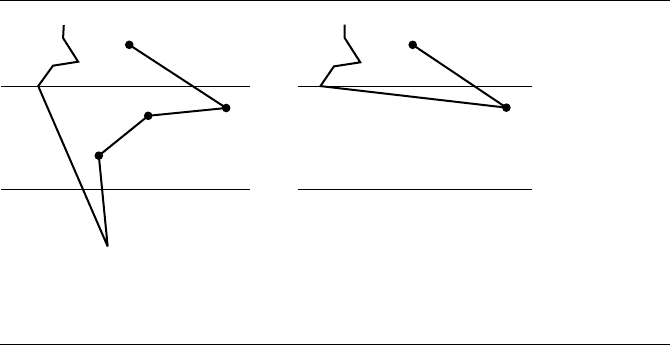
13.9 Polygon Partitioning 789

min

(a) (b)

Figure 13.73 (a) W occurs above the current strip, V

is visible to all reﬂex chain vertices. (b) Re-

moval of the triangles leads to a reduced monotone polygon, so the process can be

repeated.

In summary, a simple polygon is triangulated by decomposing it into horizontal

strips of trapezoids, merging the trapezoids into maximal pieces, connecting vertices

between top and bottom trapezoid edges to form y-monotone polygons, then trian-

gulating the monotone polygons.

A variation on this algorithm presented in O’Rourke (1998) ﬁnds monotone

mountains. These are monotone polygons for which one of the monotone chains

is a single line segment. Triangulating a monotone mountain is easier than triangu-

lating a monotone polygon because it is easier to identify ears and remove them, one

at a time. An implementation looks similar to the ear clipping presented earlier in

this chapter.

13.9.4 Convex Partitioning

A polygon triangulation is a special case of partitioning the polygon into convex sub-

polygons, the number of subpolygons being n − 2 for n vertices. A more general

problem is to partition the polygon into convex subpolygons, but minimize the num-

ber of such subpolygons. Clearly a triangulation does not do this. A square has two

triangles in its triangulation, but is already convex, so the optimum number of con-

vex pieces is one. Convex partitioning is useful for allowing artists to construct 3D

polygonal models without concern for generating nonconvex faces. The models can

be postprocessed to partition the faces so that all faces are convex. Moreover, gener-

ating the minimum number of convex faces is useful for a renderer whose primitives

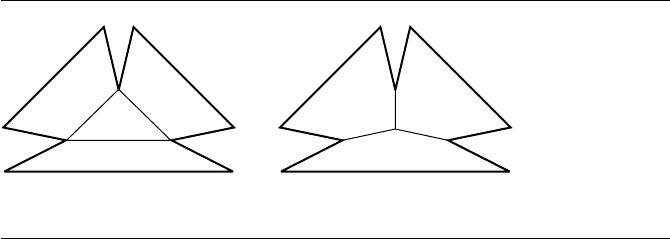
790 Chapter 13 Computational Geometry Topics

(a) (b)

Figure 13.74

(a) Partition using only vertices. (b) Partition using an additional point interior to

the polygon.

include convex polygons. By minimizing the number of input primitives, the setup

costs for rasterizing the polygons is minimized.

A triangulation always uses diagonals of the polygon as edges of the triangles.

Optimal convex partitioning might require additional points and segments to be

speciﬁed in order to obtain the minimum number of subpolygons (see Figure 13.74).

The convex partitioning methods mentioned in this section only use diagonals for

the construction.

Chazelle showed that the minimum number µ of convex subpolygons in a par-

tition is bounded by r/2+1 ≤ µ ≤ r + 1, where r is the number of reﬂex vertices

of the polygon. The bounds are tight since it is easy to construct two polygons, one

whose optimum partition attains the lower bound and one whose optimum partition

attains the upper bound. Algorithms that construct an optimum partition tend to run

slowly (in asymptotic terms). Algorithms that partition rapidly tend not to obtain the

optimum number of pieces. In this section we provide an example of each.

A Suboptimal But Fast Convex Partitioning

A fast and simple algorithm for producing a convex partitioning that is suboptimal is

presented by Hertel and Mehlhorn (1983). However, it is known that the number of

convex subpolygons is no larger than four times the optimal number. Given a convex

partition involving diagonals, a diagonal incident to a vertex V is said to be essential

for that vertex if removing the diagonal shared by two convex subpolygons leads to

a union that is not convex (at V ). Otherwise the diagonal is said to be inessential.A

diagonal connecting two convex vertices is clearly inessential. It must be that for a

diagonal to be essential for V , the vertex must be reﬂex. However, a reﬂex vertex can

be an end point for an inessential diagonal (see Figure 13.75).

The algorithm is simple. Start by triangulating the polygon. Remove each inessen-

tial diagonal, one at a time. The triangulation has O(n) diagonals, so the removal

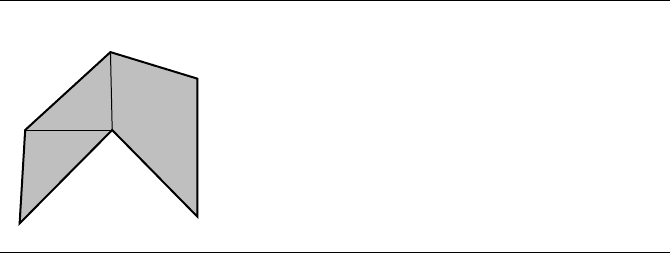
13.9 Polygon Partitioning 791

Figure 13.75 Ve r t ex V

is reﬂex. The diagonal V

, V

is inessential. The diagonal V

, V

is essen-

tial for V

phase is O(n). In theory the triangulation can be done in O(n) time, so this subop-

timal partitioning can be done in O(n) time. But as mentioned before, the triangu-

lation algorithms implemented in practice are asymptotically slower, so the time for

partitioning is dominated by the triangulation time.

An Optimal Convex Partitioning

An optimal partitioning algorithm by Keil and Snoeyink (1998) is described in

this section. The algorithm uses only diagonals and has an asymptotic run time of

O(nr

),wheren is the number of polygon vertices and r is the number of reﬂex

vertices. The algorithm is based on dynamic programming (Bellman 1987).

The simple polygon has counterclockwise-ordered vertices V

for 0 ≤ i<n.The

diagonals are denoted by d

=V

, V

 for i<j. The only diagonals that need to be

considered are those that have at least one end point that is a reﬂex vertex. A diagonal

with two convex vertex end points can clearly be removed to join two convex sub-

polygons into a single convex subpolygon. Thus, an optimal convex partitioning will

never have diagonals with both end points being convex vertices. It is not necessary

that a diagonal connecting two reﬂex vertices be part of the optimal partitioning.

Dynamic programming ﬁnds the optimal solution to a problem by combining

optimal solutions to subproblems of the same form as the original. Given a diagonal

, the subproblem involves the subpolygon P

whose vertices are V

, V

i+1

, ..., V

This polygon must itself be optimally partitioned into convex pieces. The size of this

problem is the number of vertices in the polygon. The original polygon is P

0,n−1

and

has size n. The subpolygon P

has size k − i + 1. The weight w

of the problem

is the minimum number of diagonals in a convex partitioning of P

. The optimal

partitioning involves computing the weight w

0,n−1

of the original polygon P

0,n−1

792 Chapter 13 Computational Geometry Topics

convention is made that the edge d

0,n−1

is considered to be a diagonal. The optimiza-

tion is done from the bottom up, so for initialization we need w

i,i+1

=−1 for all i.

As indicated in Keil (1985), P

can have exponentially many decompositions that

attain weight w

. However, by deﬁning equivalence classes of decompositions, the de-

composition of P

is simpliﬁed. Each decomposition of P

has an associated pair of

vertex indices [a, b], with possibly a =b, the vertices with indices a, i, k, b occurring

in clockwise order in one of the convex polygons in the decomposition. Two decom-

positions are equivalent if they have the same weight and the same associated pair of

indices. Additionally, some minimum decompositions are labeled as narrowest pairs,

those whose convex regions in a small neighborhood of d

do not contain the con-

vex region of any other minimum decomposition of P

. Keil (1985) observed that

only narrowest pairs need to be considered when constructing solutions to the sub-

problem P

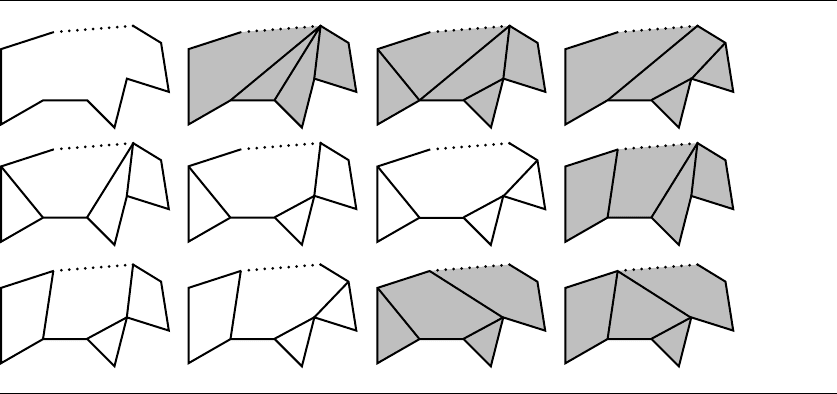
. Figure 13.76 shows an original polygon (upper left) and 11 minimum

convex decompositions. The narrowest pairs are shaded in gray. As it turns out, the

angular order of diagonals d

through d

, counterclockwise about a vertex V

, is the

same as the order of the vertices V

through V

, counterclockwise about the poly-

gon. A consequence of this observation is that narrowest pairs for the subproblem

can be tested for by just comparing indices of the associated pairs. Any associated

pair [a

, b

] of a potential decomposition is discarded whenever another associated

pair [a

, b

] with smaller indices is encountered; if a

≤ a

, it must also be the case

that b

≤ b

. As narrowest pairs for the subproblem for P

are computed, they are

pushed onto a stack so that the pairs from the bottom to the top of the stack are in

counterclockwise order about vertices V

and V

. The stack for the polygon in Fig-

ure 13.76 will contain [1, 3], [3, 4], and [6, 8], the last pair being the top of the stack.

The diagonals d

and d

thereby form the narrowest pair that is furthest counter-

clockwise.

Another key idea involves canonical triangulations of the convex polygons in the

decomposition. Each triangulation of a convex polygon is a triangle fan where the

base vertex of the fan is a reﬂex vertex of that convex polygon. Figure 13.77 illustrates

the canonical triangulations. The polygon of the ﬁgure is from Keil and Snoeyink

(1998), but with the vertices labeled differently to meet the constraint in the paper

that V

is a reﬂex vertex. The reﬂex vertex used as the base vertex of a fan has the

smallest index of all reﬂex vertices in the convex polygon for which the fan is con-

structed. Keil and Snoeyink mention the following observations. In a canonical tri-

angulation of the original polygon P , each diagonal d

with i<ksatisﬁes three

conditions with respect to subpolygon P

1. The diagonals with end points in P

deﬁne a canonical triangulation of P

2. If V

is a reﬂex vertex of P , then for the triangle V

, V

with i<j<k, either

j = k −1ord

is a diagonal used in the convex decomposition.

3. If V

is not a reﬂex vertex of P , then V

is a reﬂex vertex. For the triangle

V

, V

with i<j<k, either j =i +1ord

is a diagonal used in the convex

decomposition.

13.9 Polygon Partitioning 793

1, 3 1, 3 1, 3

3, 41, 81, 61, 4

3, 6 3, 8

6, 8 6, 8

Figure 13.76 Original polygon (upper left) and 11 minimum convex decompositions, with the nar-

rowest pairs shaded in gray. A dotted line indicates that the edge of the polygon is treated

instead as a diagonal.

In Figure 13.77, consider subpolygon P

9,11

so that i = 9 and k =11. The vertex

is reﬂex, so condition 2 applies. Triangle V

, V

 is in the canonical trian-

gulation of P and has j = 10 = k −1. In subpolygon P

16,23

, i = 16 and k = 23. The

vertex V

is reﬂex, so condition 2 applies. Triangle V

, V

 is in the canonical

triangulation of P , but j =17 =22 =k −1. However, d

17,23

is a diagonal used in the

convex decomposition. Consider subpolygon P

5,9

,soi = 5 and k =9. The vertex V

is not a reﬂex vertex, but V

is. Triangle V

, V

 is in the canonical triangulation

of P and has j = 6 = i + 1.

The minimum convex decompositions of P

are constructed by considering

which vertices V

form a canonical triangle with diagonal d

and whether diago-

nals d

and d

either are part of the decompositions of P

and P

or are just part

of the canonical triangulation. Putting this all together, the algorithm is to exam-

ine the canonical triangulations of the minimum decompositions of P

that have

narrowest pairs. The algorithm associates with each subpolygon P

a stack S

that

stores the narrowest pairs for P

in increasing order and a stack T

that stores these

pairs in decreasing order. An invariant of the algorithm is that when analyzing P

each subproblem P

smaller than P

has all its narrowest pairs stored in its corre-

sponding stacks. Only one of the two stacks for a subproblem is used at a time, so

both can be overlaid in the same memory. The data structure to use for S

is there-

fore a “double-ended stack.” Operations on S

are applied at one end of the storage,

whereas operations on T

are applied at the other end.