Schneider P., Eberly D.H. Geometric Tools for Computer Graphics

Подождите немного. Документ загружается.

804 Chapter 13 Computational Geometry Topics

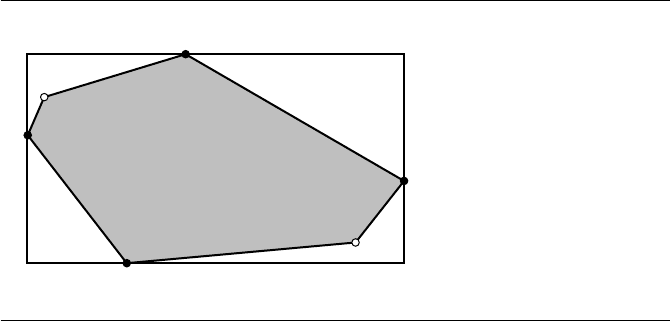
Figure 13.79 Purported minimum-area rectangle that has no coincident polygon edges.

Proof of Edge Containment

The proof of edge containment is by contradiction. Suppose that in fact no edge of

the convex polygon is contained by an edge of the minimum-area rectangle. The

rectangle must be supported by two, three, or four vertices of the convex polygon.

Figure 13.79 illustrates the case of four supporting vertices. The supporting vertices

are drawn in black and labeled V

through V

. Other polygon vertices are white. For

the sake of argument, rotate the convex polygon so that the axes of this rectangle are

(1, 0) and (0, 1) as shown in the ﬁgure.

Deﬁne u

(θ) = (cos θ, sin θ) and u

(θ) = (− sin θ ,cosθ). There exists a value

ε>0 such that the V

are always the supporting vertices of the bounding rectangle

with axes u

(θ) and u

(θ) for all angles θ satisfying the condition |θ | <= ε.To

compute the bounding rectangle area, the supporting vertices are projected onto the

axis lines V

+ s u

(θ) and V

+ t u

(θ). The intervals of projection are [0, s

] and

, t

], w he re s

=u

(θ) ·(V

−V

), t

=u

(θ) ·(V

−V

), and t

=u

(θ) ·(V

−V

Deﬁne



=(x

, y

) = V

−V

and



=(x

, y

) = V

−V

. From Figure 13.79 it

is clear that x

> 0 and y

> 0. The area of the rectangle for |θ|≤ε is

A(θ) = s

− t

) = [



·u

(θ)][



·u

(θ)]

In particular, A(0) =x

> 0.

Since A(θ) is differentiable on its domain and since A(0) is assumed to be the

global minimum, it must be that A



(0) = 0. Generally,



(θ) = [



·u

(θ)][



·u



(θ)] + [



·u



(θ)][



·u

(θ)]

=−[



·u

(θ)][



·u

(θ)] + [



·u

(θ)][



·u

(θ)]

13.11 Minimum Bounds for Point Sets 805

Therefore, 0 = A



(0) =−x

+ y

,orx

= y

. Since x

> 0 and y

> 0, it

must be that Sign(x

) = Sign(y

). Moreover, since A(0) is assumed to be the global

minimum, it must be that A



(0) ≥ 0. Generally,



(θ) =−[



·u

(θ)][



·u



(θ)] − [



·u



(θ)][



·u

(θ)]

+ [



·u

(θ)][



·u



(θ)] + [



·u



(θ)][



·u

(θ)]

=−[



·u

(θ)][



·u

(θ)] − [



·u

(θ)][



·u

(θ)]

− [



·u

(θ)][



·u

(θ)] − [



·u

(θ)][



·u

(θ)]

=−2



[



·u

(θ)][



·u

(θ)] + [



·u

(θ)][



·u

(θ)]



In particular, A



(0) =−2(x

+ x

) ≥ 0. However, note that x

> 0 since

A(0)>0 and x

> 0 since Sign(x

) = Sign(y

), which implies that A



(0)<0, a

contradiction.

An Implementation

Since the minimum-area rectangle must contain an edge, a simple implementation

just iterates over the edges of the convex hull. For each edge, the corresponding

smallest rectangle for the orientation deﬁned by the edge is computed. The minimum

area of all these rectangles is computed. The pseudocode for the algorithm is

ordered vertices P[0] through P[N - 1];

define P[N] = P[0];

minimumArea = infinity;

for (i = 1; i <= N; i++) {

U0 = P[i] - P[i - 1];

U1 = (-U0.x, U0.y);

s0=t0=s1=t1=0;

for(j=1;j<N;j++) {

D = P[j] - P[0];

test = Dot(U0, D);

if (test < s0) s0 = test; else if (test > s1) s1 = test;

test = Dot(U1, D);

if (test < t0) t0 = test; else if (test > t1) t1 = test;

}

area = (s1 - s0) * (t1 - t0);

if (area < minimumArea)

minimumArea = area;

}

806 Chapter 13 Computational Geometry Topics

This algorithm is O(n

) because of the double loops, each iterating over n items.

A better algorithm is considered in the next section and is based on an idea called the

rotating calipers method.

Rotating Calipers

The rotating calipers method is the idea used in the dissertation of Michael Shamos

(1978), a work that is considered to be the origin of the area of computational geom-

etry. The algorithm in that dissertation uses the method for computing the diameter

ofaconvexpolygoninO(n) time. Godfreid Toussaint coined the phrase “rotating

calipers” since the method resembles rotating a pair of calipers around the polygon.

The method is quite useful in solving other problems. Among those are computing

the minimum and maximum distances between two convex polygons, onion trian-

gulations (useful for triangulating point sets that occur on various contour lines for a

function f(x, y)), merging convex hulls, intersecting convex polygons, and comput-

ing the Minkowski sum/difference of two convex polygons (compare with the GJK

algorithm discussed in Section 6.10 of this book). These and more algorithms are

summarized at the rotating calipers home page (Pirzadeh 1999).

The application of rotating calipers to ﬁnding the minimum-area rectangle con-

taining a convex polygon is quite simple. An initial edge of the polygon is selected.

The edge direction and a perpendicular direction are used to ﬁnd the smallest bound-

ing rectangle with that orientation. The vertices and edge supporting the rectangle are

tracked during the construction. The rectangle will be rotated an edge at a time. The

edge starting at a supporting vertex forms an angle with the box edge containing the

vertex. The box is rotated by the smallest angle of all supporting vertices. The new

supporting edge is not necessarily adjacent to the previous supporting edge. The box

size is updated in O(1) time for the new orientation. The polygon has n edgestobe

visited, and the update is O(1) for each rotation of the box, so the total algorithm

is O(n).

13.11.2 Minimum-Volume Box

Just as in the 2D problem, it is evident that the only points that need to be considered

are the vertices of the convex hull of the original point set. The problem is therefore

reduced to ﬁnding the minimum-volume oriented box that contains a convex poly-

hedron. O’Rourke (1985) shows that one box face must contain a polyhedron face

and another box face must contain a polyhedron edge or three box faces must each

contain a polyhedron edge. The ﬁrst case can be performed in O(n

) time, but the

second case is performed in O(n

) time, so the total algorithm is O(n

). To date there

appears to be no known algorithm with a smaller asymptotic run time. However, an

approximation of the minimum-volume box can be efﬁciently computed (Barequet

and Har-Peled 1999).

13.11 Minimum Bounds for Point Sets 807

The box calculation based on a box face containing a polyhedron face uses the

rotating calipers method. There are O(n) polyhedron faces to process, each taking

O(n) time for a total of O(n

) time, as mentioned in the last paragraph. Given the

polyhedron face, the projection of the polyhedron onto the plane of the face produces

aconvexpolygon.Ifn is an outer normal vector to that face, the edges and faces of the

polyhedron that project onto the polygon are the separators between the faces of the

polygon whose normals m satisfy n ·m>0 and those whose normals satisfy n ·m<0.

The projection of the box onto the plane is a rectangle. The rotating calipers method

is applied to ﬁnd the minimum-area rectangle containing the convex polygon. This

equates to ﬁnding the minimum-volume box for the specifed polyhedron face.

The case of three edges supporting the box is handled in a straightforward man-

ner by iterating over all combinations of three edges, a total of O(n

) possibilities. For

each combination of three edges that are mutually orthogonal, a minimum-volume

box of that orientation is constructed. The hope for reducing the asymptotic order

is that somehow the combinations of three mutually orthogonal edges can be found

during the O(n

) processing of polyhedron faces.

The minimum-volume box for the polyhedron is chosen as the minimum of all

boxes constructed from faces and from edge combinations.

13.11.3 Minimum-Area Circle

An O(n) method for ﬁnding some bounding circle is to compute the minimum-area

axis-aligned rectangle that contains the points, then choose a circle that circumscribes

the rectangle. In most cases this circle is not the minimum-area circle containing the

points. In fact, sometimes the input points are all strictly interior to the circle. For

example, this situation occurs for the points {(±2, 0), (0, ±1)}. The bounding circle

is centered at (0, 0) and has radius

√

5. The maximum distance from the origin to an

input point is 2. Many applications require a better ﬁt than this.

A support point for a bounding circle is an input point that lies exactly on the

circle. The minimum-area circle containing the points clearly must be supported by

at least two input points; otherwise the purported circle could be shrunk in size until

it does touch another input point. Even though the point set could have more than

two input points, the minimum-area circle might only have two supporting points.

For example, the points {(−1, 0), (0, 0), (1, 0)}are collinear. The minimum-area circle

containing them has center (0, 0) and radius 1. The supporting points are (±1, 0).

In other examples, the number of supporting points is three. It is possible for the

number of input points exactly on the minimum-area circle to be four or more, but

only three are necessary since three noncollinear points uniquely determine the circle

(see Section 13.10).

Since at least two input points must be on the circle, it is tempting to assume

that those two points must be the ones farthest apart. This is not the case based

on the following counterexample. Let the input points be {(1, 0), (−1/2,

√

3/2),

(−1/2, −

√

3/2), (−3/4, 0)}. The points form a convex quadrilateral. The ﬁrst three

808 Chapter 13 Computational Geometry Topics

points form an equilateral triangle, the common length of the sides being

√

3. The

distance from (1, 0) to (−3/4, 0) is 7/4 >

√

3. Therefore, (1, 0) and (−3/4, 0) form

the most separated pair of input points. The minimum-area bounding circle is the

one containing the equilateral triangle and has center (0, 0) and radius 1. The circle

containing (1, 0), (−1/2,

√

3/2), and (−3/4, 0) has center (1/8,

√

3/8) and radius

√

13/4 < 1, but (−1/2, −

√

3/2) is not in that circle. The circle with antipodal points

(−3/4, 0) and (1, 0) has center (1/8, 0) and radius 7/8, but (−1/2, ±

√

3/2) are not

in that circle since the distance from those points to the circle center is approximately

1.068 > 7/8.

An exhaustive approach will produce the answer, but is slow. All triples of points

are analyzed. The minimum-area circle containing the three points is either the cir-

cumscribed circle or a circle for which two of the three points are antipodal. This is

particularly the case when the three points are collinear. The bounding circle of min-

imum radius in this process is tracked during the analysis. At the end, we have the

minimum-area circle for the input set. The algorithm is O(n

A more efﬁcient approach is to grow a circle to contain the points. The initial circle

is the one that contains the ﬁrst two input points. Each additional point is tested for

inclusion in that circle. If all are contained, with some possibly on the circle itself,

the initial circle is the one of minimum area. We are not usually so lucky to have this

happen. More likely is that one of the remaining points Q is outside the initial circle.

If this happens, the initial circle was not large enough and must be grown to include

Q.Infact,Q will be used as a supporting point for this new circle. A problem is

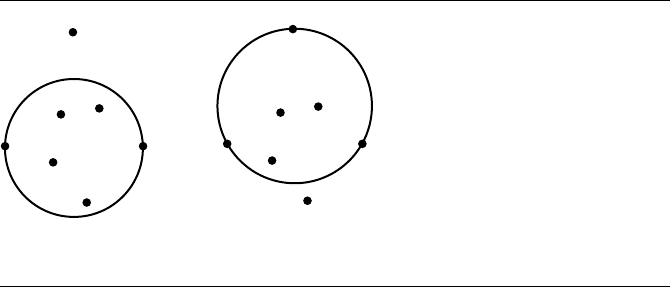
that many point-in-circle tests were performed before Q was encountered (see Figure

13.80). When the initial circle is modiﬁed to a new circle, points in the initial circle

might not be in the modiﬁed one. Effectively, the algorithm must start over, and all

the points have to be tested for containment in the new circle.

If the initial circle is the minimum-area circle, that was determined by testing n −

2 = O(n) points. If only m restarts are needed and m is effectively a small constant

compared to n, then the algorithm is O(n).However,ifm is comparable in size to

n, the asymptotic behavior is worse than O(n). To see this, consider the points on

a hemicircle, P

= (cos θ

, sin θ

),whereθ

= π i/(n − 1) for 0 ≤ i<n. The initial

bounding circle is supported by P

and P

. The next point P

is outside that circle,

so the algorithm is restarted. The new circle is supported by P

and P

. The point P

is inside this circle, but P

is not. At the ith iteration, the current bounding circle is

supported by P

and P

, points P

for 0 <j<iare inside the circle, but P

i+1

is not.

That is, the algorithm must restart each time. The ith iteration requires i point-in-

circle tests. The minimum-area circle is only known once you reach point P

n−1

, and

in fact all input points are on the circle. The total number of point-in-circle tests is



n−1

i=1

= n(n − 1)/2 = O(n

). More complicated examples of this type even lead to

O(n

) behavior, just like the exhaustive approach.

Taking a closer look at the hemicircle example, suppose that instead of processing

the points in the order given, the points are randomly permuted, then processed. For

the sake of argument, let P

always be a supporting point. If the second point in the

permuted set is P

,wherej is nearly n − 1, the initial circle is quite large. In the

13.11 Minimum Bounds for Point Sets 809

(a) (b)

Figure 13.80 (a) Current bounding circle and a point that is outside the circle, causing the circle

to grow. (b) The new bounding circle, but a point inside the old circle is now outside

the new circle, causing a restart of the algorithm.

ordered case, it took j iterations to get to this circle. In the permuted case, we have

saved a lot of time. Another point, P

, processed in the permuted case that causes a

restart hopefully will have index k that is larger than j + 1, again skipping a couple

of iterations that were performed in the ordered case. The hope is that the number of

restarts, m, is effectively a small constant compared to n, in which case the algorithm

is O(n).

The formalization of this approach is found in Welzl (1991) and is one of a class

of algorithms called randomized linear algorithms. The permutation of the input data

has expected time behavior of O(n). This does not mean that all input data sets will

run in this time. It is possible, although not highly probable, that the permutation

of the input points leads to an ordering that does cause superlinear behavior. For

example, the permutation for the hemicircle problem might turn out to be the iden-

tity, in which case that example runs in O(n

) time. Assuming uniform distribution

of the permutations, the probability that the permutation is the identity in that ex-

ample is 1/n!, a very small number for large n. Of course, other permutations that

result in only a couple of transpositions will cause similar slow construction of the

circle, but as noted, the expected time is O(n). The concept applies to higher di-

mensions, of which the 3D problem is discussed next. In d-dimensional space, the

expected number of point-in-circle tests is n(d +1)!. That is, the asymptotic constant

is approximately (d + 1)!.

The recursive formulation of the algorithm is

Circle MinimumAreaCircle(PointSet Input, PointSet Support)

{

if (Input is not empty) {

P = GetRandomElementOf(Input);

Input’ = Input - {P}; // remove P from Input

810 Chapter 13 Computational Geometry Topics

C = MinimumAreaCircle(Input’, Support);

if (P is inside C) {

return C;

} else {

Support’ = Support + {P}’; // add P to Support

return MinimumAreaCircle(Input’, Support’);

}

} else {

return CircleOf(Support);

}

A nonrecursive formulation is

Circle MinimumAreaCircle(int N, Point P[N])

{

randomly permute P[0] through P[N - 1];

C = ExactCircle1(P[0]); // center P[0], radius 0

Support = { P[0] };

i=1;

while (i < N) {

if (P[i] is not an element of Support) {

if (P[i] is not contained by C) {

C = Update(P[i], Support);

i = 0; // restart the algorithm for the new circle

continue;

}

i++;

}

return C;

}

The Update function has the job of adding P[i] to the support set Support and

removing other elements of

Support that are no longer supporting points because of

the addition of

P. Beware: this function must be implemented with care when us-

ing ﬂoating-point arithmetic. The problem is that old supporting points are tested

for containment in various combinations of the supporting points and

P[i]. One of

those combinations must theoretically contain all the old supporting points. How-

ever, numerical round-off errors can cause a situation where none of the combina-

tions appears to contain all the points. Even with the introduction of a numerical

epsilon for point-in-circle tests, you can still run into problems. One solution is to

13.11 Minimum Bounds for Point Sets 811

trap the case when no circle appears to contain all the support points and use the cir-

cle for which the offending point outside the circle is closest to that circle, compared

to the same offending points for the other circles. The construction of the circles

for the various combinations relies on the existence of functions that calculate the

minimum-area circle of two points and of three points. An implementation must, of

course, provide these.

Another potential problem with ﬂoating point is that the update call always as-

signs a new circle to the current minimum-area circle

C. It is possible to encounter a

situation, when using ﬂoating-point arithmetic, where the loop becomes inﬁnite be-

cause of a cycle of two points in the support set that are alternately swapped out. The

problem is that, in theory, the circle returned by the update has larger radius than

the current circle

C. However, numerical round-off errors cause the radius of the re-

turned circle to be smaller, thus leading to the inﬁnite loop. The solution is to replace

the block containing the update by

Circle tmp = Update(P[i], Support);

if (tmp.radius > C.radius) {

C = tmp;

i=0;

continue;

}

Other concerns that an implementation must address include handling du-

plicate input points and points that are distinct but numerically nearly identical.

The construction of circles containing three noncollinear points shows up in an

implementation—the circumscribed-circle-about-triangle problem that uses a lin-

ear system solver to ﬁnd the center and radius. The determinant of the system can be

close to zero if three points are nearly collinear, so the implementation should handle

this properly by detecting this and switching to computing the minimum-area circle

containing two points (discarding the correct point from the nearly collinear points).

13.11.4 Minimum-Volume Sphere

The problem of constructing the minimum-volume sphere that contains a set of in-

put points is handled in the same manner as the 2D problem of ﬁnding a minimum-

area circle containing a set of points. We recommend reading the previous section on

the circle problem to understand the intuition and ideas.

A popular misconception among novice graphics programmers is that the small-

est sphere containing the input points can be constructed by selecting the sphere

center to be the average of the input points, then determining the input point far-

thest from the center to obtain the sphere radius. Although this is a viable and easily

implementable algorithm for computing a bounding sphere, the resulting sphere is

not necessarily the one of minimum volume.

812 Chapter 13 Computational Geometry Topics

The randomized algorithm in Welzl (1991) applies in general dimensions, so in

3D in particular. The recursive formulation is identical to the 2D formulation, but

the function computes spheres instead of circles.

Sphere MinimumVolumeSphere(PointSet Input, PointSet Support)

{

if (Input is not empty) {

P = GetRandomElementOf(Input);

Input’ = Input - {P}; // remove P from Input

S = MinimumVolumeSphere(Input’, Support);

if (P is inside S) {

return S;

} else {

Support’ = Support + {P}’; // add P to Support

return MinimumVolumeSphere(Input’, Support’);

}

} else {

return SphereOf(Support);

}

The nonrecursive formulation is also similar to the one in two dimensions:

Sphere MinimumVolumeSphere(int N, Point P[N])

{

randomly permute P[0] through P[N - 1];

S = ExactCircle1(P[0]); // center P[0], radius 0

Support = { P[0] };

i=1;

while (i < N) {

if (P[i] is not an element of Support) {

if (P[i] is not contained by S) {

S = Update(P[i], Support);

i = 0; // restart the algorithm for the new sphere

continue;

}

i++;

}

return S;

}

13.11 Minimum Bounds for Point Sets 813

The same numerical concerns that arise in the two-dimensional problem must be

addressed in the three-dimensional one. See the end of Section 13.11.3 for what those

concerns are and how to deal with them in an implementation.

13.11.5 Miscellaneous

Other types of minimum-area or volume-bounding regions are sometimes called for

in applications. Generally, the construction of such bounds can be quite challenging

from the point of view of both algorithm development and implementation.

Minimum-Area Ellipse

As an example, consider the problem of ﬁnding the minimum-area ellipse that con-

tains a set of points. An extension of the minimum-area circle algorithm is immediate

(Gaertner and Schoenherr 1998). In the circle problem, the update of the supporting

set required constructing the minimum circle for pairs and triples of support points.

These are referred to as small problems whose solutions are used to determine the

original large problem with n points. The small problems for the ellipse bounding

involves computing minimum-area ellipses for three, four, or ﬁve points. For three

noncollinear points P

,0≤i ≤2, the equation of the minimum-area ellipse that con-

tains the points is (X − C)

M(X − C) = 2, where

C =



i=0

the average of the points, and M is the 2 ×2 matrix whose inverse is

−1



i=0

− C)(P

− C)

For ﬁve points that form a convex polygon, the minimum-area ellipse is the exact

ﬁtting ellipse for the ﬁve points. The general quadratic equation that represents either

an ellipse, hyperbola, or parabola is x

+ axy + by

+ cx + dy + e = 0. The ﬁve

coefﬁcients are computed by creating ﬁve linear equations from the general quadratic

equation—a system that is easy to solve.

The harder problem is computing the minimum-area ellipse containing four

points that form a convex quadrilateral. To see the complexity of the problem,

consider the special case when the points are (0, 0), (1, 0), (0, 1), and (u, v) with

u>0, v>0, and u + v>1. The quadratic equation that contains the four points

as solutions is x

+ bxy + cy

− x − cy = 0, where c>0, b

< 4c, and b = (1 −

u)/v +c(1 −v)/u. The independent variable is c, so there are inﬁnitely many ellipses