Schneider P., Eberly D.H. Geometric Tools for Computer Graphics

Подождите немного. Документ загружается.

854 Appendix A Numerical Methods

a full basis of eigenvectors. The standard approach is to apply orthogonal transfor-

mations, called Householder transformations, to reduce A to a tridiagonal matrix. The

QR algorithm is applied iteratively to reduce the tridiagonal matrix to a diagonal one.

Press et al. (1998) advise using a QL algorithm with implicit shifting to be as robust

as possible. For n = 3, the problem can be solved by simply computing the roots of

det(A − λI) = 0. The numerical issues many times can be avoided since the end re-

sult is some visual presentation of data where the numerical error is not as important

as for applications that require high precision.

Solving the eigensystem for an n × n symmetric matrix A implies a factorization

for A.Letλ

through λ

be the distinct eigenvalues for A. The dimension of the

eigenspace for λ

is d

≥ 1 and



i=1

= n. That is, we can choose an orthonormal

setofvectors ˆq

,1≤ i ≤ n, that is the union of orthonormal sets for each of the

eigenspaces. Because these vectors are themselves eigenvectors, A ˆq

= λ



ˆq

,where



is the eigenvalue corresponding to the eigenspace in which ˆq

lives. Deﬁne the

diagonal matrix  = Diag{λ



, ..., λ



}. Deﬁne Q to be the matrix whose columns

are the ˆq

. The eigenequations are jointly written as AQ =Q,orA =QQ

. This

last equation is called an eigendecomposition of A.

A.3.4 Polar Decomposition

Suppose an object has been transformed by translations, rotations, and nonuniform

scalings through a sequence of homogeneous matrix operations. The total transfor-

mation is just the product of the individual transformations. A common question

asked by many practitioners is how to extract from the total transformation its trans-

lation, rotation, and nonuniform scales. The question is ill-posed, but the motivation

for asking it is as follows. Suppose that the homogeneous transformations are of the

block form







where



isa3× 1 translation vector;



isa1× 3zerovector;S

is the nonuniform

scaling matrix, a 3 ×3 diagonal matrix whose diagonal entries are positive; and R

a3× 3 rotation matrix. Suppose that n such transformations are applied to an object

and the ﬁnal transformation is H = H

n−1

···H

. What the question is aimed

at is factoring

H =







A.3 Matrix Decompositions 855

Clearly the translation vector is an easy term to select! However, the scaling and

rotation are problematic. Consider just the product of two such homogeneous trans-

formations























The total translation is



t = R



. The total scale-rotation component is

. In the special case that both S

and S

represent uniform scales, that is,

= σ

I for i = 1, 2 and where I is the identity matrix, we can determine R and S

uniquely by

= R

I =R

= R

(σ

)

The ability to commute σ

and R

is just a property of scalar multiplication of a

matrix. The ﬁnal selection is S =σ

I, another uniform scaling, and R = R

,aro-

tation since it is the product of two rotations. In this special case of two homogeneous

terms, if S

is a uniform scale matrix, then S =S

and R =R

. But the complica-

tion is when S

is nonuniform. Generally, if D

is a diagonal matrix for which at least

two diagonal entries are different, and if R

is a rotation matrix, it is not possible to

ﬁnd a diagonal matrix D

for which R

= D

with R

a rotation matrix. Gener-

ally, if the transformation system of a graphics engine allows nonuniform scaling, the

complication arises.

The intuitive problem is that the nonuniform scales are applied along speciﬁc

axes, so the orientation of those axes is an important issue. In 2D consider transform-

ing the circle x

=1 by rotations and nonuniform scaling. Figure A.1 illustrates

the problem. Observe that if we allow scaling along a different set of coordinate axes,

in this case the axes (1, 1)/

√

2 and (−1, 1)/

√

2, we can force the circle in the bottom

sequence to stretch to the ﬁnal ellipse in the top sequence. The scale 2 must be applied

along the direction (1, 1)/

√

This motivates what is called the polar decomposition. A nonuniform scale in

a particular coordinate system is obtained by rotating that system to the standard

coordinate system, applying the scaling in the standard system, then rotating back to

the original system. If R represents the rotation from the speciﬁed coordinate system

to the standard coordinate system and if D is the diagonal nonuniform scaling matrix

in the standard coordinate system, then the scaling in the speciﬁed coordinate system

is S = R

DR. This just states mathematically what we said in words. The matrix S is

necessarily symmetric.

Given a matrix A, the polar decomposition is A =QS,whereQ is an orthogonal

matrix and S is a symmetric matrix. In the application mentioned previously, the

matrix of interest is A =R

. It is generally not possible to factor A =RS,where

R is a rotation and S is diagonal. The polar decomposition is always possible. The

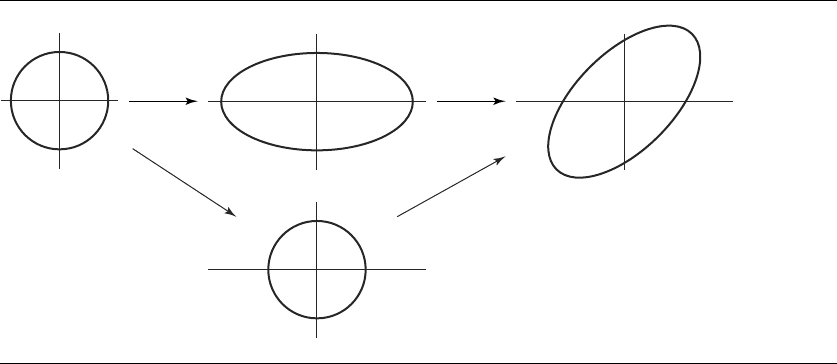
856 Appendix A Numerical Methods

Scale Rotate

Rotate Scale?

Figure A.1

The top sequence shows a nonuniform scale (x, y) → (2x, y) applied ﬁrst, a counterclock-

wise rotation by π/4 second. The bottom sequence shows a rotation by any angle (the circle

is invariant under rotations), but clearly there is no nonuniform scaling along coordinate

axes that can force the circle to become the ellipse of the top sequence.

symmetric matrix S represents scaling in some coordinate system. If that coordinate

system is the standard one (directions (1, 0, 0), (0, 1, 0), (0, 0, 1)), then S is diagonal.

Observe that A

A = S

QS = S

S = S

, where the second equality is true since

Q is orthogonal and the third equality is true since S is symmetric. The matrix

A is positive semideﬁnite since x

B x =x

Ax =Ax

≥ 0. Therefore, S

A must have a positive semideﬁnite square root (Horn and Johnson 1985). The

square root can be constructed by an eigendecomposition S

= R

DR,whereR is

orthogonal and D is diagonal with nonnegative diagonal entries. A square root is

S =R

1/2

R,whereD

1/2

is the diagonal matrix whose diagonal entries are the square

roots of the diagonal entries of D.IfS is invertible (the scalings are all positive), Q is

obtained by Q = AS

−1

.IfS is not invertible, then A itself is not invertible. The polar

decomposition for such a matrix can be obtained by singular value decomposition,

which is discussed in the next section. In typical graphics applications, A is in fact

invertible.

Construction of S as shown in the previous paragraph is certainly a valid way

of obtaining the decomposition. If a standard numerical eigensystem solver is used,

the construction is iterative. An alternative method that is also iterative is presented

in Heckbert (1994) by Ken Shoemake and constructs Q ﬁrst. Once Q is known, S =

A. The initial iterate is Q

= A. The next iterates are generated by Q

i+1

= (Q

−T

)/2. The iteration terminates when the change between consecutive iterates is

sufﬁciently small.

A.4 Representations of 3D Rotations 857

A.3.5 Singular Value Decomposition

An eigendecomposition naturally factors a symmetric matrix A into A = R

DR,

where R is orthogonal and D is diagonal. For a nonsymmetric matrix, this type

of factorization is not always possible. What is possible is a factorization called the

singular value decomposition. Any matrix A can be factored into A = LSR

,where

L and R are both orthogonal matrices and where S is diagonal with nonnegative

diagonal entries (for a proof, see Horn and Johnson 1985). The diagonal entries of

S are the eigenvalues of AA

, the columns of L are eigenvectors of AA

, and the

columns of R are eigenvectors of A

A arranged in the same order relative to the

eigenvalues as that for the columns of L. As a result, an eigendecomposition of AA

and A

A will lead to the singular value decomposition. But as it turns out, there are

more efﬁcient numerical methods for the decomposition, for example, in Golub and

Van Loan (1993).

A.4 Representations of 3D Rotations

This section discusses three different schemes for representing 3D rotations—matrix,

axis-angle, and quaternion—and how to convert between schemes.

A.4.1 Matrix Representation

A 2D rotation is a tranformation of the form







cos(θ) − sin(θ )

sin(θ) cos(θ )





where θ is the angle of rotation. A 3D rotation is a 2D rotation that is applied within

a speciﬁed plane that contains the origin. Such a rotation can be represented by a

3 ×3 rotation matrix R =[ˆr

ˆr

]whose columns ˆr

, ˆr

, and ˆr

form a right-handed

orthonormal set. That is, ˆr

=ˆr

=1, ˆr

·ˆr

=ˆr

·ˆr

=ˆr

·ˆr

= 0, and

ˆr

·ˆr

×ˆr

= 1. The columns of the matrix correspond to the ﬁnal rotated values of

the standard basis vectors (1, 0, 0), (0, 1, 0), and (0, 0, 1), in that order. Given a 3 ×1

vector x =[x

] and 3 × 3 rotation matrix R = [r

], the rotated vector is

R x =







j=0





(A.3)

858 Appendix A Numerical Methods

A.4.2 Axis-Angle Representation

If the plane of rotation has unit-length normal ˆw, then the axis-angle representation of

the rotation is the pair ˆw, θ. The direction of rotation is chosen so that as you look

down on the plane from the side to which ˆw points, the rotation is counterclockwise

about the origin for θ>0. This is the same convention used for a 2D rotation.

Axis-Angle to Matrix

If ˆu, ˆv, and ˆw form a right-handed orthonormal set, then any point can be repre-

sented as x = u

ˆu + v

ˆv +w

ˆw; see Section 9.2.2 on coordinate frames relative to a

plane. Rotation of x about the axis ˆw by the angle θ produces R x =u

ˆu +v

ˆv +w

ˆw.

Clearly from the geometry, w

=ˆw ·x. The other two components are changed

as if a 2D rotation has been applied to them, so u

= cos(θ )u

− sin(θ )v

and v

sin(θ)u

+ cos(θ )v

. Using the right-handedness of the orthonormal set, it is easily

shown that

ˆw ×x = u

ˆw ×ˆu + v

ˆw ×ˆv + w

ˆw ×ˆw =−v

ˆu + u

ˆv

and

ˆw × ( ˆw ×x) =−v

ˆw ×ˆu + u

ˆw ×ˆv =−u

ˆu − v

ˆw

Combining these in the form shown and using the relationship between u

, v

, and v

produces

(sin θ) ˆw ×x + (1 − cos θ) ˆw × ( ˆw ×x) = (−v

sin θ − u

(1 − cos θ))ˆu

+ (u

sin θ − v

(1 − cos θ))ˆv

= (u

− u

) ˆu + (v

− v

) ˆv

= R x −x

Therefore, the rotation of x given the axis ˆw and angle θ is

R x =x +(sin θ) ˆw ×x + (1 − cos θ) ˆw × ( ˆw ×x) (A.4)

This can also be written in matrix form by deﬁning the following, where ˆw =(a, b, c),

S =





0 −cb

c 0 −a

−ba 0





A.4 Representations of 3D Rotations 859

in which case

R = I +(sin θ)S +(1 −cos θ)S

and consequently Rx =x + (sin θ)Sx + (1 − cos θ)S

x.

Matrix to Axis-Angle

The inverse problem is to start with the rotation matrix and extract an angle and unit-

length axis. There are multiple solutions since −ˆw is a valid axis whenever ˆw is and

θ + 2πk is a valid solution whenever θ is. First, the trace ofamatrixisdeﬁnedtobe

the sum of the diagonal terms. Some algebra will show that cos θ =(Tr ac e(R) −1)/2,

in which case

θ = cos

−1

((Tr ac e(R) − 1)/2) ∈ [0, π] (A.5)

Also, it is easily shown that

R − R

= (2 sin θ)S (A.6)

where S is a skew-symmetric matrix. The constructions below are based on the cases

θ = 0, θ ∈ (0, π), and θ =π.

If θ = 0, then any unit-length direction vector for the axis is valid since there

is no rotation. If θ ∈ (0, π), Equation A.6 allows direct extraction of the axis,



d =

−r

, r

−r

, r

−r

) and ˆw =



d/



d.Ifθ = π , Equation A.6 does not help

with constructing the axis since R − R

= 0. In this case note that

R = I +2S







1 − 2(w

+ w

) 2w

1 − 2(w

+ w

) 2w

1 − 2(w

+ w

)







where ˆw = (w

, w

). The idea is to extract the maximum component of the

axis from the diagonal entries of the rotation matrix. If r

is maximum, then w

must be the largest component in magnitude. Compute 4w

= r

− r

+ 1

and select w

√

− r

+ 1/2. Consequently, w

= r

/(2w

) and w

/(2w

).Ifr

is maximum, then compute 4w

= r

− r

+ 1 and select

√

− r

+ 1/2. Consequently, w

/(2w

) and w

/(2w

). Fi-

nally, if r

is maximum, then compute 4w

= r

− r

+ 1 and select w

√

− r

+ 1/2. Consequently, w

= r

/(2w

) and w

= r

/(2w

860 Appendix A Numerical Methods

A.4.3 Quaternion Representation

A third representation involves unit quaternions. Only a summary is provided here.

Details of the relationship between rotations and quaternions can be found in Shoe-

make (1987) and Eberly (2000). A unit quaternion is denoted by q =w + xi + yj +

zk,wherew, x, y, and z are real numbers and where the 4-tuple (w, x, y, z) is unit

length. The set of unit quaternions is just the unit hypersphere in R

. The products

of i, j , and k are deﬁned by i

= j

= k

=−1, ij =−ji = k, jk =−kj = i, and

ki =−ik = j . Observe that the products are not commutative.Theproductoftwo

unit quaternions q

= w

+ x

i + y

j + z

k for n = 0, 1 is deﬁned by distributing

the product over the sums, keeping in mind that the order of operands is important:

= (w

− x

− y

− z

)

+ (w

+ x

+ y

− z

+ (w

− x

+ y

+ z

+ (w

+ x

− y

+ z

The conjugate of q is deﬁned by

∗

= w − xi − yj − zk

Observe that qq

∗

q =1 where the right-hand side 1 is the w-term of the quater-

nion, the x-, y-, and z-terms all being 0.

Axis-Angle to Quaternion

If ˆa =(x

, y

, z

) is the unit-length axis of rotation and if θ is the angle of rotation, a

quaternion q =w +xi +yj +zk that represents the rotation satisﬁes w =cos(θ/2),

x =x

sin(θ/2), y =y

sin(θ/2), and z = z

sin(θ/2).

Ifavectorv =(v

, v

) is represented as the quaternion v = v

i + v

j + v

and if q represents a rotation, then the rotated vector u is represented by quaternion

u = u

i +u

j + u

k,where

u = qvq

∗

(A.7)

It can be shown that the w-term of u must really be 0.

Quaternion to Axis-Angle

Let q = w +xi + yj + zk be a unit quaternion. If w=1, then the angle is θ = 0

and any unit-length direction vector for the axis will do since there is no rotation.

A.4 Representations of 3D Rotations 861

If w < 1, the angle is obtained as θ = 2cos

−1

(w), and the axis is computed as

ˆu = (x, y, z)/

√

1 − w

Quaternion to Matrix

Using the identities 2 sin

(θ/2) = 1 − cos(θ) and sin(θ) = 2 sin(θ/2) cos(θ/2),it

is easily shown that 2wx = (sin θ)w

,2wy = (sin θ)w

,2wz = (sin θ)w

,2x

(1 −cos θ)w

,2xy =(1 −cos θ)w

,2xz =(1 −cos θ)w

,2y

=(1 −cos θ)w

2yz = (1 − cos θ)w

, and 2z

= (1 − cos θ)w

. The right-hand sides of all these

equations are terms in the expression R = I + (sin θ)S + (1 − cos θ)S

. Replacing

them yields

R =





1 − 2y

− 2z

2xy + 2wz 2xz − 2wy

2xy − 2wz 1 − 2x

− 2z

2yz − 2wx

2xz + 2wy 2yz −2wx 1 − 2x

− 2y





(A.8)

Matrix to Quaternion

Earlier it was mentioned that cos θ = (Tr ac e(R) − 1)/2. Using the identity

2cos

(θ/2) = 1 + cos θ yields w

= cos

(θ/2) = (Tr ace (R) + 1)/4or|w|=

√

Tr ac e(R) + 1/2. If Trace(R)>0, then |w| > 1/2, so without loss of generality

choose w to be the positive square root, w =

√

Tr ac e(R) + 1/2. The identity R −

=(2 sin θ)S also yielded (r

−r

, r

−r

, r

−r

) =2 sin θ(w

, w

). Fi-

nally, identities derived earlier were 2xw = w

sin θ ,2yw = w

sin θ , and 2zw =

sin θ. Combining these leads to x = (r

− r

)/(4w), y = (r

− r

)/(4w), and

z = (r

− r

)/(4w).

If Trace(R) ≤ 0, then |w|≤1/2. The idea is to ﬁrst extract the largest one of x, y,

or z from the diagonal terms of the rotation R in Equation A.8. If r

is the maximum

diagonal term, then x is larger in magnitude than y or z. Some algebra shows that

= r

− r

+ 1, from which is chosen x =

√

− r

+ 1/2. Conse-

quently, w =(r

−r

)/(4x), y =(r

)/(4x), and z =(r

)/(4x).Ifr

the maximum diagonal term, then compute 4y

−r

+1and choose y =

√

− r

+ 1/2. Consequently, w = (r

− r

)/(4y), x = (r

+ r

)/(4y),

and z = (r

+ r

)/(4y). Finally, if r

is the maximum diagonal term, then com-

pute 4z

−r

+1 and choose z =

√

− r

+ 1/2. Consequently,

w = (r

− r

)/(4z), x =(r

+ r

)/(4z), and y =(r

+ r

)/(4z).

A.4.4 Performance Issues

A question asked quite often is, “What is the best representation to use for rotations?”

As with most computer science topics, there is no answer to this question, only trade-

862 Appendix A Numerical Methods

Table A.1 Comparison of memory usage.

Representation Floats Comments

Rotation matrix 9

Axis-angle 4 No precompute of sin θ or 1 − cos θ

Axis-angle 6 Precompute of sin θ and 1 − cos θ

Quaternion 4

offs to consider. In the discussion, the rotation matrix is R, the quaternion is q,

and the axis-angle pair is ( ˆa, θ). Various high-level operations are compared by a

count of low-level operations including multiplication (M), addition or subtraction

(A), division (D), and expensive math library function evaluations (F). In an actual

implementation, comparisons (C) should also be counted because they can be even

more expensive than multiplications and/or additions. Summary tables are provided

to allow you to quickly compare the performance.

Memory Usage

A rotation matrix requires 9 ﬂoats, a quaternion requires 4 ﬂoats, and an axis-angle

pair requires 4 ﬂoats, so clearly the rotation matrix will use more memory. Storing

only the angle in the axis-angle formulation is clearly not helpful when transform-

ing is required since you need to know the values of sin θ and 1 − cos θ. Evaluating

the trigonometric functions is quite expensive. It is better to precompute both quan-

tities and store them, so in fact an axis-angle pair will require 6 ﬂoats, making the

quaternion representation the cheapest in memory usage. Table A.1 is a summary

of the memory usage. The axis-angle count includes 3 ﬂoats for the axis, 1 ﬂoat for

the angle θ , and 2 ﬂoats for sin θ and 1 − cos θ . Without the precomputation of the

trigonometric functions, any operation requiring the function values will be quite

expensive.

Conversion Time

Applications using rotations invariably have to convert from one representation to

another, so it is useful to have measurements of costs for the conversions. The entities

involved are a rotation matrix R, an axis-angle pair ( ˆa, θ), and a quaternion q.Itis

assumed that the angle of rotation is in (0, π).

A.4 Representations of 3D Rotations 863

Axis-Angle to Matrix

Evaluation of σ = sin(θ) and γ = cos(θ ) requires two function calls. The term

1 − γ requires 1 addition. The skew-symmetric matrix S obtained from ˆa requires

no computation. The matrix S

requires 6 unique multiplications and 3 additions;

sign changes are not counted. The term (1 − γ)S

requires 6 unique multiplica-

tions. The term σ S requires 3 unique multiplications. Finally, the combination

R = I +σ S + (1 − γ)S

uses 9 additions. The total cost is 13A + 15M +2F .

Matrix to Axis-Angle

The extraction θ = cos

−1

((Tr ac e(R) − 1)/2) requires 3 additions, 1 multiplication,

and 1 function call. The vector



d =(r

−r

, r

−r

, r

−r

) requires 3 additions.

The normalized vector ˆa =



d/|



d| requires 6 multiplications, 2 additions, 1 division,

and 1 function call. The total cost is 8A + 7M + 1D + 2F .

Axis-Angle to Quaternion

Extracting θ = 2cos

−1

(w) requires 1 function call and 1 multiplication. Construct-

ing ˆa = (x, y, z)/

√

1 − w

requires 4 multiplications, 1 addition, 1 division, and 1

function call. The total cost is 1A + 5M + 1D + 2F .

Quaternion to Axis-Angle

Evaluation of θ/2 uses 1 multiplication. Evalution of σ =sin(θ/2) and w = cos(θ/2)

requires 2 function calls. The products (x, y, z) = σ ˆa require 3 multiplications. The

total cost is 4M +2F .

Quaternion to Matrix

The conversion requires 12 multiplications. The terms t

= 2x, t

= 2y, and t

2z are computed. From these the following terms are computed: t

= wt

, t

= wt

, t

= t

x, t

= xt

, t

= xt

, t

= t

y, t

= yt

, and t

= t

The rotation matrix entries require 12 additions: r

= 1 − t

− t

, r

= t

− t

= t

+ t

, r

= t

+ t

, r

= 1 − t

− t

, r

= t

− t

, r

= t

− t

= t

+ t

, and r

= 1 − t

− t

. The total cost is 12A + 12M.

Matrix to Quaternion

The conversion depends on the sign of the trace of R. Computing the trace τ =

Tr ac e(R) requires 2 additions. Suppose that τ>0 (this comparison is 1C in cost).

The calculation w =

√

τ + 1/2 requires 1 addition, 1 multiplication, and 1 function

call. The expression λ = 1/(4w) requires 1 multiplication and 1 division. The terms