Schneider P., Eberly D.H. Geometric Tools for Computer Graphics

Подождите немного. Документ загружается.

884 Appendix A Numerical Methods

For n = 3, if A = (a, b, c), then matrix M(A) is given by

M(A) = δ





100

010

001





−









i=1

− a)



i=1

− a)(y

− b)



i=1

− a)(z

− c)



i=1

− a)(y

− b)



i=1

− b)



i=1

− b)(z

− c)



i=1

− a)(z

− c)



i=1

− b)(z

− c)



i=1

− c)







where

δ =



i=1

− a)



i=1

− b)



i=1

− c)

A.7.3 Planar Fitting of Points (x, y, f (x, y))

The assumption is that the z-component of the data is functionally dependent on the

x- and y-components. Given a set of samples {(x

, y

, z

)}

i=1

, determine a, b, and c

so that the plane z = ax +by + c best ﬁts the samples in the sense that the sum of

the squared errors between the z

and the plane values ax

+ by

+ c is minimized.

Note that the error is measured only in the z-direction.

Deﬁne E(a, b, c) =



i=1

[(ax

+ by

+ c) − z

]

. This function is nonnegative,

and its graph is a hyperparaboloid whose vertex occurs when the gradient satisﬁes



∇E =(0, 0, 0). This leads to a system of three linear equations in a, b, and c that can

be easily solved. Precisely,

(0, 0, 0) =



∇E =2



i=1

[(ax

+ by

+ c) −z

](x

, y

,1)

and so









i=1



i=1



i=1



i=1



i=1



i=1



i=1



i=1



i=1























i=1



i=1



i=1







The solution provides the least squares solution z = ax + by + c.

A.7.4 Hyperplanar Fitting of Points Using Orthogonal

Regression

It is also possible to ﬁt a plane using least squares where the errors are measured

orthogonally to the proposed plane rather than measured vertically. The following

A.7 Least Squares Fitting 885

argument holds for sample points and hyperplanes in n dimensions. Let the hyper-

plane be ˆn · (X − A) = 0, where ˆn is a unit-length normal to the hyperplane and A

is a point on the hyperplane. Deﬁne X

to be the sample points; then

= A + λ

ˆn + p

ˆn

⊥

where λ

=ˆn · (X

− A) and ˆn

⊥

is some unit-length vector perpendicular to ˆn with

appropriate coefﬁcient p

. Deﬁne y

= X

− A. The vector from X

to its projection

onto the hyperplane is λ

ˆn. The squared length of this vector is λ

=( ˆn ·y

)

. The en-

ergy function for the least squares minimization is E(A, ˆn) =



i=1

. Two alternate

forms for this function are

E(A, ˆn) =



i=1



y

ˆn ˆn

y



and

E(A, ˆn) =ˆn





i=1

y



ˆn =ˆn

M(A) ˆn

Using the ﬁrst form of E in the previous equation, take the derivative with respect to

A to get

∂E

∂A

=−2

ˆn ˆn



i=1

y

This partial derivative is zero whenever



i=1

y

= 0, in which case A = (1/m)



i=1

(the average of the sample points).

Given A, the matrix M(A) is determined in the second form of the energy func-

tion. The quantity ˆn

M(A) ˆn is a quadratic form whose minimum is the smallest

eigenvalue of M(A). This can be found by standard eigensystem solvers. A corre-

sponding unit-length eigenvector ˆn completes our construction of the least squares

hyperplane.

For n = 3, if A = (a, b, c), then matrix M(A) is given by

M(A) =









i=1

− a)



i=1

− a)(y

− b)



i=1

− a)(z

− c)



i=1

− a)(y

− b)



i=1

− b)



i=1

− b)(z

− c)



i=1

− a)(z

− c)



i=1

− b)(z

− c)



i=1

− c)







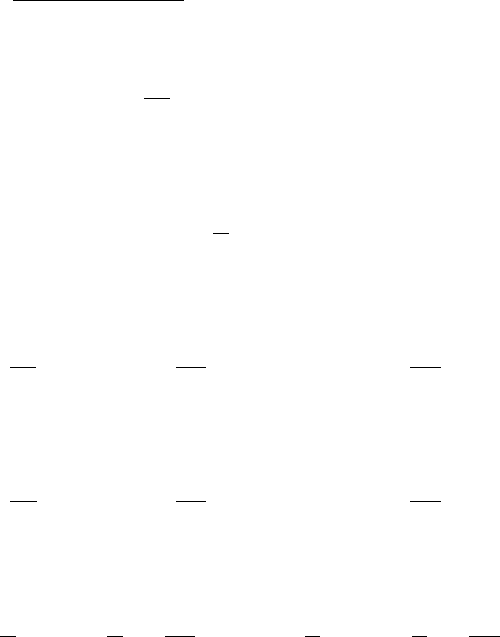
886 Appendix A Numerical Methods

A.7.5 Fitting a Circle to 2D Points

Given a set of points {(x

, y

)}

i=1

, m ≥3, ﬁt them with a circle (x − a)

+(y −b)

,where(a, b) is the circle center and r is the circle radius. An assumption of this

algorithm is that not all the points are collinear. The energy function to be minimized

E(a, b, r) =



i=1

− r)

where L

− a)

+ (y

− b)

. Take the partial derivative with respect to r to

obtain

∂E

∂r

=−2



i=1

− r)

Setting equal to zero yields

r =



i=1

Take the partial derivative with respect to a to obtain

∂E

∂a

= 2



i=1

− r)

∂L

∂a

=−2



i=1



− a) + r

∂L

∂a



and take the partial derivative with respect to b to obtain

∂E

∂b

= 2



i=1

− r)

∂L

∂b

=−2



i=1



− b) +r

∂L

∂b



Setting these two derivatives equal to zero yields

a =



i=1

+ r



i=1

∂L

∂a

and b =



i=1

+ r



i=1

∂L

∂b

Replacing r by its equivalent from ∂E/∂r = 0 and using ∂L

/∂a = (a −x

)/L

and

∂L

/∂b = (b −y

)/L

leads to two nonlinear equations in a and b:

a =¯x +

=: F(a, b), b =¯y +

=: G(a, b)

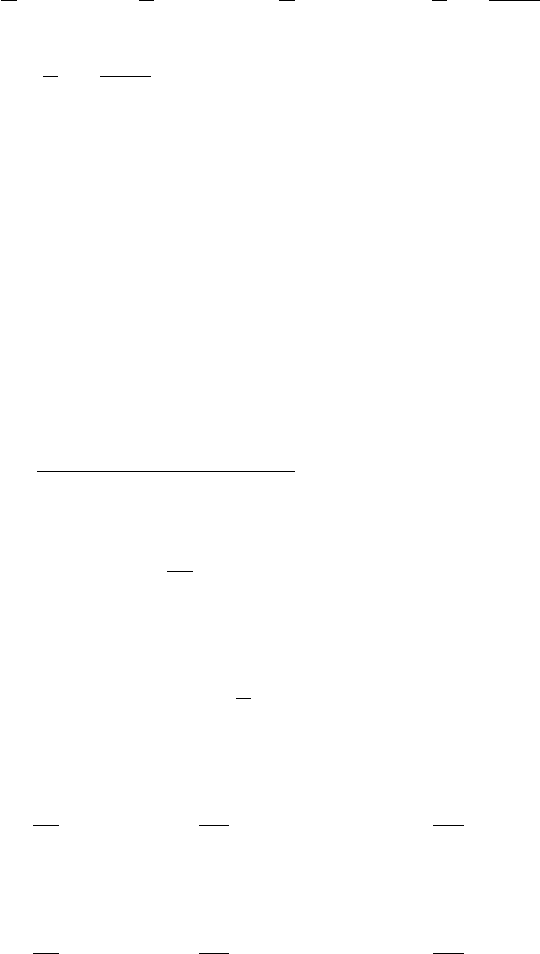
A.7 Least Squares Fitting 887

where

¯x =



i=1

, ¯y =



i=1

L =



i=1



i=1

a −x



i=1

b − y

Fixed point iteration can be applied to solving these equations: a

=¯x, b

=¯y, and

i+1

= F(a

, b

) and b

i+1

= G(a

, b

) for i ≥ 0.

A.7.6 Fitting a Sphere to 3D Points

Given a set of points {(x

, y

, z

)}

i=1

, m ≥ 4, ﬁt them with a sphere (x − a)

+ (y −

+ (z −c)

= r

,where(a, b, c) is the sphere center and r is the sphere radius.

An assumption of this algorithm is that not all the points are coplanar. The energy

function to be minimized is

E(a, b, c, r) =



i=1

− r)

where L

− a)

+ (y

− b)

+ (z

− c). Take the partial derivative with re-

spect to r to obtain

∂E

∂r

=−2



i=1

− r)

Setting equal to zero yields

r =



i=1

Take the partial derivative with respect to a to obtain

∂E

∂a

= 2



i=1

− r)

∂L

∂a

=−2



i=1



− a) + r

∂L

∂a



take the partial derivative with respect to b to obtain

∂E

∂b

= 2



i=1

− r)

∂L

∂b

=−2



i=1



− b) +r

∂L

∂b



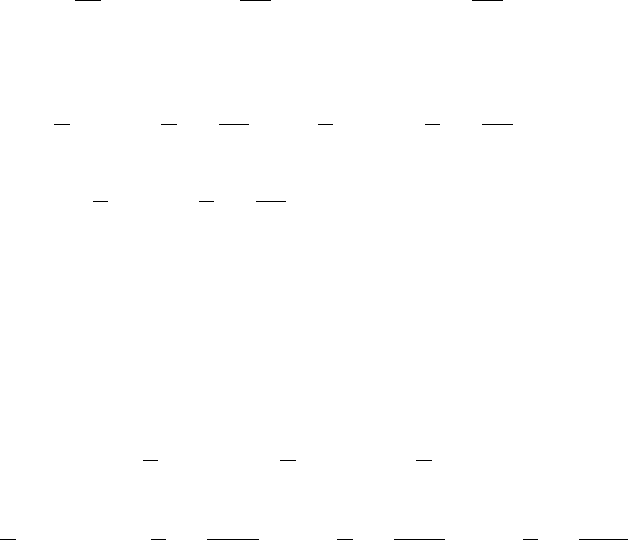
888 Appendix A Numerical Methods

and take the partial derivative with respect to c to obtain

∂E

∂c

= 2



i=1

− r)

∂L

∂c

=−2



i=1



− c) +r

∂L

∂c



Setting these three derivatives equal to zero yields

a =



i=1

+ r



i=1

∂L

∂a

, b =



i=1

+ r



i=1

∂L

∂b

, and

c =



i=1

+ r



i=1

∂L

∂c

Replacing r by its equivalent from ∂E/∂r = 0 and using ∂L

/∂a = (a − x

)/L

∂L

/∂b = (b − y

)/L

, and ∂L

/∂c = (c − z

)/L

leads to three nonlinear equations

in a, b, and c:

a =¯x +

=: F(a, b, c), b =¯y +

=: G(a, b, c), c =¯z +

=: H(a, b, c)

where

¯x =



i=1

, ¯y =



i=1

, ¯z =



i=1

L =



i=1



i=1

a −x



i=1

b − y



i=1

c − z

Fixed point iteration can be applied to solving these equations: a

=¯x, b

=¯y, c

=¯z,

and a

i+1

= F(a

, b

, c

), b

i+1

= G(a

, b

, c

), and c

i+1

= H(a

, b

, c

) for i ≥ 0.

A.7.7 Fitting a Quadratic Curve to 2D Points

Given a set of points {(x

, y

)}

i=0

, a quadratic curve of the form Q(x, y) = c

x + c

y + c

+ c

xy =0 is sought to ﬁt the points. Given values c

that

provide the ﬁt, any scalar multiple provides the same ﬁt. To eliminate this degree of

freedom, require that ˆc = (c

, ..., c

) have unit length. Deﬁne the vector variable

v =(1, x, y, x

, y

, xy). The quadratic equation is restated as Q(v) =ˆc ·v = 0 and is

a linear equation in the space of v. Deﬁne v

= (1, x

, y

, x

, y

, x

) for the ith data

point. While generally Q(v

) is not zero, the idea is to minimize the sum of squares

E(ˆc) =





i=0

ˆc ·v



=ˆc

Mˆc

A.8 Subdivision of Curves 889

where M =



i=0

v

and subject to the constraint ˆc=1. Now the problem is in

the standard format for minimizing a quadratic form, a topic discussed in Section

A.6. The minimum value is the smallest eigenvalue of M, and ˆc is a corresponding

unit-length eigenvector. The minimum itself can be used as a measure of how good

the ﬁt is (0 means the ﬁt is exact).

If there is reason to believe the input points are nearly circular, a minor modiﬁca-

tion can be used in the construction. The circle is of the form Q(x, y) = c

+ c

x +

y +c

) =0. The same construction can be applied where v =(1, x, y, x

) and E(ˆc) =ˆc

Mˆc subject to |ˆc|=1.

A.7.8 Fitting a Quadric Surface to 3D Points

Given a set of points {(x

, y

, z

)}

i=0

, a quadric surface of the form Q(x, y, z) =

+ c

x + c

y + c

z + c

+ c

xy + c

xz + c

yz = 0 is sought to

ﬁt the points. Just like the previous section, ˆc = (c

) is required to be unit length

and v =(1, x, y, z, x

, y

, z

, xy, xz, yz). The quadratic form to minimize is E(ˆc) =

ˆc

Mˆc,whereM =



i=0

v

. The minimum value is the smallest eigenvalue of M,

and ˆc is a corresponding unit-length eigenvector. The minimum itself can be used as

a measure of how good the ﬁt is (0 means the ﬁt is exact).

If there is reason to believe the input points are nearly spherical, a minor mod-

iﬁcation can be used in the construction. The circle is of the form Q(x, y, z) =

x +c

y +c

z + c

) =0. The same construction can be applied

where v =(1, x, y, z, x

+ y

+ z

) and E(ˆc) =ˆc

Mˆc subject to ˆc=1.

A.8 Subdivision of Curves

Sometimes it is desirable to have a polyline approximation to a curve X(t) for t ∈

min

, t

max

]. The methods discussed here apply to any dimension curve. A subdivision

of the curve is a set of points corresponding to an increasing sequence of parameters

}

i=0

⊂[t

min

, t

max

]for a speciﬁed n. Usually the end points of the curve are required

to be in the subdivision, in which case t

min

and t

max

. The subdivision points

are X

= X(t

) for 0 ≤ i ≤ n. A few useful subdivision methods are presented in this

section.

A.8.1 Subdivision by Uniform Sampling

The simplest way to subdivide is to uniformly sample [t

min

, t

max

]. The parameter val-

ues are t

= t

min

+ (t

max

− t

min

)i/n for 0 ≤ i ≤ n. This type of sampling is simple

to implement, but it ignores any intrinsic variation of the curve. Consequently, the

polyline generated by this subdivision is not always a good approximation. The pseu-

docode for the subdivision is

890 Appendix A Numerical Methods

Input: Curve X(t) with t in [tmin, tmax]

n, the number of subdivision points isn+1

Output: subdivision {P[0],...,P[n]}

void Subdivide(int n, Point P[n + 1])

{

for(inti=0;i<=n;i++) {

float t = tmin + (tmax - tmin)*i/n;

P[i] = X(t);

}

A.8.2 Subdivision by Arc Length

This method selects a set of points on the curve that are uniformly spaced along the

curve. The spacing between a pair of points is a distance measurement made along

the curve itself. The distance in this case is called arc length. For example, if the curve

is the semicircle x

+ y

= 1 for y ≥ 0, the distance between the end points (1, 0)

and (−1, 0) is 2 units when measured in the plane. As points on the semicircle, the

distance between the end points is π units, the arc length of the semicircle. The points

= (cos(π i/n), sin(π i/n)) for 0 ≤ i ≤ n are a subdivision of the semicircle. The

distance X

i+1

− X

 measured in the plane varies with i. However, the arc length

between the consecutive pairs of points is π/n, a constant. The points are uniformly

spaced with respect to arc length.

Let L be the total length of the curve. Let t ∈ [t

min

, t

max

] be the curve parameter,

and let s ∈ [0, L] be the arc length parameter. The subdivision is constructed by

ﬁnding those points located at s

= Li/n for 0 ≤ i ≤ n. The technical problem is

to determine t

that corresponds to s

. The process of computing t from a speciﬁed

s is called reparameterization by arc length. This is accomplished by a numerical

inversion of the integral equation relating s to t . Deﬁne Speed(t) =





(t) and

Length(t) =

min







(τ ) dτ. The problem is now to solve Length(t) −s =0 for the

specifed s, a root-ﬁnding task. From the deﬁnition of arc length, the root must be

unique. An application of Newton’s method will sufﬁce (see Section A.5). Evaluation

of Length(t) does require a numerical integration. Various algorithms for numerical

integration are provided in Press et al. (1988). The pseudocode for computing t from

s is

Input: The curve X(t), domain [tmin, tmax], and total length L are available

globally. The Length and Speed calls implicitly use these values. The

value of s must be in [0, L].

Output: The value of t corresponding to s.

float GetParameterFromArcLength(float s)

A.8 Subdivision of Curves 891

{

// Choose an initial guess based on relative location of s in [0,L].

float ratio=s/L;

floatt=(1-ratio) * tmin + ratio * tmax;

for(inti=0;i<imax; i++) {

float diff = Length(t) - s;

if (|diff| < epsilon)

return t;

t -= diff / Speed(t);

}

// Newton’s method failed to converge. Return your best guess.

return t;

}

An application must choose the maximum number of iterations imax and a toler-

ance

epsilon for how close to zero the root is.

The pseudocode for the subdivision is

Input: The curve X(t), domain [tmin, tmax], and total length L are available

globally. The number of subdivision points isn+1.

Output: subdivision {P[0],..., P[n]}

void Subdivide (int n, Point P[n + 1])

{

for(inti=0;i<=n;i++) {

floats=L*i/n;

float t = GetParameterFromArcLength(s);

P[i] = X(t);

}

A.8.3 Subdivision by Midpoint Distance

This scheme produces a nonuniform sampling by recursively bisecting the parameter

space. The bisection is actually performed, and the resulting curve point correspond-

ing to the midpoint parameter is analyzed. If A and B are the end points of the

segment and if C is the computed point in the bisection step, then the distance d

from C to the segment is computed. If d

=B − A, then B is added to the tessel-

lation if d

>εfor an application-speciﬁed maximum relative error of ε>0. The

pseudocode is given below. Rather than maintaining a doubly linked list to handle the

892 Appendix A Numerical Methods

insertion of points on subdivision, the code maintains a singly linked list of ordered

points.

Input: The curve X(t) and domain [tmin, tmax] are available globally.

m, the maximum level of subdivision

epsilon, the maximum relative error

sub {}, an empty list

Output: n >= 1 and subdivision {p[0],..., p[n]}

void Subdivide (int level, float t0, Point X0, float t1, Point X1, List sub)

{

if (level > 0) {

tm=(t0+t1)/2;

Xm = X(tm);

d0 = length of segment <X0, X1>

d1 = distance from Xm to segment <X0, X1>;

if (d1 / d0 > epsilon) {

Subdivide(level - 1, t0, X0, tm, Xm, sub);

Subdivide(level - 1, tm, Xm, t1, X1, sub);

return;

}

sub.Append(X1);

}

Initial call:

List sub = { X(tmin) };

Subdivide(maxlevel, tmin, X(tmin), tmax, X(tmax), sub);

The calculations of d

and d

require expensive square roots. The division d

is also somewhat expensive. An implementation would use squared distances d

and

and make the comparison d

>ε

to reduce the computational costs.

A.8.4 Subdivision by Variation

The subdivision itself can be designed to reﬂect the variation in the curve. A straight-

forward subdivision by uniform sampling does not capture places where the curve

is nearly linear or highly varying. If the goal is to get an extremely accurate distance

measurement, a better method is to recursively subdivide where the subdivision step

is applied based on variation between the curve and the current line segment of in-

A.8 Subdivision of Curves 893

terest. The recursion terminates when all the variations are smaller than a prescribed

tolerance.

The variation metric can be one of many quantities. The one described here is

based on an integral of squared distance between the curve and the line segment. Let

, t

] be the current subinterval under consideration. The curve end points on this

interval are X

= X(t

) for i = 0, 1. The line segment of approximation is

L(t) = X

t − t

− t



− X



The variation is deﬁned by the integral

V([t

, t

]) =

X(t) −L(t)

The difference between the curve and the line segment is a polynomial

X(t) −L(t) =



i=0

where B

= A

− (t

− t

)/(t

− t

), B

= A

− (X

− X

)/(t

− t

), and B

for 2 ≤i ≤n. The squared length is a polynomial of degree 2n:

X(t) −L(t)



i=0



j=0



k=0







m=max{0,k−n}

k−m

· B





so the variation is

V([t

, t

]) =



k=0







m=max{0,k−n}

k−m

· B





k+1

− t

k+1

k + 1

The pseudocode for the subdivision is

Input: The curve X(t) and domain [tmin, tmax] are available globally.

maxlevel, the maximum level of subdivision;

minvariation, the variation tolerance;

sub {}, an empty list;

Output: n >= 1 and subdivision {p[0],..., p[n]};

void Subdivide(int level, float t0, Point X0, float t1, Point X1, List sub)

{

if (level > 0) {