Schneider P., Eberly D.H. Geometric Tools for Computer Graphics

Подождите немного. Документ загружается.

874 Appendix A Numerical Methods

A.5.2 Methods in Many Dimensions

This section discusses the extension of bisection and Newton’s method to many

dimensions.

Bisection

The bisection method for one dimension can be extended to multiple dimensions.

Let (f , g) :[a, b]×[c, d] →R

.Theproblemistoﬁndapoint(x, y) ∈[a, b] ×[c, d]

for which (f (x, y), g(x, y)) =(0, 0). A quadtree decomposition of [a, b] ×[c, d]can

be used for the root search. Starting with the initial rectangle, f and g are evaluated

at the four vertices.

If either f or g has the same sign at the four vertices, the algorithm stops process-

ing that region.

If both f and g have a sign change at the vertices, they are evaluated at the

centerpoint of the region. If the values at the center are close enough to zero, that

point is returned as a root and the search is terminated in that region.

If the center value is not close enough to zero, the region is subdivided into

four subregions by using the original four vertices, the midpoints of the four

edges, and the centerpoint. The algorithm is recursively applied to those four

subregions.

It is possible that when a region is not processed further because f or g has the

same sign at all four vertices, the region really does contain a root. The issue is the

same as for one dimension—the initial rectangle needs to be partitioned to locate

subrectangles on which a root is bound. The bisection method can be applied to each

subrectangle that contains at least one root.

For three dimensions, an octree decomposition is applied in a similar way. For n

dimensions, a 2

-tree decomposition is used.

Newton’s Method

Given differentiable F : R

→ R

, the equation F(x) =



0 can be solved by the ex-

tension of Newton’s method in one dimension. The iteration scheme that directly

generalizes the method is to select an initial guess (x

, F(x

)) and generate the next

iterate by

x

=x

− (DF(x

))

−1

F(x

)

The quantity DF(x) is the matrix of partial derivatives of F , called the Jaco-

bian matrix, and has entries ∂F

/∂x

,whereF

is the ith component of F and x

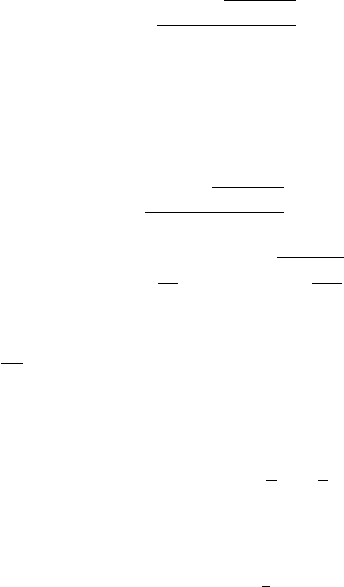
A.5 Root Finding 875

is the jth component of x. Each iterate requires a matrix inversion. While the obvi-

ous extension, it is not always the best to use. There are variations on the method

that work much better in practice, some of those using what are called splitting

methods that avoid having to invert a matrix and usually have better convergence

behavior.

A.5.3 Stable Solution to Quadratic Equations

The general form of the quadratic is

+ bx +c = 0

and the solution is

λ =

−b ±

√

− 4ac

However, simply solving this problem in the “obvious” way can result in numer-

ical problems when implemented on a computer. We can see this if we rearrange the

standard solution (Casselman 2001):

, x

−b ±

√

− 4ac







−1 ±



1 −

4ac



If the quantity

4ac

is very small, then one of these involves the subtraction of two

nearly equal-sized positive numbers—this can result in a large rounding error.

However, if we rewrite the quadratic equation by factoring out a

+ bx +c = a(x

x +

)

= a(x − x

)(x −x

)

then we see that the product of the two roots is

. We can avoid the problem noted

above by doing the operations in this order:

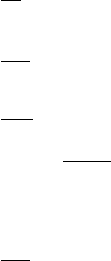
876 Appendix A Numerical Methods

A ←

B ←

4ac

←

C ←−1 −

√

1 − B

← AC

←

A.6 Minimization

The generic problem is to ﬁnd a global minimum for a function f : D ⊂R

→R.The

function is constrained to be at least continuous, and D is assumed to be a compact

set. If the function is continuously differentiable, this fact can help in locating a

minimum, but there are methods that do not require derivatives in ﬁnding one.

A.6.1 Methods in One Dimension

Consider f :[t

min

, t

max

] → R.Iff is differentiable, then the global minimum must

occur either at a point where f



= 0 or at one of the end points. This standard

approach is what is used in computing distance between a point and a line segment

(see Section 6.1.3 on distance methods). The squared-distance function is quadratic

and is deﬁned on a compact interval. The minimum of that function occurs at an

interior point of the interval (closest point is interior to line segment) or at an end

point. Solving the problem f



(t) = 0 may be complicated in itself. This is a root-

ﬁnding problem that is described in Section A.5.

Brent’s Method

Continuous functions that are not necessarily differentiable must attain a minimum

on a compact interval. A method to ﬁnd the minimum that does not require deriva-

tives or does not require determining where the derivative is zero when the function

is differentiable is very desirable. One such method is called Brent’s method and uses

inverse parabolic interpolation in an iterative fashion.

A.6 Minimization 877

Theideaistobracket the minimum by three points (t

, f(t

)), (t

, f(t

)), and

, f(t

)) for t

min

≤t

max

,wheref(t

)<f(t

) and f(t

)<f(t

). This

means the function must decrease for some values of t ∈[t

, t

]and must increase for

some values of t ∈ [t

, t

]. This guarantees that f has a local minimum somewhere

in [t

, t

]. Brent’s method attempts to narrow in on the local minimum, much like the

bisection method narrows in on the root of a function (see Section A.5).

The following is a variation of what is described for Brent’s method in Press

et al. (1988). The three bracketing points are ﬁt with a parabola, p(t).Thevertex

of the parabola is guaranteed to lie within (t

, t

).Letf

= f(t

), f

= f(t

), and

= f(t

). The vertex of the parabola occurs at t

∈ (t

, t

) and can be shown to be

= t

−

− t

)

− f

) − (t

− t

)

− f

)

− t

)(f

− f

) − (t

− t

)(f

− f

)

The function is evaluated there, f

= f(t

).Ift

, then the new bracket is

, f

), (t

, f

), and (t

, f

).Ift

, then the new bracket is (t

, f

), (t

, f

), and

, f

).Ift

= t

, the bracket cannot be updated in a simple way. Moreover, it is not

sufﬁcient to terminate the iteration here, as it is simple to construct an example where

the three samples form an isosceles triangle whose vertex on the axis of symmetry is

the parabola vertex, but the global minimum is far away from that vertex. One simple

heuristic is to use the midpoint of one of the half-intervals, say, t

= (t

+ t

)/2,

evaluate f

= f(t

), and compare to f

.Iff

, then the new bracket is (t

, f

), and (t

, f

).Iff

, then the new bracket is (t

, f

), (t

, f

), and (t

, f

If f

, the other half-interval can be bisected and the same tests repeated. If that

also produces the pathological equality case, try a random sample from [t

, t

]. Once

the new bracket is known, the method can be repeated until some stopping criterion

is met.

Brent’s method can be modiﬁed to support derivative information. A description

of that also occurs in Press et al. (1988).

A.6.2 Methods in Many Dimensions

Consider f : D ⊂ R

→ R,whereD is a compact set. Typically in graphics applica-

tions, D is a polyhedron or even a Cartesian product of intervals. If f is differentiable,

then the global minimum must occur either at a point where



∇f =



0oronthe

boundary of D. In the latter case if D is a polyhedron, then the restriction of f to

each face of D produces the same type of minimization problem, but in one less di-

mension. For example, this happens for many of the distance methods described in

Chapter 10 on geometrical methods. Solving the problem



∇f =



0 is a root-ﬁnding

problem and itself may be a difﬁcult problem to solve.

878 Appendix A Numerical Methods

Steepest Descent Search

This is a simple approach to searching for a minimum of a differentiable function.

From calculus it is known that the direction in which f has its greatest rate of

decrease is −



∇f . Given an initial guess x for the minimum point, the function

φ(t) = f(x − t



∇f(x)) is minimized using a one-dimensional algorithm. If t



is the

parameter at which the minimum occurs, then x ←x − t





∇f(x) and the algorithm

is repeated until a stopping condition is met. The condition is typically a measure of

how different the last starting position is from the newly computed position.

The problem with this method is that it can be very slow. The pathological case

is the minimization of a paraboloid f(x, y) = (x/a)

+ y

,wherea is a very large

number. The level sets are ellipses that are very elongated in the x-direction. For

points not on the x-axis, the negative of the gradient vector tends to be nearly parallel

to the y-axis. The search path will zigzag back and forth across the x-axis, taking its

time getting to the origin where the global minimum occurs. A better approach is not

to use the gradient vector but to use something called the conjugate direction. For the

paraboloid, no matter where the initial guess is, only two iterations using conjugate

directions will always end up at the origin. These directions in a sense encode shape

information about the level curves of the function.

Conjugate Gradient Search

This method attempts to choose a better set of directions than steepest descent for a

minimization search. The main ideas are discussed in Press et al. (1988), but a brief

summary is given here. Two sequences of directions are built, a sequence of gradi-

ent directions g

and a sequence of conjugate directions



. The one-dimensional

minimizations are along lines corresponding to the conjugate directions. The follow-

ing pseudocode uses the Polak and Ribiere formulation as mentioned in Press et al.

(1988). The function to be minimized is E(x). The function

MinimizeOn minimizes

the function along the line using a one-dimensional minimizer. It returns the location

x of the minimum and the function value fval at that minimum.

x = initial guess;

g = -gradient(E)(x);

h=g;

while (not done) {

line.origin = x;

line.direction = h;

MinimizeOn(line, x, fval);

if (stopping condition met)

return <x, fval>;

gNext = -gradient(E)(x);

A.6 Minimization 879

c = Dot(gNext - g, gNext) / Dot(g, g);

g = gNext;

h=g+c*h;

}

The stopping condition can be based on consecutive values of fval and/or on

consecutive values of

x. The condition in Press et al. (1988) is based on consecutive

function values, f

and f

, and a small tolerance value τ>0,

2|f

− f

|≤τ(|f

|+|f

|+.)

for a small value .>0 that supports the case when the function minimum is zero.

Powell’s Direction Set Method

If f is continuous but not differentiable, then it attains a minimum on D.The

search for the minimum simply cannot use derivative information. A method to ﬁnd

a minimum that does not require derivatives is Powell’s direction set method. This

method solves minimization problems along linear paths in the domain. The current

candidate for the point at which the minimum occurs is updated to the minimum

point on the current line under consideration. The next line is chosen to contain the

current point and has a direction selected from a maintained set of direction vectors.

Once all the directions have been processed, a new set of directions is computed.

This is typically all but one of the previous set, but with the ﬁrst direction removed

and the new direction set to the current position minus the old position before the

line minimizations were processed. The minimizations along the lines use something

such as Brent’s method since f restricted to the line is a one-dimensional function.

The fact that D is compact guarantees that the intersection of the line with D is a

compact set. Moreover, if D is convex (which in most applications it is), then the

intersection is a connected interval so that Brent’s method can be applied to that

interval (rather than applying it to each connected component of the intersection

of the line with D). The pseudocode for Powell’s method is

// F(x) is the function to be minimized

n = dimension of domain;

directionSet = {d[0],..., d[n - 1]}; // usually the standard axis directions

x = xInitial = initial guess for minimum point;

while (not done) {

for (each direction d) {

line.origin = x;

line.direction = d;

MinimizeOn(line, x, fval);

}

880 Appendix A Numerical Methods

conjugateDirection=x-xInitial;

if (Length(conjugateDirection) is small)

return <x, fval>; // minimum found

for(i=0;i<=n-2;i++)

d[i] = d[i + 1];

d[n - 1] = conjugateDirection;

}

The function MinimizeOn is the same one mentioned in the previous subsection

on the conjugate gradient search.

A.6.3 Minimizing a Quadratic Form

Let A be an n × n symmetric matrix. The function Q : R

→ R deﬁned by Q( ˆv) =

ˆv

A ˆv for ˆv=1 is called a quadratic form. Since Q is deﬁned on the unit sphere

in R

, a compact set, and since Q is continuous, it must have a maximum and a

minimum on this set.

Let ˆv =



i=1

,whereA ˆv

=λ

ˆv

, λ

≤···≤λ

, and



i=1

=1. That is, the

are the eigenvalues of A, and the ˆv

are the corresponding eigenvectors. Expanding

the quadratic yields

Q( ˆv) =





i=1

ˆv









j=1

ˆv







i=1



j=1

ˆv

A ˆv



k=1

The rightmost summation is a convex combination of the eigenvalues of A,so

its minimum is λ

and occurs when c

= 1 and all other c

= 0. Consequently,

min Q( ˆv) = λ

= Q( ˆv

A.6.4 Minimizing a Restricted Quadratic Form

In some applications it is desirable to ﬁnd the minimum of a quadratic form deﬁned

on the unit hypersphere S

n−1

, but restricted to the intersection of this hypersphere

with a hyperplane ˆn · X = 0 for some special normal vector ˆn.LetA be an n × n

symmetric matrix. Let ˆn ∈ R

be a unit-length vector. Let ˆn

⊥

denote the orthogonal

complement of ˆn. Deﬁne Q : {ˆn}

⊥

→ R by Q( ˆv) =ˆv

A ˆv,whereˆv=1. Now Q is

deﬁned on the unit sphere in the (n − 1)-dimensional space ˆn

⊥

, so it must have a

maximum and a minimum.

Let ˆv

through ˆv

n−1

be an orthonormal basis for ˆn

⊥

.Let ˆv =



n−1

i=1

ˆv

,where



i=1

= 1. Let A ˆv



n−1

j=1

ˆv

+ α

ˆn,whereα

=ˆv

A ˆv

for 1 ≤ i ≤ n − 1

A.6 Minimization 881

and 1 ≤j ≤n −1, and where α

=ˆn

A ˆv

for 1 ≤i ≤ n −1. Expanding the quadratic

form yields

Q( ˆv) =



n−1



i=1

ˆv







n−1



j=1

ˆv





n−1



i=1

n−1



j=1

=c

Ac =: P(c)

where quadratic form P : R

n−1

→ R satisﬁes the conditions for the minimization in

the last section. Thus, min Q( ˆv) = min P(c), which occurs for c and λ such that

Ac = λc and λ is the minimum eigenvalue of

A. The following calculations lead to a

matrix formulation for determining the minimum value:

n−1



j=1

= λc

n−1



j=1

ˆv

= λc

ˆv

n−1



i=1

n−1



j=1

ˆv

= λ

n−1



i=1

ˆv



j=1



n−1



i=1

ˆv



= λ ˆv

n−1



j=1



A ˆv

− α

ˆn



= λ ˆv





n−1



j=1

ˆv





−





n−1



j=1





ˆn = λ ˆv

A ˆv −



ˆn

A ˆv



ˆn = λ ˆv

(I −ˆn ˆn

)A ˆv =λ ˆv

Therefore, min Q( ˆv) = λ

= Q( ˆv

),whereλ

is the minimum positive eigenvalue

corresponding to the eigenvector ˆv

of (I −ˆn ˆn

)A. Note that n −1 of the eigenvectors

are in ˆn

⊥

. The remaining eigenvector is ˆv

= A

adj

ˆn,whereAA

adj

= (det A)I and

= 0.

882 Appendix A Numerical Methods

A.7 Least Squares Fitting

Least squares ﬁtting is the process of selecting a parameterized equation that repre-

sents a discrete set of points in a continuous manner. The parameters are estimated by

minimizing a nonnegative function of the parameters. This section discusses ﬁtting

by lines, planes, circles, spheres, quadratic curves, and quadric surfaces.

A.7.1 Linear Fitting of Points (x, f (x))

This is the usual introduction to least squares ﬁt by a line when the data represents

measurements where the y-component is assumed to be functionally dependent on

the x-component. Given a set of samples {(x

, y

)}

i=1

, determine a and b so that

the line y = ax + b best ﬁts the samples in the sense that the sum of the squared

errors between the y

and the line values ax

+ b is minimized. Note that the error is

measured only in the y-direction.

Deﬁne E(a, b) =



i=1

[(ax

+ b) − y

]

. This function is nonnegative, and its

graph is a paraboloid whose vertex occurs when the gradient satisﬁes



∇E = (0, 0).

This leads to a system of two linear equations in a and b that can be easily solved.

Precisely,

(0, 0) =



∇E =2



i=1

[(ax

+ b) −y

](x

,1)

and so





i=1



i=1



i=1



i=1









i=1



i=1



The solution provides the least squares solution y =ax +b.

A.7.2 Linear Fitting of Points Using Orthogonal

Regression

It is also possible to ﬁt a line using least squares where the errors are measured

orthogonally to the proposed line rather than measured vertically. The following

argument holds for sample points and lines in n dimensions. Let the line be L(t) =

d + A,where

d is unit length. Deﬁne X

to be the sample points; then

= A + d

d + p

⊥

A.7 Least Squares Fitting 883

where d

d · (X

− A) and

⊥

is some unit-length vector perpendicular to

d with

appropriate coefﬁcient p

. Deﬁne y

= X

− A. The vector from X

to its projection

onto the line is

y

− d

d = p

⊥

The squared length of this vector is p

=(y

−d

. The energy function for the least

squares minimization is E(A,

d) =



i=1

. Two alternate forms for this function

are

E(A,

d) =



i=1



y



I −



y



and

E(A,

d) =





i=1

(y

·y

)I −y

y



d =

M(A)

Using the ﬁrst form of E in the previous equation, take the derivative with respect to

A to get

∂E

∂A

=−2



I −





i=1

y

This partial derivative is zero whenever



i=1

y

= 0, in which case A = (1/m)



i=1

, the average of the sample points.

Given A, the matrix M(A) is determined in the second form of the energy func-

tion. The quantity

M(A)

d is a quadratic form whose minimum is the smallest

eigenvalue of M(A). This can be found by standard eigensystem solvers. A corre-

sponding unit-length eigenvector

d completes our construction of the least squares

line.

For n = 2, if A = (a, b), then matrix M(A) is given by

M(A) =





i=1

− a)



i=1

− b)







−





i=1

− a)



i=1

− a)(y

− b)



i=1

− a)(y

− b)



i=1

− b)

