Schneider P., Eberly D.H. Geometric Tools for Computer Graphics
Подождите немного. Документ загружается.


914 Appendix A Numerical Methods
which yields a pair of equations
2x =λ(34x + 12y)
2y =λ(12x +16y)
There are two cases to consider.
Case 1 Assume that 34x +12y = 0 and 12x + 16y = 0. We need to solve the equations for
λ and equate them:
2x
34x +12y
=
2y
12x +16y
2x(12x +16y) = 2y(34x + 12y)
12x
2
+ 16xy = 34xy +12y
2
2x
2
− 3xy − 2y
2
= 0
This yields the system
17x
2
+ 12xy + 8y
2
= 100
2x
2
− 3xy − 2y
2
= 0
which has solutions (2, 1), (2, −4), (−2, −1), (−2, 4). We then plug these into the
equation:
f(2, 1) = 5
f(−2, −1) = 5
f(2, −4) = 20
f(−2, 4) = 20
Case 2 Either 34x +12y =0or12x +16y =0, but in either of these cases, x =y =0, which
doesn’t satisfy the ellipse equation.
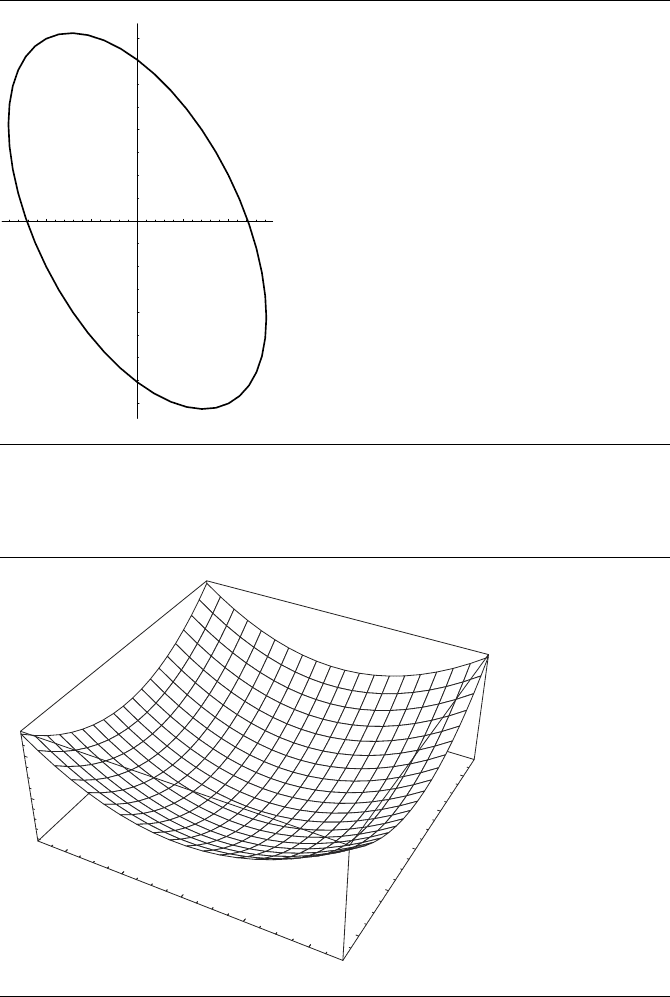
The geometric intuition can be assisted by looking at the plots of the functions
involved. Figure A.18 shows the ellipse 17x
2
+8y
2
+12xy =100. The objective func-
tion x
2
+ y
2
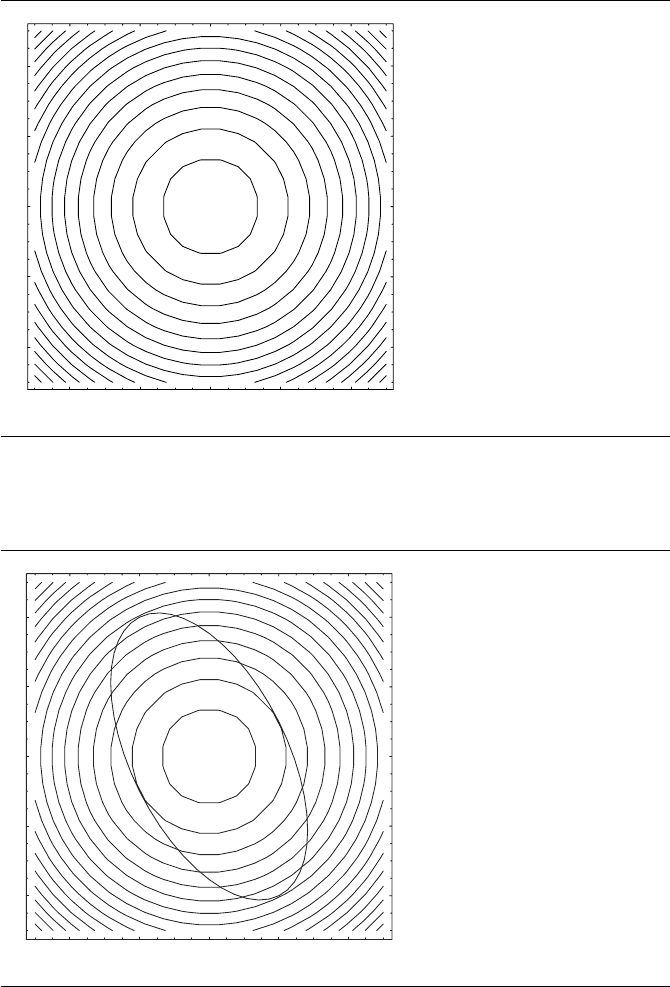
is shown in Figure A.19, and various level curves for it in Figure A.20.
If we plot both the ellipse and the level curves together, then we can see the point
of mutual tangency at (2, 1) and (−2, −1) (the minimizing solutions), and at (2, −4)
and (−2, 4) (the maximizing solutions)—see Figure A.21.
A.9 Topics from Calculus 915
–2 –1 1 2
–4
–2
2
4
Figure A.18 Plot of the ellipse 17x
2
+ 8y
2
+ 12xy = 100.
–2
0
2
4
–4
–2
0
2
4
0
20
40
–4
Figure A.19 Plot of the function x
2
+ y
2
.
916 Appendix A Numerical Methods
–4 –2 0 2 4
–4
–2
0
2
4
Figure A.20 Level curves for x
2
+ y
2
.
–4 –2 0 2 4
–4
–2
0
2
4
Figure A.21
The constraint curve and the ellipse are tangent at the minima.
A.9 Topics from Calculus 917
Three-Variable Extrema Problems
Lagrange multipliers can also be applied to the problem of finding the extrema of
functions in three variables, subject to one or two constraints.
Single Constraint
In the case of a single constraint, we wish to maximize or minimize f(x, y, z) subject
to a constraint g(x, y, z) = 0. The graph of a three-variable function of the form
g(x, y, z) = 0 is a surface S in 3-space. The geometric intuition here is that we are
looking for the maximum or minimum of f(x, y, z) as (x, y, z) varies over the
surface S. The function f(x, y, z) has a constrained relative maximum at some point
(x
0
, y
0
, z
0
) if that point is the center of a sphere, with
f(x
0
, y
0
, z
0
) ≥ f(x, y, z)
for all points on S that are within this sphere. If the maximum value of f is f(x
0
, y
0
,
z
0
) = c, then the level surface f(x, y, z) = c is tangent to the level surface g, and so
their gradient vectors at that point are parallel:
∇f(x
0
, y
0
, z
0
) = λ∇g(x
0
, y
0
, z
0
)
To solve a problem of this type, we must do the following:
1. Find all values of x, y, z that satisfy
∇f(x
0
, y
0
, z
0
) = λ∇g(x
0
, y
0
, z
0
)
and
g(x
0
, y
0
, z
0
) = k
This is done by solving, as before, a set of simultaneous equations.
2. Evaluate the function f at all the points from step 1 to determine which is (are)
the maximum value and which is (are) the minimum value.
An example should help illustrate this.
Find the point on the sphere x
2
+y
2
+z
2
=36 that is closest to the point (1, 2, 2).
That is, we wish to find the point (x
0
, y
0
, z
0
) that minimizes the distance (squared)
function f(x, y, z) = (x − 1)
2
+ (y − 2)
2
+ (z − 2)
2
, subject to the constraint that
the point lies on the sphere g(x, y, z) = x
2
+ y
2
+ z
2
= 36. Equating ∇f(x, y, z) =
λ∇g(x, y, z) for this problem we have
2(x −1)i + 2(y − 2)j + 2(z − 2)k =λ(2xi + 2yj +2zk)
918 Appendix A Numerical Methods
which gives us this system:
2(x −1) = 2xλ
2(y −2) = 2yλ
2(z − 2) = 2zλ
(A.12)
As the sphere is centered at the origin, and none of the components of the point are 0,
the nearest point cannot have any components that are 0, and so there are no special
cases to consider as in the previous example. We can then rewrite System A.12 as
x −1
x
= λ
y −2
y
= λ
z − 2
z
= λ
(A.13)
The first two equations give us
x −1
x
=
y −2
y
xy − y = xy −2x
y =2x
(A.14)
while the first and third give us
x −1
x
=
z − 2
z
xz − z = xz − 2x
z = 2x
(A.15)
Substituting these results back into the constraint equation (that is, the sphere equa-
tion), we get
9x
2
= 36
or
x =±2
If we substitute these back into Equations A.14 and A.15, we get the two points
(2, 4, 4) and (−2, −4, −4). Plugging these values back into f ,wehavef(2, 4, 4) = 9
A.9 Topics from Calculus 919
–5
–2.5
0
2.5
5
x
–5
–2.5
0
2.5
5
y
–5
–2.5
0
2.5
5
z
Figure A.22 The closest and farthest point to (1, 2, 2) on the sphere x
2
+ y
2
+ z
2
= 36.
and f(−2, −4, −4) = 81, and so we can conclude that the closest point is (2, 4, 4);
see Figure A.22.
An alternative way of looking at this is that we’re solving a system of four equa-
tions in four variables
∂f
∂x
(x
0
, y
0
, z
0
) = λ
∂g
∂x
(x
0
, y
0
, z
0
)
∂f
∂y
(x
0
, y
0
, z
0
) = λ
∂g
∂y
(x
0
, y
0
, z
0
)
∂f
∂z
(x
0
, y
0
, z
0
) = λ
∂g
∂z
(x
0
, y
0
, z
0
)
g(x
0
, y
0
, z
0
) = 0
or
2
(
−1 + x
)
= 2 xλ
2
(
−2 +y
)
= 2 yλ
2
(
−2 +z
)
= 2 zλ
x
2
+ y
2
+ z
2
− 36 =0
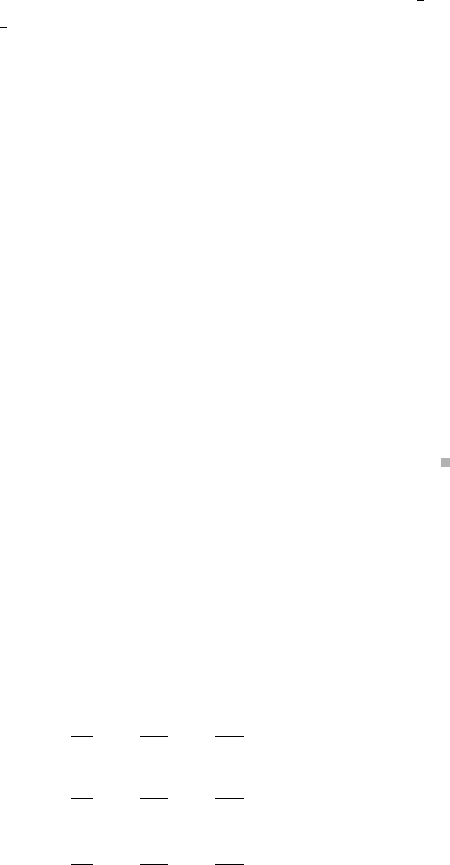
920 Appendix A Numerical Methods
which can be solved using standard techniques. This gives us the (same) results
directly, including the actual values of the Lagrange multipliers: {{λ →
1
2
, x → 2,
y →4, z → 4}, {λ →
3
2
, x →−2, y →−4, z →−4}}.
Two Constraints
If we have a function of three variables, we can have two constraints.
Theorem A.10 Constrained Extremum Principle—Three-Variable Form with Two Constraints: If there
is an extremum for f(x, y, z) on the constraint curve determined by the intersection
of the implicit surfaces defined by g
1
(x, y, z) = 0 and g
2
(x, y, z) = 0, then it occurs
at a point (x
0
, y
0
, z
0
) satisfying all of
∇f(x
0
, y
0
, z
0
) = λ
1
∇g
1
(x
0
, y
0
, z
0
)
∇f(x
0
, y
0
, z
0
) = λ
2
∇g
2
(x
0
, y
0
, z
0
)
g
1
(x
0
, y
0
, z
0
) = 0
g
2
(x
0
, y
0
, z
0
) = 0
That is, the gradient of f must be parallel to the gradients of both g
1
and g
2
.
Again, an example can help illuminate this: find the extreme values of f(x, y, z) =
x +2y +3z =0, subject to the constraints g
1
(x, y, z) =x −y +z =1 and g
2
(x, y, z)
= x
2
+ y
2
= 1. Geometrically speaking, the two constraints represent a plane and a
cylinder, respectively; these intersect in an ellipse. The function f is another plane,
and so we’re looking to find the extrema of this plane on the ellipse. Figure A.23 shows
constraint functions g
1
and g
2
, which intersect in an ellipse.
Theorem A.10 states that the extrema can be found by solving a system of equa-
tions. For this example, our equations can be stated as
∂f
∂x
= λ
1
∂g
1
∂x
+ λ
2
∂g
2
∂x
∂f
∂y
= λ
1
∂g
1
∂y
+ λ
2
∂g
2
∂y
∂f
∂z
= λ
1
∂g
1
∂z
+ λ
2
∂g
2
∂z
g
1
= x − y + z − 1
g
2
= x
2
+ y
2
− 1
which is
A.9 Topics from Calculus 921
–2
–1
0
1
2
x
–2
–1
0
1
2
y
–2
0
2
z
–2
–1
0
1
2
x
–2
–1
0
1
2
y
–2
0
2
z
Figure A.23 Constraint equations g
1
(x, y, z) = x −y +z = 1 and g
2
(x, y, z) = x
2
+ y
2
= 1.
1 = 2 xλ
1
+ 2 xλ
2
2 =2 yλ
1
+ 2 yλ
2
3 = 2 zλ
1
x
2
+ y
2
+ z
2
− 36 =0
x
2
+ y
2
− 1 = 0
and which can be solved using standard techniques to yield
λ
1
→ 3, λ
2
→
−
√
29
2
, x →
2
√
29
, y →
−5
√
29
, z →
29 −7
√
29
29
,
λ
1
→ 3, λ
2
→
√
29
2
, x →
−2
√
29
, y →
5
√
29
, z →
29 +7
√
29
29
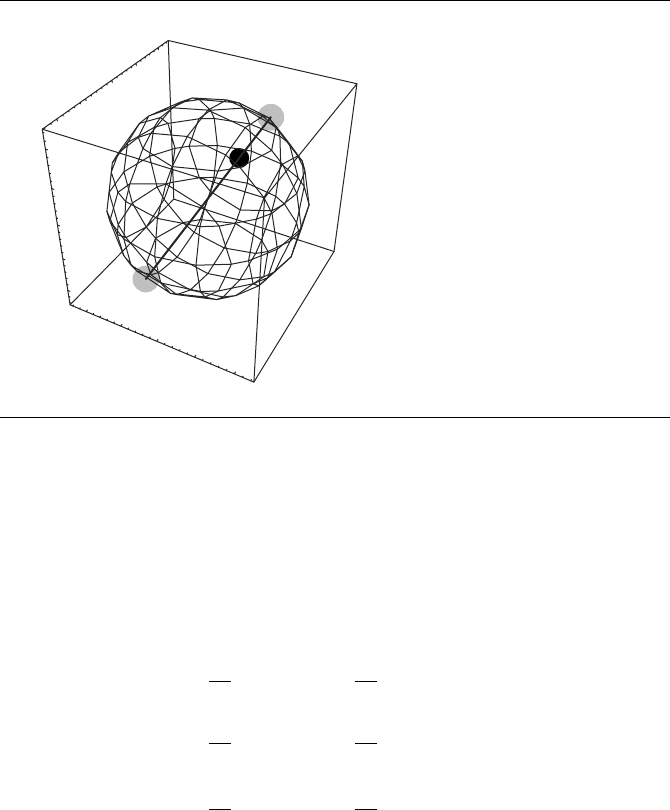
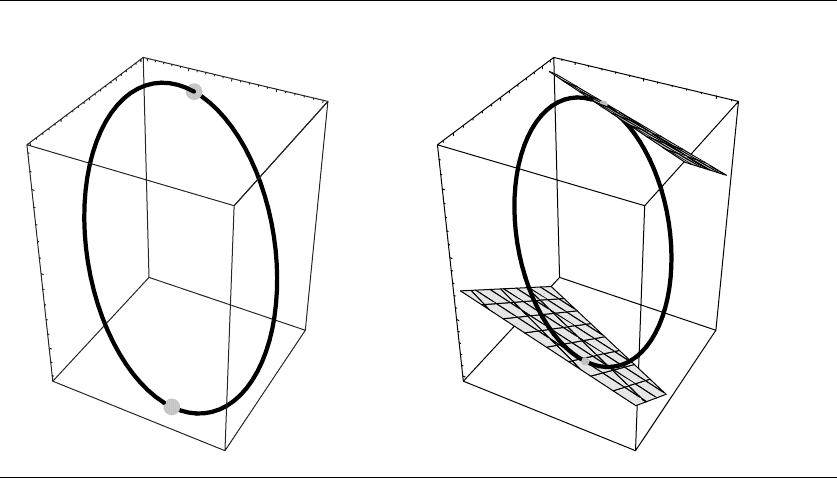
These points—the minimum and maximum—are shown on the constraint curve
determined by the intersection of the implicit surfaces defined by g
1
= 0 and g
2
= 0
in Figure A.24.
922 Appendix A Numerical Methods
–1
–0.5
0
0.5
1
x
–1
–0.5
0
0.5
1
y
0
1
2
z
–1
0
1
x
–1
0
1
y
z
–1
0
1
2
Figure A.24 Extrema of f shown as points on the constraint curve determined by the intersection of
implicit surfaces defined by g
1
= 0 and g
2
= 0, and the level sets of f at those extrema.
Appendix
BTrigonometry
B.1 Introduction
This appendix serves as a review of some fundamental trigonometry that you may
find useful, as well as a handy reference for commonly used definitions and relation-
ships of trigonometric functions.
B.1.1 Terminology
Trigonometry is generally concerned with angles between lines (or more properly,
half-lines or rays) in the plane. By convention, the ray from which an angle is mea-
suredistermedtheinitial side, and the ray to which the angle θ is measured is termed
the terminal side. Angles are considered positive if measured in a counterclockwise
direction and negative if measured in a clockwise direction.
The end point of the two rays in question is termed the vertex. An angle whose
vertex is at the origin and whose initial side lies along the positive x-axis is in standard
position (see Figure B.1).
B.1.2 Angles
The angle θ between two rays is measured in either degrees or radians. Degrees
are more common in informal or popular usage, and radians are more common in
technical usage. If we consider a ray that is swept starting from the initial side, and
continuing until the terminal side again coincides with the initial side, the end point
923
