Schneider P., Eberly D.H. Geometric Tools for Computer Graphics

Подождите немного. Документ загружается.

894 Appendix A Numerical Methods

var = Variation(t0, X0, t1, X1);

if (var > minvariation) {

tm=(t0+t1)/2;

xmid = X(tm);

Subdivide(level - 1, t0, X0, tm, Xm, sub);

Subdivide(level - 1, tm, Xm, t1, X1, sub);

return;

}

sub.Append(X1);

}

Initial call:

List sub = { X(tmin) };

Subdivide(maxlevel, tmin, X(tmin), tmax, X(tmax), sub);

The maxlevel parameter avoids deep recursive calls when a small minvariation is

speciﬁed. However, if

level reaches zero, the variation for the current interval is not

necessarily within the speciﬁed tolerance. Since the variation does not provide error

bounds for the distance calculation, this is not a problem.

A.9 Topics from Calculus

This section reviews several topics from calculus that can be useful in solving a

number of problems discussed in this book, particularly distance and intersection.

A.9.1 Level Sets

Political maps show boundaries of states and countries, and some amount of geo-

graphical features (rivers, oceans, etc.), but these are often shown indicatively. Topo-

graphic maps, on the other hand, are useful because they explicitly show the elevation

of the land. This is done by the use of contours—curves representing the cross section

of the land at a particular altitude. By observing the altitude markings associated with

particular contours, as well as their topology, the map user can easily distinguish in-

clines, peaks, and valleys. Further, the steepness of a slope can easily be discerned,

by the relative distance between adjacent contours—the closer together they are, the

steeper the slope.

A contour map can be considered to be a way of visualizing a function of two

variables f(x, y) =z,wherex and y are the latitude and longitude and z is the height

(altitude). If we intersect the function f with a horizontal plane

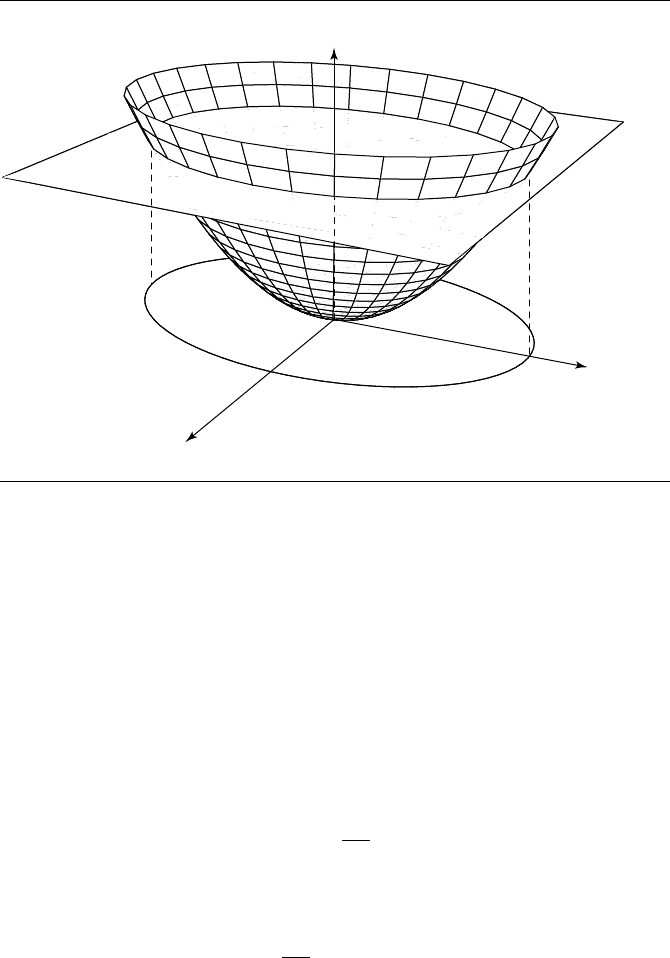
A.9 Topics from Calculus 895

Figure A.2 Intersection of a function f(x, y) = z and plane z = 0.8 yields a level curve, shown

projected on the xy-plane.

z = h

and project the resulting curve onto the xy-plane, then we get what is referred to as

a level curve (see Figure A.2). This level curve has the equation

f(x, y) = a

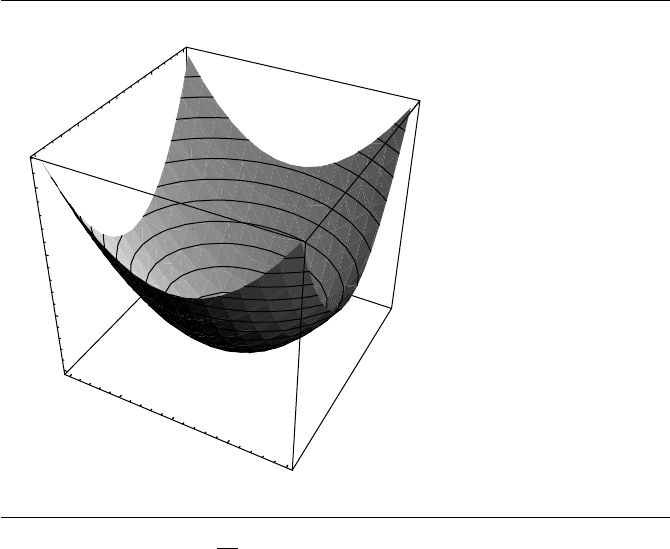
If we have the paraboloid

f(x, y) =

+ y

(see Figure A.3), then the level curves have equations of the form

+ y

= h

For h>0, these are ellipses; for h =0, it is a point; and for h<0, there are no curves.

A number of the projected level curves are shown in Figure A.4.

896 Appendix A Numerical Methods

–1

–0.5

0.5

–1

–0.5

0.5

1.5

Figure A.3 Level curves for f(x, y) =

+ y

Level curves of a function f(x, y) and the gradient of the function ∇f(x, y) have

an important geometric relationship. Suppose we have any point (in f ’s domain, of

course) x

, y

and that f(x

, y

) = c for some constant c. We know that f(x, y) = c

deﬁnes some level curve for f , and that f(x

, y

) is a point on that curve. The

maximum rate of increase for f at (x

, y

) is in the direction of ∇f(x

, y

) and

the minimum in the direction of −∇f(x

, y

). Intuitively, it seems, then, that the

gradient must be perpendicular to the level curve at f(x

, y

), and this indeed turns

out to be the case. An outline of the proof follows (Anton 1980).

Assume we have a level curve

f(x, y) = c (A.9)

through (x

, y

). We can represent this curve parametrically, as

x =x(t)

y =y(t)

which has a nonzero tangent vector at (x

, y

)

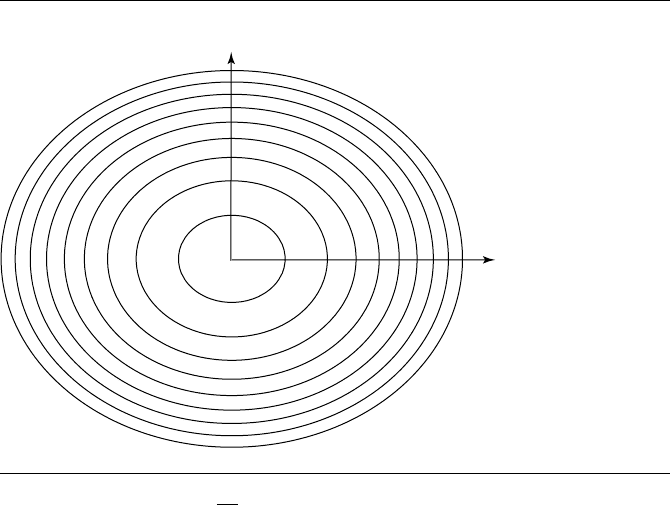
A.9 Topics from Calculus 897

Figure A.4 Level curves for f(x, y) =

+ y

, projected onto the xy-plane.



)i + y



j = 0

where t

is the value of the parameter at the point (x

, y

If we differentiate Equation A.9 with respect to t and apply the chain rule, we get

(x(t), y(t))x



(t) + f

(x(t), y(t))y



(t) = 0

Using the facts that x(t

) = x

and y(t

) = y

, and substituting t = t

,weget

, y



) + f

, y



) = 0

which can be rewritten as

∇f(x

, y

) · (x



)i + y



)j) = 0

That is, ∇f(x

, y

) is perpendicular to the tangent vector of the level curve at (x

, y

898 Appendix A Numerical Methods

No minimum No maximum

Figure A.5 Two functions lacking either a minimum or maximum value.

A.9.2 Minima and Maxima of Functions

This section addresses the problem of ﬁnding the minimum and maximum values of

a function, in both one and two variables. Such problems arise often in the context

of optimization problems—informally, situations in which we want to ﬁnd the “best”

(or perhaps “worst”) solution.

Functions of One Variable

Given a function f , we might wish to know various facts about minimum or maxi-

mum values (the extrema), such as

Does f(x)have a minimum (maximum) value?

If f(x)has a minimum (maximum), what is it, and where does it occur?

Does f(x)have a minimum (maximum) within an interval [a, b]or [a, b)?

Figure A.5 shows two functions, one of which has no minimum value over its domain,

and the other no maximum value.

We begin with some relevant deﬁnitions

Deﬁnition

A.1

A number M is called an absolute maximum value for a function f with domain D if

i. f(x)≤ M, ∀x ∈D.

ii. ∃x ∈ D|f(x)= M.

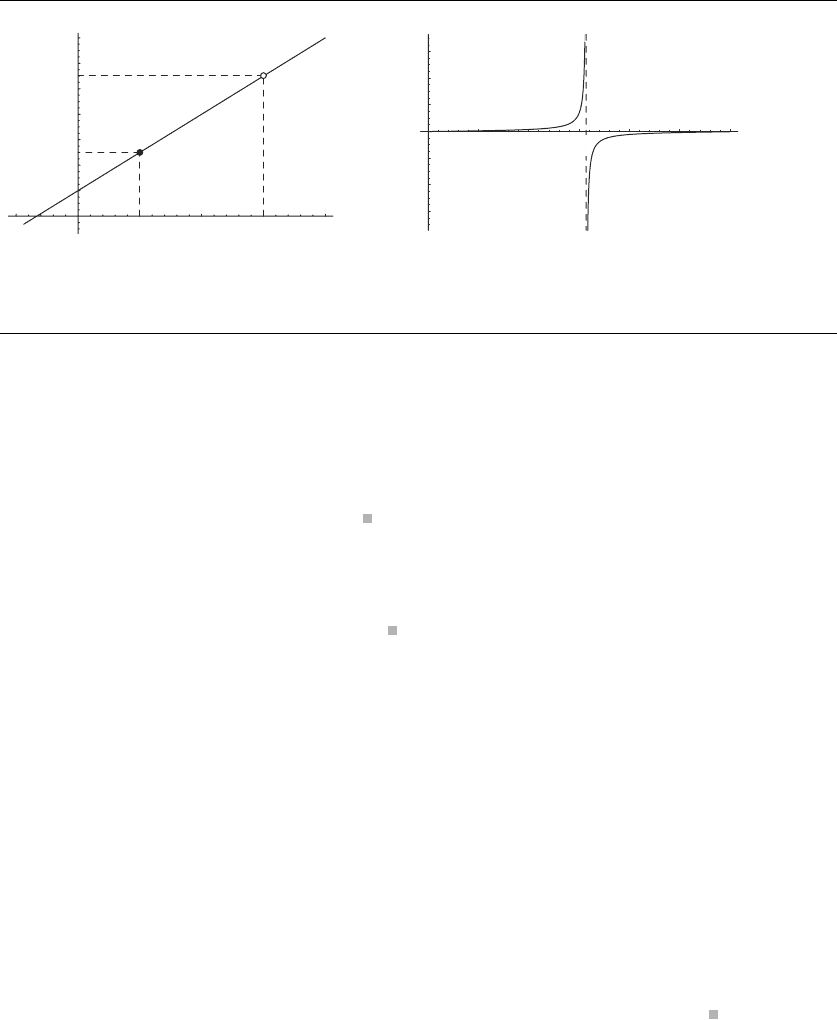
A.9 Topics from Calculus 899

0.5 1 2 2.5 3

–60

–40

–20

–1 1 2 3 4

f(x) = 3x + 2, 1 ≤ x < 3

Not closed on the right

f(x) = tan x, 0 ≤ x < 3

Not continuous

1.5

Figure A.6 Two functions that violate the assumptions of the Extreme Value Theorem.

Deﬁnition

A.2

A number M is called an absolute minimum value for a function f with domain D if

i. f(x)≥ M, ∀x ∈D.

ii. ∃x ∈ D|f(x)= M.

Often, we are interested in extrema in some restricted portion of the domain of f .

Theorem A.1 Extreme Value Theorem—One-Variable Form: Let f(x)be continuous on the closed

interval [a, b]; then, there are numbers x

, x

∈ [a, b] such that f(x)≤ f(x

) and

f(x)≥ f(x

), ∀x ∈ [a, b].

Note that the two conditions—that f be continuous and that the interval be

closed—are both essential for guaranteeing the existence of relative extrema. Two

examples, each of which violates one of the conditions, respectively, are tan(x), ∀x ∈

[0, 3], and f(x)= 3x +2, ∀x ∈[2, 6). The tangent function fails to be continuous at

the value 1.5, and the line function fails because it is not closed on the right (there is

no “largest value less than 11”); graphs of these functions are shown in Figure A.6.

The Extreme Value Theorem merely deﬁnes the conditions under which extrema

exist—it does nothing directly to help ﬁnd them. For this, we must turn to the concept

of critical points.

Deﬁnition

A.3

For function f ,acritical point is any point x ∈D such that either

i. the ﬁrst derivative is 0 − f



(x) = 0or

ii. the ﬁrst derivative does not exist

The critical points where f



(x) = 0 are known as stationary points.

900 Appendix A Numerical Methods

(a) (b)

(c)

(d)

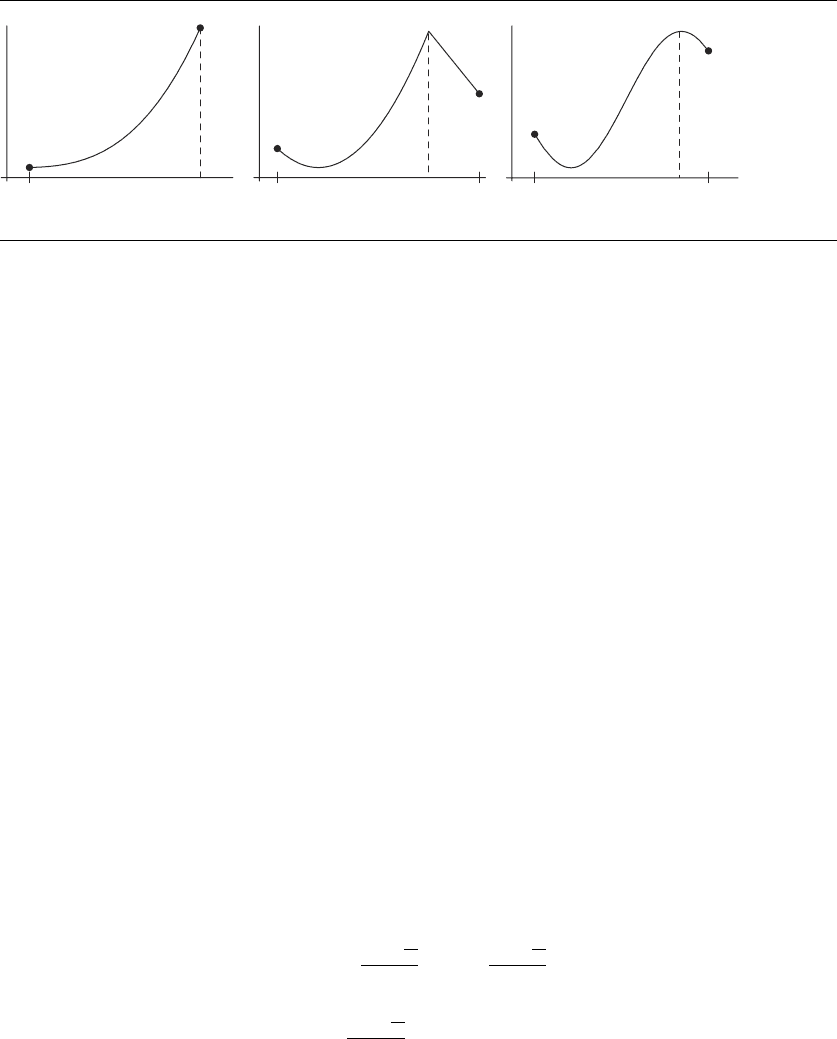
Figure A.7 A variety of functions, showing critical points—(a) and (b) are stationary points;

Figure A.7 shows a variety of critical points. Those in Figure A.7(a), A.7(b),

and A.7(c) are stationary points; the critical points in Figure A.7(c) and A.7(d) are

also called inﬂection points. Critical points are signiﬁcant because they are key to

determining the extrema, as the following theorem states.

Theorem A.2 If a function f has an extremum on an interval (a, b), then the extremum occurs at

a critical point of f .

A proof of this theorem can be found in Anton (1980). This theorem can be

usedtolocateanextremumoff on closed intervals as well: the extremum occurs

either within the interval or at one of the boundaries. Figure A.8 shows intervals of

functions at which the maximum occurs at the right end, within the interval at a

A.9 Topics from Calculus 901

= b x

aa abb

Figure A.8 The maximum of a function may occur at the boundary of an interval or within the

interval.

point at which f is not differentiable, and within the interval at a point at which f

is differentiable. Thus, an effective procedure to ﬁnd the extrema of a (continuous)

function f on a closed interval [a, b]is

1. Find the critical points in the open interval (a, b).

2. Evaluate f at the interval boundaries a and b.

3. Compare the values of the critical points and the interval boundaries. The small-

est among them is the minimum, and the largest is the maximum.

An example should demonstrate this. Consider the equation

f(x)= x

+ 6x

− 7x + 19 (A.10)

We wish to ﬁnd the extrema on the interval [−8, 3] (see Figure A.9). First, we must

verify that the function is continuous in order for the Extreme Value Theorem to

apply, but this function is a polynomial and so we know it is continuous. Our theorem

tells us that if there is an extremum in the open interval, it must occur at a critical

point, and as critical points (in this case) must occur where the derivative is zero, we

must solve f



(x) to ﬁnd these points.

The derivative of f is



(x) = 3x

+ 12x −7 (A.11)

whose roots are {{x →

−6−

√

}, {x →

−6+

√

}}≈{−4.51661, 0.516611} (see Fig-

ure A.10). The values of f at the end points are f(−8) =−53, f(3) = 79. The mini-

mum therefore occurs at the left boundary f(−8) =−53, and the maximum occurs

at the critical point f(

−6−

√

) ≈ f(−4.51661) ≈ 80.8771.

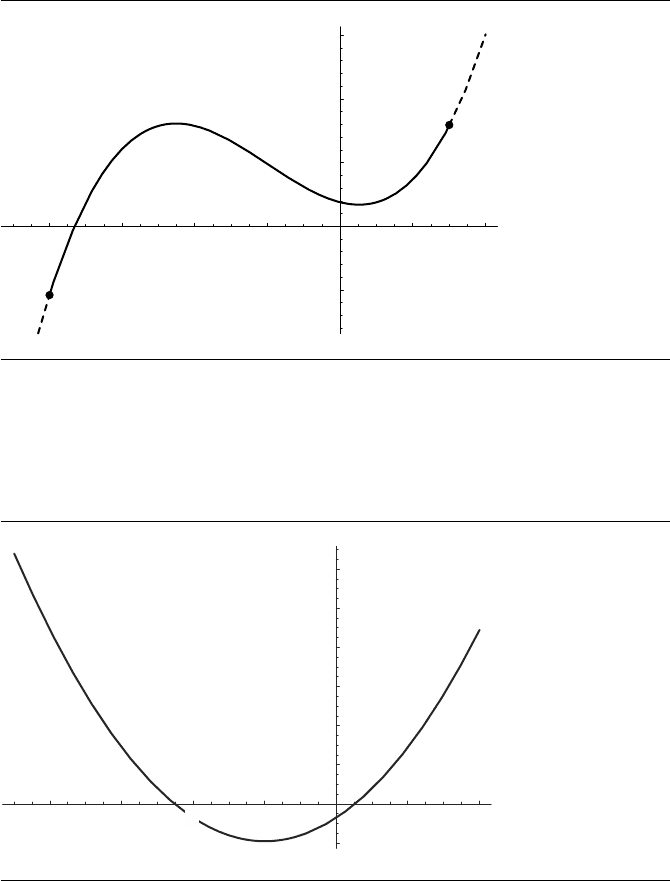
902 Appendix A Numerical Methods

–8 –6 –4 –2 2 4

–50

100

150

Figure A.9 f(x)= x

+ 6x

− 7x + 19, ∀x ∈[−8, 3].

–8 –6 –2 2 4

–20

100

120

–4

Figure A.10 f



(x) = 3x

+ 12x −7, ∀x ∈[−8, 3].

A.9 Topics from Calculus 903

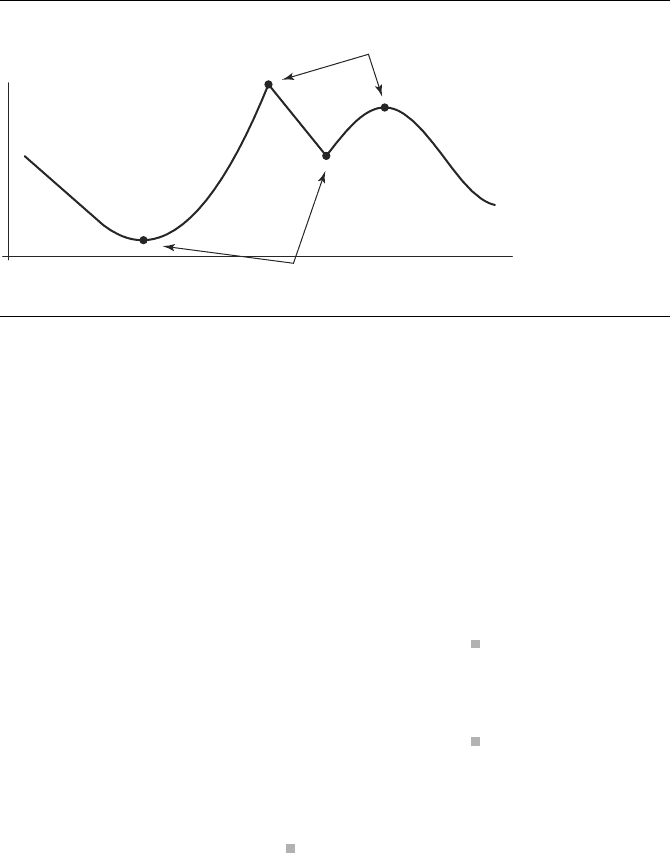
Relative maxima

Relative minima

Figure A.11 Relative extrema.

Relative Extrema

The Extreme Value Theorem applies only when the interval is closed and when the

function is continuous. So, there are cases in which it cannot be applied. The graphs

of many functions contain intervals that contain what we may informally refer to

as “hills” and “valleys”—these are called relative extrema; an example is shown in

Figure A.11. These characteristics are deﬁned formally as follows

Deﬁnition

A.4

A function f has a relative maximum at x

∃(a, b)|f(x

) ≥ f(x), ∀x ∈(a, b)

Deﬁnition

A.5

A function f has a relative minimum at x

∃(a, b)|f(x

) ≤ f(x), ∀x ∈(a, b)

Three theorems allow us to identify relative extrema.

Theorem A.3 Relative Extreme Value Theorem: If a function f hasarelativeextremumatapoint

, then x

is a critical point for f .

Note that this does not work the other way—a critical point may or may not be

an extremum at all; Figure A.7(c) has a critical point that is not a relative extremum.

Theorem A.4 First Derivative Test: If a function f is continuous at a critical point x

, then

i. If f



(x) > 0 within an (open) interval extending left from x

and f



(x) < 0 within

that interval, extending right from x

, then f(x

) is a relative maximum.