Schneider P., Eberly D.H. Geometric Tools for Computer Graphics

Подождите немного. Документ загружается.

904 Appendix A Numerical Methods

–1 1 3 4 5 6

–15

–10

–5

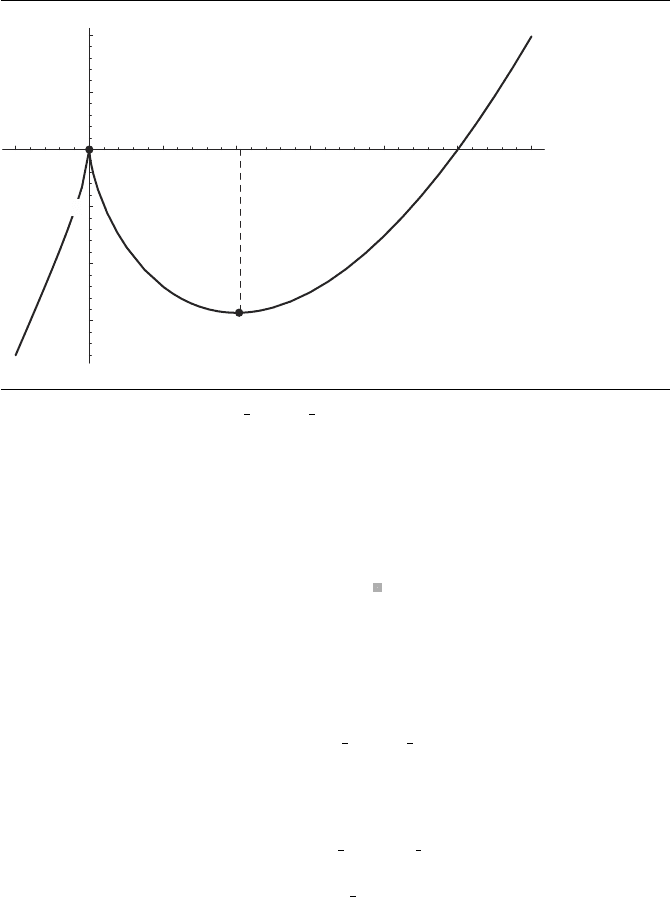
Figure A.12 Relative extrema of f(x)= 3x

− 15x

ii. If f



(x) < 0 within an (open) interval extending left from x

and f



(x) > 0 within

that interval, extending right from x

, then f(x

) is a relative minimum.

iii. If f



(x) has the same sign within an (open) interval both to the left and right of

, then f(x

) is not a relative extremum.

Informally, the relative extrema of such functions occur at critical points where

the derivative changes sign.

An example from Anton (1980) shows how this theorem can be used to ﬁnd the

relative extrema of the function

f(x)= 3x

− 15x

We take the derivative of f to ﬁnd the critical points:



(x) = 5x

− 10x

−

= 5x

−

(x −2)

The critical points, then, are x = 0 (where the derivative does not exist), and x = 2

(see Figure A.12).

The third theorem is the following

Theorem A.5 Second Derivative Test: If f is twice differentiable at a stationary point x

, then

A.9 Topics from Calculus 905

i. If f



)>0, then f(x

) is a relative minimum.

ii. If f



)<0, then f(x

) is a relative maximum.

The intuition for this theorem is as follows: The graph of the function at a crit-

ical point where the second derivative is negative is “concave up.” The graph of the

function at a critical point where the second derivative is positive is “concave down.”

An example shows how this works. We wish to ﬁnd the local extrema of

f(x)= x

− 3x

+ 3

We take the ﬁrst derivative to ﬁnd the critical points:



(x) = 4x

− 6x

which are

{{x →−1.22474}, {x → 0}, {x → 1.22474}}

The second derivative is



(x) = 12x

− 6

If we plug in the stationary points of f



into f



we get



(−1.22474) = 12 > 0



(0) =−6 < 0



(1.22474) = 12 > 0

and so we can conclude that there is a relative maximum at x =0 and relative minima

at x ≈−1.22474 and x ≈1.22474.

Functions of More than One Variable

In the previous subsection, we presented techniques for ﬁnding the extrema of func-

tions of one variable; here, we describe analogous techniques for functions of two

variables. Single-variable functions are conveniently visualized as curves in the plane,

and in an analogous fashion, two-variable functions can be visualized as surfaces in

3D space. As surfaces are the 3D analogs of curves, so too we have techniques for

optimization that extend those used for curves.

As with the graphs of single-variable functions, the “hills and valleys” of the

graphs of two-variable functions are the relative extrema (see Figure A.13). This is

formalized with the following deﬁnitions.

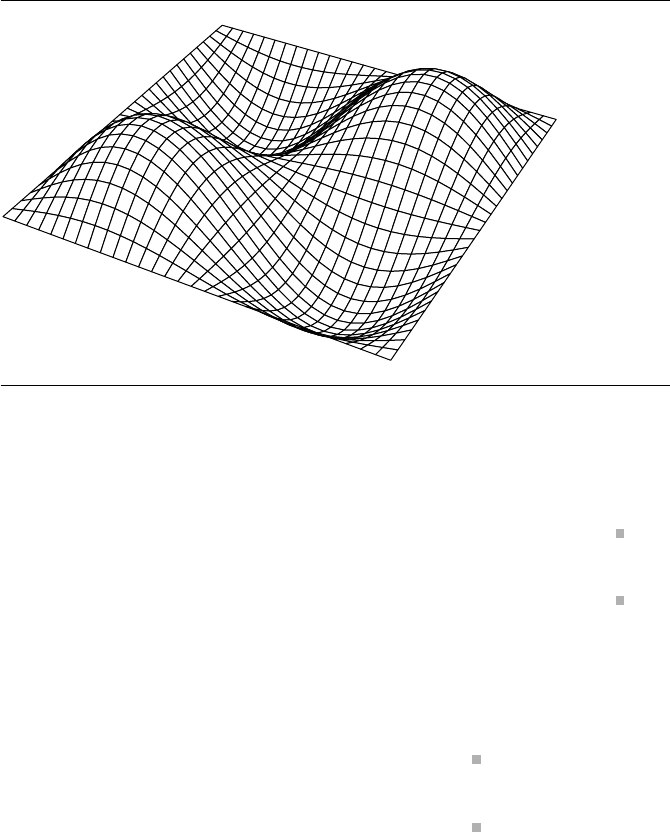
906 Appendix A Numerical Methods

Figure A.13 Relative extrema of a function of two variables are the hills and valleys of its graph.

Deﬁnition

A.6

A function f of two variables has a relative maximum at a point (x

, y

) if there is a

circle with center (x

, y

) such that f(x

, y

) ≥ f(x, y), ∀x inside the circle.

Deﬁnition

A.7

A function f of two variables has a relative minimum at a point (x

, y

) if there is a

circle with center (x

, y

) such that f(x

, y

) ≤ f(x, y), ∀x inside the circle.

This idea of the circle can be understood to be the natural generalization of the

linear interval of the domain of a single-variable function.

Deﬁnitions for absolute extrema are the following.

Deﬁnition

A.8

A function f of two variables with domains D

and D

has an absolute maximum at

a point (x

, y

) if f(x

, y

) ≥ f(x, y), ∀(x, y) ∈D

× D

Deﬁnition

A.9

A function f of two variables with domains D

and D

has an absolute minimum at

a point (x

, y

) if f(x

, y

) ≤ f(x, y), ∀(x, y) ∈D

× D

For a one-variable function, a relative extremum exists where the ﬁrst derivative is

zero; on the graph, this is depicted by the tangent being horizontal. For two-variable

functions, the analogous condition is that we have a relative extremum at a point

where the partial derivatives with respect to x and y are both zero (provided they

exist); graphically, this can be seen in that the traces of the graph of z = f(x, y) on

the planes x =x

and y = y

have horizontal tangent lines at (x

, y

) (Figure A.14).

Thus, we have

A.9 Topics from Calculus 907

x = x

y = y

, y

)

Relative

maximum

Figure A.14 The relative maximum of a function z = f(x, y). After Anton (1980).

∂f

∂x

, y

) = 0

and

∂f

∂y

, y

) = 0

This is formalized in the following theorem.

Theorem A.6

If a two-variable function f has a relative extremum at (x

, y

), and if the ﬁrst partial

derivatives of f both exist at that point, then

∂f

∂x

, y

) = 0

and

∂f

∂y

, y

) = 0

908 Appendix A Numerical Methods

Just as with one-variable functions, points in the domain of a function f(x, y)

with partial ﬁrst derivatives equal to zero are called critical points, and so the theo-

rem echoes the analogous one for one-variable functions in stating that the relative

extrema of functions occur at critical points.

Recall that for a one-variable function, the ﬁrst derivative being zero does not

guarantee that the point is a relative extremum; the example was an inﬂection point in

the graph of the function. Similarly, for two-variable functions, the partial derivatives

being both zero do not guarantee you have a relative extremum. Figure A.15 shows

the graph of the function f(x, y) = x

− y

. At the point (0, 0), the traces of the

function in both the XZ and YZ planes have horizontal tangent lines because

∂f

∂x

, y

) = 0

∂f

∂y

, y

) = 0

Observe that any circlecenteredat(0, 0) will have points that have a z-value greater

than 0 and points that have a z-value less than zero, and so (0, 0), in spite of being

a critical point, is not an extremum. Not surprisingly, such points are called saddle

points.

We can use the ﬁrst partial derivatives to locate relative extrema and saddle points

of functions. For example, given the function

f(x, y) = 3 − x

− y

we take the partial derivatives

∂f

∂x

=−2x

∂f

∂y

=−2y

and set them to zero. This yields x = 0 and y = 0, and so (0, 0) is the only critical

point. Evaluating the function at this critical point, we get f(0, 0) = 3; for all points

(x, y) other than (0, 0),wehavef(x, y) < 3 because f(x, y) = 3 − x

− y

= 3 −

+ y

). Thus, (0, 0) is a relative maximum for f .

For single-variable functions, we have a second derivative test (Theorem A.5) that

we can apply for more complex functions. For two-variable functions, we have an

analogous theorem.

Theorem A.7 Second Partials Test: Suppose we have a function f with a critical point at (x

, y

), and

which has continuous second partial derivatives in some circle around that point. If

we let

A.9 Topics from Calculus 909

Figure A.15 A “saddle function”—the point (0, 0) is not an extremum, in spite of the ﬁrst partial

derivatives being zero.

D =

∂

∂x

, y

)

∂

∂y

, y

) − (

∂

∂y∂x

, y

))

then the following hold:

i. If D>0 and

∂

∂x

, y

)>0, then f has a relative minimum at (x

, y

ii. If D>0 and

∂

∂x

, y

)<0, then f has a relative maximum at (x

, y

iii. If D<0, then f has a saddle point at (x

, y

iv. If D =0, then there are no conclusions to be drawn.

As an example, consider the function

f(x, y) = 2y

x −yx

+ 4xy

We begin by ﬁnding the ﬁrst partials:

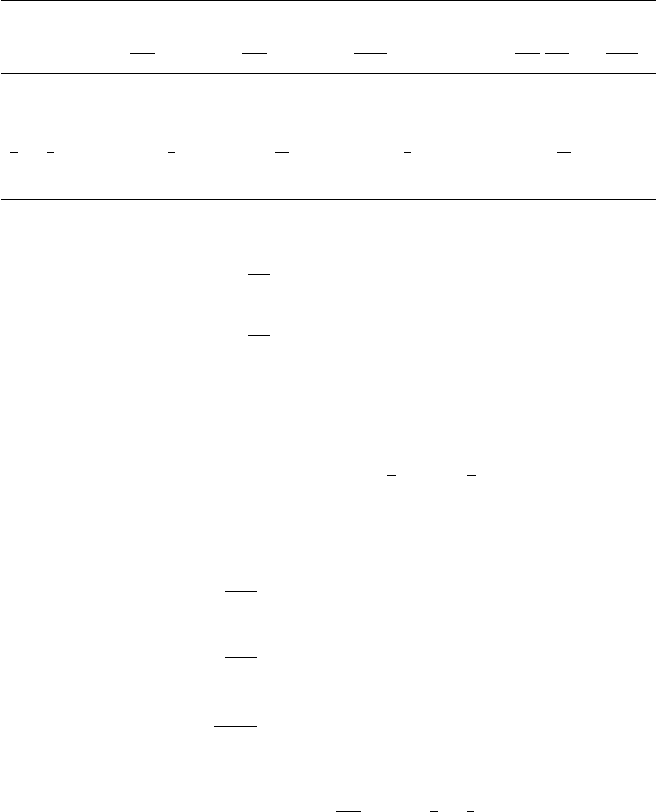
910 Appendix A Numerical Methods

Table A.10 Second partials of f(x, y) = 2y

x −yx

+ 4xy at critical points.

Critical point

, y

)

∂

∂x

, y

)

∂

∂y

, y

)

∂

∂y∂x

, y

)D=

∂

∂x

∂

∂y

− (

∂

∂y∂x

)

(0, −2) 40−4 −16

(0, 0) 00−4 −16

(

, −

)

−

(4, 0) 016−4 −16

∂f

∂x

= 4y − 2xy + 2y

∂f

∂y

= 4x − x

+ 4xy

If we take the right-hand sides of these and solve them simultaneously for x and y,

we get

{{x →0, y →−2}, {x → 0, y →0}, {x →

, y →−

}, {x → 4, y → 0}}

The second partial derivatives are

∂

∂x

(x, y) =4y −2xy + 2y

∂

∂y

(x, y) =4x −x

+ 4xy

∂

∂y∂x

(x, y) =4 −2x +4y

For convenient analysis, see Table A.10 We have D<0at(0, −2), (0, 0), and (4, 0),

and so these are saddle points; D>0 and

∂

∂x

> 0at(

, −

), and so this is a relative

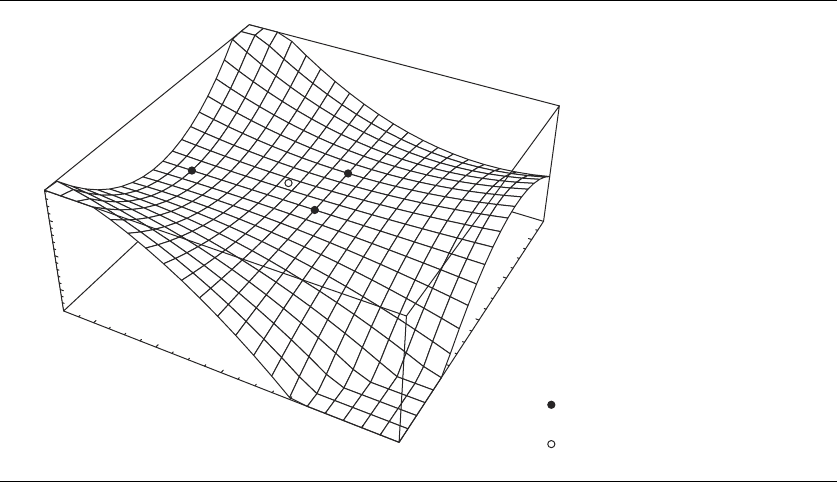
minimum. The surface is shown in Figure A.16, and its contour plot is shown in

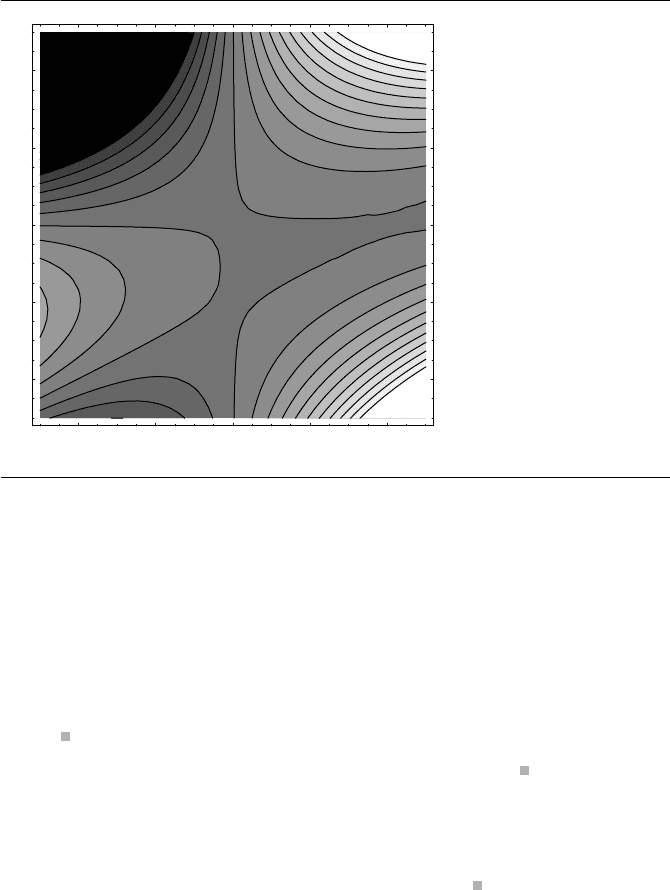
Figure A.17.

A.9.3 Lagrange Multipliers

Geometric problems frequently involve ﬁnding minima or maxima of an equation;

schemes for solving these problems are discussed in Section A.9.2. In this section we

A.9 Topics from Calculus 911

–4

–2

–100

100

–4

–2

Saddle points

Relative minimum

Figure A.16 Graphof2y

x −yx

+ 4xy, showing saddle points and relative minimum.

cover a particular type of these problems, which involve ﬁnding minima or maxima

subject to a constraint. The canonical forms for these problems are the following.

Two-Variable Extremum Problem with One Constraint: Maximize or minimize the

function

f(x, y)

subject to the constraint

g(x, y) = 0

Three-Variable Extremum Problem with One Constraint: Maximize or minimize

the function

f(x, y, z)

subject to the constraint

g(x, y, z) = 0

912 Appendix A Numerical Methods

–4 –2 0 2 4

–4

–2

Figure A.17 Contour plot of 2y

x −yx

+ 4xy.

Constrained extremum problems can be thought of as a restriction on the domain of

f(x, y).

Note that the extremum may be at one end or the other of the interval, or any-

where in between. Now, we need an analogous deﬁnition for functions of two vari-

ables. First, a couple of deﬁnitions.

Deﬁnition

A.10

A closed set is one that contains all of its boundary points; for example, on a closed

curve.

Deﬁnition

A.11

A bounded set is one whose members can be enclosed by a disk.

We are now able to proceed.

Theorem A.8 Extreme Value Theorem—Two-Variable Form: Let D be a closed and bounded set, and

let f(x, y) be continuous on it; then, there are points (x

, y

), (x

, y

) ∈ D such that

f(x, y) ≤ f(x

, y

) and f(x, y) ≥ f(x

, y

), ∀(x, y) ∈D.

The constraint equation can be solved for one of the variables in terms of the

rest, and the result substituted into the extremum equation. Then, the techniques

described in Section A.9.2 can be applied (also, we have to plug in the boundary

points as well, in case they are the extrema). However, this may not be feasible—

the constraint equation can be too complex. In such cases, the method of Lagrange

multipliers can be applied.

A.9 Topics from Calculus 913

Theorem A.9 Constrained-Extremum Principle—Two-Variable Form: Let f and g be two-variable

functions with continuous ﬁrst partial derivatives on some set D containing the curve

g(x, y) =0, with ∇g =0 at any point on that curve. Suppose that f has a constrained

extremum on the constraint curve; then this extremum occurs at the point (x

, y

and the gradients of f and g are parallel at that point:

∇f(x

, y

) = λ∇g(x

, y

), λ ∈ R

The number λ is called a Lagrange multiplier.

This may not necessarily seem obvious at ﬁrst, so here’s a less formal explanation.

From Section A.9.1, we know that the gradient of f is perpendicular to the tangent

vector of f :

∇f(x

, y

) · (x



)i + y



)j) = 0

If we assume that (x

, y

) is indeed an extremum, then it lies on the constraint curve

g(x, y) = 0.

But of course, ∇g(x

, y

) is also perpendicular to g(x, y) at (x

, y

) because it is

the level curve for function g. Thus, ∇f(x

, y

) and ∇g(x

, y

) are both perpendic-

ular to the constraint curve at (x

, y

), and therefore both of their tangent vectors are

parallel. Put more directly, the curves are tangent at the extrema.

A simple example can illustrate this. Suppose we have an ellipse with the equation

E :15x

+ 7y

+ 11xy = 30

and wish to ﬁnd the point on the ellipse closest to the origin (0, 0). That is, we wish to

minimize the distance function



+ y

, subject to the constraint that (x, y) ∈ E.

The set E is closed and bounded, so by Theorem A.8 we know that there is some

point P ∈ E such that f(P)≤ f (Q), ∀Q ∈ E.

We want to minimize

f(x, y) = x

+ y

(we use the squared distance to avoid an otherwise unneccessary square root call)

subject to the constraint

g(x, y) = 17x

+ 8y

+ 12xy = 100

By Theorem A.9, we must have

∇f = λ∇g