Соболев А.Б., Рыбалко А.Ф. Математика курс лекций для технических университетов
Подождите немного. Документ загружается.

Ряды Фурье
131
кратных дуг:
()
1
sin .
n
n
f
xb
∞
=
=⋅
∑
nx
2). Если функция f(x) четная, f(-x) = f(x), все коэффициенты b
n
равны
нулю, b
n
=0, так как при этом функция
(
)
sin
f
xnx
⋅
– нечетная.
Функция
(
)
cos
f
x⋅ nx
при этом четная,
()
0
0
2
,afx
π
π
=
∫
dx
()
0
2
cos ,
n
afxnx
π
π
=
∫
dx и ряд Фурье четной периодической функции со-
держит только
косинусы кратных дуг:
()
0
1
cos .
2
n
n
a
f
xa
∞
=
=+
∑
nx
16.2. Ряд Фурье для функции с произвольным
периодом Т=2l
По условию
(
)
(
)
2
f
xl fx+=
.
Сделаем замену переменной, ,
l
x
t
π
= tx
l
π
= .
Тогда
()
l
f
xf t
π
⎛⎞
==
⎜⎟
⎝⎠
2
l
f
tl
π
⎛⎞
+
=
⎜⎟
⎝⎠
2
l
f
tx
t
π
π
⎛⎞
+
⋅=
⎜⎟
⎝⎠
=
2ll
f
tt
t
π
π
π
⎛⎞
+⋅
⎜⎟
⎝⎠
()
2
l
ft
π
π
⎛⎞
=+
⎜⎟
⎝⎠
.
Функция
()
l
f
xf t
π
⎛⎞
=
⎜
⎝⎠
⎟
по аргументу t имеет период 2π.
Разложим периодическую функцию с периодом 2π
l
f
t
π
⎛
⎜
⎝⎠
⎞
⎟
в ряд
Фурье на отрезке
[
]
,
π
π
−
.
()
0
1
cos sin ,
2
nn
n
a
l
f
tantb
π
∞
=
⎛⎞
=+ +
⎜⎟
⎝⎠
∑
nt
где ко-
эффициенты находятся по формулам:
0
1
;
l
aft
π
π
ππ
−
⎛⎞
=
⎜⎟
⎝⎠
∫
dt
1
cos ;
n
l
aftn
π
π
ππ
−
⎛⎞
=
⎜⎟
⎝⎠
∫
tdt
Лекции 15 - 16
132
1
sin .
n
l
bftn
π
π
ππ
−
⎛⎞
=
⎜⎟
⎝⎠
∫
tdt
Возвращаясь к старой переменной
;tx dt dx
ll
,
π
π
== получаем ряд Фурье
для функции с периодом 2L:
()
0
1
cos sin ,
2
nn
n
ann
f
xaxb
ll
ππ
∞
=
⎛⎞
=+ +
⎜⎟
⎝⎠
∑
x
где
()
0
1
;
l
l
afxdx
l
−
=
∫
()
1
cos ;
l
n
l
afxnx
ll
π
−
=
∫
dx
()
1
sin ;
l
n
l
n
bfx xdx
ll
π
−
=
∫
Пример:
Разложите в ряд Фурье функцию
(
)
f
xx
=
на отрезке
[
]
,ll−
.
Так как функция четная, b
n
=0,
0
0
2
,
l
axdx
l
l
=
=
∫
()
2
2
0
00
22 2
cos sin sin cos
l
ll
n
nlnln ln
ax xdx xx xdx
lllnlnll l
n
π
ππ
ππ
π
⎡⎤
== −=⋅
⎢⎥
⎢⎥
⎣⎦
∫∫
π
()
()
22
2
2
0, если четное,2;
2
4
cos cos 0
, если нечетное,2
21
п nk
l
l
n
п nk
n
k
π
π
π
−=
⎡
⎢
=−=
⎢
1.
−
=+
⎢
+
⎣
Итак,
22 2
24 1 1 5
cos cos3 cos ...
35
l
xxxx
ll l l
πππ
π
⎛⎞
=− + + +
⎜⎟
⎝⎠
[
,
]
;.
x
ll∈−
16.3. Разложение в ряд Фурье непериодических функций
Сумма ряда Фурье есть периодическая функция, поэтому неперио-
дическую кусочно-монотонную, заданную на интервале
функ-
цию нельзя представить рядом Фурье. Но можно разложить ее в ряд
Фурье на любом конечном промежутке.
(
,−∞ ∞
)
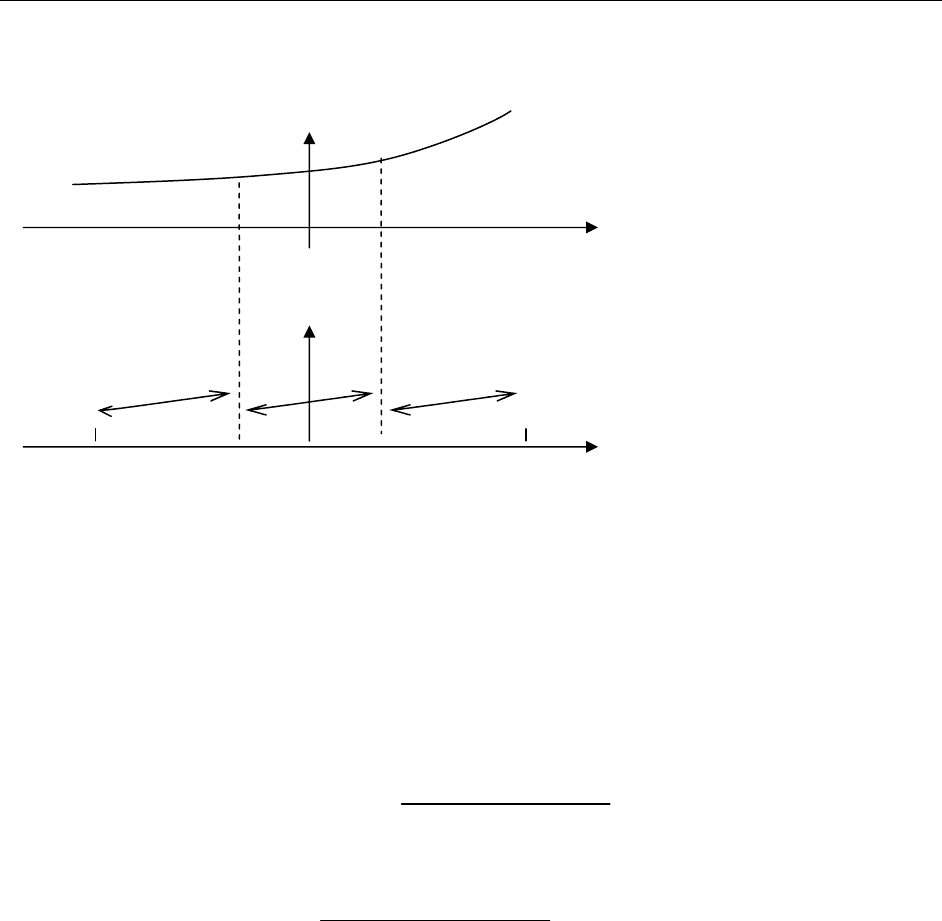
Ряды Фурье
133
Для функции f(x)
y f(x)
x
Построим функцию
(
)
x
ϕ
y
()
x
ϕ
x
-2l -l 0 l 2l
такую, что
(
)
(
)
x
fx
ϕ
=
для
(
)
;
x
ll
∈
−
, а на всю действительную ось она
продолжается периодически с периодом
: 2l
(
)
(
)
2.
x
xl
ϕ
ϕ
=
+
Функция
(
)
x
ϕ
разлагается в ряд Фурье (п. 15.5), причем в точках
x
l=±
выполняется:
()
(
)
(
)
00
,
2
ll
Sl
ϕϕ
−+ +
=
где
(
)
(
)
00,lfl
ϕ
−= −
(
)
(
)
(
)
00llfl0,
ϕ
ϕ
+
=−+=−+
то есть
()
(
)
(
)
00
,
2
fl f l
Sl
−+ −+
=
(
)
(
)
.Sl Sl
−
=
Итак, если
произвольная функция f(x) задана на интервале
(
)
0,l
,
ее можно представить в виде
периодической функции
(
)
x
ϕ
с периодом
, дополнив (продолжив) f(x) произвольным образом некоторой ку-
сочно-монотонной функцией
2l
(
)
1
f
x
на интервал
(
)
,0l
−
так, что:
()
(
)
(
)
() ( )
1
,0,
,,
;
0.
f
xx l
x
fx x l
ϕ
∈
⎡
=
⎢
∈−
⎢
⎣
Так как продолжение
(
)
xf
1
первоначально заданной функции f(x)
может быть выбрано бесчисленным множеством способов, то сущест-
вует бесчисленное множество рядов Фурье, которые сходятся к f(x) в
интервале
(
)
0,l
.
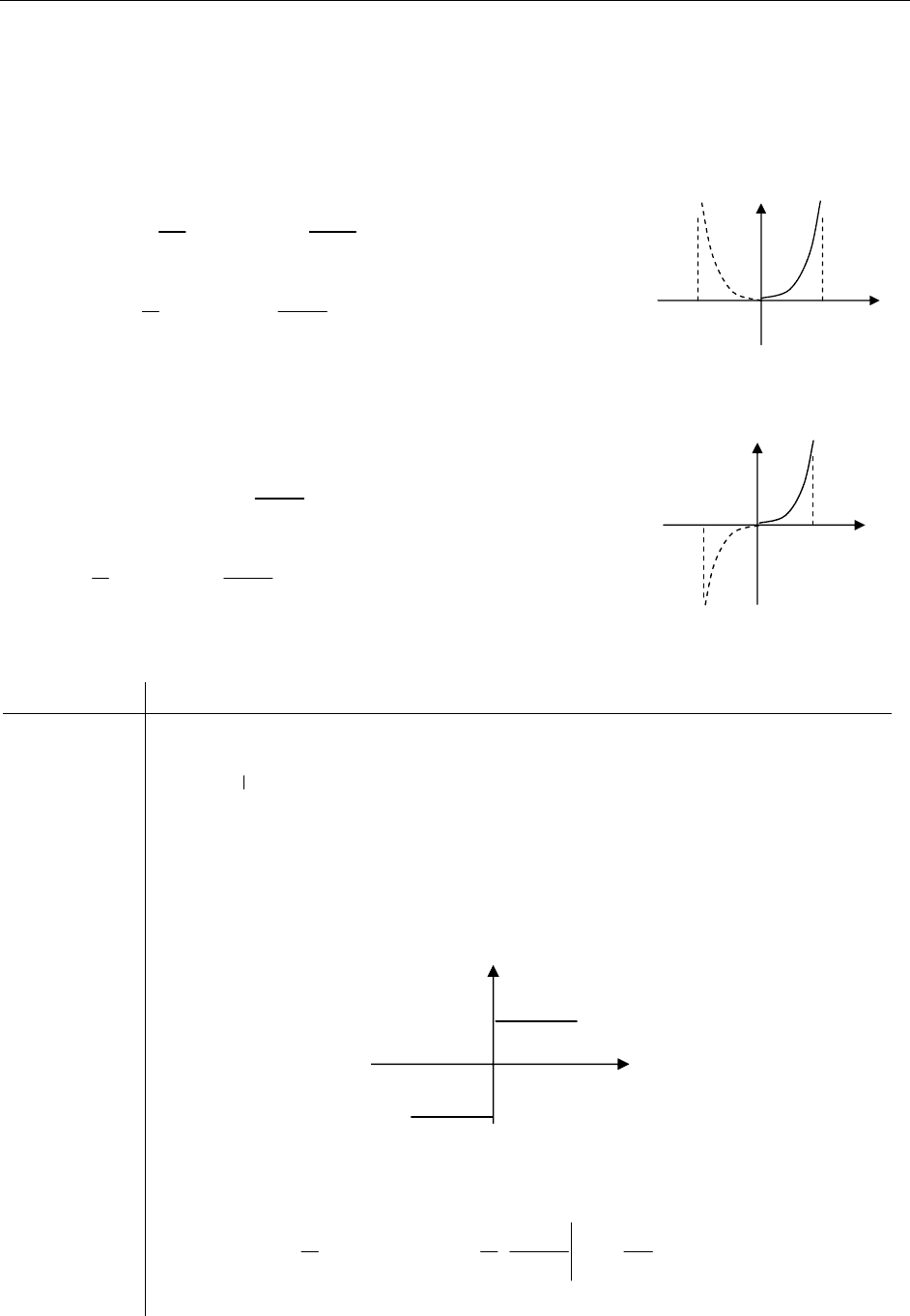
Лекции 15 - 16
134
Среди различных продолжений f(x) выберем четное и нечетное
продолжения, в результате которых получатся разложения f(x) либо по
косинусам, либо по синусам кратных дуг соответственно.
1.
Если
(
)
(
)
(
)
1
,,fx f x x l=− ∈−0,
то
()
0
1
cos ,
2
n
n
an
fx a
l
x
π
∞
=
=+
∑
где
()
0
2
cos ,
l
n
nx
afx dx
ll
π
=
∫
-l 0 l x
f
1
(x) y f(x)
(
)
0, ,
x
l
∈
1, 2, ...n =
y f(x)
f
1
(x)
-l 0 l x
Если
(
)
(
)
(
)
1
,,fx f x x l=− − ∈ − 0,
то
()
1
sin ,
n
n
nx
fx b
l
π
∞
=
=
∑
() ()
0
2
sin , 0,
l
n
nx
bfx dxx
ll
π
=∈
∫
l
Пример:
Разложите f (x)=1, заданную на интервале (0,π), по синусам и ко-
синусам кратных дуг.
Решение:
1).
()
.,,0
π
π
=
∈
lx
Продолжим f(x) на интервал (-π, 0) нечетным образом:
тогда
,
0=
n
a
()
0
0
22cos2
1sin cos 1
n
nx
bnxdx n
nn
π
π
π
πππ
=⋅ =−⋅ =− −
∫
=
y
1
-1
-π 0 π x
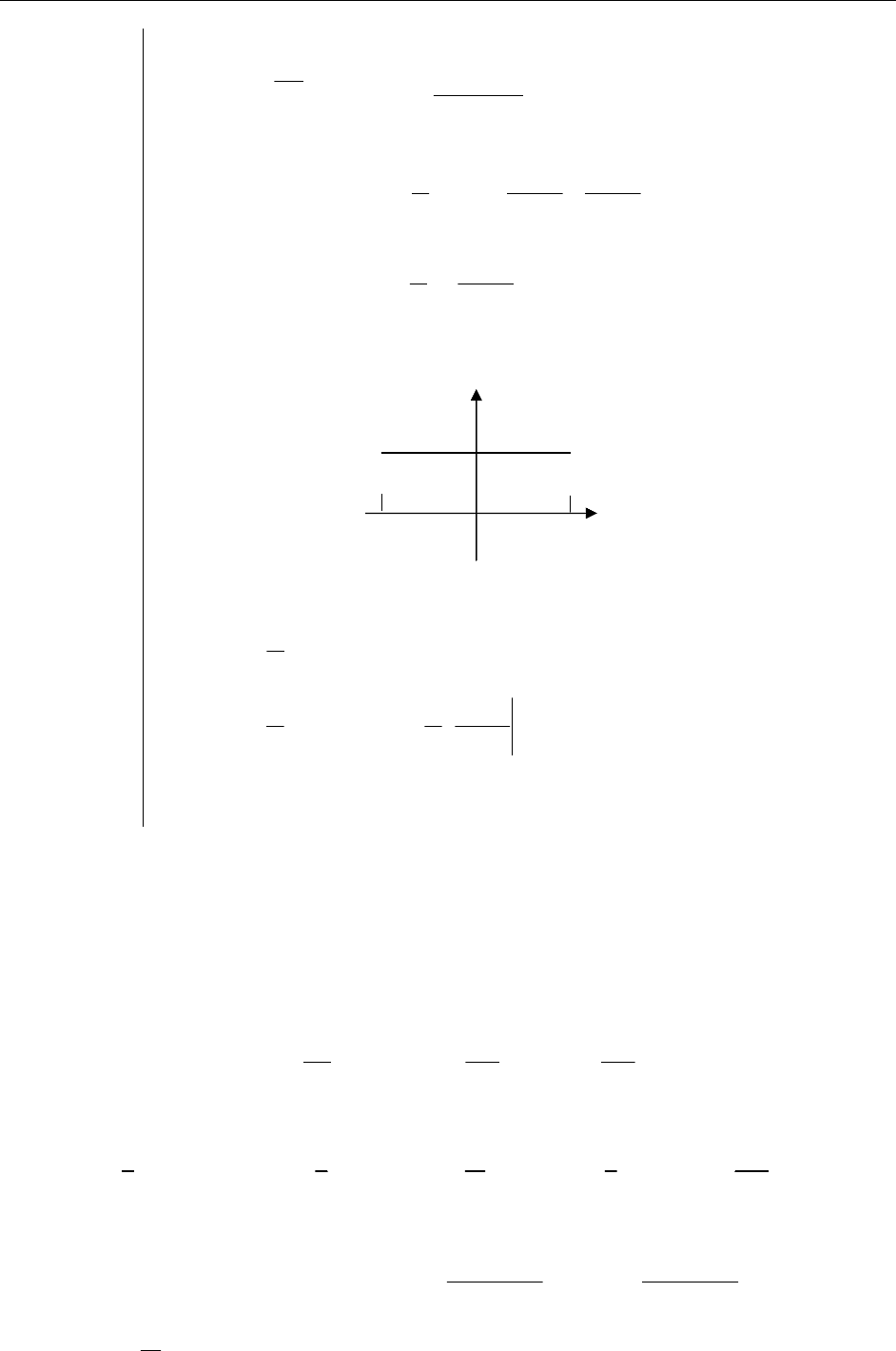
Ряды Фурье
135
()
()
()
0, если 2 четное,
2
4
11
, если 21нечетное.
21
n
п k
п k
n
k
π
π
=
⎡
⎢
=− − − =
⎢
=+
−
⎢
⎣
Итак,
=
⎟
⎠
⎞
⎜
⎝
⎛
+++= ...
5
5sin
3
3sin
sin
4
1
xx
x
π
()
∑
∞
=
−
−
=
1
:12sin
12
14
k
xk
k
π
2). Продолжим f (x) на интервал (-π,0) четным образом,
тогда
0=
n
b
∫
=⋅=
π
π
0
0
,21
2
dxa
0
sin2
cos1
2
0
0
=⋅=⋅=
∫
π
π
ππ
n
nx
dxnxa
n
и
∑
∞
=
=⋅+=
1
.1cos011
n
nx
-π 0 π x
y
16.4. Комплексная форма ряда Фурье
Ряд Фурье для функции
(
)
f
x
с периодом имеет вид: 2l
()
0
1
cos sin ,
2
nn
n
a
nn
f
xaxb
ll
x
π
π
∞
=
⎛⎞
=+ +
⎜⎟
⎝⎠
∑
где
()
0
1
;
l
l
afxdx
l
−
=
∫
()
1
cos ;
l
n
l
afxnx
ll
π
−
=
∫
dx
()
1
sin
l
n
l
n
bfx xdx
ll
π
−
=
∫
.
Преобразуем его к комплексной форме с помощью формул Эйлера:
cos sin
i
ei
ϕ
ϕ
ϕ
=+
, cos
2
ii
ee
ϕϕ
ϕ
−
+
=
,
sin
2
ii
ee
i
ϕ
ϕ
ϕ
−
−
=
.
Обозначим
l
π
ω
= .
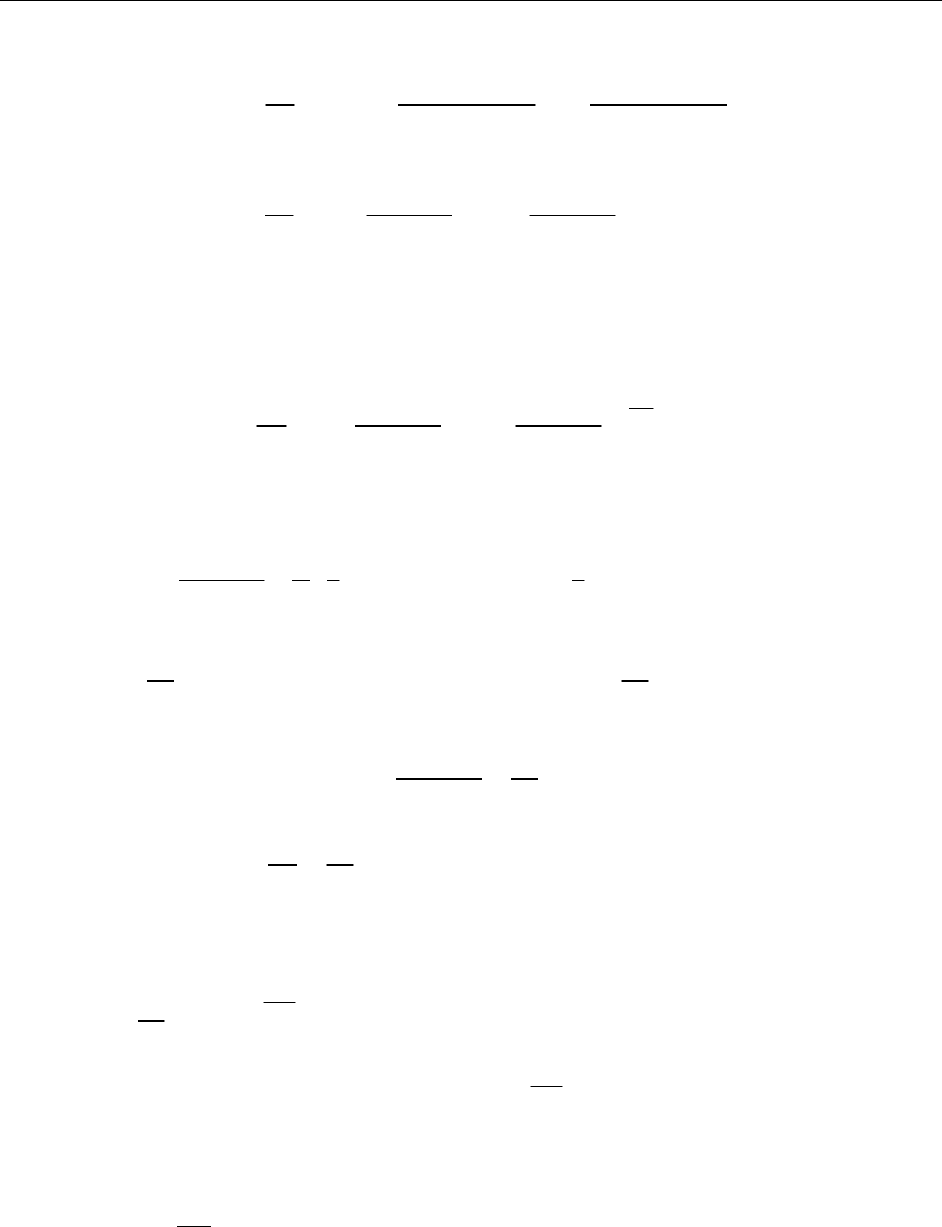
Лекции 15 - 16
136
Тогда
()
0
1
222
in x in x in x in x
nn
n
a
ee ee
fx a b
i
ωω ωω
−−
∞
=
⎛⎞
+−
=+ +
⎜⎟
⎝⎠
∑
=
0
1
22 2
in x in x
nn nn
n
aaibaib
ee
ωω
∞
−
=
−+
⎛⎞
=+ +
⎜⎟
⎝⎠
∑
,
или
, где введены обозначения:
()
(
0
1
in x in x
nn
n
fx c ce ce
ω
∞
−
−
=
=+ +
∑
)
ω
Nnc
iba
c
iba
c
a
c
n
nn
n
nn
n
∈=
+
=
−
==
−
,
2
,
2
,
2
0
0
.
Получим выражения для комплексных коэффициентов
и :
n
c
n
c
−
() ()
11 1
cos sin
22
ll
nn
n
ll
aib
с fx nxdx i fx nxdx
ll
ωω
−−
⎛⎞
−
== −
⎜⎟
⎝⎠
∫∫
=
()() () ()
11
cos sin .
22
ll
in x
ll
f
xnxinxdxfxe
ll
ω
ωω
−
−−
=−+−=
⎡⎤
⎣⎦
∫∫
dx
Аналогично для
n
c
−
имеем
1
()
22
l
in x
nn
n
l
aib
cfxe
l
ω
−
−
+
==
∫
1,2,...n =
dx
, где
При
имеем 0n =
0
0
1
()
22
l
l
a
cf
l
−
==
∫
xdx
.
Если считать номер
не натуральным, а целым числом, ,
n
0, 1, 2, ...n =±±
все формулы для вычисления коэффициентов ряда можно записать единооб-
разно:
1
()
2
l
in x
l
n
l
cfxedx
l
π
−
−
=
∫
0, 1, 2, ...n
,
=
±±
, а сам ряд Фурье в виде
()
in x
l
n
n
f
xce
π
∞
=−∞
=
∑
.
Эта сумма называется
рядом Фурье в комплексной форме, слагающие ее
функции
in x
l
n
ce
π
- комплексными гармониками, коэффициенты
- комплексными амплитудами гармоник.
n
c

Ряды Фурье
137
Пример:
Разложить в комплексный
ряд Фурье периодическую
функцию
()
f
x
с периодом
2π, если на
[
]
;
π
π
−
.
()
[
]
()
1, 0, ;
1, , 0 .
x
fx
x
π
π
⎡
∈
=
⎢
−∈−
⎢
⎣
Решение:
Вычислим комплексные коэффициенты Фурье:
0
1
() 0
2
cfxdx
π
π
π
−
=
=
∫
;
0
0
11
() () ()
22
inx inx inx
n
c f xe dx f xe dx f xe dx
ππ
ππ
ππ
−−
−−
⎛⎞
== +
⎜⎟
⎝⎠
∫∫∫
−
=
0
000
11
22
in in
inx inx inx
ee
edx edx edx
ni
πππ
ππ
π
ππ
−
−
−− −
−
⎛⎞⎛⎞
+−
=− + = + =
⎜⎟⎜⎟
−
⎝⎠⎝⎠
∫∫ ∫∫
2
2
π
=
()
0, 2 ,
1cos
.
2
,21,
21
nm
n
mZ
nm
ni
im
π
π
π
=
⎡
−
⎢
==
⎢
=+
+
⎢
⎣
∈
Выпишем разложение
(
)
fx
:
()
(
)
()
21
2
21
im x
m
e
fx
im
π
+
∞
=−∞
=
=
+
∑
3355
2
...
35
ix ix ix ix
ix ix
ee ee
ee
i
π
−−
−
⎛⎞
−−
=−+ + +
⎜⎟
⎝⎠
=
3355
4
...
23252
ix ix ix ix ix ix
ee e e e e
iii
π
−− −
⎛⎞
−− −
=+++
⎜⎟
⋅⋅
⎝⎠
=
(
)
0
sin 2 1
4 sin sin 3 sin 5 4
... .
13 5 21
n
nx
xxx
n
ππ
∞
=
+
⎛⎞
=+++=
⎜⎟
+
⎝⎠
∑
Как видно, по комплексной форме ряда Фурье легко восстанавли-
вается его обычный вид (обычное разложение было получено ра-
нее, стр.132).

Лекции 15 - 16
138
16.5. Интеграл Фурье
Функцию
(
)
f
x
, удовлетворяющую на отрезке
[
]
;ll
−
условиям тео-
ремы Дирихле, можно разложить в ряд Фурье:
()
()
0
1
cos sin
2
nnnn
n
a
f
xakxb
∞
=
=+ +
∑
kx
;
где
()
1
cos
l
nn
l
afxkxdx
l
−
=
∫
,
(
)
0,1, 2,...n
=
;
()
1
sin
l
nn
l
bfxkxdx
l
−
=
∫
,
(
)
1,2,...n
=
,
и введено обозначение:
n
n
k
l
π
= (так называемые волновые числа).
Функция
(
)
f
x
может быть периодической с периодом или непе-
риодической. В последнем случае предполагается, что с отрезка
2l
[
]
;ll
−
на всю числовую ось функция продолжена периодически.
Рассмотрим случай, когда непериодическая функция задана на всей чи-
словой оси
(
)
;−∞ ∞
, на любом конечном отрезке
[
]
;ll
−
удовлетворяет усло-
виям теоремы Дирихле и
абсолютно интегрируема на всей числовой
оси, т.е.
()
fxdx M
∞
−∞
=<∞
∫
.
Подставим в ряд значения коэффициентов
и :
n
a
n
b
() () ()
()
1
11
cos cos sin sin
2
ll
nn nn
n
ll
f
x f tdt f t kx kt kx ktdt
ll
∞
=
−−
=+ +
∑
∫∫
=
() () ( )
1
11
cos cos
2
ll
nn
n
ll
f
tktdt ft kxt
ll
∞
=
−−
=+⋅
∑
∫∫
dt−.
Устремим
к бесконечности. Предел первого слагаемого l
() () ()
11 1
lim lim lim lim 0
22 2
ll
lll l
ll
M
f t dt f t dt f t dt
ll l
∞
→∞ →∞ →∞ →∞
−− −∞
≤≤ =
∫∫ ∫
2l
=
.
Преобразуем второе слагаемое (сумму):

Ряды Фурье
139
() ( )
()
11
11
cos
l
nn
nn
l
f
tkxtdt Fk
ll
∞∞
==
−
⋅−=
∑∑
∫
, где
()
() ( )
cos
l
nn
l
Fk f t k x tdt
−
=⋅ −
∫
(этот интеграл зависит и от
x
, но в данном случае нас интересует толь-
ко зависимость от волновых чисел
).
n
k
Заметим, что волновые числа
n
n
k
l
π
= образуют арифметическую про-
грессию с разностью
n
k
l
π
∆=, причем
lim 0
n
l
k
→∞
∆
=
. Это позволяет преоб-
разовать сумму:
() () ()
11 1
11 1
nn n
nn n
n
F
kFk Fk
ll
π
ππ
∞∞ ∞
== =
==
∑∑ ∑
k⋅∆
;
последнее представление позволяет рассматривать ряд как интеграль-
ную сумму:
()
()
1
0
11
lim
nn
n
n
Fk k Fkdk
ππ
∞
∞
→∞
=
⋅∆ =
∑
∫
,
или
() () () ( )
00
11
cos
f
xFkdkdkftkxt
ππ
∞∞∞
−∞
==
∫∫∫
dt−.
Эта формула называется
формулой Фурье, а интеграл, стоящий в
правой части, –
интегралом Фурье. Функция
(
)
Fk
называется спек-
тральной плотностью
.
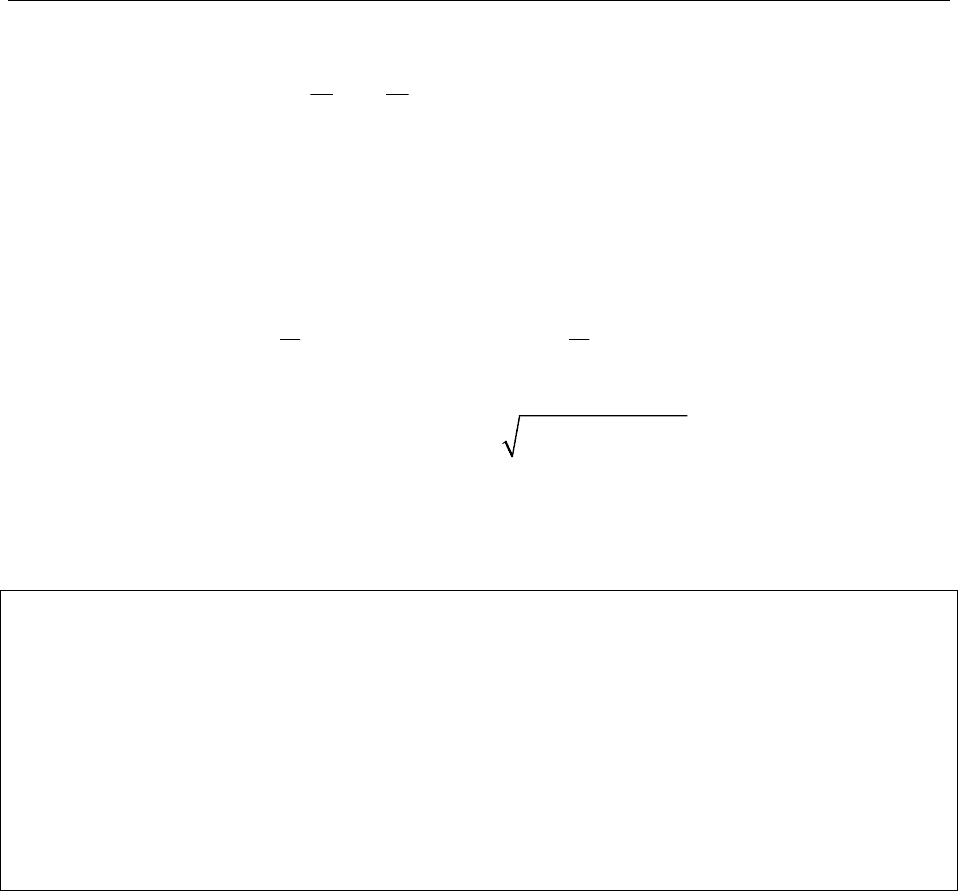
Это название связано со следующими обстоятельствами: для пе-
риодической функции
(
)
f
x
с периодом набор величин 2l
2
nn
Dab=+
2
n
показывает, в какой мере в разложении функции
(
)
f
x
представлены различные гармоники
cos
nx
l
π
, sin
nx
l
π
и называется
спектром функции
(
)
f
x
.
Для периодической функции
(
)
f
x
спектр - функция целочисленно-
го аргумента, т.е. последовательность, величины отдельных членов ко-
торой показывает вклад соответствующих гармоник (
(
)
f
x
составляется
как сумма бесконечного, но
счетного количества гармоник). Для непе-
риодической функции
(
)
f
x
в разложении ее на простейшие периодиче-
ские составляющие присутствует
несчетное количество слагаемых (ин-
Лекции 15 - 16
140
теграл), величина
(
)
Fk k∆
описывает вклад гармоник с волновыми чис-
лами из интервала
()
22
;
kk
kk
∆∆
−+
.
Интеграл
Фурье можно представить в виде, подобном ряду Фурье:
() () ()
()
0
cos sin
f
xAkkxBkkx
∞
=+
∫
dk,
где
()
() ( )
()
11
cos , sin
A
k f t ktdt B k f t ktdt
ππ
∞∞
−∞ −∞
==
∫∫
,
и введенные ранее амплитуды
() () ()
22
Dk A k B k=+
.
В результате изучения материала, изложенного в этих лекциях,
студент должен знать:
определение тригонометрического ряда и ряда Фурье данной периодической
функции;
достаточные условия разложимости функции в ряд Фурье (условия Ди-
рихле);
особенности разложений четных и нечетных функций;
разложение в ряд Фурье функций произвольного периода;
представление непериодической функции рядом Фурье.
