Соболев А.Б., Рыбалко А.Ф. Математика курс лекций для технических университетов
Подождите немного. Документ загружается.


Кратные интегралы
11
2. Фигура – часть плоскости xOy, D
Φ
↔
,
(
)
(
)
,
f
Pfxy
=
, ddS
µ
=
,
(
)
(
)
,
D
f
Pd f xydS
Φ
µ
=
∫∫∫
– двойной интеграл от функции
(
)
(
)
,
f
Pfxy=
по области D.
3. Фигура –
пространственная область, G
Φ
↔
,
(
)
(
)
,,
f
Pfxyz= ,
ddV
µ
= ,
(
)
(
)
,,
G
f
Pd f xyzdv
Φ
µ
=
∫∫∫∫
– тройной интеграл от функции
(
)
(
)
,,
f
Pfxyz= по области G.
4. Фигура –
линия на плоскости или в пространстве,
L
Φ
↔
,
()
(
)
()
,
,,
f
xy
fP
f
xyz
⎧
⎪
=
⎨
⎪
⎩
, ddl
(
)
(
)
,,
L
f
Pd f xyzdl
Φ
µ
=
∫
∫
,
µ
= – криволинейный
интеграл от функции
(
)
f
P по кривой L.
5. Фигура –
поверхность,
Φ
↔
∑
,
(
)
(
)
,,
f
Pfxyz
=
, dd
µ
σ
= ,
(
)
(
)
,,
f
Pd f xyzd
Φ
µ
σ
=
∑
∫∫∫
– поверхностный интеграл от функции
(
)
(
)
,,
f
Pfxyz= по области
∑
.
1.5. Свойства интегралов по фигуре,
определяемые равенствами
Доказательства свойств следуют из определения интеграла по фигуре.
Пусть интеграл по фигуре существует, тогда:
1.
(
)
(
)
cf P d c f P d
ΦΦ
µ
µ
=
∫∫
, с = const.
Доказательство:
() () () ()
00
11
lim lim
nn
nn
ii ii
rr
ii
сfPd cfP c fP cfPd
Φ Φ
µ
µµ
→→
==
=∆= ∆=
∑∑
∫∫
µ
.
2.
(
)
(
)
(
)
(
)
(
)
f
PgPd fPd gPd
ΦΦΦ
µ
µµ
±= ±
∫∫∫
2
.
3. Свойство аддитивности. Пусть фигура Ф состоит из двух частей, т.е.
1
ΦΦΦ
= ∪ , тогда
(
)
(
)
(
)
12
f
Pd f Pd f Pd
ΦΦΦ
µ
µµ
=+
∫∫∫
.
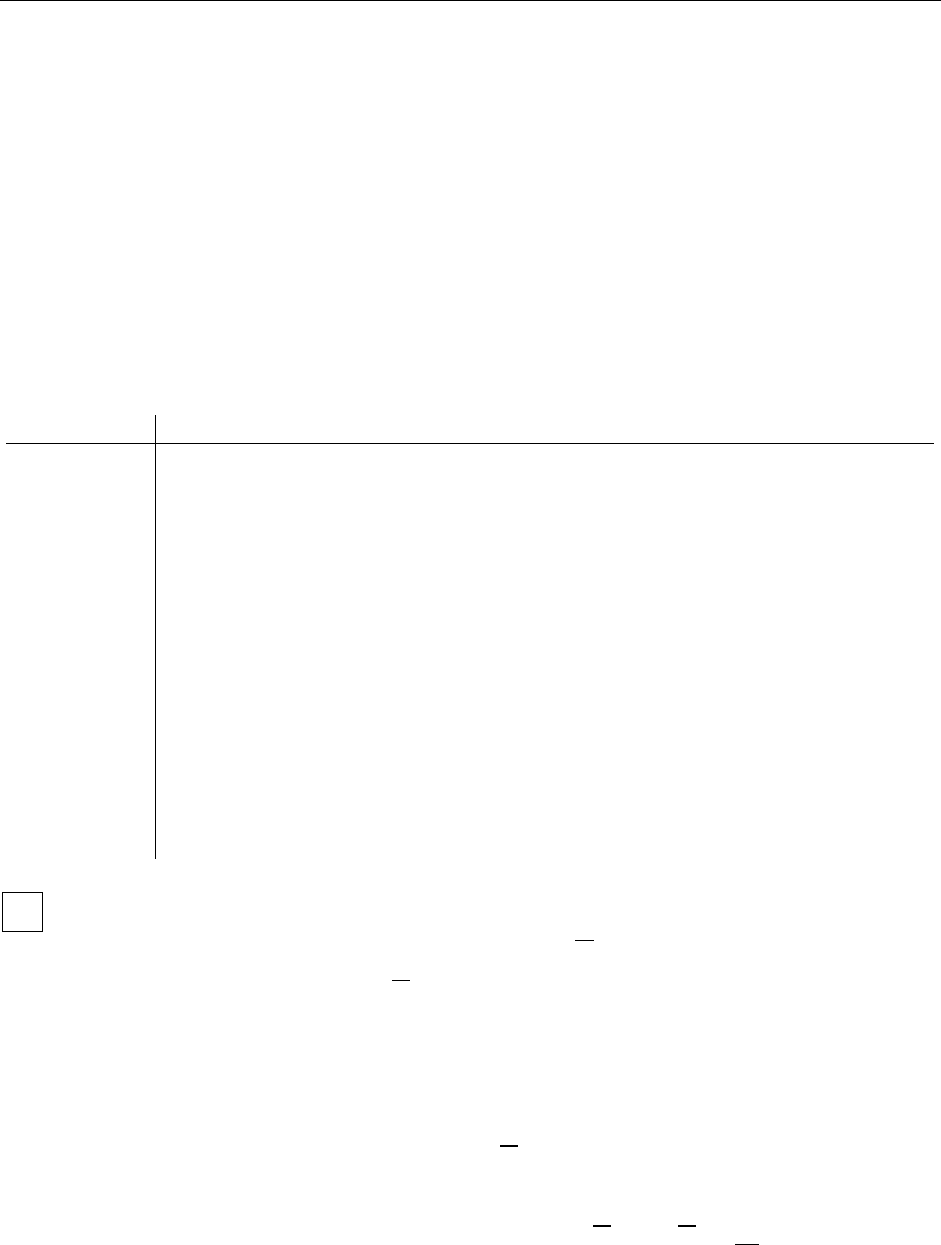
Лекция 1 - 4
12
1.6. Свойства интегралов по фигуре, определяемые
неравенствами (оценка интегралов по фигуре)
1. Если для любой точки
P Ф
∈
(
)
0fP≥ , то
(
)
0fPd
Φ
µ
≥
∫
.
2. Если для любой точки
P Ф
∈
(
)
(
)
f
PgP≥ , то
(
)
(
)
f
Pd gPd
ΦΦ
µ
µ
≥
∫
∫
.
3. Если существуют такие два числа
m, M, что
(
)
mfP M
≤
≤ , то
(
)
mfPdM
Φ
µ
µ
≤≤
∫
µ
, где
µ
−
мера Ф.
Пример:
1) .
() () ()
b
a
mb a f xdx M b a−≤ ≤ −
∫
2)
.
()
,
D
mS f x y dS MS≤≤
∫∫
3)
.
()
,,
G
mV f x y z dv MV≤≤
∫∫∫
4)
.
()
,,
L
mL f x y z dl ML≤≤
∫
5)
.
()
,,
пов пов
mS f x y z d MS
σ
≤≤
∑
∫∫
Теорема о среднем. Если функция
(
)
f
P непрерывна в замкнутой огра-
ниченной области
Ф, то существует точка
Т
P
Φ
∈
, такая, что выполняется
равенство:
()
(
)
f
Pd f P
Φ
µµ
=
∫
.
Физический смысл теоремы о среднем
Пусть фигура Ф обладает массой, распределенной с плотностью
(
)
(
)
f
PP
ρ
= , тогда
(
)
(
)
mfPd fP
Φ
µµ
==
∫
. В случае пространственной фи-
гуры мера фигуры равна объему
V
µ
=
,
(
)
mV P
ρ
= ,
()
m
P
V
ρ
= - среднее зна-
чение плотности.

Кратные интегралы
13
Геометрический смысл интегралов по фигуре
Пусть
(
)
1fP≡ , тогда интеграл по фигуре будет равен мере соответст-
вующей фигуры, т. е.
d
Φ
µ
µ
=
∫
. В частных случаях:
1.
- длина отрезка
[]
.
b
a
dx b a=−
∫
a,b
2.
- площадь области D.
D
dS S=
∫∫
3.
- объем пространственной области G.
G
dV V=
∫∫∫
4.
- длина линии L.
L
dl L=
∫
5.
- площадь поверхности
dS
σ
=
∑
∑
∫∫
∑
.
Механический смысл интегралов по фигуре
Если функция
() ()
f
PP
ρ
= является плотностью фигуры, то масса фи-
гуры выражается интегралом по фигуре
(
)
Ф
Pd m
ρµ
=
∫
.
2.1. Двойной интеграл. Геометрический смысл
двойного интеграла
Рассмотрим фигуру, которая является частью плоскости
xOy: .
Интеграл по фигуре в данном случае является двойным интегралом от функ-
ции
f(P)=
D
Φ
↔
(, )
f
xy по области D:
01
() lim ()
n
n
ii
ri
D
f
PdS f P S
→=
=
Σ∆
∫∫
.

Лекция 1 - 4
14
Задача о вычислении объема тела
Найдем объем тела, ограниченного сверху
непрерывной поверхностью (, )
zfxy
=
, снизу
замкнутой областью
D
плоскости
x
Oy и сбоку
цилиндрической поверхностью, образующие ко-
торой параллельны оси
Oz, а направляющей явля-
ется граница
Г области D .
Разобьем основание
D
на конечное число
элементарных ячеек
. В каждой
ячейке выберем точку
12
, ,...,
n
SS S∆∆ ∆
(, )
iii i
M
xy S
∈
∆ (1,2,...)in
=
и построим столбик с основанием
i
S
∆
и высотой
(, )
ii i i
M
Nfxy= .
Если приближенно принять каждый столбик
за прямой цилиндр, то в этом приближении его
объем равен
, а объем всего те-
ла приближенно равен
. Перейдем к пределу
(, )
iii
Vfxy S∆≈ ⋅∆
i
S∆
1
(, )
n
ii i
i
Vfxy
=
≈
∑
0
x
y
z
D
Γ
),( yxfz
=
0
x
y
z
i
N
i
M
i
S∆
0
1
lim ( , ) ( , ) ( )
n
n
ii i
r
i
DD
V f x y S f x y dS f P dS
→
=
=∑ ∆= =
∫∫ ∫∫
.
Вывод:
если (, ) 0
f
xy ≥ , то
(, )
D
f
xydS
∫∫
представляет объем криволинейного
цилиндра, построенного на области
D
и ограниченного сверху поверхностью
(, )
f
xy.
2.2. Вычисление двойного интеграла
Рассмотрим прямоугольную область интегрирования
;
. Найдем объем тела, ограниченного поверхностью ,
плоскостью 0
и цилиндрической поверхностью, образующие которой па-
раллельны оси
Oz, а направляющей служит граница области
{[,
Dxab=∈
]
[, ]}
ycd∈ (, )zfxy=
z =
D
.
Вычислим объем по площадям параллельных сечений.
Проведем плоскость ()
x
const a x b=<<
zfxy xconst== 0z
. Фигура, получающаяся в се-
чении, представляет собой криволинейную трапецию, ограниченную линия-
ми:
,
(,)( )
=
, yc
=
, yd
=
. Площадь сечения равна:
.
() (, )
d
c
Sx f xydy=
∫
Кратные интегралы
15
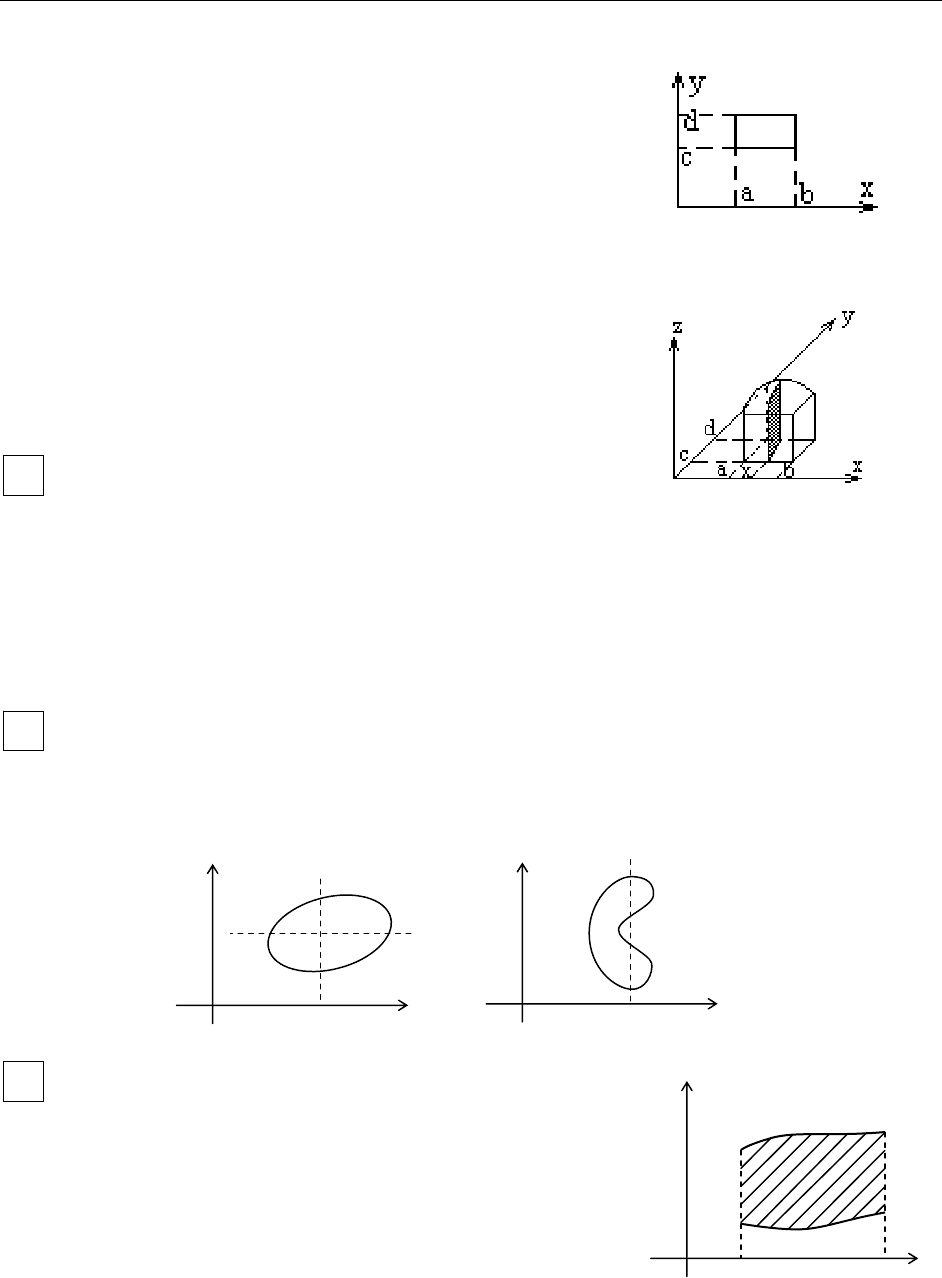
Объем всего тела равен
y
a
b
)(
1
xy
ϕ
=
x
0
D
)(
2
xy
ϕ
=
()
VSxdx==
(, )
bbd
aac
fxydydx
⎛⎞
⎜⎟
⎝⎠
∫∫∫
.
Ранее было показано, что объем такого тела ра-
вен двойному интегралу от (, )
f
xy по области D,
таким образом:
(, ) (, )
bd
Dac
f
xydxdy f xydy dx
⎛⎞
=
⎜⎟
⎝⎠
∫∫ ∫ ∫
.
Аналогично:
(, ) (, )
db
Dca
f
x y dxdy dy f x y dx=
∫∫ ∫ ∫
.
Запись двойного интеграла
(, ) (, )
bd
Dac
f
xydxdy f xydy dx
⎛⎞
=
⎜
⎝⎠
∫∫ ∫ ∫
⎟
называют
повторным интегралом, при этом
(, )
d
c
f
xydy
∫
- называют внутренним, а
∫
внешним интегралом. {...}
b
a
dx
!
Рассмотрим произвольную область интегрирования.
Область
D
в плоскости
x
Oy называется правильной в направлении
или
y
x
, если каждая прямая, параллельная соответствующей координат-
ной оси и проходящая через внутреннюю точку области, пересекает гра-
ницу области в двух точках.
О
0
y
x
D
неп
р
ав.
0
y
x
D
M
п
р
ав.
Т
Двойной интеграл от непрерывной функции
(, )
f
xy по правильной области равен
двукратному интегралу от этой функции по
области
D
D
.
Пусть
D
- правильная область в направле-
нии , ограниченная линиями: Oy
1
(yx)
ϕ
=
,
2
()yx
ϕ
=
,
x
a= ,
x
b= .
Тогда
2
1
()
()
(, ) (, )
x
b
Dax
f
xydxdy f xydy dx
ϕ
ϕ
⎛⎞
=
⎜⎟
⎜⎟
⎝⎠
∫∫ ∫ ∫
.

Лекция 1 - 4
16
Рассмотрение проводится аналогично предыдущему случаю; при этом
площадь сечения вычисляется так:
2
1
()
()
() (, )
x
x
Sx f xydy
ϕ
ϕ
=
∫
,
а объем всего тела: .
2
1
()
()
() (, )
x
bb
aax
V S x dx f x y dy dx
ϕ
ϕ
⎛⎞
==
⎜⎟
⎜⎟
⎝⎠
∫∫∫
Таким образом,
2
1
()
()
(, ) (, )
x
b
Dax
f
xydxdy f xydy dx
ϕ
ϕ
⎛⎞
=
⎜⎟
⎜⎟
⎝⎠
∫∫ ∫ ∫
.
Аналогично, если
D
- правильная область в направлении , ограни-
ченная линиями
Ox
1
()
x
y
ψ
=
,
2
()
x
y
ψ
=
, ,ycyd
=
= , то объем тела равен
2
1
()
()
(, ) (, )
y
d
Dcy
f
xydxdy f xydx dy
ψ
ψ
⎛⎞
=
⎜⎟
⎜⎟
⎝⎠
∫∫ ∫ ∫
.
!
1).
Правило вычисления двойных интегралов. Для того чтобы вычис-
лить двойной интеграл по произвольной правильной области
D
, необ-
ходимо свести его к повторному (двукратному) интегралу и проинтегри-
ровать функцию по одной из переменных в пределах, соответствующих
произвольному, но неизменному значению другой переменной, а затем
результат проинтегрировать в пределах ее полного изменения.
2). Представление двойного интеграла в виде двукратного зависит от
вида области
D
.
3). Порядок интегрирования может быть изменен в соответствии с ра-
венствами
22
11
() ()
() ()
(, ) (, ) (, )
xy
bd
Daxcy
f
x y dxdy dx f x y dy dy f x y dx
ϕψ
ϕψ
==
∫∫ ∫ ∫ ∫ ∫
.
4). Если область
D
неправильная, то ее разбивают на конечное число
правильных областей
i
D
и на основании свойств полагают, что двойной
интеграл по области
D
равен сумме двойных интегралов по облас-
тям
i
D
.
5). Внешний интеграл всегда вычисляется в постоянных пределах.
6). Если пределы интегрирования в повторном интеграле от непрерыв-
ной функции конечны и
постоянны, то результат не зависит от порядка
интегрирования.

Кратные интегралы
17
Пример:
Вычислите
, если область задана неравенствами:
∫∫
D
dxdyxy
2
D 10
≤
≤ x ,
.
32 ≤≤− y
Решение:
∫∫ ∫ ∫ ∫∫
−
−
=⋅==
⎟
⎠
⎞
⎜
⎝
⎛
+
=⋅==
D
x
dxx
y
xdxdyyxdxdxdyxy
1
0
3
2
1
0
1
0
2
3
2
1
0
3
22
6
35
2
1
3
35
23
35
3
827
3
или
∫∫ ∫ ∫∫∫
−
−
−−
=⋅=====
D
y
dyy
x
dyyxdxdyydxdyxy
3
2
3
2
3
3
2
2
1
0
3
2
2
2
1
0
22
6
35
3
35
2
1
32
1
2
1
2
.
Пример:
Вычислите
, где - треугольник с
вершинами:
, , .
∫∫
D
ydxdyx
2
D
)0,0(O )0,2(A )1,2(B
Решение:
Область , ограниченная прямыми: D 0
=
y ,
2
x
y =
, , является правильной. При фик-
сированном
2=x
x
изменяется от до y 0
2
x
:
5
4
58
1
8
1
2
2
0
5
2
0
4
2
0
2
0
2
2
2
0
2
0
22
=====
∫∫∫∫∫∫
∆
x
dxx
y
dxxydydxxydxdyx
x
x
OAB
.
O
1
1
2
y
x
A
B
x
Пример:
Изменить порядок интегрирования в повторном интеграле:
2
1
0
(, )
x
x
dx f x y dy
∫∫
.
Решение:
Область интегрирования D ограничена прямой
x
y =
и параболой и является правиль-
ной как в отношении оси Ox, так и Oy с верхней
границей
и нижней . Всякая пря-
мая, параллельная оси Ox, пересекает границу
области не более чем в двух точках, следова-
тельно, можно вычислить интеграл, полагая
внешние пределы интегрирования
2
xy =
y
=
x
2
xy =
1,0
=
=
yy .
При этом пределы во внутреннем интеграле бу-
дут иметь вид: нижний предел
1
x
y
=
, верхний
2
x
y=+ .
Таким образом:
() ()
2
11
00
y
x
y
x
dx f x,y dy dy f x, y dx=
∫∫ ∫∫

Лекция 1 - 4
18
Пример:
Расставить пределы интегрирования в двойном
интеграле, если область D – кольцо.
⎪
⎩
⎪
⎨
⎧
=+
=+
4
1
:
22
22
yx
yx
D
D – неправильная область.
Разобьем ее на четыре правильных области:
1234
... ... ... ... ....
DDDDD
=+++
∫∫ ∫∫ ∫∫ ∫∫ ∫∫
Границами правильных областей являются дуги соответствующих ок-
ружностей
2
1yx=± − ,
2
4yx
=
±− и прямые 1
x
=± .
1234
222
22 2
14 14 2 4 1 1
211 1
41 4 4
... ... ... ... ...
... ... ... ... .
DDDDD
xxx
xx x x
dx dy dx dy dx dy dx dy
−− − − −−
−− −
−− − −− −−
=+++=
=+++
∫∫ ∫∫ ∫∫ ∫∫ ∫∫
∫∫ ∫∫ ∫∫ ∫∫
2
2
x
Пример:
Найти площадь фигуры, ограниченной параболами
⎪
⎩
⎪
⎨
⎧
=
=
xy
xy
D
2
:
Решение:
Полагаем ; (, ) 1fxy≡
∫∫ ∫∫
==
DD
dSdSyxf ),(
(
)
2
2
11
00
x
x
x
D
x
dxdy dx dy y dx
=
==
∫∫ ∫ ∫ ∫
()
1
1
111
3
22
2
0
000
0
21
33
x x dx xdx x dx x x=− = − =−=
∫∫∫
3
1
3
.
2.3. Замена переменных в двойном интеграле
В некоторых случаях вычисление двойных ин-
тегралов значительно упрощается, если изменить
область интегрирования, осуществив замену пере-
менных в двойном интеграле.
Рассмотрим (, )
D
f
xydxdy
∫
∫
. Если координаты
x
и являются функциями новых переменных и
:
y u
v
(,),
(,),
x
xuv
yyuv
=
⎧
⎨
=
⎩
то каждой точке (, )
M
xy на плоскости
x
Oy однозначно соот-
ветствует точка (,)
M
uv
′
на плоскости , а числа и называются кри-
волинейными координатами
точки
uOv u v
M
.
0
v
∆
u∆
D
′
v
u

Кратные интегралы
19
При этом область
D
отобразится в область
на плоскости , и каждому значению D
′
uOv
(, )
f
xy в области
D
соответствует то же значение
(,) ((,), (,))
f
uv f xuv yuv= в области D
′
.
Разбиение области на прямоугольные
площадки приводит к разбиению области
D
′
D
на
криволинейные четырехугольники с вершинами
, ,
, , где
111
(, )Px y
222
(, )Px y
333
(, )Px y
444
(, )Px y
1
(,)
x
xuv= ,
2
(,)
0
v
u
x
y
1
P
2
P
3
P
4
P
Duu ∆+ vv
∆
+
x
xu uv
=
+∆
3
(,)
x
xu uv v
=
+∆ +∆, ,
4
(, )
x
xuv v=+∆, ,
1
(,)yyuv=
2
(,yyu uv)
=
+∆ ,
3
(,yyu uv v)
=
+∆ +∆ ,
.
4
(, )yyuvv=+∆
Заменяя приращения функций (,)
x
uv и соответствующими диф-
ференциалами по формуле
(,)yuv
(,)(,)
f
f
f
uuvvfuv v
vu
u
∂
∂
+
∆+∆≈ +∆+∆
∂∂
, можно
считать, что
1
(,)
x
xuv= ,
2
(,)
x
x
xuv u
u
∂
=
+∆
∂
,
3
(,)
x
x
x
xuv u v
uv
∂∂
=
+∆+∆
∂∂
,
4
(,)
x
x
xuv v
v
∂
=+∆
∂
1
(,)yyuv=, ,
2
(, )
y
yyxy u
u
∂
=
+∆
∂
3
(,)
yy
yyuv u v
uv
∂∂
=
+∆+∆
∂∂
, ,
4
(,)
y
yyuv
v
∂
=+
∂
v∆. Четырехугольник при этом можно рассматривать как па-
раллелограмм. Его площадь
34 32
43 23
3432
[]
xx xx
SPPPP
yyyy
−−
=
×=
−−
=
3432 3234
()( )()( )xxyy xxyy
=
−−−−−=
xxyxyy
uvvvuv
uvvvuv
∂∂∂∂∂∂
⎛⎞⎛
=∆+∆∆−∆ ∆+∆
⎜⎟⎜
∂∂∂∂∂∂
⎝⎠⎝
⎞
=
⎟
⎠
xy xy
uv uv
uv vu
∂∂ ∂∂
⎛⎞
=∆∆−∆∆=
⎜⎟
∂∂ ∂∂
⎝⎠
xx
xy xy
uv
uv uv
yy
uv vu
uv
∂∂
∂∂ ∂∂
⎛⎞
∂∂
−
∆∆ = ∆∆
⎜⎟
∂∂
∂∂ ∂∂
⎝⎠
∂∂
.
Определитель
x
x
uv
J
yy
uv
∂∂
∂∂
=
∂∂
∂∂
называется якобианом преобразования.

Лекция 1 - 4
20
Предельный переход при неограниченном возрастании числа разбиений
области для соответствующих интегральных сумм приводит к формуле пре-
образования координат в двойном интеграле:
(, ) ((,), (,))| |
DD
f
x y dxdy f x u v y u v J dudv
′
=
∫∫ ∫∫
, где
x
x
uv
J
yy
uv
∂∂
∂∂
=
∂∂
∂∂
.
Пример:
Вычислите
, если область зада-
на уравнениями
∫∫
−
D
dxdyxy )( D
1
+
=
xy
,
3
−
=
xy
,
3
7
3
+−=
x
y
,
5
3
1
+−= xy
.
Решение:
Сделаем замену переменных:
⎪
⎩
⎪
⎨
⎧
+=
−=
,
3
,
x
yv
xyu
тогда област
D
′
будет зада-
ваться прямым
ь
и:
5
=v
. Для вычисления якобиана преоб-
разования выразим
,
3
7
,3,1 =−== vuu
x
и y через иu v :
vux
4
3
4
3
+−=
,
vuy
4
3
4
1
=
.
+
При этом
4
3
16
3
16
9
4
3
4
1
4
3
4
3
−=−−=
−
=
∂
∂
∂
∂
∂
∂
∂
∂
=
v
y
u
y
v
x
u
x
J
и =−
∫∫
D
dxdyxy )(
∫∫ ∫ ∫∫∫
′
−
′
−===⋅
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
+−−
⎟
⎠
⎞
⎜
⎝
⎛
+=
DD
ududvududvdudvvuvu
5
37
1
3
8
4
3
4
3
4
3
4
3
4
3
4
3
4
1
.
u
D
′
v
1
0
5
3
−
3
7
2.4. Двойной интеграл в полярных координатах
Перейдем в полярную систему координат cos
x
ρ
ϕ
=
, siny
ρ
ϕ
= и вы-
числим якобиан перехода: Если
u
ϕ
=
, v
ρ
=
, cos
x
ρ
ϕ
=
, siny
ρ
ϕ
= , то
22
cos sin
cos sin
sin cos
xx
J
yy
ϕρϕ
ρϕ
ρ
ϕρ ϕρ
ϕρ ϕ
ρϕ
∂∂
−
∂∂
== =+
∂∂
∂∂
=
,
и
(, ) ( cos , sin )
DD
f
xydxdy f d d
ρ
ϕρ ϕ ρ ρϕ
′
=⋅
∫
∫∫∫
