Соболев А.Б., Рыбалко А.Ф. Математика курс лекций для технических университетов
Подождите немного. Документ загружается.

Теория поля
71
OZ
0
(, )
2
nOZ
π
<
;
cos ddxdy
γ
σ
=
. Переходя к двойному интегралу по D
xy
:
, получим
xy
DΣ
→
∫∫ ∫∫
1
(, ,) (, ,)
xy
xx
D
axyz z axyz
I
dxdy
zy y
⎡⎤
∂∂∂
⎛⎞
=− −
⎜⎟
⎢⎥
∂∂ ∂
⎝⎠
⎣⎦
∫∫
.
По формуле дифференцирования сложной функции, записывая полную про-
изводную сложной функции, имеем:
(,,(,)) (,,) (,,)
xxx
axyzxy axyz axyz z
yyz
∂∂∂
y
∂
=
+⋅
∂∂∂∂
,
2
1
()
()
(, ,(, )) (, ,(, ))
xy
yx
b
xx
Dayx
aa
x
y z x y dxdy dx x y z x y dy
yy
∂∂
−=−
∂∂
∫∫ ∫ ∫
=
=
+
22
(, ()),(, ())
b
x
a
axyx zxyxdx−
∫
11
(, ()), (, ())
b
x
a
axyx zxyxdx=
∫
=
(, ,)
x
L
axyzdx
∫
.
Докажем последнее преобразование.
(, ,)
x
L
axyzdx
∫
…
12
(, ,) (, ,)
xx
LL
axyzdx axyzdx=+
∫∫
=
xt
{пусть L задана параметрически}…
=
=
21
12
( (), (), ()) () ( (), (), ()) ()
tt
xtxt
tt
a xt yt zt xt dt a xt yt zt xt dt⋅+ ⋅
∫∫
…{
tx;() 1
t
=
=
}…=
=
.
11 2 2
(, (),( ())) (, (),( ()))
ba
xx
ab
axyxzyx dx axyxzyx dx+
∫∫
Остальные два слагаемых рассматриваются аналогично. Почленное сумми-
рование этих выражений приводит к формуле Стокса.
!
1). Используя обозначение ротора, формулу Стокса можно переписать в
векторном виде:
=
()
L
adr⋅
∫
( )rot a d
σ
Σ
⋅
∫∫
. Поток вектора через ори-
ентированную поверхность
rot a
Σ
равен циркуляции поля по контуру L,
ориентированному в соответствии с ориентацией
a
Σ
.
2). Для того чтобы криволинейный интеграл по любому кусочно-
гладкому контуру равнялся нулю, необходимо и достаточно, чтобы вы-
полнялись условия Стокса:
;
y
z
a
a
yz
∂
∂
=
∂
∂
;
x
z
aa
zx
∂
∂
=
∂
∂
y
x
a
a
x
y
∂
∂
=
∂
∂
.

Лекция 5 - 9
72
Пример:
Вычислить циркуляцию вектора
kzjxiya −+=
2
по контуру L:
22
4;
3;
xy
z
⎧
+=
⎨
=
⎩
,
2cos ;
2sin ;
3.
x
t
yt
z
=
=
=
⎧
⎪
⎨
⎪
⎩
.
Решение:
1) Вычислим циркуляцию вектора непосредственно:
2
22
0
{2 sin 2( sin ) 4 cos 2 cos 3 0}
L
C ydx x dy zdz dt t t t t
π
=
+−= ⋅−+ ⋅ −⋅
∫∫
=
= - 4
+8 =
2
2
0
sin tdt
π
∫
∫
π
2
0
2
sincos ttd
−
4
dt
t
∫
−
π
2
0
2
2cos1
+8 =
∫
−
π
2
0
2
sin)sin1( tdt
=
2
0
1
4|
2
t
π
−+
2
0
sin 2 |t
π
+
−
π
2
0
|sin8 t
π
π
4|
3
sin
8
2
0
3
−=
t
;
2) Вычислим циркуляцию вектора по теореме Стокса::
()Crotad
σ
Σ
=⋅
∫∫
=
0
()rot a n d
σ
Σ
⋅
∫∫
=
()
(0,0,1)rot a d
σ
Σ
⋅
∫∫
=
()
z
rot a d
σ
Σ
∫∫
=
(1 2)
x
d
σ
Σ
−+
∫∫
=…
2
{
ijk
rota
x
yz
yx z
∂∂∂
=
∂∂∂
−
=
00 (12)ij x++−+ k
} =
(2 1)
xy
D
x
dxdy−
∫∫
=
22 2 2 2
2
0
00 0 0 0
(2 cos 1) (2 cos 1) {2 sin | 2 }ddddd
π
π
π
ϕ
ρϕ ρρ ρρ ρϕ ϕ ρρρϕ π
=−= −= −
=
∫∫ ∫ ∫ ∫
2
2
0
2
244
22
ρπ
π
π
=
−=−⋅=−
.
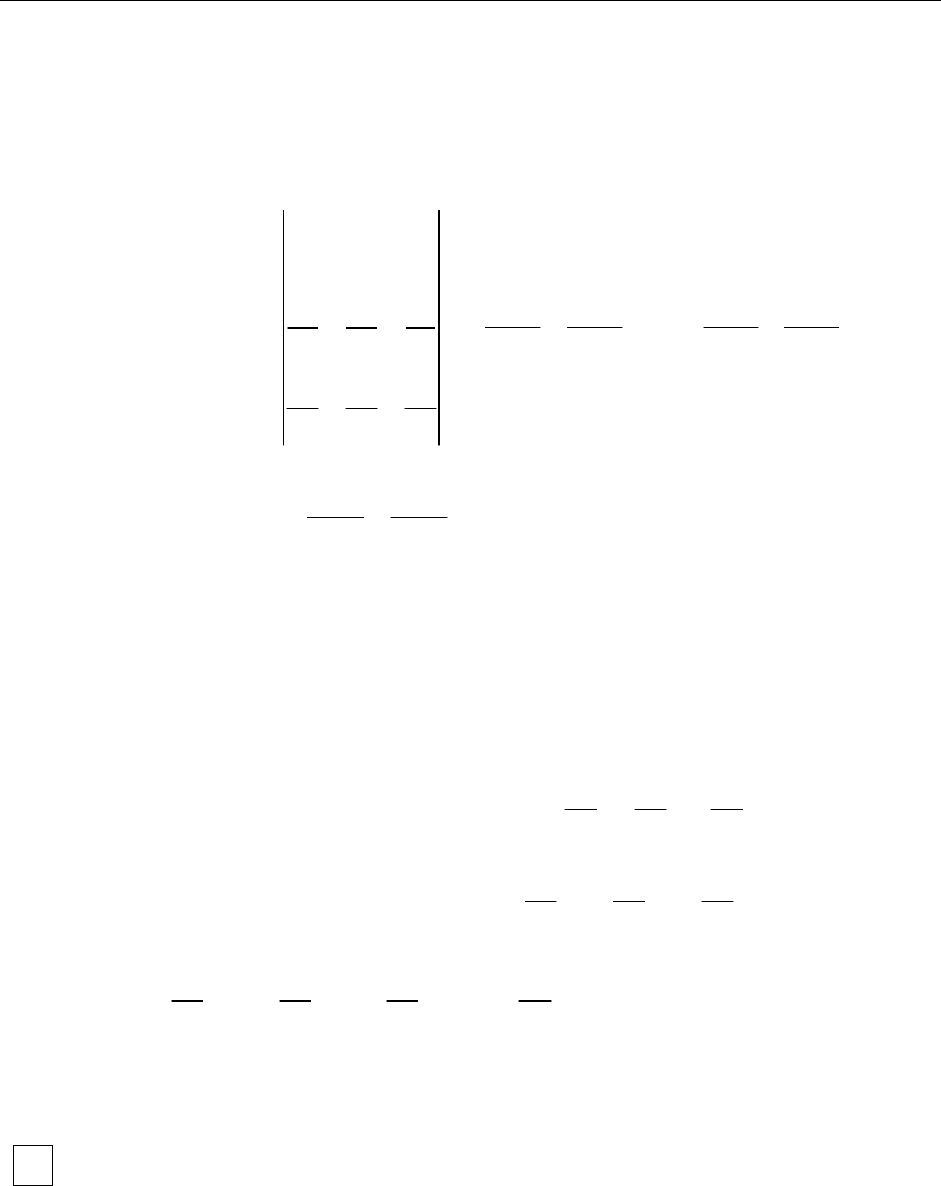
X
Z
Y
xy
8.7. Инвариантное определение ротора
Ранее было дано определение ротора
x
yz
ijk
rota
x
yz
aaa
∂
∂∂
=
∂
∂∂
, справедливое
лишь в декартовой системе координат.
Теорема Стокса позволяет дать инвариантное (независящее от системы
координат) определение ротора векторного поля.

Теория поля
73
Пусть - векторное поле, удовлетво-
ряющее теореме Стокса;
- некоторое фиксирован-
ное направление, проходящее через точку М;
D - плоская область величины
(aaP=
)
0
n
D
S
, охватывающая
точку М, а L - граница области D. Направления обхо-
да контура L и ориентация области D согласованы в
соответствии с теоремой Стокса:
a
n
o
M
()
L
adr⋅
∫
=(rot a d )
σ
Σ
⋅
∫∫
или ()rot a d
σ
Σ
⋅
∫∫
0
p
n
D
rot a d
σ
Π
∫∫
)
= .
По теореме о среднем существует точка М
1
:
0
1
p() (
nD
L
rot a M S a dr
Π
⋅= ⋅
∫
.
Тогда
0
1
()
p()
L
n
D
adr
rot a M
S
⋅
Π=
∫
. Будем стягивать контур L в точку М, тогда
точка M
1
→ M и =
0
p()
n
rota MΠ
()
lim
L
LM
D
adr
S
→
⋅
∫
. Поскольку
()
L
D
adr
S
⋅
∫
- средняя
поверхностная плотность циркуляции поля по площади S
D,
то проекция
на правление
не зависит от выбора систем координат и равна по-
верхностной плотности циркуляции вектора
()rot a
0
n
a
по контуру L, который стяги-
вает площадку, перпендикулярную этому направлению.
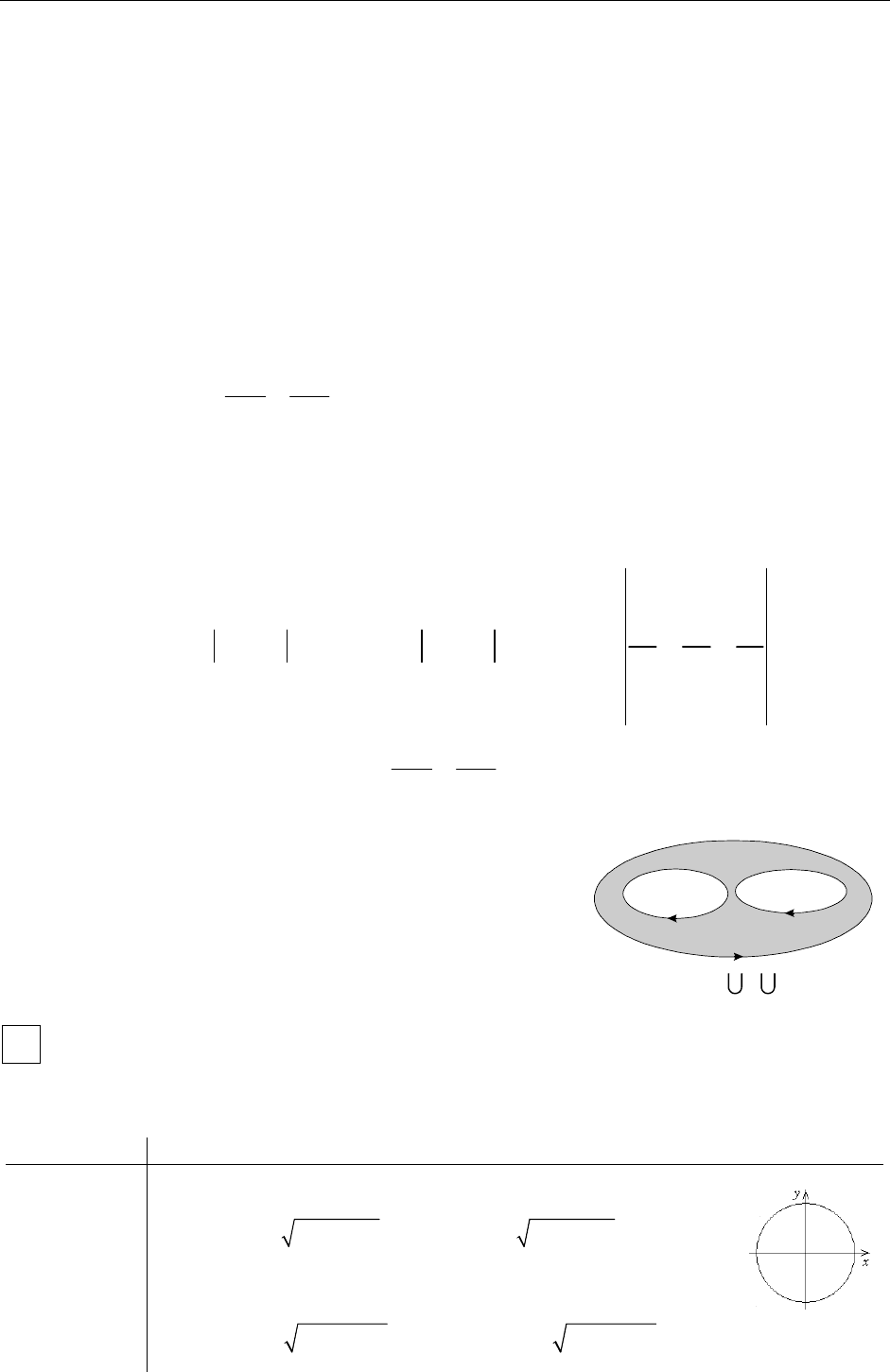
8.8. Физический смысл ротора
Пусть вектор
задает поле линейных скоростей жидкости, дви-
жущейся вокруг оси Oz, и в точке Р угловая скорость вращения
()aVP=
k
ω
ω
=
.
Тогда
() 0 0 ,
ijk
VP r yi xj
xyz
ω
ωω ω
=×= =− +
вычислим
() 0 0 ( ) 2
0
ijk
rotV P i j k k
xyz
yx
ω
ωω
ωω
∂∂∂
==⋅+⋅++
∂∂∂
−
=
.
Итак, ротор поля линейных скоростей равен удвоенной угловой скоро-
сти вращения
ω
бесконечно малого объема, окружающего точку Р, в предпо-
Лекция 5 - 9
74
ложении, что в рассматриваемый момент времени этот объем жидкости вне-
запно отвердел. Это объясняет название «вихрь» вектора, так как в обычном
представлении вихрь связан с интенсивностью вращения движущихся частиц
жидкости (турбулентность, водоворот).
8.9. Формула Грина
Пусть в односвязной плоской области D, имеющей границу , задано
непрерывно дифференцируемое векторное поле
L
x
y
aaiaj=+
, тогда
=
()
xy
L
adx ady+
∫
y
x
D
a
a
dxdy
xy
∂
⎛⎞
∂
−
⎜⎟
∂∂
⎝⎠
∫∫
, при этом контур обходится так, чтобы
область D оставалась слева.
Доказательство:
Рассмотрим формулу Стокса для данного случая: ( )
L
adr
⋅
∫
=( )rota d
σ
Σ
⋅
∫∫
.
DΣ→
:
cos( ) 1
γ
=
,
cos( )dxdy d
γ
σ
=
;
0
xy
ijk
rota
x
yz
aa
∂
∂∂
=
∂
∂∂
;
откуда следует
=
()
z
D
rota dxdy
∫∫
y
x
D
a
a
dxdy
xy
∂
⎛⎞
∂
−
⎜⎟
∂∂
⎝⎠
∫∫
.
Область D может быть и неодносвязной. В
этом случае под линейным интегралом по-
нимается сумма интегралов по всем ком-
понентам границы D.
L
1
L
3
D
L
2
123
LL L L
=
!
В некоторых случаях формула Грина позволяет упростить вычисление
циркуляции векторного поля.
Пример:
Вычислить циркуляцию вектора
22 22
1[ln(1)]axyiyxyxxyj+ + + +++=+
по контуру L: x
2
+ y
2
= R
2
.
Тогда:
(
)
22 22
1ln1
L
Cxydxyxyxxydy
⎡
⎤
=++ + ++++
⎢
⎥
⎣
⎦
∫
.

Теория поля
75
Проще вычислить циркуляцию по формуле Грина:
22
1 yx
y
y
a
x
++
=
∂
∂
,
22
22
2
1
1
1
yxx
yx
x
y
y
x
a
y
+++
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
++
+
+=
∂
∂
=
(
)
(
)
22
22
22
22 22
1
.
1
11
xyx
y
yy y
xy
xyx xy
+++
=+ =+
++
++ +++
С=
()
L
adr
⋅
∫
=
xy
y
x
D
a
a
dxdy
xy
∂
⎛⎞
∂
−
⎜⎟
∂∂
⎝⎠
∫∫
=
2
22 22
11
xy
D
yy
yd
xy xy
⎛⎞
+−
⎜⎟
⎜⎟
++ ++
⎝⎠
∫∫
xdy
R
dd
π
=
2
xy
D
ydxdy=
∫∫
=
2
22
00
(sin)
∫∫
−
π
ρρϕ
ϕ
2
00
3
2
2cos1
R
dd
ϕ
ρρρ ϕ
∫∫
= =
=
2
44
2
0
0
1sin2 1
|2
42 4 42 4
RR
π
π
4
R
ϕ
π
ϕπ
⎧⎫
⎪⎪
⎛⎞
⋅− =⋅=
⎨⎬
⎜⎟
⎝⎠
⎪⎪
⎩⎭
.
9.1. Потенциальное векторное поле
Векторное поле
называется потенциальным, если оно является гра-
диентом некоторого скалярного поля (функции)
, т.е.
. Это векторное равенство равносильно трем скалярным:
a
()uuP=
()agradu=
(, ,)
(, ,)
x
uxyz
axyz
x
∂
=
∂
;
y
u
a
О
;
z
u
a
z
∂
=
∂
y
∂
=
∂
. Иначе:
xyz
du a dx a dy a dz
=
++
.
Функция u в этом случае называется
силовой функцией, или потен-
циалом
поля.
Потенциал u определяется с точностью до постоянного слагаемого.
Пример:
Показать, что поле
r
r
e
a
3
=
потенциально.
Решение:
Рассмотрим функцию
e
u
r
=
−
;
222
z
2
11u
eexy
xxrrx
∂∂ ∂
⎛⎞
=− = + +
⎜⎟
∂∂ ∂
⎝⎠
=
2
222
12
2
x
e
r
x
yz
⎛⎞
⎜⎟=
⎜⎟
⋅++
⎝⎠
=
3
x
e
;
r
3
uy
e
yr
∂
=
∂
;
3
uz
e
zr
∂
=+ ⇒
∂
3
()
e
grad u r
r
=+
;
()agradu
=
⇒
u - потенциал
поля
.
a
!
Лекция 5 - 9
76
9.1.1. Условия потенциальности поля
1. Циркуляция векторного поля по любому замкнутому контуру, лежащему
в области непрерывности потенциального поля, равна нулю.
Доказательство:
Рассмотрим
(())rot grad u =
ijk
x
yz
uuu
x
yz
∂∂∂
=
∂∂∂
∂∂∂
∂∂∂
22
uu
i
yz zy
⎛⎞
∂∂
−
⋅
⎜⎟
∂∂ ∂∂
⎝⎠
22
uu
j
x
zzx
⎛⎞
∂∂
−−
⎜⎟
∂∂ ∂∂
⎝⎠
+
22
0
uu
k
xy yx
⎛⎞
∂∂
+−⋅=
⎜⎟
∂∂ ∂∂
⎝⎠
0.rota⇒=
По теореме Стокса
=
()
L
adr⋅
∫
( )0rota d
σ
Σ
⋅
=
∫∫
.
2. Линейный интеграл в потенциальном поле не зависит от пути интегри-
рования и равен разности потенциалов поля в конечной и начальной
точках интегрирования.
Доказательство:
Так как поле потенциально:
()agradu
=
=
uu u
ijk
x
yz
∂
∂∂
++
∂
∂∂
()
AB
adr
∪
⋅
∫
=
xyz
AB
adx ady adz
∪
++
∫
=
AB
uuu
dx dy dz
xyz
∪
⎛⎞
∂∂∂
++
⎜⎟
∂∂∂
⎝⎠
∫
=
=
() () ()
B
A
t
t
uuu
dt x t y t z t
xyz
∂∂∂
⎧⎫
++
⎨⎬
∂∂∂
⎩⎭
∫
=
B
A
t
t
du
dt
dt
∫
=
B
A
t
t
du
=
∫
((), (),())|
B
A
t
t
uxt yt zt
=
(( ), ( ),( )
BBB
uxt yt zt= ( ( ), ( ), ( )) ( ) ( )
AAA
t yt zt uB uA
-
ux
=
−
.
(Условие 3) Для того чтобы векторное поле
()aaP
=
в некоторой одно-
связной области G было потенциальным, необходимо и достаточно,
чтобы оно было безвихревым, т.е.
() 0rot a
=
.
Доказательство:
Необходимость.
Пусть
aa
- потенциальное поле
⇒=()P=
()agradu
.
(())rota rot grad u⇒= =
0
Т
Теория поля
77
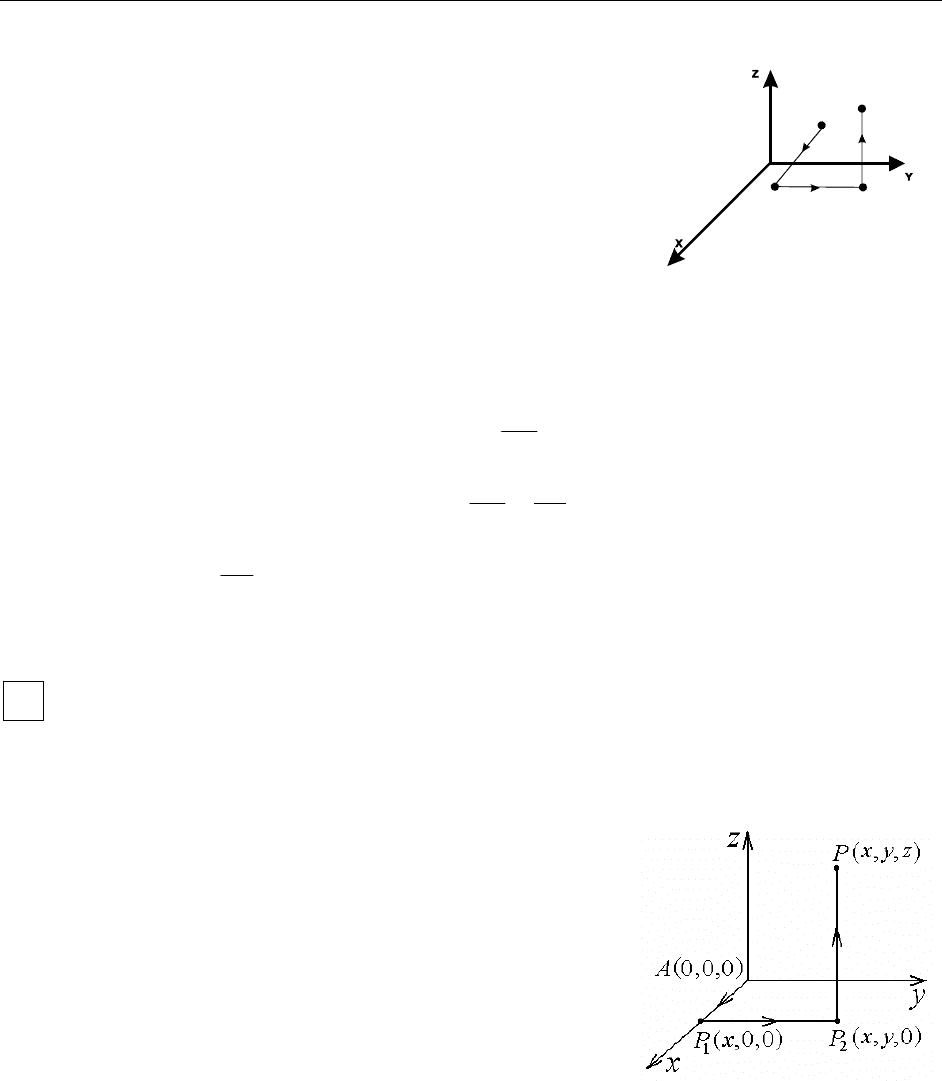
Достаточность.
В силу свойства 2,
если зафиксировать на-
чальную точку А(0,0,0), криволинейный ин-
теграл станет некоторой функцией пере-
менной точки P(x,y,z): u(P) =
()
AP
adr
∪
⋅
∫
.
Вычислим производную по направлению
функции u(P) в точке A. При переходе от
точки P к точке P' функция u получит при-
ращение
=
u∆=
'
()
PP
adr
∪
⋅
∫
'
'
PP
PP
np adl
∪
∫
'1
()
PP
np a P l
=
⋅∆
, где по
теореме о среднем. Следовательно,
1
'PPP∈
'1
()
PP
u
np a P
l
∆
=
∆
. Переходя к пределу
при
P
A→
и , имеем
0l∆→
0
lim
l
∆
→
()
AP
uu
np a A
ll
∆
∂
==
∆
∂
. Поскольку произ-
водная поля
u
l
∂
∂
по направлению AP равняется проекции grad(u) на это
направление, то
.
()agradu⇒=
A(x,y,z)
000
P1(x,y ,y )
00
P2(x,y,y )
0
P(x,y,z)
!
Условие 3 часто используют в качестве критерия потенциальности век-
торного поля.
9.1.2. Вычисление потенциала поля
Потенциал векторного поля по условию 2
может быть найден по формуле
xyz
AP
u a dx a dy a dz
∪
=++
∫
, где А (x
0
, y
0
, z
0
) - фик-
сированная точка поля, координаты которой
удовлетворяют условиям существования полей
и ( как правило, А(0,0,0)), а Р(x,y,z) - те-
кущая точка поля). Линейный интеграл вычисля-
ется по любому контуру дуги
. Наиболее
удобен для вычисления контур в виде ломаной,
звенья которой параллельны осям координат.
a
rot a
:LAP∪
В этом случае
0
00
(, ,) (, , )
x
x
x
uxyz a xy z dx=
∫
0
0
(, , )
y
y
y
axyzdy+
∫
0
(, ,)
z
z
z
axyzdy+
∫
.

Лекция 5 - 9
78
Пример:
Доказать, что поле
222
axiyjzk=++
является потенциальным,
и найти его потенциал.
Решение: Используя критерий потенциальности поля (условие 3),
имеем:
- потенциальное поле.
() 0rot a a=⇒
u =
()
AB
adr
∪
⋅
=
∫
222
AB
x
dx y dy z dz
∪
+
+=
∫
112 2
... ... ...
AP P P P P∪∪ ∪
++
∫
∫∫
1
A
P∪
:
00;0ydyzdz=⇒ = =⇒ =0;
z
y
12
PP∪
: ;
const 0; 0xdx=⇒==
2
PP∪
:
const 0;xdx=⇒= const 0yd
=
⇒=
3
33
222
00 0
3
y
xz
xyz
u x dx y dy z dz c
++
=++=
∫∫∫
+
Проверка:
333 2
3
()
33
x
yz x
grad u grad i
++
==
+
j
y
3
3
2
+
k
z
3
3
2
=
222
xi y j zk++
.
9.2. Соленоидальное поле
Векторное поле
называется соленоидальным (трубчатым), если
в каждой точке
()aaP=
P
заданного поля
() 0div a
=
.
О
9.2.1. Свойства соленоидального поля
1. Соленоидальные поля не имеют источников и стоков, что следует из оп-
ределения.
2. Поток
через любую замкнутую ориентированную кусочно–гладкую
поверхность, лежащую в поле равен нулю:
a
()
G
П ad divadV
σ
Σ
=⋅= =
∫∫ ∫∫∫
0
.
3. В соленоидальном поле векторные линии не могут начинаться или кон-
чаться во внутренней точке области; они либо замкнуты, либо начина-
ются и кончаются на границе поля.
4. Поток векторного поля через поперечное сечение векторной трубки в
соленоидальном поле остаётся постоянным вдоль всей трубки.

Теория поля
79
Доказательство свойства 4:
Рассмотрим область специального вида
- векторную трубку Т ограниченную двумя
поперечными сечениями Σ
1
, Σ
2
и боковой
поверхностью Σ
3
.
3
1
2
+
2
−
a
a
0
n
0
n
Вычислим поток через указанную поверх-
ность.
12
ΠΠ Π
ΣΣ
=
3
Π
Σ
++=
0
T
diva dV
=
∫∫∫
a
0
n
(по свойству 2);
3
Π
Σ
=
Π
боковой
поверхности
3
()ad
σ
Σ
=⋅
∫∫
=
3
0
()an d
σ
Σ
0
⋅
=
∫
∫
, так как на поверх-
ности векторной трубки Σ
3
вектор
a
направлен по касательной к по-
верхности, т.е.
3
0
()an
Σ
⊥
3
0
()an
Σ
0=⇒⋅
.
Таким образом,
12
0
ΠΠ
ΣΣ
+=
, ,
⇒
12
ΠΠ
ΣΣ
=−
1
()ad
σ
Σ
⋅
∫
∫
=
2
()ad
σ
Σ+
−⋅
∫
∫
=
2
()ad
σ
Σ−
⋅
∫∫
.
Если придать векторному полю смысл скорости течения жидкости, то
количество жидкости, вытекающей из поперечного сечения векторной
трубки, всегда равняется количеству жидкости, втекающей в нее.
Пример:
1). Является ли соленоидальным поле:
222 2
()(3ayi x yjzy k=−+ + +1)
?
Решение:
2
23 10diva y y=− + + ≠
a
⇒
- не соленоидально.
2). При каком условии векторное поле
()arr
ϕ
=
⋅
будет соленоидаль-
ным?
Решение:
[()] () ( () ) 3() ()
r
diva div r r r divr grad r r r r r
r
ϕϕ ϕ ϕϕ
⎛⎞
′
==+⋅=+⋅
⎜⎟
⎝⎠
=
2
()
3() 3() ()
r
rrr
r
rr
ϕ
ϕϕ
′
′
+=+
ϕ
или
3() ()rrr
ϕ
ϕ
′
=−
,
rr() 3 ()r
ϕ
ϕ
′
=
−
,
3
dd
r
r
ϕ
ϕ
=−
,
ln ln 3lncr
ϕ
=−
;
3
c
r
ϕ
=
- поле соленоидально, если
3
c
r
ϕ
=
.
Лекция 5 - 9
80
9.3. Операторы Гамильтона и Лапласа
9.3.1. Оператор Гамильтона (набла)
Многие операции векторного анализа могут быть записаны в сокращен-
ной и удобной для расчётов форме с помощью символического оператора
Гамильтона «набла»:
;;ijk
x
yzxyz
⎧
∂∂∂∂∂∂
⎫
∇= + + =
⎨
⎬
∂∂∂∂∂∂
⎭
⎩
.
Выражение вида
понимается как результат действия операто-
ра на соответствующую функцию. Тогда
(, ,)uxyz∇
(, ,) (, ,)uxyz i j k uxyz
xyz
⎛⎞
∂∂∂
∇=++⋅ =
⎜⎟
∂∂∂
⎝⎠
uu u
ijk
x
yz
∂
∂∂
++
∂
∂∂
xy z
ui u j uk
′
′′
++
,
g
radu u
=
∇
. =
В этом операторе соединены дифференциальные и векторные свойства,
поэтому при действиях с ним необходимо пользоваться правилами векторной
алгебры и дифференцирования.
Выполняя действия с оператором «набла», удобно использовать так на-
зываемый
символический метод, основанный на применении следующих
правил:
1. Если оператор
действует на какое-либо произведение, то вначале ис-
пользуются его дифференциальные, а затем векторные свойства.
∇
2. Чтобы отметить тот факт, что «набла» не воздействует на какую-либо
величину, входящую в состав сложной формулы, эту величину помеча-
ют индексом c (const).
3. Все величины, на которые оператор «набла» не действует, в окончатель-
ном
варианте ставятся впереди него.
Пример:
Используя символический метод, вычислить
div a b
⎡
⎤
×
⎣
⎦
.
Решение:
Воспользуемся свойствами смешанного произведения:
()
div a b a b
⎡⎤ ⎡⎤
×
=∇⋅ × =
⎣⎦ ⎣⎦
(
)
(
)
cc
ab a b
⎡
⎤⎡⎤
∇
⋅× +∇⋅ × =
⎣
⎦⎣⎦
(
)
()
baab
⎡⎤
⎡⎤
⋅∇× − ⋅∇× =
⎣⎦
⎣⎦
=
.
() ()brota arotb⋅−⋅
