Stacey F.D., Davis P.M. Physics of the Earth

Подождите немного. Документ загружается.

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C16.3D

–

247

– [239–266] 13.3.2008 11:41AM

lower crust, and possibly the uppermost mantle,

trap energy from large surface explosions that

travels as apparent P

waves, refracted head

waves (Section 17.2), at the crust–mantle boun-

dary (Moho) to much greater distances than

expected if the P

were head waves generated

beneath homogeneous crust overlying homoge-

neous mantle (Morozov and Smithson, 2000).

This discussion illustrates the importance of

knowing the distribution of scatterers in the

mantle when comparing Earth models derived

from seismic waves of different frequencies.

Roth et al. (1993) used finite difference calcula-

tions to examine travel time variations in a

medium permeated with scatterers with higher

than average velocity, and found that at high

frequencies the wavefront is dominated by wave-

lets that have taken the fast paths through the

high-velocity material. Thus, the travel time is

shorter at high frequencies than that at low fre-

quencies for which the waves respond to an aver-

age modulus of the medium. In Section 17.8 this

phenomenon is mentioned as a possible reason

for the discrepancy between models derived from

body waves and normal modes.

16.4 Reflection and transmission

coefficients at a plane

boundary

The directions of waves refracted and reflected

as plane waves are given by Snell’s law

(Eq. (16.6)). We are interested also in the relative

amplitudes of reflected and refracted waves, the

analysis of which gives some insight into the

behaviour of guided waves. These include sur-

face waves (Section 16.5) and also head waves

that are the subject of Section 17.2. As we

show, reflection and refraction amplitudes are

controlled by the parameter known as acoustic

impedance, which, for each medium and wave

type, is the product of density and wave speed,

V

or V

. Thus, observations of reflected waves

give information about the contrasts in density

and elasticity at boundaries. Observations of

waves with different wavelengths may also

show whether a boundary is sharp or marks

a gradual transition in properties, because reflec-

tions occur only at boundaries that are sharp

in the sense of having thickness much less

than the wavelengths of waves used to observe

them.

Consider a P-wave u

¼ A

exp½iðk

z  !t Þ,

normally incident on a plane boundary at z ¼0,

separating materials of contrasting density and

P-wave velocity given by, 

; V

and 

; V

(Fig. 16.4(a)) (the subscript i here indicates the

incident wave and is not to be confused with

i ¼

ﬃﬃﬃﬃﬃﬃﬃ

1

in the exponential factor). Let the trans-

mitted wave be u

¼ A

exp½iðk

z  !tÞ and the

reflected wave u

¼ A

exp½iðk

z  !tÞ. Conti-

nuity of displacement requires

þ A

¼ A

: (16:17)

Normal stress is given by



¼ 

¼ ikAe

iðkz!tÞ

: (16:18)

Continuity of normal stress requires that



þ 

¼ 

;



 k



¼ k



(16:19)

Let the reflection coefficient be R, transmission

coefficient T and A

¼ A:

From (16.17),

A þ RA ¼ TA or 1 þ R ¼ T; (16: 20)

and from (16.19),



 k

R

¼ k

T

: (16:21)

With V

ﬃﬃﬃﬃﬃﬃﬃﬃ

=

; and k ¼ !=V

; Eq. (16.21) becomes



 

R ¼ 

FI G U R E 16.4 (a) Reflected and transmitted phases at

normal incidence to an interface. (b) Reflected phases from

a free surface at inclined incidence.

16.4 REFLECTION AND REFRACTION 247

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C16.3D

–

248

– [239–266] 13.3.2008 11:41AM

Combined with Eq. (16.20), this gives

R ¼



 



þ 

; (16:22)

T ¼

2



þ 

: (16:23)

These expressions illustrate the significance of

acoustic impedance, V

At a free surface Eq. (16.22) gives R ¼ 1,

¼ A

, so the reflected wave and the incident

wave constructively interfere and the amplitude

is doubled. Because the reflected wave adds con-

structively to the incident wave, the doubling of

a pulse occurs over a depth range equal to half

the dimension of the pulse. The stress at a free

surface must be zero at all times. Note that the

reflected wave is u

¼ A exp½ iðk

z  !tÞ. So the

stress is 

¼k



A exp ½iðk

z  !tÞ, whereas

the incident wave had a stress given by



¼ k



A exp½iðk

x  !tÞ. The reflected and

incident waves have opposite stresses, while

the displacements are additive. At the surface,

an incident tension is cancelled out by a reflected

compression that travels downwards. The dis-

placements have the same polarity relative to

the z-axis, but relative to the direction of propa-

gation, which for the reflected wave is the nega-

tive z-direction, the displacement is negative.

Phase reversals of reflected waves occur when-

ever the impedance of the second medium is less

than that of the first. Examples of 180



phase

reversals include P-waves reflected from low

velocity zones such as the core–mantle boun-

dary, or the surface of the Earth.

At an interface with a medium of infinite

acoustic impedance the amplitude would

become zero. Then by Eq. (16.17) A

¼A

, that

is the reflected and incident waves cancel at the

surface, which is a node of a standing wave in the

softer medium. Note that sometimes reflection

and transmission coefficients are given for

potentials instead of amplitudes, and we now

use this convention.

Up to this point we have dealt with solutions

to the one-dimensional wave equation in the

form exp½iðkz  !tÞ. In considering reflection

and refraction at boundaries that are not parallel

to the wavefronts (Fig. 16.4(b)), the analysis of

seismic displacements

u is simplified by decom-

posing it into gradients of (Helmholtz) potentials

that allow P- and S-wave motions to be treated

separately (e.g., Aki and Richards, 2002). The

P-wave and S-wave components of

u are

expressed as

u ¼r þrw; (16:24)

where the potentials  and w satisfy P- and

S-wave equations

€

 ¼ V

; (16:25)

€

w ¼ V

w: (16:26)

In the two-dimensional case the P-wave equation

becomes

€

 ¼ V





: (16:27)

A solution to this equation is

 ¼ exp½iðk

x þ k

z  !tÞ: (16:28)

Now we consider the problem of a wave travel-

ling parallel to a boundary in the x-direction but

with amplitude decaying in the z-direction. This

corresponds to k

being imaginary.

Let k

¼ i!

 ¼ expð!

zÞexp½iðk

x  !tÞ: (16:29)

After differentiation and substitution in

Eq. (16.27),

¼ 

; (16:30)

where V

is the velocity in the x-direction.

We see that V

and depends on the value

of 

. Similarly for the S-wave potential, w ¼

expð!

zÞexp½iðk

x  !tÞ and

¼ 

: (16:31)

Equations (16.30) and (16.31) describe inhomo-

geneous (P and S) waves that propagate in the

x-direction and diminish with depth in the

z-direction. Consider a situation in which

P-and S-waves have horizontal velocities equal

¼ V

). Then by Eqs. (16.30) and (16.31) the

depth dependences of the compressional and

248 SEISMIC WAVE PROPAGATION

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C16.3D

–

249

– [239–266] 13.3.2008 11:41AM

shear components are different (

6¼ 

). Such

waves, travelling along a free surface with ampli-

tudes that satisfy the free surface boundary

condition, are Rayleigh waves (Section 16.5)

with wave velocity c

¼ V

, which, by

Eq. (16.31), must be less than V

because 

is real.

At a surface or interface, the boundary con-

ditions must be satisfied by matching the total

stresses and displacements of all homogeneous

and inhomogeneous waves. Because the  are

squared they can be either positive or negative

and still satisfy the wave equation. Such inter-

face waves decrease or increase exponentially on

either side of a boundary, but generally the

increasing solution is discarded to avoid the

unphysical situation of unbounded energy at

infinity. Stoneley (1924) waves are P-SV waves

(like Rayleigh waves) but at the interface of two

half spaces (as discussed in detail by Aki and

Richards, 2002, p. 156).

We now consider the case of a non-normal

incident SV-wave at an angle i

to a free surface

(Fig. 16.2), at which there is no transmission.

It will generate both a P-wave reflection at

angle r

and an S-wave reflection at angle i

,as

given by Snell’s law (Eq. (16.6)), represented by

the plane layer ray parameter p ¼

sin r

sin i

(In the present discussion we are not con-

cerned with spherical Earth geometry and it

is convenient to use this version of the ray

parameter, which we refer to as the plane

layer ray parameter, to distinguish it from the

parameter used with spherical Earth geo-

metry and defined by Eq. (17.13).) In this case

¼ !

sin r

¼ !p ; k

¼ 0; k

¼!

cos r

¼!,

where p and  are the horizontal and vertical

slownesses (inverse speeds) for the P-waves and

we set  ¼ cos i

to be the vertical slowness of

the S-waves. In summary,

p ¼

sin r

sin i

; (16:32)

 ¼

cos r

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1=V

 p

; (16:33)

 ¼

cos i

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1=V

 p

: (16:34)

Consider an incident S wave of unit amplitude

given by

¼½u

; u

¼½cos i

; sin i

exp i!ðpx  z  tÞ½:

(16:35)

The reflected P-wave is

¼½u

; u



¼ R

½sin r

; cos r

exp i!ðpx þ z  tÞ½;

(16:36)

and the reflected S-wave is

¼½u

; u



¼ R

½cos i

; sin i

exp i!ðpx þ z  t½;

(16:37)

where R

and R

are the amplitudes of the

reflected P- and S-waves relative to the incident

S-wave. R

and R

must satisfy the condition of

zero traction on the free surface. We apply

Eqs. (11.15) and (11.19) for the tractions, which

are set to zero,

2pV

R

þð1  2V

Þð1  R

Þ¼0;

ð1  2V

ÞR

þ 2V

p=V

ð1 þ R

Þ¼0;

(16:38)

yielding solutions

4pV

1=V

 2p



RðpÞ

; (16:39)

1=V

 2p



4p



RðpÞ

; (16:40)

where the common denominator is known as

the Rayleigh function,

RðpÞ¼ 1=V

 2p



þ 4p

: (16:41)

For the case of an incident P-wave, following

the same procedure, it can be verified that

¼R

and R

¼R

ðV

Þ=ðV

Þ. These coef-

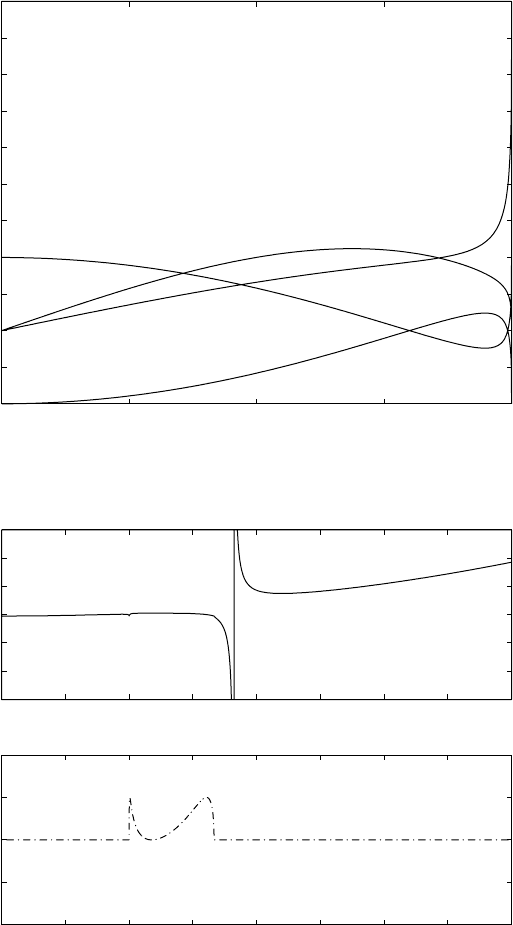
ficients are plotted in Figure 16.5(a). The

reflected and transmitted waves show consider-

able variations in amplitude as functions of inci-

dence angle. When 1=V

> p > 1=V

the reflected

P-waves are inhomogeneous and the reflected

S-wave is homogeneous (see Eqs. (16.33) and

(16.34)). For an incident homogeneous P-wave

16.4 REFLECTION AND REFRACTION 249

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C16.3D

–

250

– [239–266] 13.3.2008 11:41AM

p cannot exceed 1=V

.Ifp

1=V

the

interpretation is different. All waves along

the interface, both incident and reflected, are

inhomogeneous and R

, R

and p are related by

Eq. (16.39) and Eq. (16.40) with complex angles since

sin r

¼ pV

1and sini

¼ pV

1. Real and

imaginary coefficients of R

are plotted in

Fig. 16.5(b) for a range of p that includes

inhomogeneous waves. Although we have con-

sidered a free surface, the analysis can be gener-

alized to a boundary between contrasting media,

with similar results. In general, at non-normal

0 0.05 0.1 0.15 0.2

−1

−0.5

0.5

1.5

2.5

3.5

4.5

Free surface P−SV reflection coefficients

FI G U R E 16.5(a) Homogeneous

reflection coefficients for P-waves

, R

, and incident S-waves R

, R

from a free surface as a function of

the plane layer ray parameter, p, with

¼ 5km=s and V

¼ 3km=s.

−60

−40

−20

Free surface PP reflection coefficients

Real R

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8

−2

−1

Imag R

FI G U R E 16.5(b) Real (solid curve)

and imaginary (dotted) R

reflection

coefficients as a function of the plane

layer ray parameter, p (Eq. (16.32)),

including the inhomogeneous range

at p > 0.2, for the velocities assumed

(as for Fig. 16.5(a)). The coefficient

becomes singular at the Rayleigh

pole, because R(p) (Eq. (16.41))

vanishes. This value of p corresponds

to the reciprocal of the Rayleigh wave

speed, c

, but gives a value slightly

slower than observed because a very

low value of V

is assumed. The

positive and negative infinities of R

at the Rayleigh pole are unphysical,

but when the reflected P and S waves

from a spherical source (obtained

from R

and R

) are integrated (as in

Eq. (16.48)) the result gives finite

amplitude Rayleigh waves along the

surface (Aki and Richards, 2002).

250 SEISMIC WAVE PROPAGATION

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C16.3D

–

251

– [239–266] 13.3.2008 11:41AM

incidence an incident P- or S-wave generates

four waves comprised of reflected and transmit-

ted P- and S-waves. The four coefficients are

referred to as the scattering matrix for the

interface.

16.5 Surface waves

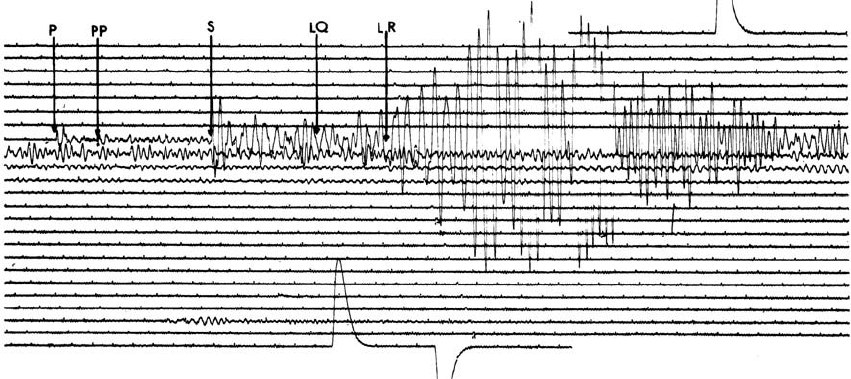
On seismic records of distant earthquakes (tele-

seisms), the waves of greatest amplitudes are

generally surface waves that have followed the

Earth’s surface and not penetrated the interior.

The exceptions are seismograms of deep focus

earthquakes, which are not effective generators

of surface waves, so that the body waves are

more prominent. The dominance of surface

waves on teleseismic records is due to the geo-

metrical effect of wave spreading. Body waves

spread out on wavefronts that are essentially

spherical. Thus, the wave energy passing

through any element of area diminishes as 1/r

where r is the distance of travel from the focus.

On the other hand, surface waves spread as an

expanding circle across the surface. Thus, at near

points the energy per unit length of wavefront

falls off only as 1/r, where r is now the radius of

the circle. Moreover, this radius does not

increase indefinitely but reaches a maximum

when the waves have travelled 908 and beyond

that it decreases again.

Body waves are almost non-dispersive and

since wave energy density is proportional to

the square of wave amplitude, body wave ampli-

tudes diminish as 1/r. The spreading of surface

wave energy does not translate as directly into

wave amplitudes, because surface waves are

strongly dispersive. The waveform changes,

becoming spread out in time, or equivalently,

distance in the direction of travel. But, in spite

of the dispersion, surface wave amplitudes

decrease less with distance than do body wave

amplitudes. In this circumstance it is convenient

that body waves are faster than surface waves

and so are not obscured by them on seismic

records (Fig. 16.6).

There are two principal kinds of surface

wave, both named after the originators of the

theories describing them. Rayleigh waves appear

as SV-waves, with a coupled P-wave component,

as considered in Section 16.4, and Love waves

propagate in the manner of SH-waves. In both

FI G U R E 16.6 Seismogram obtained at Charters Towers, Queensland (station CTA), showing arrivals of P, PP, S and

surface waves, LQ (Love) and LR (Rayleigh), from a magnitude 5.9 earthquake off northern Sumatra (D ¼548.9) on

August 21, 1967. The successive lines are parts of a continuous helical trace and this figure shows about two thirds of

the record that was unwrapped from the recording drum. There is one line per hour, with minute marks along the

traces and calibration pulses at the beginning and end of the record. This recording is from a long-period east–west

instrument, upwards on the record indicating eastward movement of the ground. The maximum amplitude of

ground motion is about 200 mm.

16.5 SURFACE WAVES 251

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C16.3D

–

252

– [239–266] 13.3.2008 11:41AM

cases the amplitudes of particle motion decrease

away from the boundaries that guide the waves,

becoming very small at depths greater than a

wavelength. The propagation of surface waves

has some similarity to the phenomenon of

wave diffraction. The necessity for their exis-

tence is less intuitively obvious than is the exis-

tence of body waves, but there are analogies that

help to give a feel for their behaviour.

Rayleigh waves resemble ocean waves. The

material particles move in vertical ellipses

which, at the surface, are retrograde, that is the

direction of motion is that of a wheel rolling

backwards relative to the progress of the wave.

The restoring force is provided by the elasticity

of the medium, and not by gravity as in ocean

waves. Another difference is that the particle

motion at depth is more complicated: the sense

of the elliptical motion is prograde in the deeper

parts, even for the fundamental mode, and there

are higher modes with nodes in the motion. But,

like open ocean waves, Rayleigh waves can pro-

pagate at the boundary of a uniform medium, or

half space, no layered structure being required.

The Rayleigh wave speed, c

, in a uniform half

space is a slight function of its Poisson’s ratio, ,

but for all reasonable values of , c

 0:92V

for

the fundamental mode (see below, Eq. (16.45)),

that is slightly less than the shear wave speed,

. In this simple case the waves are non-dispersive;

longer wavelengths penetrate deeper but are

simply scaled-up in size, and the ratio of restor-

ing force to particle displacement, which deter-

mines the wave speed, is independent of scale. In

a layered medium, such as the Earth, in which

; V

increase with depth, longer wavelengths

sample more of the higher-velocity material and

in this circumstance Rayleigh waves are disper-

sive, the phase speeds of longer wavelengths

being faster. It follows that observations of the

dispersion give an indication of the velocity

layering.

Analogies for Love waves are electrical waves

in a wave-guide or light in a light pipe or optical

fibre. They do not propagate on the boundary of

a simple half space but require velocity layering

with increasing shear wave speed, V

, at depth.

The simplest case is a uniform layer overlying a

half space, which is also uniform, but with a

higher value of V

. Love waves behave like SH-

waves that are made to follow the upper layer by

repeated reflections, the angle of incidence to

the boundary with the deeper material being

greater than the critical angle for total internal

reflection. Of course, since the two media are in

welded contact, the motion at points along their

common boundary is the same for particles on

both sides of it. Thus, a Love wave propagates in

both media, but the particle motion diminishes

exponentially with depth in the lower one as an

inhomogeneous wave. The penetration of the

lower medium increases with wavelength, so

the fraction of the wave energy propagating in

the lower one increases with the ratio of wave-

length to the thickness of the upper layer. Thus,

Love waves are necessarily dispersive, with

speeds, c

, between those of shear waves in the

two media. For the shortest wavelengths c

close to V

of the upper medium and for the

longest wavelengths it approaches the value of

in the lower one.

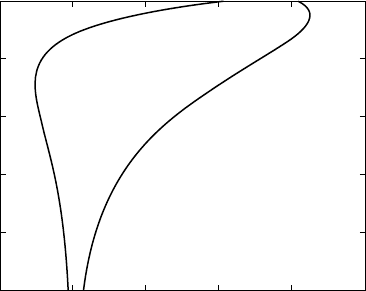
The eigenfunctions (solutions to the wave

equation) for Rayleigh waves describe their

disturbances in the vertical and horizontal

directions as functions of depth (Fig. 16.7). They

are combinations of exponential functions

that decay with depth for both P and S motions.

–2

–4

–6

–8

–10

Depth

0–0.2 0.40.2

0.6 0.8

Displacement

Rayleigh displacements

FI G U R E 16.7 Horizontal and vertical displacement

eigenfunctions for a fundamental mode Rayleigh wave

as functions of depth below the free surface of a half

space (normalized such that A sin i

¼ 1m in Eq. (16.42)).

252 SEISMIC WAVE PROPAGATION

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C16.3D

–

253

– [239–266] 13.3.2008 11:41AM

Many of the properties of Rayleigh waves can

be deduced from elementary considerations

(Knopoff, 2001) involving the stress-free boun-

dary. The mathematical theory of surface wave

propagation may be found in seismology texts,

for example Aki and Richards (2002) and Bullen

and Bolt (1985). Analytical treatments are tract-

able only in simple cases and, for the more com-

plicated situation of the Earth, numerical

methods are needed. The usual procedure is to

adjust a model of the crust and upper mantle

until it gives dispersion, the variation of wave

speed with frequency, matching what is

observed for a particular wave path. The wave

speeds are sensitive to structure to depths

of about a third of a wavelength. For Rayleigh

waves we consider inhomogeneous P- and

S-waves with the form of Eqs. (16.35) and (16.36)

where  and  are imaginary (positive) and intro-

duce amplitudes A and B for the P and S waves.

The displacements are the real components of

¼fu

; u

g¼A½sin i

; cos i

exp i!ðpx þ z  tÞ½;

¼fu

; u

g¼B½cos i

; sin i

exp i!ðpx þ z  t½;

(16:42)

where the angles are imaginary. The stresses on

the surface are equated to zero,

2pV

A þð1  2V

ÞB ¼ 0;

ð1  2V

ÞA  2V

p=V

B ¼ 0:

(16:43)

In order that these homogeneous equations have

a solution for A and B their determinant must

equal zero,

2pV

 ð1  2V

ð1  2V

Þ2V

p=V



¼ 0 ¼ð1  2V

þ 4V

 ¼ RðpÞ:

(16:44)

This is the Rayleigh function that arose in

Eqs. (16.39), (16.40) and (16.41). After rearranging

terms, Eq. (16.44) becomes a cubic equation in c

 8

þ c





 16 1 



¼ 0:

(16:45)

For a Poisson solid ðl ¼ ;  ¼ 1=4Þ the relevant

real root of this equation is c

¼ 0:92V

. The

Rayleigh wave is 8% slower than the S-wave. We

can substitute back into Eqs. (16.42) and (16.43)

to obtain the total normalized (by A sin i

ApV

¼ 1 m) horizontal and vertical displace-

ments as functions of depth. Then the Rayleigh

wave P and S components are given by

¼ expð0:85kzÞ0:58 expð0:39kzÞ

 sin½kðx  c

tÞ;

¼0:85 expð0:85kzÞ

þ1:47 expð0:39kzÞg

 cos½kðx  c

tÞ;

(16:46)

where k ¼ !=c

. These eigenfunctions are plot-

ted in Fig. 16.7.

Rayleigh waves are generated if a point

source, or distribution of point sources, is sud-

denly applied to an elastic half space. If the

source is at depth the Rayleigh waves do not

build up until the disturbance has travelled a

distance such that the wavefront makes a suffi-

cient angle with the surface to generate S. The

deeper is the source the weaker is the disturb-

ance by the time it reaches the surface; deep

earthquakes are not effective generators of sur-

face waves. A classical analysis in theoretical

seismology is the response of an elastic half

space to a point or line source, known as

Lamb’s problem (Lamb, 1904) with its extension

to a buried source (Lapwood, 1949). Three main

pulses are generated corresponding to the P, S

and Rayleigh pulses. The mathematics is compli-

cated, but exact solutions can be obtained using a

method of inverting the integral transforms

developed by Cagniard (1939, 1962) and DeHoop

(1960), known as the ‘Cagniard–DeHoop’ method.

A buried source generates P- and S-waves that

convert and reflect at the free surface, subject to

the zero traction boundary condition. Thus, as

well as the incident waves, there are four

reflected waves, giving six terms in the solution.

Consider a spherical P-wave, for example

from an underground explosion, which is inci-

dent on a free surface. Let the source be buried at

depth h below the free surface and a receiver a

distance r away at depth z. At large distances a

spherical wavefront approximates a plane wave

governed by Snell’s law, with p ¼ sin i

=V.At

small distances, where the curvature of the

16.5 SURFACE WAVES 253

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C16.3D

–

254

– [239–266] 13.3.2008 11:41AM

wavefront is appreciable, it can be decomposed

into a complex integral over the plane layer ray

parameter p (Eq. (16.32)) of homogeneous and

inhomogeneous plane waves (Aki and Richards,

2002).

Pð!Þ/

1

ﬃﬃﬃ



exp½i!ðpr þ zÞdp: (16:47)

For p

> 1=V

;is imaginary and so by Eq. (16.33)

this range in the integral corresponds to the

inhomogeneous waves. The advantage of decom-

posing a spherical wave into plane waves is that

the plane wave reflection and refraction coeffi-

cients can be used to model the effects of an

interface on a spherical wavefront. In this case

the reflected P- and S-waves are found by multi-

plying the integrand of Eq. (16.47) by R

and R

(see the argument following Eq. (16.41)). For

example, the reflected P-wave is given by

refl

ð!Þ/

1

ﬃﬃﬃ



exp½i!ðpr þ z þ hÞdp

(16:48)

(Aki and Richards 2002, Eq. 6.33). The integrand

(16.48) becomes singular at values of p for which

the denominator of R

, that is RðpÞ, becomes

zero (Fig. 16.5(b)). This is known as the Rayleigh

pole and, as we saw in Eqs. (16.44) and (16.45), is

satisfied by a value of p ¼ p

¼ 1=c

slightly

greater than 1=V

(1/0:92V

for a Poisson solid).

The integral over p is equivalent to integrat-

ing plane (homogeneous and inhomogeneous)

waves over all take-off angles from the source,

weighted by R

. It can be solved numerically or

approximately by the method of steepest

descents (Aki and Richards, 2002) or, for a delta

function source, by the Cagniard–DeHoop

method. The integrand peaks for waves with a

take-off angle given by Snell’s law, p

¼ sin i

(the saddle) and decreases exponentially (as

a Gaussian) on either side. Another peak in

the integrand occurs at the Rayleigh pole. For

small angles of incidence, p

, we obtain the

ray theory result because the exponential decay

on either side of the saddle eliminates the

contribution of the Rayleigh pole. However, as

the incidence angle increases, p

approaches

, and the contribution from the Rayleigh

pole becomes more significant than the expo-

nential decay. This occurs at an angle of inci-

dence of about 808. The reflected wave then

contains, in addition to the reflected homo-

geneous wave, an inhomogeneous P wave,

which is the P-wave component of the Rayleigh

wave. A similar integral using R

has an identi-

cal pole, and generates the S-wave component of

Rayleigh waves. We see that the coupled inho-

mogeneous P- and S-waves making up Rayleigh

waves are generated by spherical waves interact-

ing with a free surface. Above a buried source

they build up beyond a distance about six times

the depth.

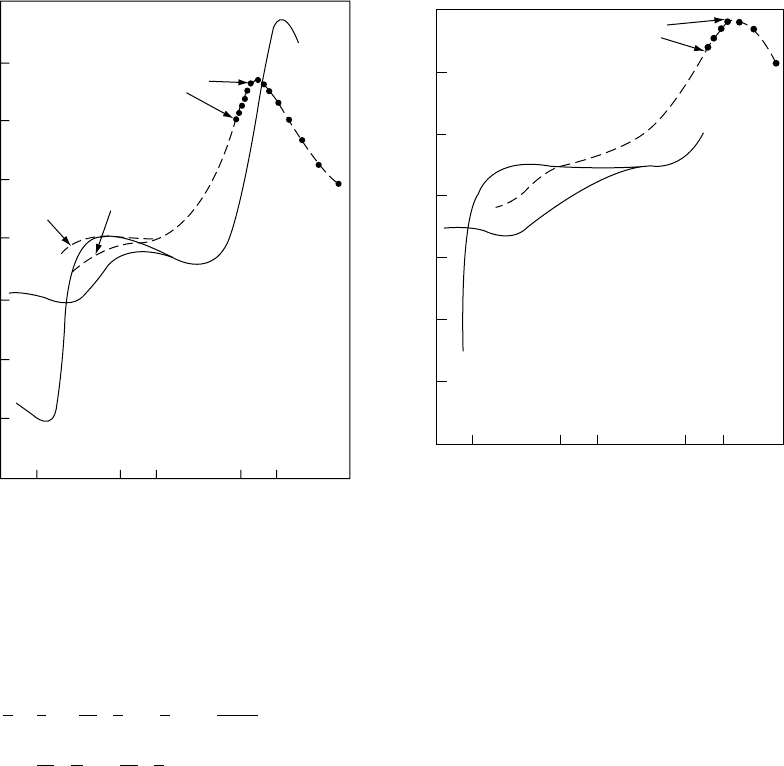
In considering the dispersion of surface

waves, it is essential to know whether it is the

phase or group speeds of the waves that are

observed. Normally, group speed, u, the speed

of the envelope of a wave packet and therefore

of wave energy, is observed, but in some cases it

is possible to identify the speed v of a particular

phase or feature of a wave. The relationship

between group and phase speeds for a wave of

wavelength l and wave-number k ¼ 2p=l is

u ¼ v þ k

¼ v  l

d l

¼l

d l

: (16:49)

In terms of frequency, f,

u ¼ v 1 



(16:50)

FI G U R E 16.8 Phase and group speeds of a wave. The

wave is represented by the solid line, with features

travelling at the phase speed, v. The amplitude or

envelope is outlined by the broken line which travels at

the group speed, u. In physical situations such as the

propagation of Rayleigh and Love waves, u < v,so

that, as the individual waves or features pass through

the envelope, they grow at the tail end and disappear

out of the head or advancing front of the envelope. The

energy of the wave travels at the group speed, u.

254 SEISMIC WAVE PROPAGATION

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C16.3D

–

255

– [239–266] 13.3.2008 11:41AM

þ f



1 

dlnv

dlnf



(16:51)

The theory of surface wave propagation in media

of specified elasticities and layer thicknesses

gives the phase speed v from which u must be

calculated by one of these equations. Over most

of the range, dv/dl is positive for both Rayleigh

and Love waves in the Earth, so by Eq. (16.49)

u < v. This means that, as represented in Fig. 16.8,

waves advance through the envelope represent-

ing their amplitude.

There are minima in the group velocity

curves for both Rayleigh and Love waves, usually

more noticeable for Rayleigh waves (Fig. 16.9).

Thus, the last arriving waves of a wave train may

be observed as a nearly sinusoidal wave of period

corresponding to the velocity minimum. It has

been called the Airy phase.

Excellent seismic records are required for the

determination of surface wave dispersion. They

must be spectrally analysed to find the speeds of

individual frequency components of complex

waveforms. At the longer periods, information

derived from surface waves merges with that

obtained from the periods of higher modes of

free oscillation.

16.6 Free oscillations

The analysis of surface waves in terms of a flat

Earth model is adequate at short periods, but

becomes progressively less satisfactory at longer

periods. Curvature of the Earth influences the

dispersion and must be taken into account. A

more general approach is to consider the

modes of free oscillation. After a large earth-

quake the Earth resonates at numerous discrete

mode frequencies, each of which may be

thought of as a standing wave resulting from

SPHEROIDAL

MODES

VELOCITY (km s

–1

)

CONTINENTAL

u (CONTINENTAL)

u (OCEANIC)

OCEANIC

WAVE PERIOD (s)

50 100 500 1000 4000

FI G U R E 16.9(a) Fundamental mode Rayleigh wave

dispersion. Group velocity, u, is shown by a solid line

and inferred phase velocity, v, by a broken line, with the

dispersion curve from free oscillation periods above

400 s. Figure based on Oliver (1962).

VELOCITY (kms

–1

)

5 10 50 100 500 1000 3000

WAVE PERIOD (s)

TOROIDAL

MODES

u (OCEANIC)

u (CONTINENTAL)

FI G U R E 16.9(b) Dispersion curves for first mode Love

waves. Group velocity, u, is shown as solid lines for

continental and oceanic paths. Inferred phase velocity

for continental paths is shown as a broken line, with free

oscillation data above 750 s. Figure based on Oliver (1962).

16.6 FREE OSCILLATIONS 255

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C16.3D

–

256

– [239–266] 13.3.2008 11:41AM

the superposition of oppositely travelling sur-

face waves (or, in some cases, multiply reflected

body waves). The resonant frequencies are

related to the phase speeds of the corresponding

surface waves, which are self-selected so that an

integral number of wavelengths fits into the

Earth. They therefore give a global average of

the same information as the surface waves.

Frequencies of more than 550 modes of free

oscillation have been identified in seismic

records (Masters and Widmer, 1995), providing

a data set for Earth model studies that is inde-

pendent of body wave travel times.

Many of the familiar names of classical

physics and mathematics contributed to the

theory of the vibrations of a sphere, notably

S. D. Poisson, Lord Kelvin, H. Lamb, A. E. H. Love

and Lord Rayleigh. Thus, it has been recognized

for more than a century and a half that the Earth

must have free modes, but for most of that time

there was little expectation of observing them.

There was also a problem that precise calcula-

tions of numerous mode periods for realistic

Earth models would have been quite forbidding

without electronic computers.

Interest in the subject was renewed in the

1950s by H. Benioff’s development of an instru-

ment to observe very long-period seismic waves.

Most seismometers are inertial instruments,

involving suspended masses that can be made

sensitive to very long-period waves only with

great difficulty. Benioff’s instrument was a strain

seismometer, a long quartz tube suspended in a

tunnel, with one end fixed to the ground and the

other attached to a displacement sensor to detect

strain of the ground relative to the unstrained

quartz. Such an instrument has a sensitivity to

ground strain that is independent of wave period,

subject only to a high frequency limit imposed by

mechanical resonances in the mounting and by

electronic response times.

From an examination of a record obtained

immediately after a major earthquake in

Kamchatka in 1952, Benioff tentatively identi-

fied an oscillation with an approximately 57

minute period as a fundamental mode of free

oscillation. His report stimulated both instru-

mental and theoretical developments, so that,

when the next really great earthquake occurred,

in Chile in May 1960, several seismological

research groups were able to record the oscilla-

tions that followed. The Benioff strain meter at

the California Institute of Technology was most

sensitive to toroidal oscillations, while across

town at the University of California Los Angeles

a tidal gravity meter (Slichter, 1967) recorded

spheroidal oscillations but was insensitive to tor-

oidal modes, for which there is no radial motion.

Meanwhile Alterman et al. (1959) had calculated

the frequencies of three modes, and some of

their overtones, for several realistic earth mod-

els. Later in 1960, representatives of several

groups met at an International Union of

Geodesy and Geophysics (IUGG) meeting in

Helsinki. Their observations agreed both with

one another and with theory so well that a new

branch of seismology was established on the

basis of records of a single earthquake. Some of

the mode frequencies were seen to have fine

structure, a splitting of spectral lines due to

rotation, ellipticity and heterogeneity of the

Earth. The similarity to optical spectroscopy, in

which spectral lines may be split by a magnetic

field (the Zeeman effect), led to use of the expres-

sion terrestrial spectroscopy for free oscillation

studies.

Another great earthquake occurred in Alaska

in 1964 and the free oscillation records from

both events (Fig. 16.10) were used to develop

the first of a new generation of Earth models.

Continued improvements in instrumentation, in

data analysis and in methods of interpretation

led to identification of a very large number of

modes and to the use of records from smaller

earthquakes. Evidence of continuous excitation

of fundamental spheroidal modes was first

reported by Nawa et al. (1998), on the basis of a

superconducting gravity meter record from a

quiet station in Antarctica and promptly con-

firmed by several other groups. In this case

oceanic–atmospheric excitation is indicated

(Rhie and Romanowicz, 2004). The use of free

mode periods in model studies in the late 1960s

and 1970s became so effective that little further

improvement in our knowledge of the broad

scale Earth structure can now be expected. The

appearance in 1981 of PREM (Appendix F), the

most widely used global model since that time,

256 SEISMIC WAVE PROPAGATION