Stacey F.D., Davis P.M. Physics of the Earth
Подождите немного. Документ загружается.

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C16.3D
–
257
– [239–266] 13.3.2008 11:41AM
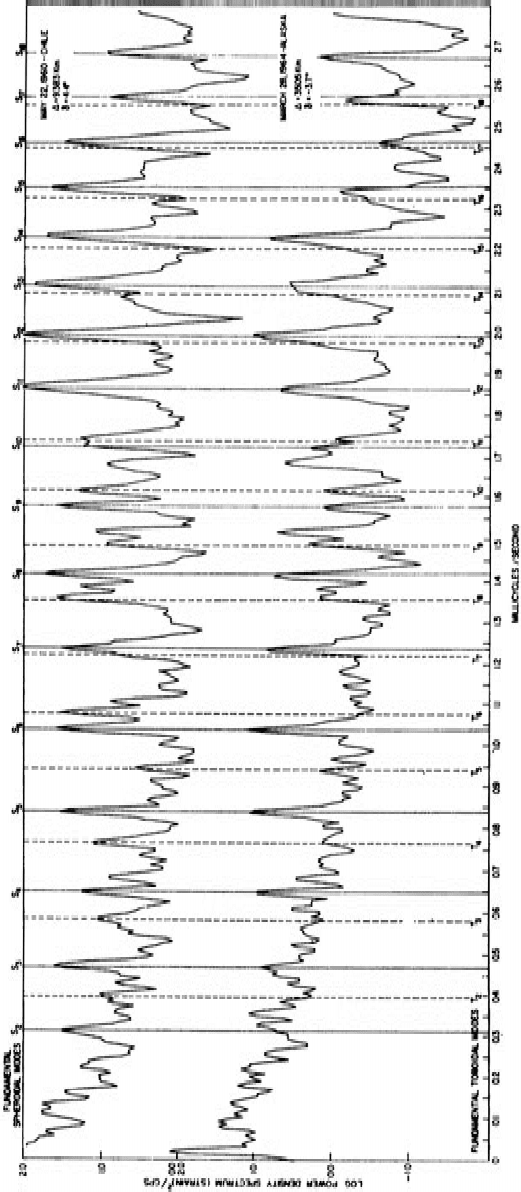
FIG U R E 16.10 Spectra of Earth strain recorded at Isabella, California, for the Chilean 1960 and Alaskan 1964 earthquakes. is the angle between the
strain seismometer axis and the great circle path to the epicentre. Reproduced, by permission, from Smith (1967).
//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C16.3D
–
258
– [239–266] 13.3.2008 11:41AM
signalled a change in scientific direction. At least
in the mantle, lateral variations in structure now
attract more attention than further refinements
of the spherically averaged model, although
equation of state studies (Chapter 18) have
reached the point that an improved model is
needed.
As mentioned above, there are two funda-
mentally different kinds of oscillation, spheroi -
dal (S) and toroidal (T). In both cases the patterns
of surface deformation take the form of sphe-
rical harmonic functions (Appendix C), which
appear in solutions of the seismic wave equa-
tion in spherical geometry (Eq. (C.3)). The sim-
plest to envisage are the radial modes, a special
case of spheroidal oscillations in which the
motion is purely radial. They are alternating
dilations and compressions of the whole Earth
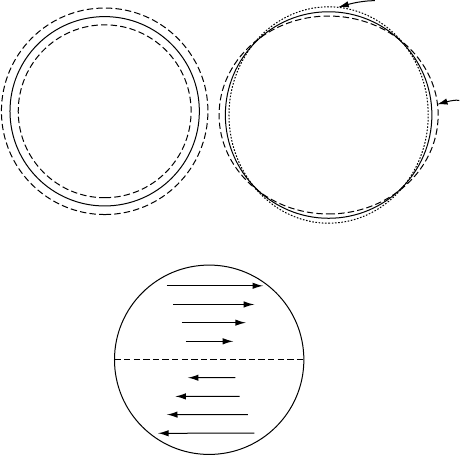
(Fig. 16.11(a)), designated
0
S
0
;
1
S
0
;
2
S
0
... wit h
spherical nodal surfaces within the Earth, the
instantaneous motion being opposite in adja-
cent layers. The prefix gives the number of
these nodal surfaces and the following sub-
script is t he number of nodal line s on the sur-
face, that is the harmonic degree, l,ofthe
surface pattern.
The slowest mode is
0
S
2
(Fig. 16.11(b)), with a
54-minute period. This has been called the foot-
ball mode, because the ellipsoidal deformation
of the Earth alternates between prolate and
oblate. There is no
0
S
1
mode, because that
would imply oscillation of the whole Earth
mass, but
1
S
1
occurs, the internal motion being
opposite to that of the outer shell. An infinite
series of fundamental spheroidal modes
0
S
l
each
has an infinite series of overtones
n
S
l
. The
general case,
n
S
m
l
, involves a tesseral harmonic
deformation of the surface in the form
P
m
l
cos ðÞcos ml (see Appendix C), but the fre-
quencies are almost the same for different values
of m with the same l and n. They would be iden-
tical for a non-rotating, spherically layered
Earth, but this degeneracy is broken by rotation,
causing the line splitting mentioned earlier.
Ellipticity and lateral heterogeneity give smaller
contributions to the line splitting. The splitting
decreases with mode frequency and is important
only for the low degree modes. The superscript
m is generally omitted in referring to free oscil-
lation modes.
Of the toroidal modes,
0
T
2
(Fig. 16.11(c)) is the
simplest, being an alternating twist between two
Prolate
Oblate
(a) (b)
(c)
FI G U R E 16.11 The simplest
representative modes of free oscillation.
(a) Radial oscillation
0
S
0
. (b) Spheroidal
‘football’ mode
0
S
2
. (c) Instantaneous
angular motion in toroidal mode
0
T
2
.
258 SEISMIC WAVE PROPAGATION

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C16.3D
–
259
– [239–266] 13.3.2008 11:41AM
hemispheres. Higher modes involve the subdivi-
sion of the surface motion into 3, 4, ..., l zones
and, as with spheroidal oscillations, there are
overtones with internal nodal surfaces, whose
number is given by the prefix n. As in the case
of spheroidal oscillations, modes represented
by tesseral harmonics have almost the same
frequencies as zonal harmonics of the same
degrees.
The spheroidal modes are standing Rayleigh
waves and the toroidal modes are standing Love
waves in spherical geometry. A particular
advantage in analysing surface waves by free
mode theory is that the sphericity of the Earth
is properly accounted for. Clearly this is more
important for the longer wavelengths and is
essential at the longest wave periods in Fig. 16.9.
The surface patterns of free oscillation
motions are spherical harmonics, as mentioned
above. However, the coordinate axes are not the
geographic axes but are controlled by the loca-
tions and fault orientations of the exciting earth-
quakes. Thus, any particular observatory lies
close to some nodal lines for one earthquake,
but to a different set after another earthquake.
When this geometrical variation is allowed for,
estimation of the relative excitation amplitudes
of the various modes gives information about the
earthquake mechanisms. For this purpose the
amplitudes should be extrapolated back to a
time immediately after an earthquake as there
is a westward drift of the nodal pattern that can
confuse amplitude observations for the lower
modes. This drift must be recognized also in
using amplitude decay as a measure of damping.
The nodal drift is related to the mode splitting
and arises from the slightly different phase
speeds of eastward and westward propagating
waves in the rotating Earth.
Early Earth models, developed by K. E. Bullen,
used the seismic wave velocities, V
P
and V
S
, con-
straining the density structure to match the total
mass and moment of inertia. Since the 1960s,
Earth models have increasingly relied on the
frequencies of the modes of free oscillation.
The torsional modes involve only horizontal
motion, but the spheroidal modes involve
changes in shape, with radial motion and there-
fore gravitational as well as elastic restoring
forces. This means that they provide an independ-
ent fix on the density structure. We can under-
stand this in terms of a simplified model that is
amenable to elementary calculus, a homoge-
neous sphere subject to self-gravitation, with den-
sity and elasticity uniform throughout, ignoring
the effect of the steady internal compression.
Consider the spheroidal mode
0
S
2
, an oscilla-
tion with alternating prolate and oblate ellipsoi-
dal deformations. Using cylindrical coordinates,
with the origin at the centre and axes z along the
symmetry axis, r in the perpendicular plane and
the angle to the z axis, the surface deformation
has the form of the zonal harmonic P
2
(cos )
(Appendix C) and is given by
¼ aP
2
sin !t ¼ a ð 3=2 cos
2
1=2Þsin !t; (16:52)
for which the maximum axial elongation is a,
with corresponding maximum radial contraction
a/2. We calculate the frequency of the oscilla-
tion, !, by using the fact that the total energy is
conserved, being entirely kinetic energy, E
K
,at
the instants of zero deformation and entirely
potential energy of elastic strain, E
S
, and dis-
placement of mass in the gravity field, E
G
,at
the instants of maximum deformation. Thus
E
K
¼ E
S
þ E
G
: (16:53)
E
G
has a simple form. The energy of elevation
by distance of any surface element dA, relative
to the undeformed radius, R, is (1/2)g
2
dA
because mass dA is elevated by an average dis-
tance /2 against gravity g. Areas for which is
negative are included by noting that the missing
mass below R can be considered raised to R and
then transferred to the areas of positive . Thus,
with given by Eq. (16.52), at sin !t ¼1,
E
G
¼
1
2
g
ð
2
dA ¼
1
2
ga
2
ð
p
0
3
2
cos
2
1
2
2pR
2
sin d
¼
2p
5
R
2
ga
2
:
(16:54)
With substitution for g by g ¼GM/R
2
¼(4/3)pGR,
E
G
¼
8p
2
15
GR
3
2
a
2
: (16:55)
16.6 FREE OSCILLATIONS 259

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C16.3D
–
260
– [239–266] 13.3.2008 11:41AM
At maximum deformation the strain can be
represented as two perpendicular shear strains,
each with the form of Fig. 16.11(b). Each compo-
nent of strain gives an extension by a/2 in the axial
direction and a/2 in the equatorial plane with
the equatorial strains at right angles to one
another, so that there is a uniform contraction
a/2 in all directions in the equatorial plane and
total extension a of the axis. Thus, we consider two
perpendicular shear strains, each of magnitude
" ¼ a=R,thatareuniformthroughoutthevolume
V of the sphere, and the strain energy is
E
S
¼ 2
1
2
"
2
V ¼
4
3
pRa
2
: (16:56)
In calculating the kinetic energy, E
K
,we
resolve the motion into axial (z) and radial (r)
directions, in which the amplitudes of the motion
are az/R ¼a cos and (1/2)ar/R ¼(1/2)a sin respec-
tively. There is no radial motion on the axis and
no axial motion in the equatorial plane. For
sinusoidal motion at angular frequency !, the
maximum particle velocities in the axial and
radial directions are a! cos and (1/2)a! sin ,
and since they are mutually perpendicular,
their contributions to the energy are simply
added. For an elementary volume dV the ener-
gies are dE
z
¼(1/2)(a! cos )
2
dV and dE
r
¼(1/8)
(a! sin )
2
dV. To integrate the axial component
we divide the sphere into elementary discs of
radius R sin and thickness dz ¼R sin d at
z ¼R cos , so that dV ¼pR
3
sin
3
d and
E
z
¼
ð
p
0
1
2
ða! cos Þ
2
pR
3
sin
3
d
¼
2p
15
R
3
!
2
a
2
:
(16:57)
To integrate dE
r
we divide the sphere into ele-
mentary cylinders of thickness dr ¼R cos d and
length 2z ¼2Rcos ,sothatdV¼4pR
3
cos
2
sin d,
giving
E
r
¼
ð
p=2
0
1
8
ða! sin Þ
2
4pR
3
cos
2
sin d
¼
15
p
R
3
!
2
a
2
; ð16 :58Þ
and therefore
E
K
¼ E
z
þ E
r
¼ðp=5ÞR
3
!
2
a
2
: (16:59)
Substituting for E
G
, E
S
and E
K
by Eqs. (16.55),
(16.56) and (16.59) in Eq. (16.53), we have
!
2
¼
8p
3
G þ
20
3
R
2
: (16:60)
Recognizing that the shear wave speed is
V
S
¼ð=Þ
1=2
and that the travel time for a
shear wave across a diameter is T ¼2R/V
S
,we
can write the period, ¼2p/!, of the
0
S
2
mode
for a uniform sphere as
¼
2
3p
G þ
20
3p
2
1
T
2
1=2
: (16:61)
In the absence of the gravity term this would be
1.217T, that is the mode period would be com-
parable to the shear wave travel time across a
diameter. But the important thing to notice
about this equation is that, with inclusion of
the gravity term, density enters the equation
for independently of the travel time or velocity
term. This is the principle that allows the broad-
scale density profile of the Earth to be obtained
from spheroidal mode periods. For a fluid body
( ¼0), the gravity term is the only one on the
right-hand side of Eqs. (16.60) and (16.61). The
Sun is such a body and observations of its free
modes (helio-seismology) provide information
about its internal structure, but in this case the
assumption of homogeneity is a very poor one.
We can use a similar analysis to calculate the
period of the
0
T
2
mode for a homogeneous
sphere. The torsional modes involve no radial
motion and so give no independent information
about density, but this means that they give
details of the / structure without the compli-
cation of G terms, such as appear in Eqs. (16.60)
and (16.61), and so help in isolating the gravita-
tional effect on the spheroidal modes.
0
T
2
is the
simplest torsional mode, being a twisting
motion between two hemispheres, with the
equatorial plane of the motion as a node. The
angular displacement increases linearly with
distance from this plane in the manner of the
first degree zonal harmonic P
1
(cos ) ¼cos ¼
z /R. Dividing the sphere into discs of radii
r ¼R sin and thickness dz ¼R sin d,asinthe
260 SEISMIC WAVE PROPAGATION

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C16.3D
–
261
– [239–266] 13.3.2008 11:41AM
calculation of E
z
above, each disc has a mass
dm ¼pR
3
sin
3
d and moment of inertia
dI ¼(1/2)r
2
dm ¼(p/2) R
5
sin
5
d. Taking the
maximum angle of twist at the pole of the
motion to be w, and therefore wz=R ¼ w cos at
co-latitude , the maximum angular velocity of
an elementary disc about its axis is !w cos and
its kinetic energy is ð1=2ÞdIð!w cos Þ
2
. Thus, the
total kinetic energy is
E
K
¼
1
2
ð
p
0
ð!w cos Þ
2
dI
¼
p
4
R
5
w
2
!
2
ð
p
0
cos
2
sin
5
d
¼
4p
105
R
5
w
2
!
2
:
(16:62)
Now we calculate the strain energy at an instant
of maximum twist between the hemispheres. Each
disc, of thickness dz ¼R sin d,istwistedbyan
angle dw ¼ wdz=R ¼ w sin d.Wecanusethisin
the standard formula for the torsional constant of a
rod of radius r and length l, that is the torque
per unit of angular twist, ¼ðp=2Þr
4
=l,with
l ¼dz ¼sin d, and write the strain energy as
dE
S
¼ð1=2ÞðdwÞ
2
¼ðp=4ÞR
3
w
2
sin
5
d;
(16:63)
which integrates to
E
S
¼ð4p=15ÞR
3
w
2
: (16:64)
Now we can equate Eqs. (16.62) and (16.64) to
give
!
2
¼ 7=R
2
: (16:65)
Rewriting this as the oscillation period, ,in
terms of the travel time of a shear wave across
a diameter, T ¼ 2Rð=Þ
1=2
;
¼ðp=
p
7ÞT ¼ 1:19T: (16:66)
This is very close to the
0
S
2
period if the gravita-
tional term in Eq. (16.61) is neglected. With
inclusion of this term the
0
S
2
mode would be
faster, but for the Earth it is significantly slower,
at least partly because radial motion in the fluid
core imparts inertia to the system, but there is
little corresponding slowing of
0
T
2
.
16.7 The moment tensor and
synthetic seismograms
Calculation of the normal modes of the Earth is
similar to calculating those of a stretched string
(or rod), with the one-dimensional geometry
replaced by the three-dimensional geometry of
the Earth. In the case of the string, the eigenfunc-
tions are sinusoids in space that satisfy the boun-
dary condition of zero displacement at the ends,
between which there is an integral number of
half wavelengths, allowing a series of discrete
frequencies. For the Earth the corresponding
boundary conditions are zero tractions on the
surface. The eigenfunctions or normal modes
are spherical Bessel functions that describe the
radial variation, and spherical harmonics for vari-
ation over spherical surfaces. Each mode has a
distinct frequency determined by the boundary
condition. In the general case, the displacement
field can be expressed as a weighted sum of
normal modes with weights adjusted to satisfy
the initial conditions of excitation. For an ea rth-
quake the normal mode displacements at time
zero mu st match the dislocation d escribed by
the earthquake moment tensor, which, as dis-
cussed in Chapter 14, can be expressed in terms
of force couples. The displacement from a force
couple was obtained by differentiating the dis-
placement field from a point force wi th resp ect
tothesourcelocation(Eq.(14.9)).Thus,ifwe
solve for the normal modes generated by appli-
cation of a point force within the Earth, we can
synthesize the modes generated b y any arbi-
trary moment tensor by ta king appropriate
derivatives and superimposing the solutions.
The resulting displacement field gives synthetic
seismograms at any place and time on the globe
with due account for sphericity and variation
with depth.
We illustrate the excitation of normal modes
by a point force by examining the one-dimensional
case of longitudinal oscillations of an elastic rod,
fixed at x ¼0 and x ¼L, with displacement u in
the x-direction (Fig. 16.12). The normal modes
are given by
u
n
¼ sinð!
n
x=cÞexpði!
n
tÞ; (16:67)
16.7 THE MOMENT TENSOR AND SYNTHETIC SEISMOGRAMS 261
//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C16.3D
–
262
– [239–266] 13.3.2008 11:41AM
with eigenfrequencies
!
n
¼ n
pc
L
; n ¼ 1; 2; 3; ...; (16:68)
where c ¼
ffiffiffiffiffiffiffiffi
E=
p
is the velocity that satisfies the
one-dimensional wave equation, assuming that
the wavelength is much greater than the rod
thickness,
E@
2
u=@x
2
¼ @
2
u=@t
2
; (16:69)
and E and are Young’s modulus and density.
Then
c
2
@
2
u=@x
2
¼ @
2
u=@t
2
: (16:70)
The effect at time t 0 of a disturbance at time
t ¼0, expressed as a weighted sum of normal
modes, is
uðx; tÞ¼
X
i
a
n
u
n
ðx; tÞ¼
X
i
a
n
sinðk
n
xÞ
ð1 expði!
n
tÞÞ; ð16:71Þ
where k
n
¼ !
n
=c and the mode shapes are ortho-
gonal, so that
2
L
ð
L
0
sin
npx
L
sin
mpx
L
dx ¼
mn
¼ 1
if m ¼ n; or ¼ 0ifm 6¼ n;
(16:72)
where m and n are integers. Suppose that at time
t ¼ 0 and location x ¼ x
s
a force f
0
is applied in
the x-direction and is maintained indefinitely. It
can be represented by
f ¼ f
0
ðx x
s
Þ
a
HðtÞ; (16:73)
where f is the force per unit volume, a is the
cross-sectional area of the rod, ðxÞ is a delta func-
tion in x,andHðtÞis a Heaviside step function. The
equation of motion (Eq. (16.69)) becomes
E@
2
u=@x
2
þ f
0
ðx x
s
Þ
a
HðtÞ¼@
2
u=@t
2
: (16:74)
Substitution of Eq. (16.71) for u and solving for
the coefficients a
n
in that equation by taking a
Fourier transform and using Eq. (16.72) to resolve
individual coefficients (Problem 16.3) gives
uðx; tÞ¼
X
i
2f
0
M
sinðk
i
x
s
Þsinðk
i
xÞ
1 cos !
i
t
!
2
i
;
(16:75)
where M ¼ aL is the mass of the rod. Equa-
tion (16.75) can be interpreted as displacement
equals a sum of modes, evaluated at the point
of application of the force, multiplied by the eigen-
functions and the time variation (Fig. 16.13).
We showed in Chapter 14 that dislocations are
equivalent to force couples and doublets. In the
rod case a force doublet corresponds to clamping a
small section of the rod at x
s
in compression and
releasing it at t ¼0. The solution for a force dou-
blet is obtained by placing a second oppositely
directed force a distance dx from x
s
and summing
the solutions. For this case the solution is obtained
by adding to Eq. (16.75) the displacement caused
by a second, oppositely directed force at distance
dx from x
s
. In effect this means differentiating
Eq. (16.75) with respect to x
s
and multiplying by
dx, and is completely equivalent to the differen-
tiation of Eq. (14.8) to produce Eq. (14.9). Following
the procedure in Section 14.2, we replace the force
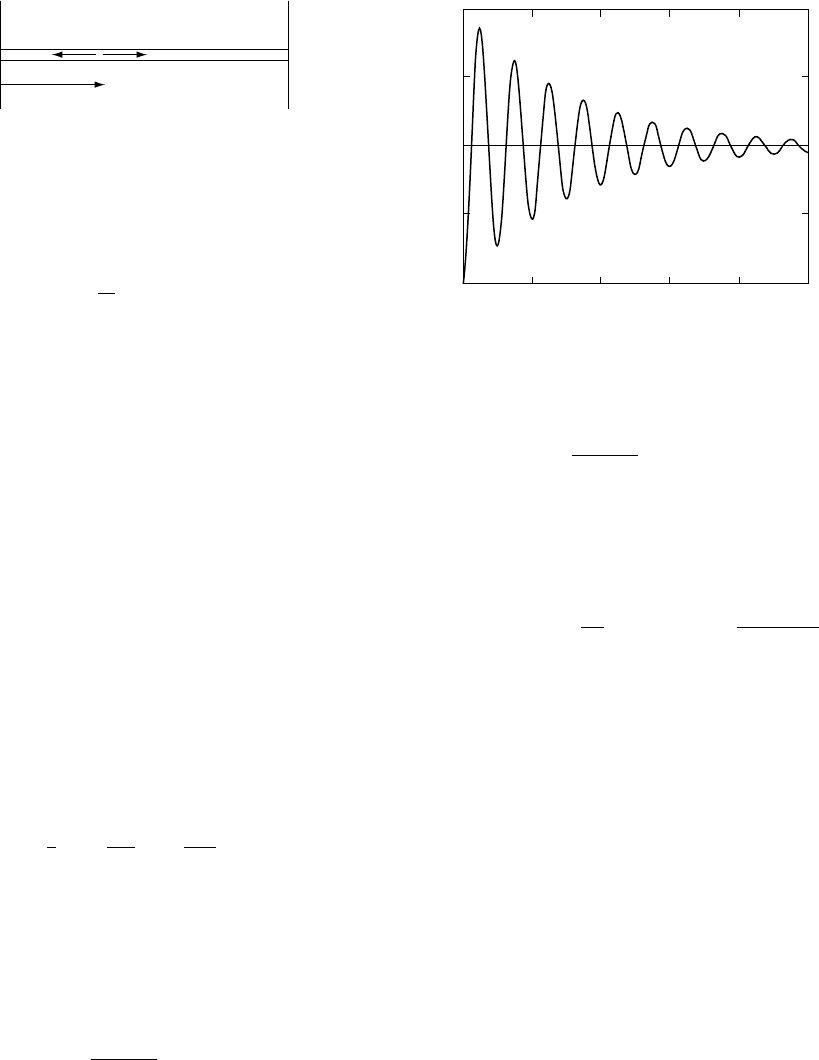
x
s
0
L
FI G U R E 16.12 Geometry of a force doublet excitation
of a clamped rod.
2.0
1.5
1.0
0.5
0.0
0 200 400 600 800 1000
Time
FI G U R E 16.13 Time variation of a normal mode excited
by a source that is a step function at t ¼0.
262 SEISMIC WAVE PROPAGATION
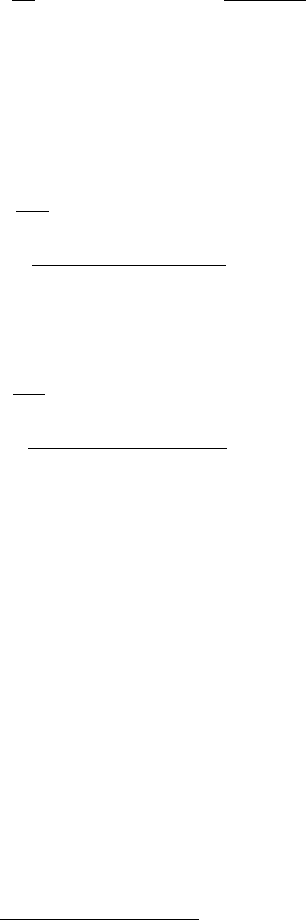
//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C16.3D
–
263
– [239–266] 13.3.2008 11:41AM
moment f
0
dx with dislocation moment Eab ¼ M
0
,
where b is the dislo cation and a the area, to obtain
uðx; tÞ¼
M
0
M
X
i
2k
i
cosðk
i
x
s
Þsinðk
i
xÞ
1 cos !
i
t
!
2
i
;
(16:76)
where, as in Eq. (14.9), we have the moment
term, M
0
, multiplied by the Green’s function,
here expressed as a sum of normal modes. If we
include attenuation,
uðx; tÞ¼
2M
0
M
X
i
k
i
cosðk
i
x
s
Þsinðk
i
xÞ
1 exp½!
i
t=2Q
i
cos !
i
t
!
2
i
:
(16:77)
Note that k
i
cosðk
i
x
s
Þ is the strain @u/@x of the ith
mode or e
i
xx
ðx
s
Þ: Then
uðx; tÞ¼
2M
0
M
X
i
e
i
xx
ðx
s
Þsinðk
i
xÞ
1 exp½!
i
t=2Q
i
cos !
i
t
!
2
i
:
(16:78)
Thus, the weights are equal to the spatial
derivatives of the eigenfunctions, that is, strains
evaluated at the source point x
s
, multiplied
by the corresponding elements of the moment
tensor and divided by mass. Equation (16.78)
describes a force doublet applied to a rod. To
use this approach to describe a dislocation in
the Earth, the one-dimensional eigenfunctions
are replaced with three-dimensional ones. So,
based on Eq. (16.78), we can write down the
solution directly. The displacement field uðx; tÞ
from a point source earthquake with arbitrary
moment tensor M
pq
ðx
s
Þ (Aki and Richards, 2002),
represented as a sum of normal modes, is
uðx; tÞ¼
X
i
e
i
pq
ðx
s
ÞM
pq
ðtÞ
hi
u
i
ðxÞ
1 expð!
i
t=2Q
i
Þcos !
i
t
!
2
i
;
(16:79)
where u
i
ðxÞ is the displacement attributed to the
ith normal mode and e
i
pq
ðx
s
Þ is the corresponding
strain evaluated at the location of the source.
Once the normal modes are calculated,
Eq. (16.79) can be used to calculate the seismic
wave field for an arbitrary moment tensor, M
pq
.
The term on the RHS of Eq. (16.79) represents a
damped sinusoidal oscillation with offset 1=!
2
i
(Fig. 16.13) and so includes the static displace-
ment (offset) of the dislocation. The normal
modes, u
i
ðxÞ, depend on the Earth model,
and are found by satisfying the equation of
motion and the boundary conditions of continu-
ity of stress and displacement at each layer boun-
dary including the surface. Calculation of the
modes has progressively improved with refine-
ments to take into account gravity, the rotation
of the Earth, its ellipticity, and lateral hetero-
geneity.
Equation (16.79) is used in inversion of seis-
mic data to determine M
pq
. This is the basis of
the Harvard moment tensors that have been
calculated worldwide since about 1977 for
earthquakes above magnitude 5.6. By adding a
sufficient number of normal modes one obtains
all the transient waves that radiate from a
source, including all body waves and surface
waves (Fig. 16.14). In that they can all be rep-
resented as normal modes, the distinction
between body and surface waves and free oscil-
lations is a matter of timing as to when the
observations are made. The transient waves
can only be observed early in the record, while
they remain isolated from other phases. As time
progresses multiple reflections and transmis-
sions around the globe and dispersion of wave
trains cause the energy to merge into a contin-
uous global vibration, which is better analysed
in the frequency domain for mode peaks and
attenuation. A fast method of calculating modes
(Woodhouse 1983, 1988) is capable of modell-
ing body wave phases at frequencies up to
0.16 Hz. However, in practice the moment ten-
sor obtained from normal modes is largely
made up of waves with periods much longer
than the earthquake duration, and so is repre-
sentative of the moment distribution averaged
in time and space, referred to as the centroid
moment tensor. In contrast, the moment deter-
mined from first-arriving P-body waves meas-
ures fault motion at the hypocentre, which,
unless the event expands symmetrically, will
be offset from the centroid.
Normal mode eigenfunctions (Fig. 16.15) show
how the different frequencies give a weighted
16.7 THE MOMENT TENSOR AND SYNTHETIC SEISMOGRAMS 263

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C16.3D
–
264
– [239–266] 13.3.2008 11:41AM
sampling of the Earth’s internal structure. From
Eq. (16.75) we see that the excitation of a mode
depends on its strain calculated at the location of
the earthquake. Earthquakes near the surface
excite fundamental modes which have their
eigenfunctions concentrated near the surface.
Deep earthquakes excite higher-order modes or
overtones with weaker excitation of fundamen-
tal modes.
Of particular interest are the modes that have
significant energy in the inner core, and have
played an important role in confirming the solid-
ity of the inner core. As early as 1946 Bullen used
the amplitudes of reflected P-waves from
the inner core surface, but the inference that it
represents a liquid–solid interface required
several assumptions. The reflection coefficient
depends on the impedance (V
P
) contrast
(Eq. (16.29)). Independent evidence from travel
times for P-waves suggested that the contrast
was caused by a significant increase in V
P
from
outer to inner core rather than a density change.
The jump in V
P
could be explained if the inner
core is solid, so that the P-wave modulus changes
from ¼ K
outer
to ¼ K
inner
þ
4
3
(Eq. (16.1)).
Alternatively, if the inner core remained liquid
the required change in K was unreasonably large,
and a decrease in density with depth is implau-
sible. However, the definitive test required
identification of inner core shear waves.
Because the outer core is fluid, the shear waves
have to be generated by conversions of P-waves
at the inner core boundary. Such conversions are
inefficient because incident angles are small.
Furthermore, as we mention below, S-waves
appear to be highly attenuated in the inner
core. After passage though the inner core they
convert back to P-waves, which must be distin-
guished from other phases that might arise from
heterogeneities in the mantle. Thus, early
reports of inner-core S-body wave phases (such
as PKJKP) have been questioned to the point that
skepticism was expressed as to whether they
would ever be observed in high frequency body
waves (Doornbos, 1974). Analysis of normal
modes can overcome these problems, because,
rather than relying on identification of indi-
vidual weak S phases, the mode energy is
R
1
R
2
R
3
R
1
R
2
G
3
G
2
G
1
FI G U R E 16.14 Synthetic seismograms from normal mode summations compared with observations. The top traces
are the observations and the bottom traces the synthetics for three earthquakes measured at the seismic station
ANMO in Albuquerque, New Mexico. From Woodhouse and Dziewonski (1984). R
1
,R
2
, ...are Rayleigh waves from the
short and great circle paths from the source to the station. G
1
,G
2
, ... are the corresponding Love waves.
264 SEISMIC WAVE PROPAGATION

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C16.3D
–
265
– [239–266] 13.3.2008 11:41AM
effectively stacked by spectral analysis of
long wave-trains. Modes having eigenvectors
with significant particle motions in the
inner core (
6
S
2
and
7
S
3
) indicated an average
V
S
¼ 3:52 0:03 km=s (Masters and Gilbert,
1981). This apparently low value is expected for
solid iron at inner-core pressure, as explained in
Section 18.8. Now that anisotropy is recognized
(Section 17.7), we know that the inner core is
crystalline and aligned.
FI G U R E 16.15 Eigenfunctions of toroidal and spheroidal normal modes from the surface to the core–mantle
boundary (Dahlen and Tromp, 1998). (a), (b) and (c) show torsional modes. (d) shows spheroidal modes, with solid
lines representing radial displacements and dashed lines tangential displacements.
16.7 THE MOMENT TENSOR AND SYNTHETIC SEISMOGRAMS 265
//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C16.3D
–
266
– [239–266] 13.3.2008 11:41AM
The usefulness of mode-generated synthetic
seismograms was illustrated in a resolution by
Deuss et al. (2000) of the debate over identifica-
tion of phases propagating as shear waves in the
inner core (in the notation illustrated by
Fig.17.7, PKJKP, SKJKP and also pPKJKP, which
has a surface reflection from a deep event).
These phases have very small amplitudes
because the necessary P to S and S to P conver-
sions of the inner core boundary are weak; addi-
tionally Doornbos (1974) pointed out that the
low Q for S-waves would make them completely
unobservable at high frequencies (1 Hz) and
reported observations have been disputed.
Using a method of phase stacking records from
the deep 1996 Flores Sea event, Deuss et al.
(2000) compared observed arrivals at the
expected times with synthetic seismograms for
the PREM model. They repeated the calculation
of synthetics for a modified PREM, with no inner
core shear wave but the same V
P
. By accepting
only arrivals seen with the solid inner core model
but not the fluid model, they were able to dis-
criminate against interfering minor signals from
the mantle. Superimposed pPKJKP and SKJKP
arrivals survived this test, but a similar analysis
for a deep 1994 Bolivia event found no unambig-
uous evidence for inner-core S-waves. Although
the Flores Sea event provided the only body wave
evidence for inner-core rigidity, it confirmed the
average V
S
3:6km=s inferred from free oscilla-
tion modelling.
266 SEISMIC WAVE PROPAGATION
