Stacey F.D., Davis P.M. Physics of the Earth

Подождите немного. Документ загружается.

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C17.3D

–

267

– [267–293] 13.3.2008 2:15PM

Seismological determination

of Earth structure

17.1 Preamble

Our knowledge of the Earth’s internal structure

would almost certainly be very primitive if there

were no earthquakes. Explosive sources of elas-

tic waves would have been recognized and it is

possible that exploration seismology, directed to

the identification of oil-bearing structures in the

crust, would have been well developed, but it is

likely that deep-Earth seismology would have

been rudimentary. The larger nuclear weapons

tests generate waves of sufficient amplitudes to

be detected at remote stations, but recognition

of the test-monitoring possibilities of seismology

depended on the fact that the subject was

already well developed when nuclear testing

began. Even if the weapons-testing agencies

had appreciated the seismic detection possibil-

ities, a shroud of secrecy would have ensured

that evidence of deep Earth structure emerged

only very slowly.

This hypothetical situation emphasizes how

completely our detailed knowledge of the deeper

parts of the Earth relies on observations of seis-

mic waves. Quantitative instrumental data on

teleseismic waves (from distant earthquakes)

were first obtained in the late nineteenth century

and, as the theory of elastic waves was then

already well established, seismology developed

rapidly. The use of earthquake-generated waves

to study the Earth’s interior is a mature and

sophisticated science, to which this chapter is

necessarily only a brief introduction. Comprehen-

sive treatments are by Bullen and Bolt (1985), Aki

and Richards (2002) and Stein and Wysession

(2003).

As we now know, the Earth’s internal layers,

as well as the surface, are close to oblate ellip-

soids, symmetrical about the rotational axis. It is

not an entirely trivial matter to establish that

this is true. Major earthquakes occur in limited

bands around the Earth and these bands obvi-

ously differ in some respects from the larger

non-seismic areas. Also seismometers are almost

all placed on land, so that there is a danger of a

systematic bias in the observations. It would be

very difficult to ensure that a seismological

model based entirely on body waves is not

affected by such bias. However, surface waves,

propagating around the Earth on paths that may

be predominantly either continental or oceanic,

give information about lateral heterogeneity,

complementary to that obtained from the body

waves that penetrate the deep interior. At the

lowest frequencies, free oscillations of the

entire Earth are observed and they directly indi-

cate average properties. Average models are nor-

mally represented by radial variations in

properties for a sphere, although derived by

assuming elliptical internal surfaces. Thus, we

are confident of the reliability of recent global

average Earth models, the most widely used of

which is PREM (Preliminary Reference Earth

Model (Dziewonski and Anderson, 1981), see

Appendix F). Departures of the real Earth

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C17.3D

–

268

– [267–293] 13.3.2008 2:15PM

average from PREM are probably less significant

than the local and regional variations that have

now become subjects of study.

Early Earth modelling, notably the pioneer-

ing work of K.E. Bullen in the 1930s, used

body wave travel times to obtain the variations

of P- and S-wave speeds through the Earth

(Section 16.6). These give the ratios of elastic

moduli to density, and additional information

was required to estimate density independently.

Using the known mass and moment of inertia of

the Earth with the assumption of simple adia-

batic compression with depth where the wave

speeds indicated that this was reasonable, Bullen

obtained Earth models that are remarkably close

to our present understanding. The most impor-

tant additional data available for the develop-

ment of recent Earth models are the periods of

free oscillation (Section 16.6). The spheroidal

modes, which involve radial motion, have grav-

itational as well as elastic restoring forces and so

give independent evidence of density structure.

There are also torsional or toroidal modes that

give strong control on the shear wave structure

in Earth modelling.

To account for the properties of the deep

regions of the Earth, we must allow for the

changes in these properties that are caused by

the high pressures. For a homogeneous layer, seis-

mology itself provides a method of doing this. The

ratio K

/ ¼(@P/@)

¼(V

(4/3)V

)isobtained

directly from the wave speeds and if density every-

where is adequately modelled, so that gravity var-

iation is determined by the model, then so is the

density gradient (Section 17.5). This is most

precisely true for the outer core, for which

homogeneity is assured by three-dimensional

stirring at speeds of tens of kilometres per year,

as evidenced by the geomagnetic secular varia-

tion (Section 24.3). This ensures not just homo-

geneity but an adiabatic temperature gradient,

so that compression is described by the adiabatic

modulus, K

, derived from the wave speed.

Theories that account for the strong variations

in density and bulk modulus with pressure are a

subject of Chapter 18.

The broad-scale layering of the Earth, out-

lined by seismology, represents the average and

stable state of the internal structure. Finer

details, lateral variations and anisotropy, are

attributed to the dynamic behaviour and must

change slowly with time. They are most clearly

observed in the crust and uppermost mantle but

are recognized to occur at all depths in the man-

tle. This is a new frontier of the subject. It is

obvious that the Earth must be laterally hetero-

geneous in the uppermost 100 km or so where

surface waves propagate, because surface waves

from an earthquake are not sharply re-focussed

to cause damage at an anti-focus on the opposite

side of the Earth. But heterogeneities occur

throughout the mantle and are generally believed

to be related to the tectonic pattern. Observations

become less detailed with depth, and in the lower

mantle we are confident that there are features

such as plumes and fragments of subducted slabs

that have not yet been resolved seismologically.

However, in the D

layer, the lowermost 200 km

or so of the mantle, strong lateral heterogeneities

are well documented. In Chapter 12 these are

referred to as crypto-continents and crypto-oceans,

by analogy with the surface structure (see Fig. 12.3),

but are probably to be explained, at least partly, by

a phase transition to the post-perovskite mineral

structure, referred to in Section 2.7.

The ellipticity of the core is not well con-

strained by seismological observations and this is

even more true of the inner core. Evidence from

very long baseline interferometry (VLBI) observa-

tions of the nutations suggest that the core is more

elliptical than equilibrium theory suggests, as

mentioned in Section 7.5. There is a strong reason

to expect a non-equilibrium ellipticity of the inner

core. It is likely that solidifying material is prefer-

entially deposited on the equator, giving the inner

core an excess ellipticity from which it deforms

towards its equilibrium flattening. Crystal align-

ment resulting from the deformation is the most

plausible explanation for the inner core aniso-

tropy (Yoshida et al., 1996; see Section 17.9).

17.2 Refraction in a plane layered

Earth

For seismic wave propagation over distances

that are small compared with the radius of

268 SEISMOLOGICAL DETERMINATION OF EARTH STRUCTURE

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C17.3D

–

269

– [267–293] 13.3.2008 2:15PM

the Earth, the sphericity has little effect on

travel times. A model in which wave speed

increases with depth in a series of plane, hori-

zontal layers is a useful approximation to real-

ity in some situations. It is also a convenient

starting point for a more general discussion of

travel times.

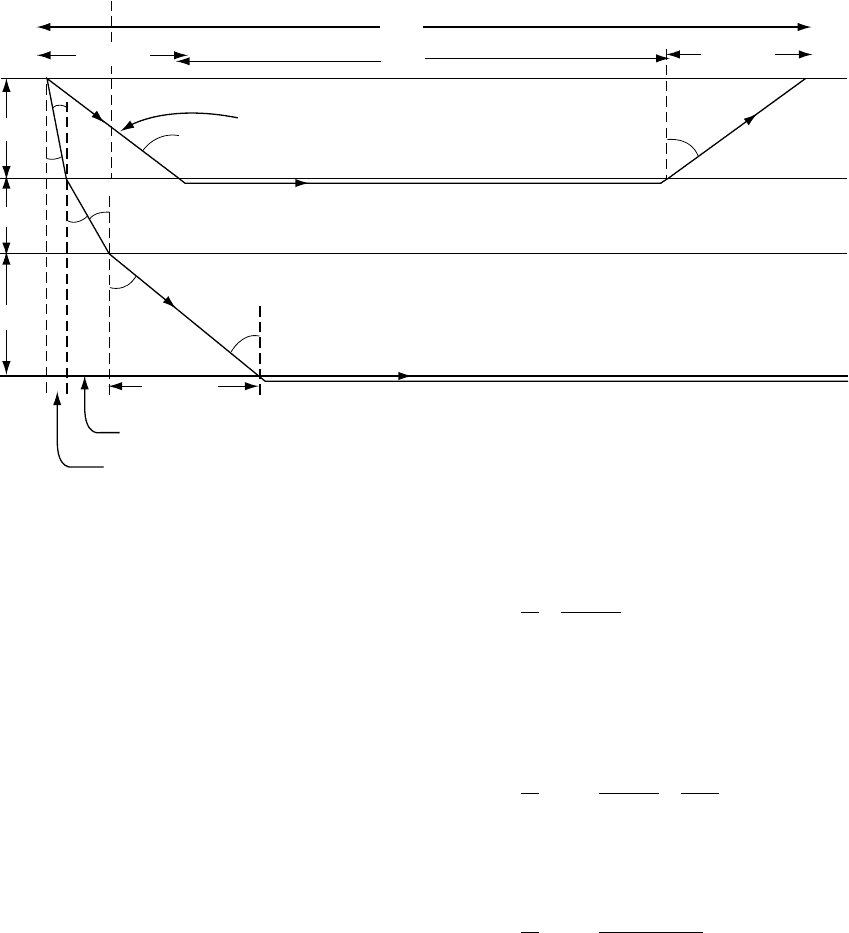
Consider the model in Fig. 17.1, in which two

of the possible seismic rays from an earthquake

or explosion are shown. The shallower ray just

penetrates layer 2, being refracted horizontally

within it. Since this means that the angle of

refraction from the boundary with layer 1 is

908, Snell’s law (Eq. (16.5)) gives the angle of

incidence, , in terms of the ratio of wave speeds

in the two layers,

sin  ¼ V

: (17:1)

Then the distance travelled in layer 2, at speed

, is related to the total distance, S, and the

thickness, z

, of layer 1,

x ¼ S  2z

tan : (17:2)

The total travel time for this ray is the sum of

times in the two layers

T ¼

cos 

; (17:3)

so that, substituting for x by Eq. (17.2), we obtain

the T(S) relationship for a family of rays that

penetrate layer 2 but no deeper and travel to

various distances S:

T ¼

þ 2z

cos 



tan 



: (17:4)

With substitution for  by Eq. (17.1), this

becomes

T ¼

þ 2z



 V



1=2

: (17:5)

For this family of rays the travel time is linear

in S, at speed V

, but with an intercept due

to layer 1.

The analysis is readily extended to a multi-

plicity of layers. If the deepest layer penetrated

by a family of rays has speed V

, then this is the

speed across the surface of the wave arrivals of

this family, and the angles to vertical of the rays

in each of the higher layers are

/cos θ

tan θ

tan i

tan θ

FI G U R E 17.1 Geometry of seismic rays in a plane layered Earth model, having P-wave speed, V

, progressively

increasing with depth. Waves that travel for much of their paths in deeper and faster layers, as illustrated, are known

as head waves.

17.2 REFRACTION IN A PLANE LAYERED EARTH 269

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C17.3D

–

270

– [267–293] 13.3.2008 2:15PM

sin i

¼ V

; sin i

¼ V

; ... (17:6)

Using these angles to write down the travel time

and horizontal distance of travel for each of the

layers, as for the single layer, we arrive at the

general result

T ¼

þ 2

n1

j¼1

 V



1=2

: (17:7)

As before, this is a linear relationship, but with

an intercept that depends on the depths and

speeds of all of the higher layers. Thus, to deter-

mine these parameters from a listing of travel

times, as in Problem 17.2 of Appendix J, one can

first obtain all the speeds from the series of gra-

dients of the travel-time curve, and then use the

intercepts to find the layer thicknesses in turn,

starting from the top.

In such an exercise it is necessary to note that

travel times from a near source generally give

only the time of travel of the first arriving pulse

at each of a series of recording stations. Thus, for

the nearest stations the first wave has travelled

in the top layer and only beyond a certain dis-

tance does a ray that has reached layer 2 arrive

first. It must travel a sufficient distance in the

faster layer to compensate for the longer path

(see Problem 17.3). There are corresponding

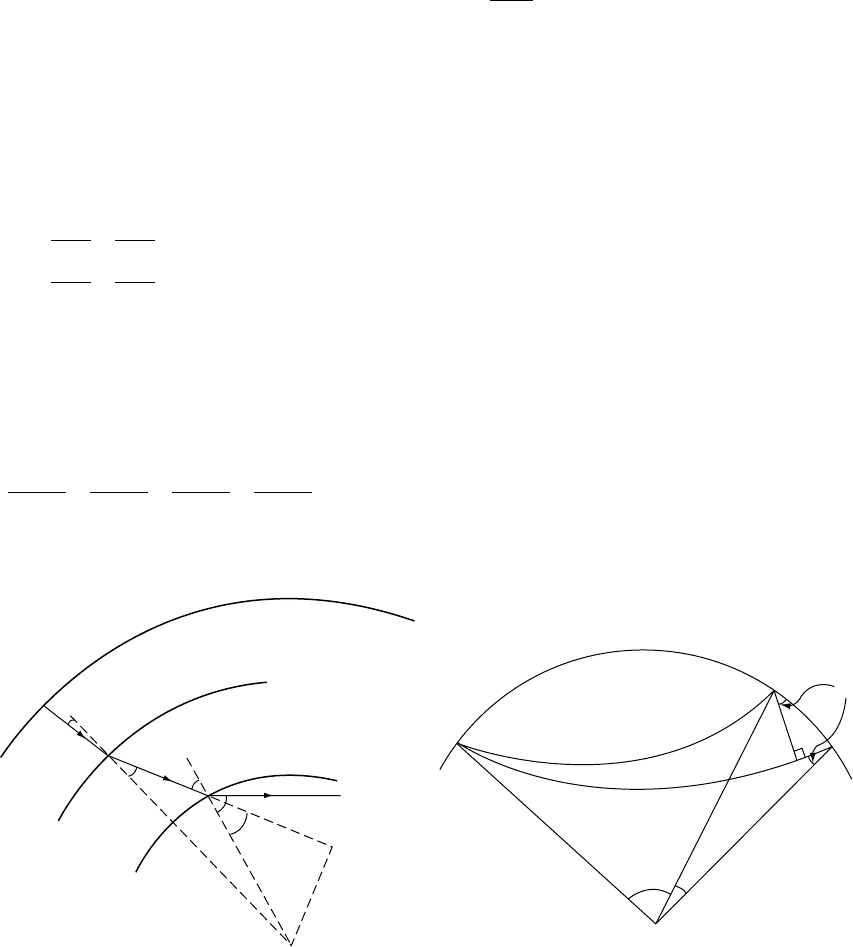
breaks in the travel-time curve with a gradient

change at each point where the faster path

extends to a new layer (Fig. 17.2).

The horizontally layered model is sufficiently

close to the real Earth on a regional scale that a

single line of refraction data can give satisfactory

values of layer thicknesses and speeds. If layers

are inclined, then not only are depths ambiguous

but wave speeds are biased. Consider a layer of

speed V

overlying one with speed V

, and having

an inclined boundary between them, dipping

downwards at angle  away from the source of

seismic waves. The slowness across the surface,

that is, the inverse of surface speed, of a head

wave that travels in the lower medium is

(Problem 17.4)

cos 

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

 V

sin : (17:8)

For small , the first term is little different from

1/V

, as observed with horizontal layers. The sec-

ond term is normally the principal cause of a

biased result. The problem is overcome by mak-

ing measurements of propagation in the oppo-

site direction across the same area. Then the sin 

term is reversed in sign. Both V

and  can be

found with a reversed profile, as when explosive

sources are used in exploration, but the method

has no application to earthquake studies. dS/dT,

from Eq. (17.8), is referred to as the apparent

velocity of the refracted wave along the surface.

If the layer is upward sloping ( negative), for the

case sin  ¼V

, the apparent velocity can be

infinite, with all refracted pulses arrive at the

surface at the same time.

For exploration of the upper crust, much

greater detail is required. This is usually obtained

by using reflections rather than refractions. For

reflection studies sources and receivers are gen-

erally closer together than in refraction work, so

that reflections are obtained close to normal

incidence. Two-way travel times are measured

and this translates into boundary depths when

the layer speeds are known. The travel time of a

reflection from a horizontal layer at depth h as a

function of distance, S,is

T ¼

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

þ S

; (17:9)

which is the equation for a hyperbola. This dis-

tinguishes reflected arrivals from refracted ones

on a travel time (T–S) plot since refracted arrivals

form straight lines (Eq. (17.7)).

ΔT

FI G U R E 17.2 Travel-time curve for first arriving pulses

from a layered structure, as in Fig. 17.1. Numbers on

segments indicate the deepest layer penetrated by each

‘family’ of rays.

270 SEISMOLOGICAL DETERMINATION OF EARTH STRUCTURE

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C17.3D

–

271

– [267–293] 13.3.2008 2:15PM

17.3 Refraction in a spherically

layered Earth

Consider a spherical model of the Earth in which

wave speed, V, varies radially. For the purpose

of the argument that follows it is convenient

to consider a layered model, with each layer uni-

form, but this restriction can be removed by

introducing an infinite number of infinitesimal

layers with a graded wave speed. The geometry

of a seismic ray through a three-layer model is

shown in Fig. 17.3. Applying Snell’s law

(Eq. (16.5)) to each of the boundaries, A and B,

sin i

sin f

sin i

sin f

;

: (17:10)

From the two triangles,

q ¼ r

sin f

¼ r

sin i

; (17:11)

so that if we multiply Eq. (17.9) by r

and Eq. (17.10)

by r

we can then equate them to one another,

sin i

sin f

sin i

sin f

: (17:12)

Equation (17.12) could be extended to any num-

ber of boundaries or to gradual refraction in a

layer of progressively increasing speed. It dem-

onstrates that

r sin i

¼ p (17:13)

is a constant for the ray, where i is the angle

between the ray and the radius at any point. p

is referred to as the ray parameter. It remains

constant not only at refractions and reflections,

but also at wave conversions (P to SV or vice

versa). By determining the parameter of a ray

we obtain the value of r/V at its point of deepest

penetration, where i ¼908.

Now consider two rays from a common sur-

face source with infinitesimally different ray

parameters, as in Fig. 17.4. Their distances of

travel are represented by the angles D and

(D þdD), subtended at the centre of the Earth

by the ends of the ray paths. PN is the normal

from P to SQ and is therefore a wavefront so that

the travel times of paths SP and SN are equal. The

path difference between the rays is therefore QN

and the travel time difference is

dT ¼ QN=V

; (17:14)

where V

is the wave speed in the surface layer.

But

dΔ

FI G U R E 17.4 Two seismic rays with infinitesimally

different distances of travel. This geometrical

construction is used to relate the ray parameter, p, to the

slowness (1/speed) with which wave arrivals cross the

surface. p is the gradient of the travel time curve.

Velocity v

FI G U R E 17.3 Path of a seismic ray through three uniform

layers of a spherical model, showing the geometrical

construction used to prove that the seismic ray

parameter, p ¼r sin i/v, remains constant along the path.

17.3 REFRACTION IN A SPHERICALLY LAYERED EARTH 271

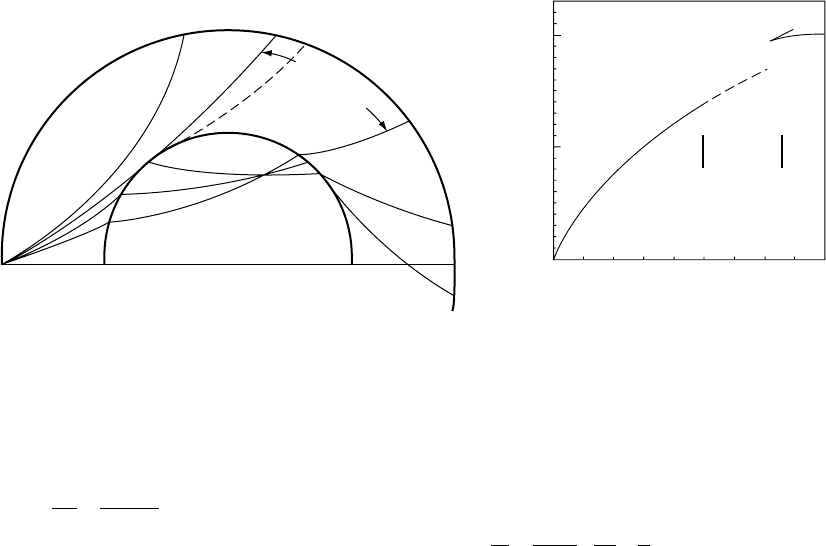
//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C17.3D

–

272

– [267–293] 13.3.2008 2:15PM

QN ¼ PQ sin i

¼ r

d sin i

; (17:15)

so that

d

sin i

¼ p: (17:16)

Thus, a ray parameter is the gradient of the

travel time curve, or slowness, and so can be

directly observed as a function of total angular

distance of travel, D. Linked arrays of seismom-

eters give precise observations of dT/dD and are

particularly useful in investigating complica-

tions, such as occur in the mantle transition

zone.

If wave speed increased gradually inwards

throughout the Earth, then p would progres-

sively decrease with D,andp(D)wouldbeacon-

tinuous, monotonic function. There are large

depth ranges over which this regular behaviour

occurs, giving correspondingly straightforward

p–D and therefore T–D relationships. However,

two effects cause breaks. Whereas an increase

in speed with depth causes rays to turn

upwards, a decrease causes them to turn down-

wards and, if this is more than a slight effect

(corresponding to the curvature of a level sur-

face at that depth), there is a range of depths

over which no rays have their points of deepest

penetration and a break appears in the travel

time curve. The necessary condition for this to

occur may be obtained from Eq. (17.13). Since p

is constant,

p dV

dr ¼ sin i þ r cos i di

dr: (17:17)

Substituting for sin i from Eq. (17.13) and

rearranging,

r cos i





: (17:18)

Thus, the condition to be satisfied to avoid a

decrease in i with depth and a break in the

travel-time curve is dV=dr

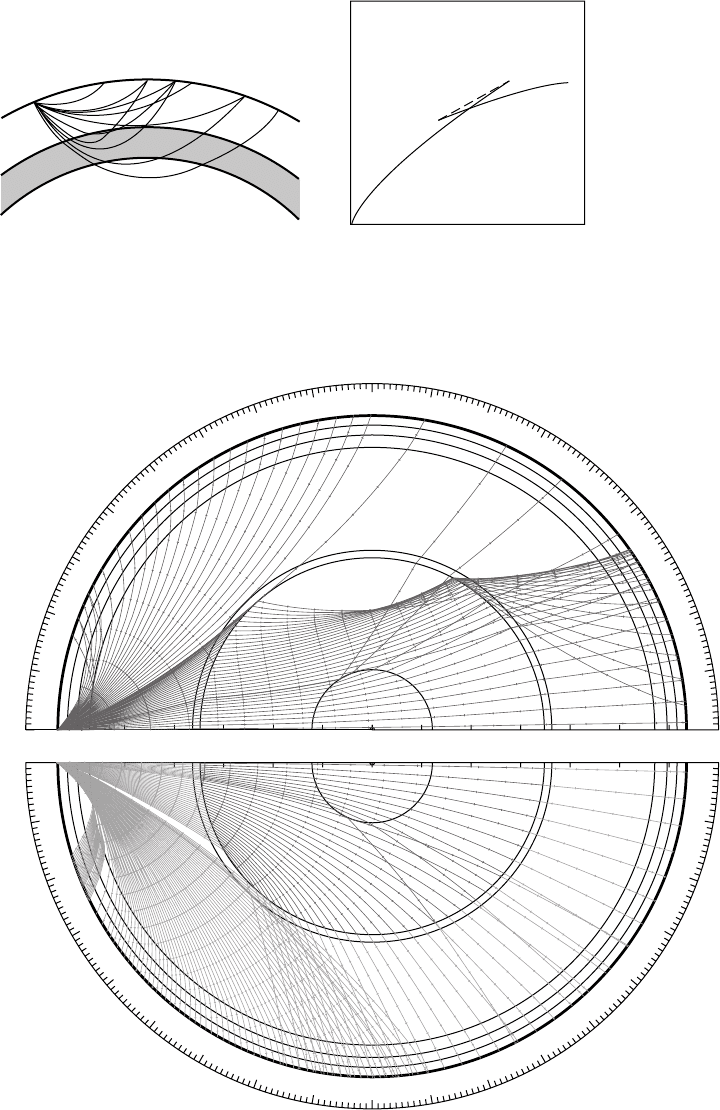
V=r . At the core–

mantle boundary the P-wave speed drops to

less than 60% of its value at the base of the

mantle, causing sharp downward refraction of

P-waves and leading to a shadow zone of dis-

tances over which direct P-waves are not

observed (Fig. 17.5).

A sharp increase in wave speed with depth

causes a complication of a different kind. The

normal trend is an increase in D with increasing

dip angle of the rays, that is, decreasing angle of

incidence, i

. Since p /sin i

, this means that D

increases with decreasing p. But the trend is

reversed by sharp refraction where the rays

enter a steep velocity gradient; the normal

trend is restored with further decrease in p,

that is, increasing steepness of the rays. Such a

velocity increase, although a complicated one,

occurs in the transition zone in the mantle, caus-

ing a range of distances over which three direct P

wave arrivals may be observed (Fig. 17.6). This is

known as triplication.

Diffracted P

PKP

(a)

T (minutes)

20 40 60 80 100 120 140 160 180

Diffracted P

PKP

SHADOW

ZONE

(b)

Δ (degrees)

FI G U R E 17.5 (a) Seismic rays refracted by the core, causing a shadow zone for direct P waves. (b) The

corresponding travel time curve has a break. PKP is the nomenclature of a P wave having part of its path in the core.

272 SEISMOLOGICAL DETERMINATION OF EARTH STRUCTURE

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C17.3D

–

273

– [267–293] 13.3.2008 2:15PM

FI G U RE 17.6 A zone in which

velocity increases sharply with

depth causes reversal of the p–D

trend and a range of distances

over which arrivals are triplicated.

A point such as P may receive

three rays, each one on a different

limb of the T D curve. This figure

is illustrative and not to scale.

10.

20.

30.

40.

50.

60.

70.

80.

90.

100.

110.

120.

130.

140.

150.

160.

170.

180.

1000.

2000.

3000.

4000.

5000.

6000.

7000.

PKP

PKIKP

PKiKP

SKIKS

SKS

SKiKS

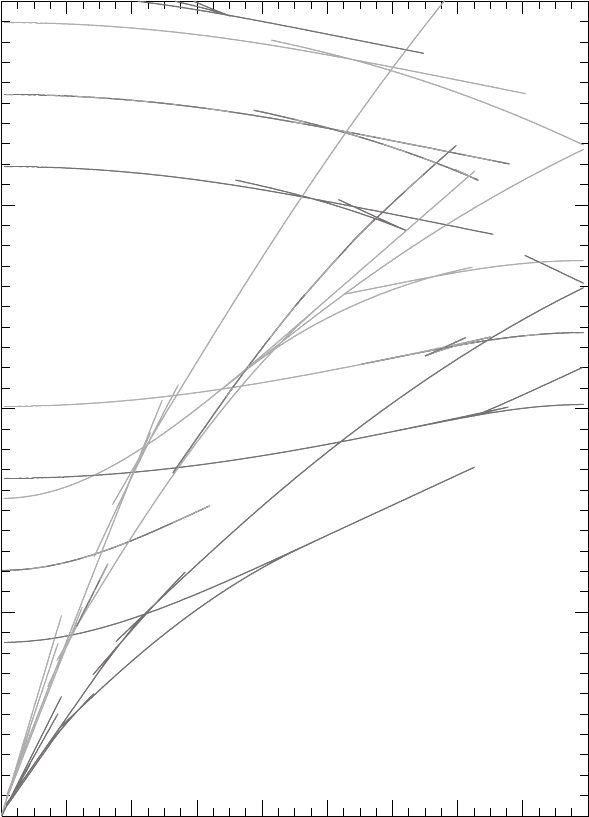
FI G U R E 17.7 Paths of seismic rays through the Earth, illustrating their nomenclature. Figure by courtesy of

B. L. N. Kennett.

17.3 REFRACTION IN A SPHERICALLY LAYERED EARTH 273

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C17.3D

–

274

– [267–293] 13.3.2008 2:15PM

17.4 Travel times and the velocity

distribution

Complications in the structure of the Earth men-

tioned above cause a multiplicity of wave paths,

many of which have well observed travel times

and are useful in determining details of the struc-

ture. Fig. 17.7 identifies some of these, with let-

ters P and S referring to waves in the mantle. For

sources below the surface, waves are also

received from surface reflections and in these

cases an initial p or s is applied to the designa-

tion, e.g., pP, sS. K indicates a P-wave in the outer

20. 40. 60. 80. 100. 120. 140. 160. 180.

Delta [de

]

10.

20.

30.

40.

Time [min]

PKKS

PKKP

SKiKP

ScP

PcP

P'P'

SKKS

PKiKP

SKKS

Sdiff

SKS

SKP

PKP

Pdiff

ScS

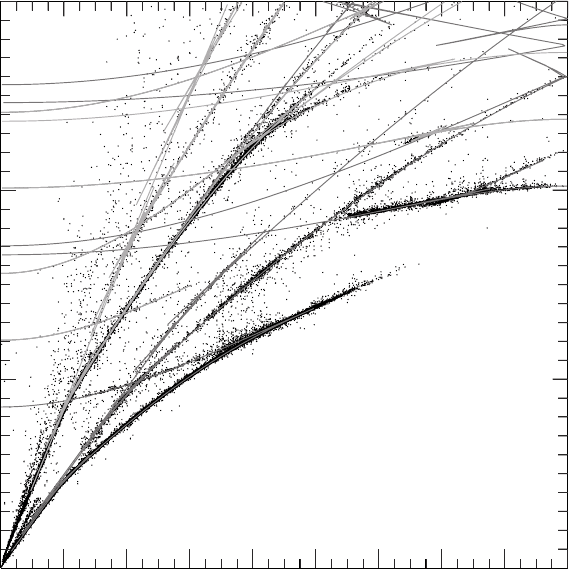
FI G U R E 17.8 (a) Graph of travel times of seismic phases identified in the IASPEI 1991 Seismological Tables.

Reproduced by permission from Kennett and Engdahl (1991). (b) The lower part of Fig. 17.8(a) with travel times from

the Bulletin of the International Seismological Centre (ISC). Courtesy of B. L. N. Kennett.

274 SEISMOLOGICAL DETERMINATION OF EARTH STRUCTURE

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C17.3D

–

275

– [267–293] 13.3.2008 2:15PM

core (German Kern or kernel), where there are

no S-waves, and I refers to a P-wave in the solid

inner core. The letter J is reserved for shear

waves in the inner core. Although shear waves

would be expected for a solid, observations

are marginal (Section 16.6). Excitation of J

phases requires conversion from P- to S-waves

on entry to the inner core and conversion back

to P-waves on re-emergence into the outer core,

and these conversions are very weak. As at the

surface, lower case letters indicate reflections.

Occasionally numbers appear in the nomencla-

ture. These give either the depth in kilometres at

which reflections occur, or the multiplicity of

internal reflections, especially at the core–mantle

boundary.

For many years the tables of travel times pub-

lished in 1940 by H. Jeffreys and K. E. Bullen, and

known as the J-B tables, were the reference

standard. Improvements in certain details have

appeared from time to time, particularly direct P-

and S-wave times, but there is now an updated

comprehensive set of tables (Kennett et al., 1995;

wwwrses.anu.edu.au/seismology/ak135), illus-

trated in Fig. 17.8. This model, ak135, is based

on an earlier model (iasp91) (Kennett and

Engdahl, 1991; Montagner and Kennett 1996).

The tables give times for numerous phases, as a

mutually consistent set, obtained by adjusting

a velocity model (Fig. 17.9) to give a best fit to a

large number of observed travel times. Further

important developments in modelling the velo-

city structure have begun to appear with the use

of records from a global digital seismograph net-

work. The records can be ‘stacked’, that is, added

together numerically, to enhance signals, with

cancellation of noise that is not coherent on the

multiple records that are added. Shearer (1990)

40. 60. 80. 100. 120. 140. 160.

10.

20.

30.

Time [min]

20. 180.

Δ [deg]

PcP

ScP

ScS

PPP

SSS

PKP

SKP

SKS

SKKS

FI G U R E 17.8 (Cont.)

17.4 TRAVEL TIMES AND THE VELOCITY DISTRIBUTION 275

//FS2/CUP/3-PAGINATION/SDE/2-PROOFS/3B2/9780521873628C17.3D

–

276

– [267–293] 13.3.2008 2:15PM

has applied this method to reflected waves from

the upper mantle.

To see how travel times are used to deduce

the Earth’s velocity structure, consider the

geometry of Fig. 17.10. A short element ds in

the path of a ray makes an angle i to the radius

at that point, so the contribution to D by that

element is d, where

r d ¼ sin i ds: (17:19)

Using this relationship to substitute for sin i in

the expression for p (Eq. (17.13)),

p ¼

r sin i

rd

: (17:20)

But the small elementary triangle in Fig. 17.10

gives also

dsðÞ

¼ drðÞ

þ rdðÞ

; (17:21)

and we can eliminate ds from Eqs. (17.20) and

(17.21),

d



¼ dr

þ r dðÞ

: (17:22)

With the introduction of a parameter  ¼r/V,we

obtain

1000 2000 30000 4000 5000 6000 6371

Depth (km)

(km s

–1

)

FI G U R E 17.9 P- and S-wave speeds, V

and V

, in the ak135 model of the Earth developed from body wave travel times

(Kennett et al., 1995). Details of the model can be found at wwwrses.anu.edu.au/seismology/ak135.

d θ = ds.sini

dθ

FI G U R E 17.10 Geometry used

to obtain an integral expression

for travel distance D in terms of

seismic ray parameter, p.

276 SEISMOLOGICAL DETERMINATION OF EARTH STRUCTURE