Stewart J. Calculus

Подождите немного. Документ загружается.

282

|| ||

CHAPTER 4 APPLICATIONS OF DIFFERENTIATION

Determine whether the statement is true or false. If it is true, explain why.

If it is false, explain why or give an example that disproves the statement.

1. If , then has a local maximum or minimum at .

2. If has an absolute minimum value at , then .

3. If is continuous on , then attains an absolute maxi-

mum value and an absolute minimum value at some

numbers and in .

4. If is differentiable and , then there is a number

such that and .

5. If for , then is decreasing on (1, 6).

6. If , then is an inﬂection point of the

curve .

7. If for , then for

8. There exists a function such that , and

for all .

9. There exists a function such that , , and

for all .

10. There exists a function such that

, ,

and for all .xf ) "x# ' 0

f %"x#

0f "x#

xf ) "x# ' 0

f %"x#

0f "x# ' 0f

xf %"x# ' 1

f "1# ! "2, f "3# ! 0f

f "x# ! t"x#

f %"x# ! t%"x#

y !

f "x#

"2, f "2##f )"2# ! 0

f %"x#

f %"c# ! 0

f ""1# ! f "1#f

"a, b#dc

f "d #f "c#

f"a, b#f

f %"c# ! 0cf

cff %"c# ! 0

11. If and are increasing on an interval , then is

increasing on .

12. If and are increasing on an interval , then is

increasing on .

13. If and are increasing on an interval , then is increasing

on .

14. If and are positive increasing functions on an interval ,

then is increasing on .

15. If is increasing and on , then is

decreasing on .

16. If is even, then is even.

17. If is periodic, then is periodic.

18. The most general antiderivative of is

19. If exists and is nonzero for all , then .f "1# " f "0#xf %"x#

F"x# ! "

# C

f "x# ! x

f %f

t"x# ! 1$f "x#If "x# ' 0f

Ift

Itf

ftItf

f " tItf

f # tItf

T R U E - FA L S E Q U I Z

13–15 Sketch the graph of a function that satisﬁes the given

conditions:

13. ,

on , and

on and

14. , is continuous and even,

if if ,

15. is odd, for ,

for , for ,

for ,

16. The ﬁgure shows the graph of the derivative of a function .

(a) On what intervals is increasing or decreasing?

(b) For what values of does have a local maximum or

minimum?

ff %

lim

x l *

f "x# ! "2x ' 3

f )"x#

f )"x# ' 0x ' 2f %"x# ' 0

2f %"x#

x ' 3f %"x# ! 1

1, f %"x# ! "1

f %"x# ! 2x

ff "0# ! 0

"6, 12#"0, 6

f )"x#

"12, *#,""*, 0#f )"x# ' 0

"6, 9#,""2, 1#f %"x# ' 0

"9, *#,""*, "2#, "1, 6#

f %"x#

lim

f "x# ! 0, lim

f "x# ! "*,

f "0# ! 0, f %""2# ! f %"1# ! f %"9# ! 0

1–6 Find the local and absolute extreme values of the function on

the given interval.

1. ,

2. ,

3. ,

4. ,

5. ,

6. ,

7–12 Find the limit.

7. 8.

9. 10.

11. 12.

lim

sin

lim

(

# 3x

" 2x

)

lim

# x

#lim

# 1

3x " 1

lim

" t # 2

"2t " 1#"t

# t # 1#

lim

# x " 5

" 2x

# 1

%0,

&f "x# ! sin x # cos

%0,

&f "x# ! x # sin 2x

%"2, 1&f "x# ! "x

# 2x#

%"2, 2&f "x# !

3x " 4

# 1

%"1, 1&f "x# ! x

1 " x

%2, 4&f "x# ! x

" 6x

# 9x # 1

E X E R C I S E S

CHAPTER 4 REVIEW

|| ||

283

38. Find two positive integers such that the sum of the ﬁrst num-

ber and four times the second number is 1000 and the product

of the numbers is as large as possible.

39. Show that the shortest distance from the point to the

straight line is

40. Find the point on the hyperbola that is closest to the

point .

41. Find the smallest possible area of an isosceles triangle that is

circumscribed about a circle of radius .

42. Find the volume of the largest circular cone that can be

inscribed in a sphere of radius .

43. In , lies on , , cm,

and cm. Where should a point be chosen on

so that the sum is a minimum?

44. Solve Exercise 43 when cm.

45. The velocity of a wave of length in deep water is

where and are known positive constants. What is the

length of the wave that gives the minimum velocity?

46. A metal storage tank with volume is to be constructed in

the shape of a right circular cylinder surmounted by a hemi-

sphere. What dimensions will require the least amount of

metal?

47. A hockey team plays in an arena with a seating capacity of

15,000 spectators. With the ticket price set at , average

attendance at a game has been 11,000. A market survey indi-

cates that for each dollar the ticket price is lowered, average

attendance will increase by 1000. How should the owners of

the team set the ticket price to maximize their revenue from

ticket sales?

;

48. A manufacturer determines that the cost of making units of

a commodity is and

the demand function is .

(a) Graph the cost and revenue functions and use the graphs

to estimate the production level for maximum proﬁt.

(b) Use calculus to ﬁnd the production level for maximum

proﬁt.

cost.

49. Use Newton’s method to ﬁnd the root of the equation

in the interval correct to

six decimal places.

50. Use Newton’s method to ﬁnd all roots of the equation

correct to six decimal places.sin x ! x

" 3x # 1

%1, 2&x

" x

# 3x

" 3x " 2 ! 0

p"x# ! 48.2 " 0.03x

C"x# ! 1800 # 25x " 0.2x

# 0.001x

$12

v ! K

! 2

CDP

! 5

! 4CD ! ABABD0ABC

"3, 0#

xy ! 8

# By

# C

# B

Ax # By # C ! 0

, y

(d) Sketch a possible graph of .

17–28 Use the guidelines of Section 4.5 to sketch the curve.

17. 18.

19. 20.

21. 22.

23. 24.

25. 26.

27.

28.

;

29–32 Produce graphs of that reveal all the important aspects

of the curve. Use graphs of and to estimate the intervals of

increase and decrease, extreme values, intervals of concavity, and

inﬂection points. In Exercise 29 use calculus to ﬁnd these quanti-

ties exactly.

29. 30.

31.

32.

33. Show that the equation has exactly one

real root.

34. Suppose that is continuous on , and

for all in . Show that .

35. By applying the Mean Value Theorem to the function

on the interval , show that

36. For what values of the constants and is a point of

inﬂection of the curve ?

37. Let , where is twice differentiable for all ,

for all , and is concave downward on

and concave upward on .

(a) At what numbers does have an extreme value?

(b) Discuss the concavity of .t

"0, *#""*, 0#

fx " 0f %"x# ' 0

xft"x# ! f "x

y ! x

# ax

# bx # 1

"1, 6#ba

2.0125

%32, 33&f "x# ! x

1$5

9 / f "4# / 21"0, 4#x2 / f %"x# / 5

%0, 4&, f "0# ! 1f

3x # 2 cos x # 5 ! 0

f "x# ! x

# 6.5 sin x, "5 / x / 5

f "x# ! 3x

" 5x

# x

" 5x

" 2x

# 2

f "x# !

" x

# x # 3

f "x# !

" 1

f )f %

y ! 4x " tan x, "

y ! sin

x " 2 cos x

y !

# 1

y ! x

2 # x

y !

1 " x

1 # x

y ! x

$"x # 8#

y !

"x " 2#

y !

x"x " 3#

y !

1 " x

y ! x

" 3x

# 3x

" x

y ! x

" 6x

" 15x # 4y ! 2 " 2x " x

1 2 3 4 5 6 7

y=f ª(x)

f )

284

|| ||

CHAPTER 4 APPLICATIONS OF DIFFERENTIATION

65. A rectangular beam will be cut from a cylindrical log of

radius 10 inches.

(a) Show that the beam of maximal cross-sectional area is

a square.

(b) Four rectangular planks will be cut from the four sections

of the log that remain after cutting the square beam. Deter-

mine the dimensions of the planks that will have maximal

cross-sectional area.

tional to the product of its width and the square of its

depth. Find the dimensions of the strongest beam that can

be cut from the cylindrical log.

66. If a projectile is ﬁred with an initial velocity at an angle of

inclination from the horizontal, then its trajectory, neglect-

ing air resistance, is the parabola

(a) Suppose the projectile is ﬁred from the base of a plane

that is inclined at an angle , , from the horizontal,

as shown in the ﬁgure. Show that the range of the projec-

tile, measured up the slope, is given by

(b) Determine so that is a maximum.

Determine the range in this case, and determine the

angle at which the projectile should be ﬁred to maximize .

" !

cos

sin!

t cos

$ 0

0 %

y ! !tan

"x #

cos

depth

width

51. Use Newton’s method to ﬁnd the absolute maximum value of

the function correct to eight decimal

places.

52. Use the guidelines in Section 4.5 to sketch the curve

, . Use Newton’s method when

necessary.

53–58 Find .

53.

54.

55.

56. ,

57. , ,

58. , ,

59–60 A particle is moving with the given data. Find the position

of the particle.

59. ,

60. , ,

;

61. Use a graphing device to draw a graph of the function

, , and use that graph to sketch

the antiderivative of that satisﬁes the initial condition

;

62. Investigate the family of curves given by

In particular you should determine the transitional value of

at which the number of critical numbers changes and the

transitional value at which the number of inﬂection points

changes. Illustrate the various possible shapes with graphs.

63. A canister is dropped from a helicopter m above the

ground. Its parachute does not open, but the canister has been

designed to withstand an impact velocity of m#s. Will it

burst?

64. In an automobile race along a straight road, car A passed

car B twice. Prove that at some time during the race their

accelerations were equal. State the assumptions that you

make.

100

500

f !x" ! x

' x

' cx

F!0" ! 0

0 % x %

f !x" ! x

sin!x

v!0" ! 2s!0" ! 0a!t" ! sin t ' 3 cos t

s!0" ! 3

v!t" ! 2t # sin t

f !1" ! 0f !0" ! 2f (!x" ! 2x

' 3x

# 4x ' 5

f )!0" ! 2f !0" ! 1f (!x" ! 1 # 6x ' 48x

f !1" ! 3f )!u" !

f !0" ! 5f )!t" ! 2t # 3 sin t

f )!x" ! 8x # 3 sec

f )!x" !

0 % x % 2

y ! x sin x

f !t" ! cos t ' t # t

285

One of the most important principles of problem solving is analogy (see page 54). If you

are having trouble getting started on a problem, it is sometimes helpful to start by solving

a similar, but simpler, problem. The following example illustrates the principle. Cover up

the solution and try solving it yourself ﬁrst.

EXAMPLE 1 If x, y, and are positive numbers, prove that

SOLUTION It may be difﬁcult to get started on this problem. (Some students have tackled

it by multiplying out the numerator, but that just creates a mess.) Let’s try to think of a

similar, simpler problem. When several variables are involved, it’s often helpful to think

of an analogous problem with fewer variables. In the present case we can reduce the

number of variables from three to one and prove the analogous inequality

In fact, if we are able to prove (1), then the desired inequality follows because

The key to proving (1) is to recognize that it is a disguised version of a minimum prob-

lem. If we let

then , so when x ! 1. Also, for and

for . Therefore the absolute minimum value of is . This means

that

for all positive values of x

and, as previously mentioned, the given inequality follows by multiplication.

The inequality in (1) could also be proved without calculus. In fact, if , we have

Because the last inequality is obviously true, the ﬁrst one is true too. M

&? !x # 1"

* 0

' 1

* 2 &? x

' 1 * 2x &? x

# 2x ' 1 * 0

x $ 0

' 1

* 2

f !1" ! 2fx $ 1f )!x" $ 0

1f )!x"

0f )!x" ! 0f )!x" ! 1 # !1#x

x $ 0f !x" !

' 1

! x '

' 1"!y

' 1"!z

' 1"

xyz

' 1

* 2 ! 2 ! 2 ! 8

' 1

* 2 for x $ 0

' 1"!y

' 1"!z

' 1"

xyz

* 8

P R O B L E M S P L U S

Look Back

What have we learned from the solution to this

example?

N To solve a problem involving several variables,

it might help to solve a similar problem with

just one variable.

N When trying to prove an inequality, it might

help to think of it as a maximum or minimum

problem.

286

1. Show that for all .

2. Show that for all numbers and such that and .

3. Let and be positive numbers. Show that not both of the numbers and

can be greater than .

4. Find the point on the parabola at which the tangent line cuts from the ﬁrst quad-

rant the triangle with the smallest area.

5. Find the highest and lowest points on the curve .

6. Water is ﬂowing at a constant rate into a spherical tank. Let be the volume of water in the

tank and be the height of the water in the tank at time .

(a) What are the meanings of and ? Are these derivatives positive, negative, or

zero?

(b) Is positive, negative, or zero? Explain.

full, respectively. Are the values , , and positive, negative, or zero? Why?

7. Find the absolute maximum value of the function

8. Find a function such that and for all , or prove that such

a function cannot exist.

9. The line intersects the parabola in points and . (See the ﬁgure.) Find

the point on the arc of the parabola that maximizes the area of the triangle .

10. Sketch the graph of a function such that for all for

for , and .

11. Determine the values of the number for which the function has no critical number:

12. Sketch the region in the plane consisting of all points such that

13. Let be a triangle with and .

(a) Express the length of the angle bisector in terms of .

(b) Find the largest possible value of .

14. (a) Let be a triangle with right angle and hypotenuse . (See the ﬁgure.) If

the inscribed circle touches the hypotenuse at , show that

(b) If , express the radius of the inscribed circle in terms of and .

15. A triangle with sides , and varies with time , but its area never changes. Let be the

angle opposite the side of length and suppose always remains acute.

(a) Express in terms of , , , , and .

(b) Express in terms of the quantities in part (a).da#dt

dc#dtdb#dt

cbd

#dt

tca, b

(

)

a !

AABC

x !

! 1!BAC ! 120,ABC

2xy %

x # y

% x

' y

!x, y"

f !x" ! !a

' a # 6" cos 2x ' !a # 2"x ' cos 1

lim

x l-.

' f !x" ' x( ! 0

f (!x"

$ 1,x, f (!x" $ 0f )!x"

PABAOBP

BAy ! x

y ! mx ' b

xf (!x" $ 0f )!#1" !

, f )!0" ! 0,f

f !x" !

1 '

x # 2

H(!t

"H (!t

"H(!t

V (!t"

H)!t"V)!t"

tH!t"

V!t"

' x y ' y

! 12

y ! 1 # x

b!1 # a"a!1 # b"ba

% 2

% 2yxx

!4 # x

"!4 # y

" % 16

sin x # cos x

PROBLEM S

P R O B L E M S P L U S

F I G U R E F O R P RO B LE M 9

y=≈

y=mx+b

F I G U R E F O R P RO B LE M 1 4

287

16. is a square piece of paper with sides of length 1 m. A quarter-circle is drawn from to

with center . The piece of paper is folded along , with on and on , so that

falls on the quarter-circle. Determine the maximum and minimum areas that the triangle

can have.

17. The speeds of sound in an upper layer and in a lower layer of rock and the thickness of

the upper layer can be determined by seismic exploration if the speed of sound in the lower

layer is greater than the speed in the upper layer. A dynamite charge is detonated at a point

and the transmitted signals are recorded at a point , which is a distance from . The ﬁrst

signal to arrive at travels along the surface and takes seconds. The next signal travels

from to a point , from to in the lower layer, and then to taking seconds. The third

signal is reﬂected off the lower layer at the midpoint of and takes seconds to reach .

(a) Express in terms of .

(b) Show that is a minimum when .

Note: Geophysicists use this technique when studying the structure of the earth’s crust,

whether searching for oil or examining fault lines.

18. For what values of is there a straight line that intersects the curve

in four distinct points?

19. One of the problems posed by the Marquis de l’Hospital in his calculus textbook Analyse des

Inﬁniment Petits concerns a pulley that is attached to the ceiling of a room at a point by a

rope of length . At another point on the ceiling, at a distance from (where ), a

rope of length ! is attached and passed through the pulley at and connected to a weight .

The weight is released and comes to rest at its equilibrium position . As l’Hospital argued,

this happens when the distance is maximized. Show that when the system reaches equi-

librium, the value of is

Notice that this expression is independent of both and !.

20. Given a sphere with radius , ﬁnd the height of a pyramid of minimum volume whose base is

a square and whose base and triangular faces are all tangent to the sphere. What if the base of

the pyramid is a regular -gon? (A regular -gon is a polygon with equal sides and angles.)

(Use the fact that the volume of a pyramid is , where is the area of the base.)

21. Assume that a snowball melts so that its volume decreases at a rate proportional to its surface

area. If it takes three hours for the snowball to decrease to half its original volume, how much

longer will it take for the snowball to melt completely?

22. A hemispherical bubble is placed on a spherical bubble of radius 1. A smaller hemispherical

bubble is then placed on the ﬁrst one. This process is continued until chambers, including

the sphere, are formed. (The ﬁgure shows the case .) Use mathematical induction to

prove that the maximum height of any bubble tower with chambers is .1 '

n ! 4

nnn

(

r '

' 8d

)

d $ rCdBr

y ! x

' cx

' 12x

# 5x ' 2

Speed of sound=c™

Speed of sound=c¡

, c

, and hT

! 0.34 sT

! 0.32 sT

! 0.26 sD ! 1 km

sin

! c

D, h, c

, c

, and

, T

, and T

RSO

Q,SRRP

PDQ

AEF

AADFABEEFAD

BABCD

P R O B L E M S P L U S

F I G U R E F O R P R O B L E M 1 9

B E

F I G U R E F O R P R O B L E M 2 2

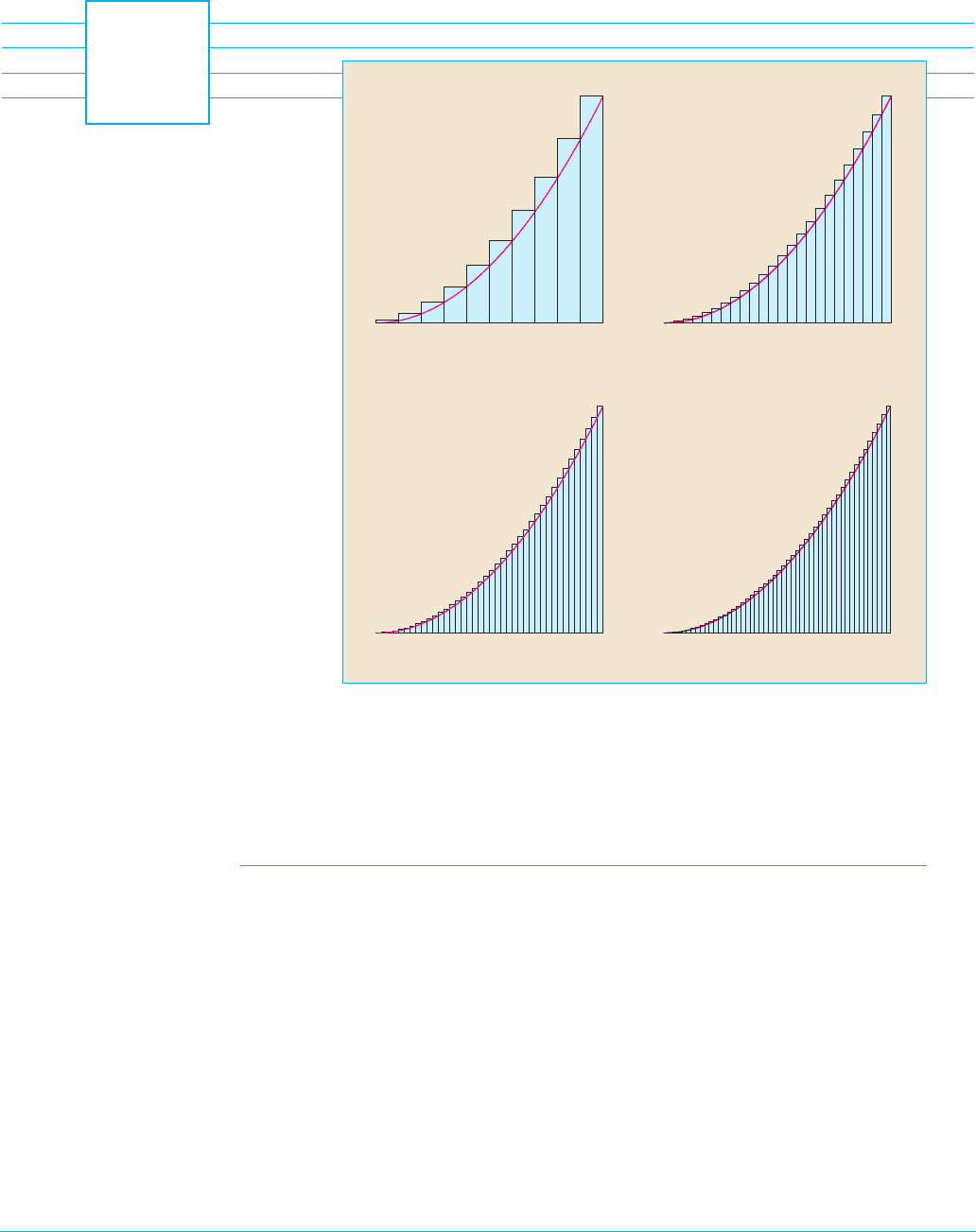
288

In Chapter 3 we used the tangent and velocity problems to introduce the derivative,

which is the central idea in differential calculus. In much the same way, this chapter

starts with the area and distance problems and uses them to formulate the idea of a

deﬁnite integral, which is the basic concept of integral calculus. We will see in

Chapters 6 and 9 how to use the integral to solve problems concerning volumes, lengths

of curves, population predictions, cardiac output, forces on a dam, work, consumer

surplus, and baseball, among many others.

There is a connection between integral calculus and differential calculus. The Funda-

mental Theorem of Calculus relates the integral to the derivative, and we will see in this

chapter that it greatly simpliﬁes the solution of many problems.

To compute an area we approximate a region by rectangles

and let the number of rectangles become large.The precise

area is the limit of these sums of areas of rectangles.

INTEGRALS

AREAS AND DISTANCES

In this section we discover that in trying to ﬁnd the area under a curve or the distance

traveled by a car, we end up with the same special type of limit.

THE AREA PROBLEM

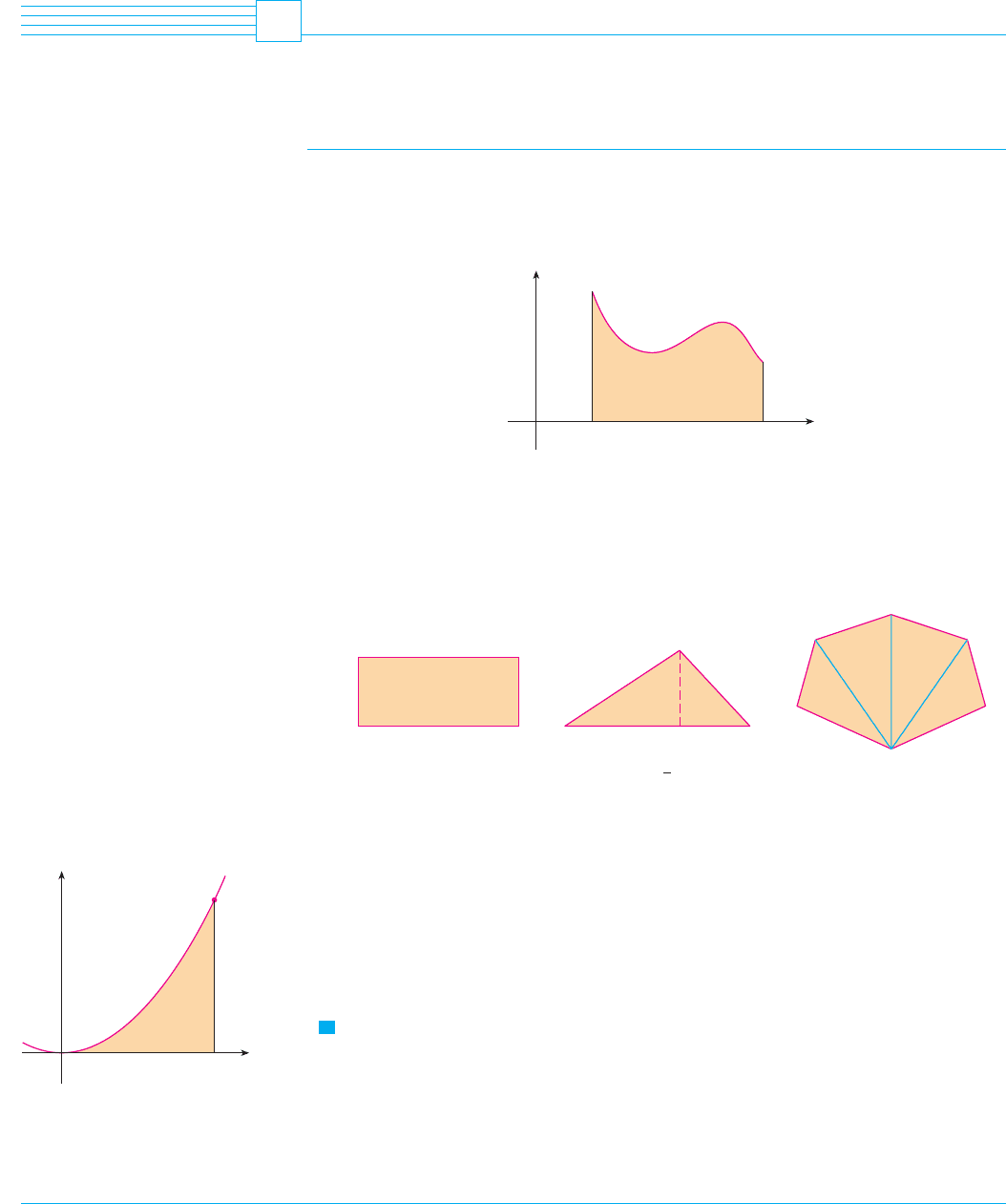
We begin by attempting to solve the area problem: Find the area of the region that lies

under the curve from to . This means that , illustrated in Figure 1, is bounded

by the graph of a continuous function [where ], the vertical lines and

, and the -axis.

In trying to solve the area problem we have to ask ourselves: What is the meaning of

the word area? This question is easy to answer for regions with straight sides. For a rect-

angle, the area is deﬁned as the product of the length and the width. The area of a triangle

is half the base times the height. The area of a polygon is found by dividing it into tri-

angles (as in Figure 2) and adding the areas of the triangles.

However, it isn’t so easy to ﬁnd the area of a region with curved sides. We all have an

intuitive idea of what the area of a region is. But part of the area problem is to make this

intuitive idea precise by giving an exact deﬁnition of area.

Recall that in deﬁning a tangent we ﬁrst approximated the slope of the tangent line by

slopes of secant lines and then we took the limit of these approximations. We pursue a sim-

ilar idea for areas. We ﬁrst approximate the region by rectangles and then we take the

limit of the areas of these rectangles as we increase the number of rectangles. The follow-

ing example illustrates the procedure.

EXAMPLE 1 Use rectangles to estimate the area under the parabola from 0 to 1

(the parabolic region S illustrated in Figure 3).

SOLUTION We ﬁrst notice that the area of S must be somewhere between 0 and 1 because

is contained in a square with side length 1, but we can certainly do better than that. S

y ! x

F I G U R E 2

A= bh

A¡

A™

A£

A¢

A=A¡+A™+A£+A¢

A=lw

a b

y=ƒ

x=a

x=b

F I G U R E 1

S=s(x,y)|a¯x¯b, 0¯y¯ƒd

xx ! b

x ! af !x" ! 0f

Sbay ! f !x"

5.1

289

N Now is a good time to read (or reread)

A Preview of Calculus

(see page 2). It discusses

the unifying ideas of calculus and helps put in

perspective where we have been and where we

are going.

F I G U R E 3

(1,1)

y=≈

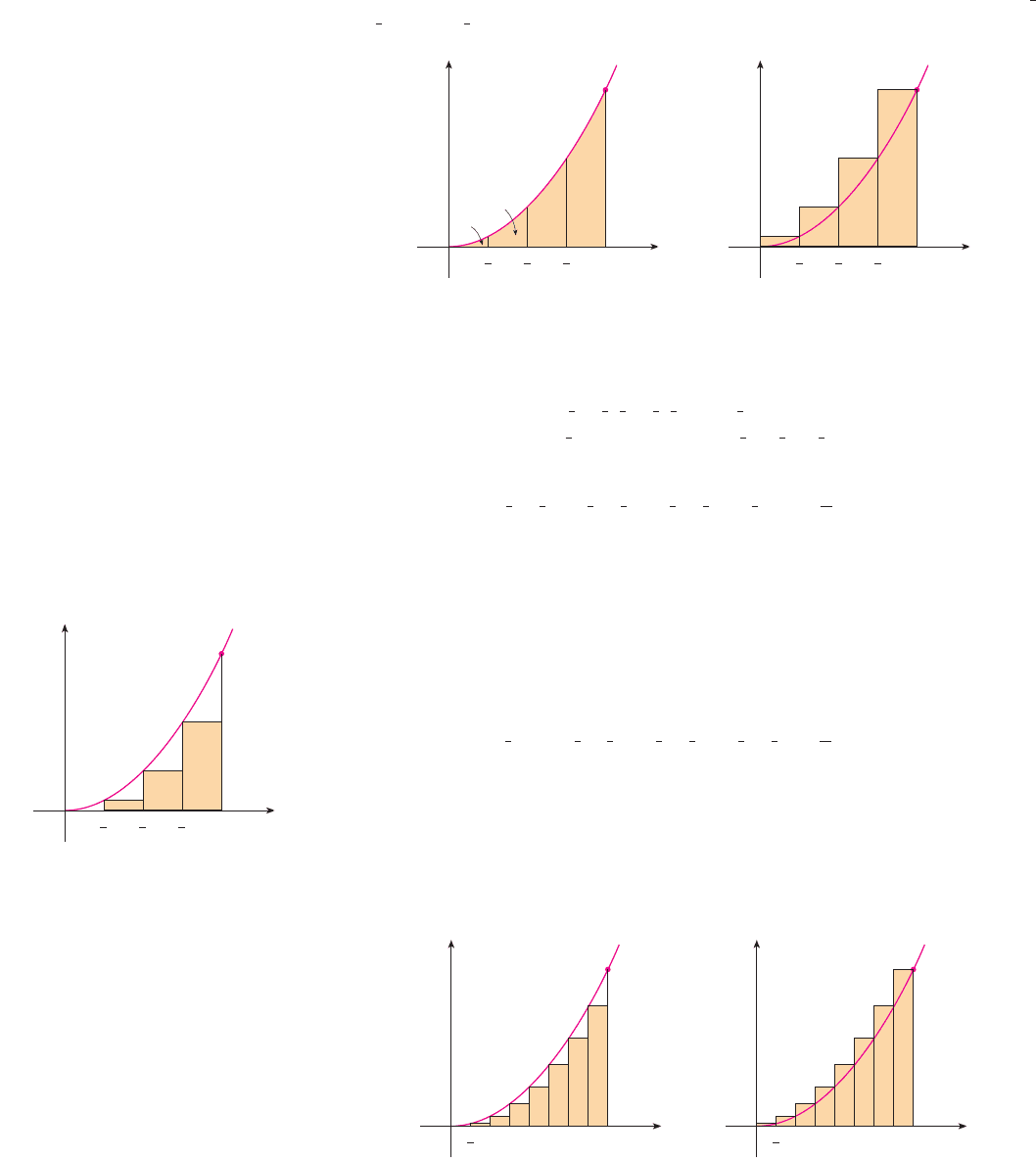
Suppose we divide S into four strips , , , and by drawing the vertical lines ,

, and as in Figure 4(a).

We can approximate each strip by a rectangle whose base is the same as the strip and

whose height is the same as the right edge of the strip [see Figure 4(b)]. In other words,

the heights of these rectangles are the values of the function at the right end-

points of the subintervals , , , and .

Each rectangle has width and the heights are , , , and . If we let be

the sum of the areas of these approximating rectangles, we get

From Figure 4(b) we see that the area A of S is less than , so

Instead of using the rectangles in Figure 4(b) we could use the smaller rectangles in

Figure 5 whose heights are the values of at the left endpoints of the subintervals. (The

leftmost rectangle has collapsed because its height is 0.) The sum of the areas of these

approximating rectangles is

We see that the area of S is larger than , so we have lower and upper estimates for A:

We can repeat this procedure with a larger number of strips. Figure 6 shows what

happens when we divide the region S into eight strips of equal width.

F I G U R E 6

Approximating S with eight rectangles

(a) Using left endpoints (b) Using right endpoints

(1,1)

y=≈

(1,1)

0.21875

0.46875

! 0

(

)

(

)

(

)

! 0.21875

0.46875

(

)

(

)

(

)

! 1

! 0.46875

(

)

(

)

(

)

[

, 1

][

]

f !x" ! x

F I G U R E 4

(b)

(1,1)

(a)

(1,1)

y=≈

S¢

S£

S™

S¡

x !

290

|| ||

CHAPTER 5 INTEGRALS

(1,1)

y=≈

F I G U R E 5

By computing the sum of the areas of the smaller rectangles and the sum of the

areas of the larger rectangles , we obtain better lower and upper estimates for A:

So one possible answer to the question is to say that the true area of S lies somewhere

between 0.2734375 and 0.3984375.

We could obtain better estimates by increasing the number of strips. The table at the

left shows the results of similar calculations (with a computer) using n rectangles whose

heights are found with left endpoints or right endpoints . In particular, we see

by using 50 strips that the area lies between 0.3234 and 0.3434. With 1000 strips we

narrow it down even more: A lies between 0.3328335 and 0.3338335. A good estimate is

obtained by averaging these numbers: . M

From the values in the table in Example 1, it looks as if is approaching as n

increases. We conﬁrm this in the next example.

EXAMPLE 2 For the region S in Example 1, show that the sum of the areas of the

upper approximating rectangles approaches , that is,

SOLUTION is the sum of the areas of the rectangles in Figure 7. Each rectangle

has width and the heights are the values of the function at the points

; that is, the heights are . Thus

Here we need the formula for the sum of the squares of the ﬁrst n positive integers:

Perhaps you have seen this formula before. It is proved in Example 5 in Appendix E.

Putting Formula 1 into our expression for , we get

Thus we have

! 1 ! 2 !

! lim

1 #

2 #

! lim

n # 1

2n # 1

lim

! lim

!n # 1"!2n # 1"

n!n # 1"!2n # 1"

!n # 1"!2n # 1"

# 2

# 3

# % % % # n

n!n # 1"!2n # 1"

# 2

# 3

# % % % # n

# 2

# 3

# % % % # n

# % % % #

!1%n"

, !2%n"

, !3%n"

, . . . , !n%n"

1%n, 2%n, 3%n, . . . , n%n

f !x" ! x

1%n

lim

n l $

A & 0.3333335

"!L

0.2734375

0.3984375

SECTION 5.1 AREAS AND DISTANCES

|| ||

291

10 0.2850000 0.3850000

20 0.3087500 0.3587500

30 0.3168519 0.3501852

50 0.3234000 0.3434000

100 0.3283500 0.3383500

1000 0.3328335 0.3338335

F I G U R E 7

(1,1)

y=≈

N Here we are computing the limit of the

sequence . Sequences were discussed in

A Preview of Calculus

and will be studied in

detail in Chapter 12. Their limits are calculated in

the same way as limits at inﬁnity (Section 4.4). In

particular, we know that

lim

n l $

! 0

(