Stewart J. Calculus

If the subinterval widths are , we have to ensure that all these widths

approach 0 in the limiting process. This happens if the largest width, , approaches

0. So in this case the deﬁnition of a deﬁnite integral becomes

We have deﬁned the deﬁnite integral for an inegrable function, but not all func-

tions are integrable (see Exercises 67– 68). The following theorem shows that the most

commonly occurring functions are in fact integrable. It is proved in more advanced courses.

THEOREM If is continuous on , or if has only a ﬁnite number of

jump discontinuities, then is integrable on ; that is, the deﬁnite integral

exists.

If is integrable on , then the limit in Deﬁnition 2 exists and gives the same value

no matter how we choose the sample points . To simplify the calculation of the integral

we often take the sample points to be right endpoints. Then and the deﬁnition of

an integral simpliﬁes as follows.

THEOREM If is integrable on , then

where and

EXAMPLE 1 Express

as an integral on the interval .

SOLUTION Comparing the given limit with the limit in Theorem 4, we see that they will

be identical if we choose . We are given that and .

Therefore, by Theorem 4, we have

M

Later, when we apply the deﬁnite integral to physical situations, it will be important to

recognize limits of sums as integrals, as we did in Example 1. When Leibniz chose the

notation for an integral, he chose the ingredients as reminders of the limiting process. In

general, when we write

we replace by , by x, and by dx.(xx

i

*

xlim

,

lim

n l '

&

n

i!1

f !x

i

*

" (x !

y

b

a

f !x" dx

lim

n l '

&

n

i!1

!x

i

3

! x

i

sin x

i

" (x !

y

#

0

!x

3

! x sin x" dx

b !

#

a ! 0f !x" ! x

3

! x sin x

)0,

#

*

lim

n l '

&

n

i!1

!x

i

3

! x

i

sin x

i

" (x

x

i

! a ! i (x(x !

b % a

n

y

b

a

f !x" dx ! lim

n

l

'

&

n

i!1

f !x

i

"

(x

)a, b*f

4

x

i

*

! x

i

x

i

*

)a, b*f

x

b

a

f !x" dx

)a, b*f

f)a, b*f

3

NOTE 5

y

b

a

f !x" dx ! lim

max (x

i

l

0

&

n

i!1

f !x

i

*

" (x

i

max (x

i

(x

1

, (x

2

, . . . , (x

n

302

|| ||

CHAPTER 5 INTEGRALS

EVALUATING INTEGRALS

When we use a limit to evaluate a deﬁnite integral, we need to know how to work with

sums. The following three equations give formulas for sums of powers of positive integers.

Equation 5 may be familiar to you from a course in algebra. Equations 6 and 7 were dis-

cussed in Section 5.1 and are proved in Appendix E.

The remaining formulas are simple rules for working with sigma notation:

EXAMPLE 2

(a) Evaluate the Riemann sum for taking the sample points to be right

endpoints and a ! 0, b ! 3, and n ! 6.

(b) Evaluate .

SOLUTION

(a) With n ! 6 the interval width is

and the right endpoints are , , , , , and

. So the Riemann sum is

! %3.9375

!

1

2

!%2.875 % 5 % 5.625 % 4 ! 0.625 ! 9"

! f !0.5" (x ! f !1.0" (x ! f !1.5" (x ! f !2.0" (x ! f !2.5" (x ! f !3.0" (x

R

6

!

&

6

i!1

f !x

i

" (x

x

6

! 3.0

x

5

! 2.5x

4

! 2.0x

3

! 1.5x

2

! 1.0x

1

! 0.5

(x !

b % a

n

!

3 % 0

6

!

1

2

y

3

0

!x

3

% 6x" dx

f !x" ! x

3

% 6x

&

n

i!1

!a

i

% b

i

" !

&

n

i!1

a

i

%

&

n

i!1

b

i

11

&

n

i!1

!a

i

! b

i

" !

&

n

i!1

a

i

!

&

n

i!1

b

i

10

&

n

i!1

ca

i

! c

&

n

i!1

a

i

9

&

n

i!1

c ! nc

8

&

n

i!1

i

3

!

$

n!n ! 1"

2

%

2

7

&

n

i!1

i

2

!

n!n ! 1"!2n ! 1"

6

&

n

i!1

i !

n!n ! 1"

2

5

N Formulas 8–11 are proved by writing out

each side in expanded form. The left side of

Equation 9 is

The right side is

These are equal by the distributive property. The

other formulas are discussed in Appendix E.

c!a

1

! a

2

! & & & ! a

n

"

ca

1

! ca

2

! & & & ! ca

n

SECTION 5.2 THE DEFINITE INTEGRAL

|| ||

303

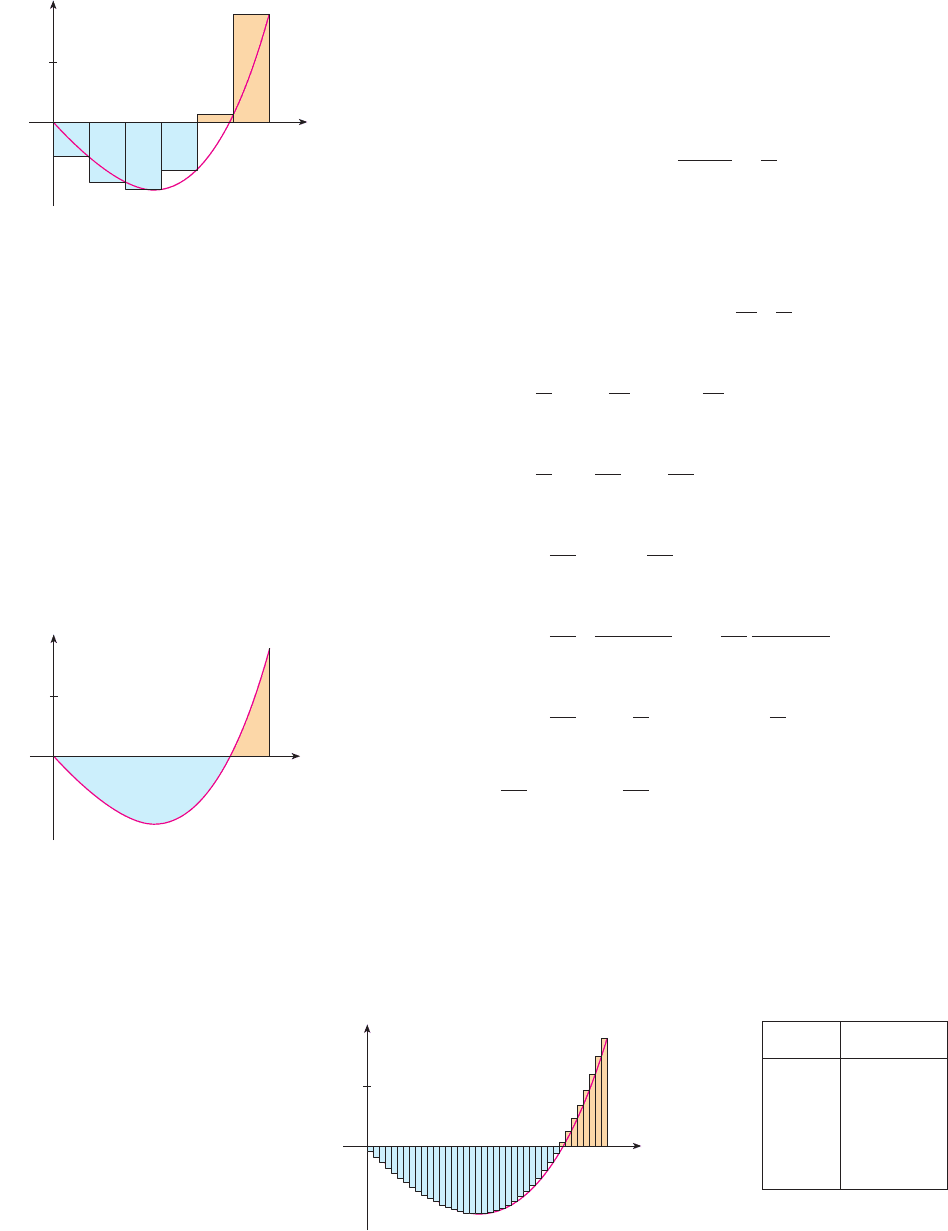
Notice that f is not a positive function and so the Riemann sum does not represent a sum

of areas of rectangles. But it does represent the sum of the areas of the gold rectangles

(above the x-axis) minus the sum of the areas of the blue rectangles (below the x-axis) in

Figure 5.

(b) With n subintervals we have

Thus , , , , and, in general, . Since we are

using right endpoints, we can use Theorem 4:

(Equation 9 with )

(Equations 11 and 9)

(Equations 5 and 7)

This integral can’t be interpreted as an area because takes on both positive and nega-

tive values. But it can be interpreted as the difference of areas , where and

are shown in Figure 6.

Figure 7 illustrates the calculation by showing the positive and negative terms in the

right Riemann sum for . The values in the table show the Riemann sums

approaching the exact value of the integral, , as .

M

0

y

3

x

5

y=˛-6x

F I G U R E 7

R¢¸Å_6.3998

n l '%6.75

n ! 40R

n

A

2

A

1

A

1

% A

2

f

!

81

4

% 27 ! %

27

4

! %6.75

! lim

n l '

$

81

4

'

1 !

1

n

(

2

% 27

'

1 !

1

n

(%

! lim

n l '

-

81

n

4

$

n!n ! 1"

2

%

2

%

54

n

2

n!n ! 1"

2

.

! lim

n l '

$

81

n

4

&

n

i!1

i

3

%

54

n

2

&

n

i!1

i

%

! lim

n l '

3

n

&

n

i!1

$

27

n

3

i

3

%

18

n

i

%

c ! 3#n ! lim

n l '

3

n

&

n

i!1

$'

3i

n

(

3

% 6

'

3i

n

(%

y

3

0

!x

3

% 6x" dx ! lim

n l '

&

n

i!1

f !x

i

" (x ! lim

n l '

&

n

i!1

f

'

3i

n

(

3

n

x

i

! 3i#nx

3

! 9#nx

2

! 6#nx

1

! 3#nx

0

! 0

(x !

b % a

n

!

3

n

0

y

3

x

5

y=˛-6x

F I G U R E 5

F I G U R E 6

j

(˛-6x)dx=A¡-A™=_6.75

0

3

A™

A¡

0

y

3

x

5

y=˛-6x

n

40 %6.3998

100 %6.6130

500 %6.7229

1000 %6.7365

5000 %6.7473

R

n

304

|| ||

CHAPTER 5 INTEGRALS

N In the sum, is a constant (unlike ), so we

can move in front of the sign.

,

3#n

in

A much simpler method for evaluating the integral in Example 2 will be given in

Section 5.3.

EXAMPLE 3

(a) Set up an expression for as a limit of sums.

(b) Use a computer algebra system to evaluate the expression.

SOLUTION

(a) Here we have and

So , , , , and

From Theorem 4, we get

(b) If we ask a computer algebra system to evaluate the sum and simplify, we obtain

Now we ask the computer algebra system to evaluate the limit:

We will learn a much easier method for the evaluation of integrals in the next section. M

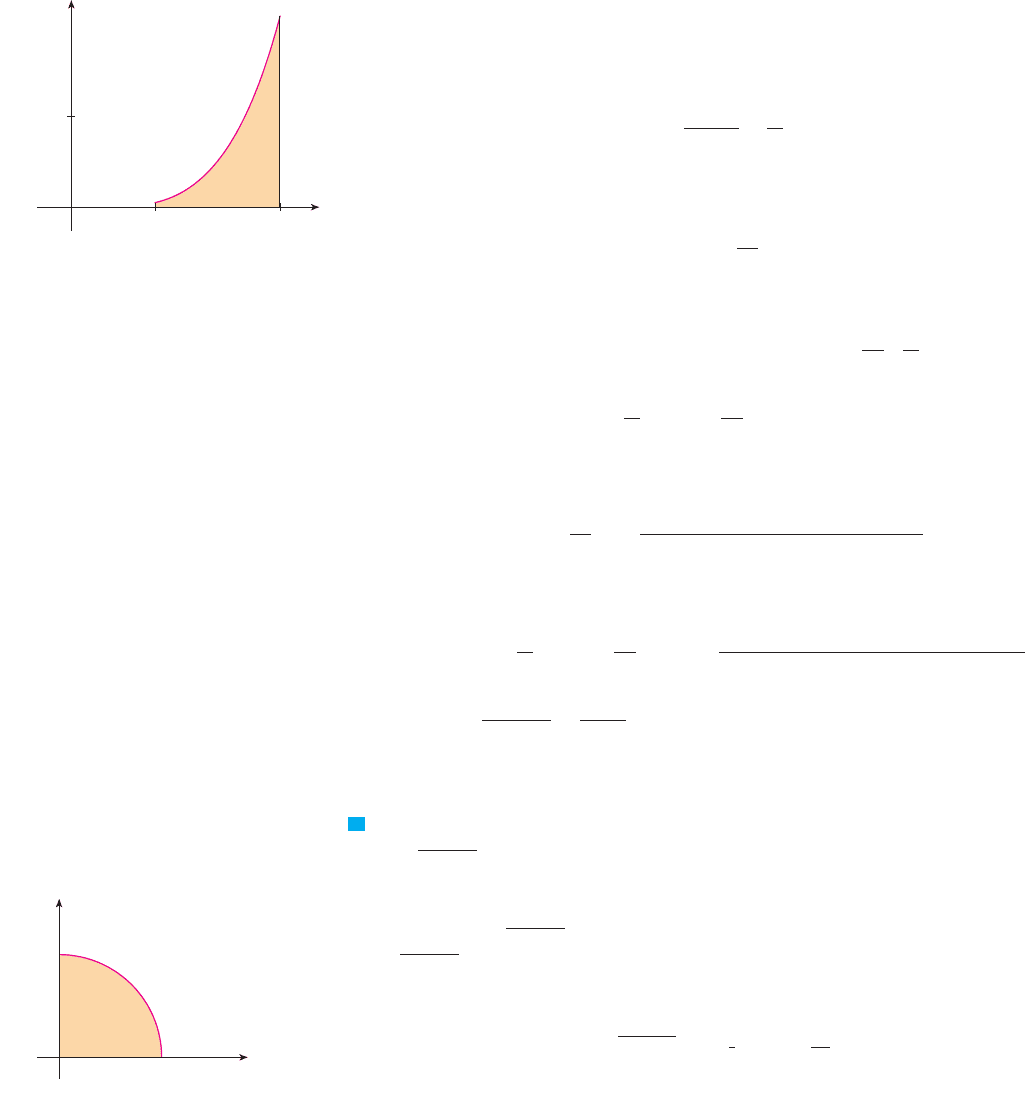
EXAMPLE 4 Evaluate the following integrals by interpreting each in terms of areas.

(a) (b)

SOLUTION

(a) Since , we can interpret this integral as the area under the curve

from 0 to 1. But, since , we get , which shows

that the graph of is the quarter-circle with radius 1 in Figure 9. Therefore

(In Section 8.3 we will be able to prove that the area of a circle of radius r is .)

#

r

2

y

1

0

s

1 % x

2

dx !

1

4

#

!1"

2

!

#

4

f

x

2

! y

2

! 1y

2

! 1 % x

2

y !

s

1 % x

2

f !x" !

s

1 % x

2

+ 0

y

3

0

!x % 1" dx

y

1

0

s

1 % x

2

dx

V

!

3!2062"

10

!

3093

5

! 618.6

y

5

2

x

4

dx ! lim

n

l

'

3

n

&

n

i!1

'

2 !

3i

n

(

4

! lim

n

l

'

3!2062n

4

! 3045n

3

! 1170n

2

% 27"

10n

4

&

n

i!1

'

2 !

3i

n

(

4

!

2062n

4

! 3045n

3

! 1170n

2

% 27

10n

3

! lim

n l '

3

n

&

n

i!1

'

2 !

3i

n

(

4

y

5

2

x

4

dx ! lim

n l '

&

n

i!1

f !x

i

" (x ! lim

n l '

&

n

i!1

f

'

2 !

3i

n

(

3

n

x

i

! 2 !

3i

n

x

3

! 2 ! 9#nx

2

! 2 ! 6#nx

1

! 2 ! 3#nx

0

! 2

(x !

b % a

n

!

3

n

f !x" ! x

4

, a ! 2, b ! 5,

x

5

2

x

4

dx

N Because is positive, the integral in

Example 3 represents the area shown in Figure 8.

f !x" ! x

4

F I G U R E 8

x

y

0

2 5

y=x$

300

y

1

0

1

x

y= 1-≈

or

≈+¥=1

œ

„„„„„

F I G U R E 9

SECTION 5.2 THE DEFINITE INTEGRAL

|| ||

305

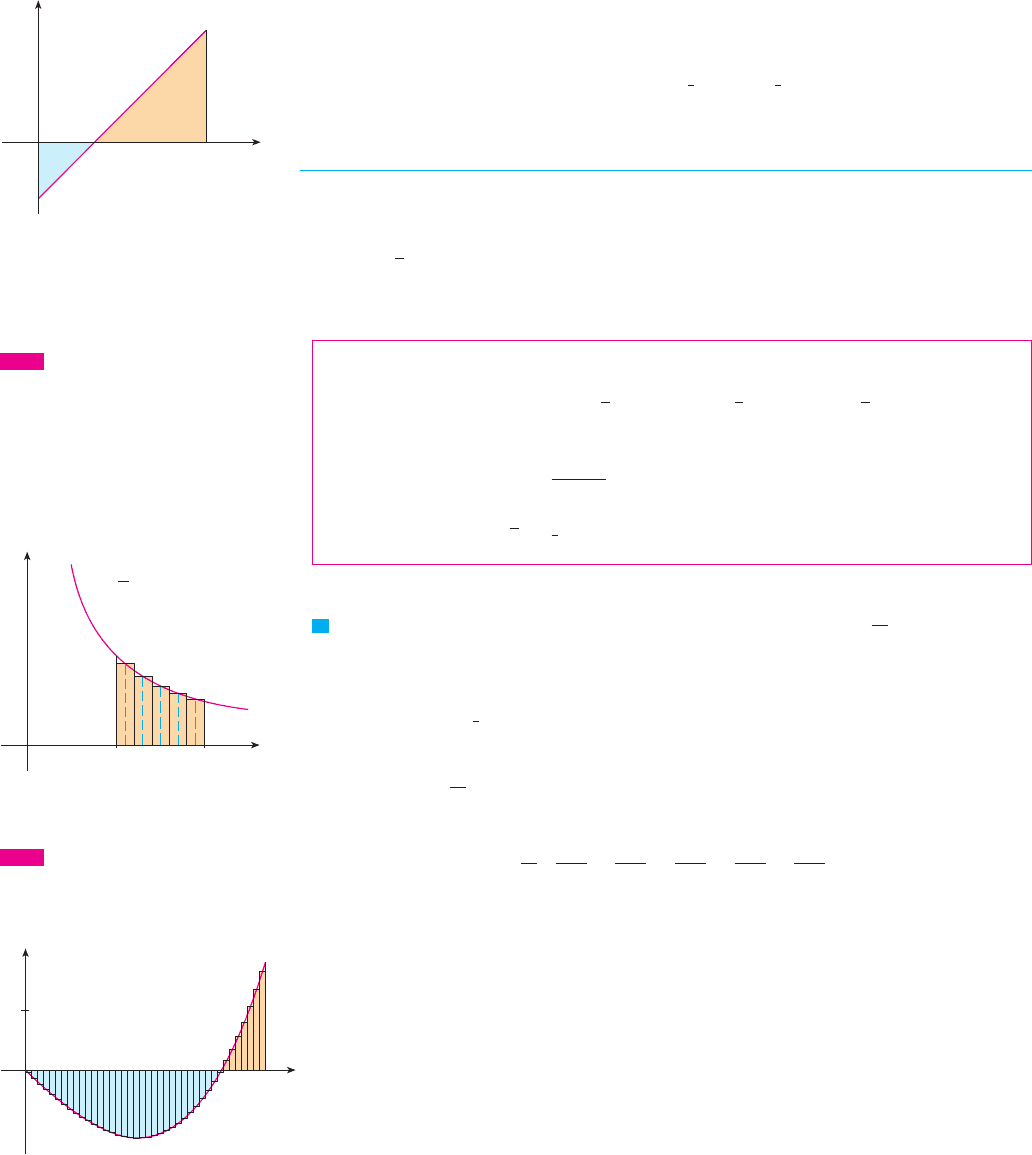
(b) The graph of is the line with slope 1 shown in Figure 10. We compute the

integral as the difference of the areas of the two triangles:

M

THE MIDPOINT RULE

We often choose the sample point to be the right endpoint of the th subinterval because

it is convenient for computing the limit. But if the purpose is to ﬁnd an approximation to

an integral, it is usually better to choose to be the midpoint of the interval, which we

denote by . Any Riemann sum is an approximation to an integral, but if we use midpoints

we get the following approximation.

MIDPOINT RULE

where

and

EXAMPLE 5 Use the Midpoint Rule with to approximate .

SOLUTION The endpoints of the ﬁve subintervals are , , , , , and ,

so the midpoints are , , , , and . The width of the subintervals is

, so the Midpoint Rule gives

Since for , the integral represents an area, and the approxi-

mation given by the Midpoint Rule is the sum of the areas of the rectangles shown in

Figure 11.

M

At the moment we don’t know how accurate the approximation in Example 5 is, but in

Section 8.7 we will learn a method for estimating the error involved in using the Midpoint

Rule. At that time we will discuss other methods for approximating deﬁnite integrals.

If we apply the Midpoint Rule to the integral in Example 2, we get the picture in Fig-

ure 12. The approximation is much closer to the true value than the

right endpoint approximation, , shown in Figure 7.R

40

/ %6.3998

%6.75M

40

/ %6.7563

1 " x " 2f !x" ! 1#x $ 0

/ 0.691908

!

1

5

'

1

1.1

!

1

1.3

!

1

1.5

!

1

1.7

!

1

1.9

(

y

2

1

x

dx / (x ) f !1.1" ! f !1.3" ! f !1.5" ! f !1.7" ! f !1.9"*

(x ! !2 % 1"#5 !

1

5

1.91.71.51.31.1

2.01.81.61.41.21

y

2

1

x

dxn ! 5

V

x

i

!

1

2

!x

i%1

! x

i

" ! midpoint of )x

i%1

, x

i

*

(x !

b % a

n

y

b

a

f !x" dx /

&

n

i!1

f !x

i

" (x ! (x ) f !x

1

" ! & & & ! f !x

n

"*

x

i

x

i

*

ix

i

*

y

3

0

!x % 1" dx ! A

1

% A

2

!

1

2

!2 & 2" %

1

2

!1 & 1" ! 1.5

y ! x % 1

F I G U R E 1 1

0

x

y

1 2

y=

1

x

Module 5.2/8.7 shows how the

Midpoint Rule estimates improve as

increases.

n

TE C

In Visual 5.2 you can compare left,

right, and midpoint approximations to the

integral in Example 2 for different values

of .n

TE C

306

|| ||

CHAPTER 5 INTEGRALS

x

y

1

0

_1

3

y=x-1

A¡

(3,2)

A™

F I G U R E 1 0

F I G U R E 1 2

M¢¸Å_6.7563

0

y

3

x

5

y=˛-6x

PROPERTIES OF THE DEFINITE INTEGRAL

When we deﬁned the deﬁnite integral , we implicitly assumed that . But the

deﬁnition as a limit of Riemann sums makes sense even if . Notice that if we reverse

a and b, then changes from to . Therefore

If , then and so

We now develop some basic properties of integrals that will help us to evaluate integrals

in a simple manner. We assume that f and t are continuous functions.

PROPERTIES OF THE INTEGRAL

1.

, where c is any constant

2.

3.

, where c is any constant

4.

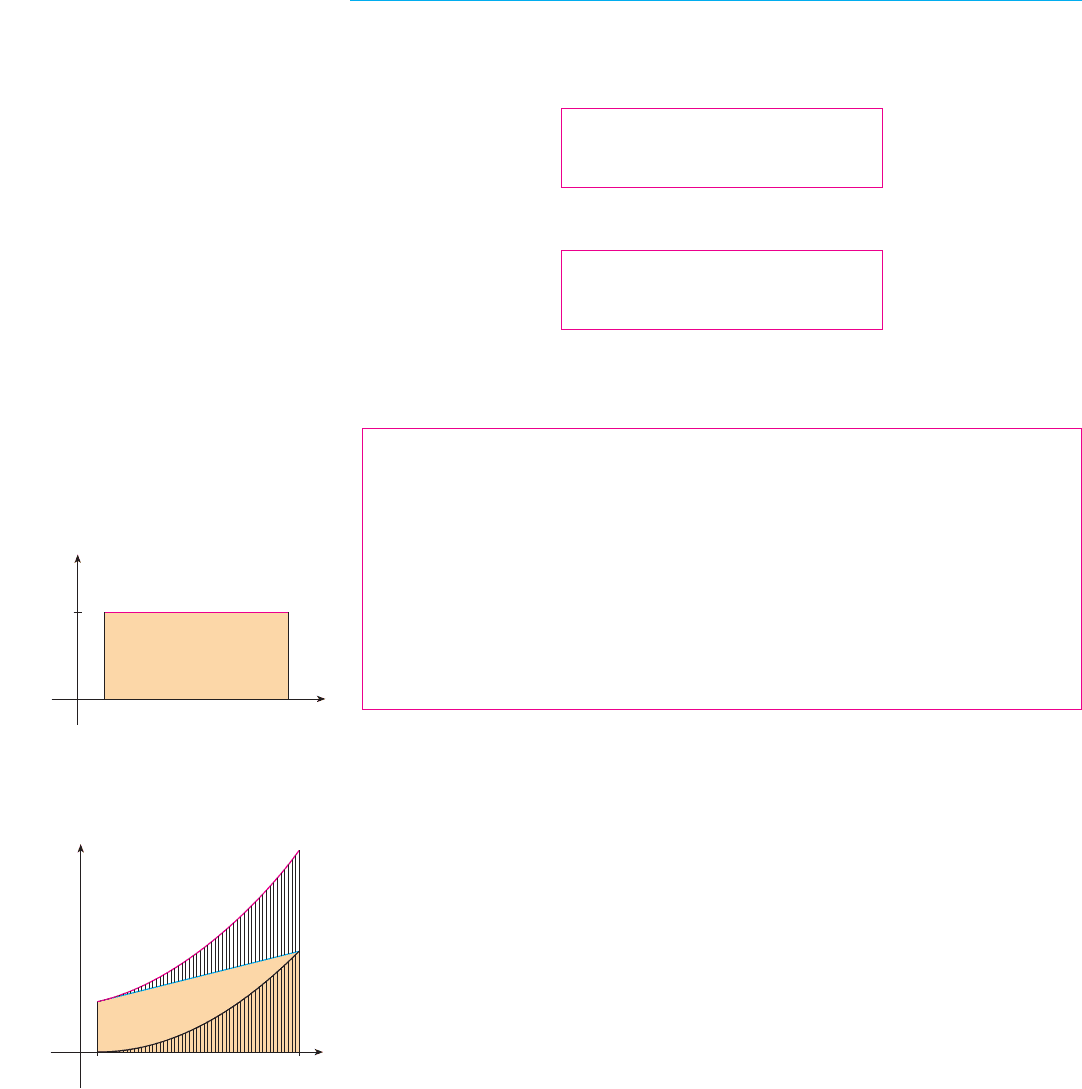
Property 1 says that the integral of a constant function is the constant times

the length of the interval. If and , this is to be expected because is

the area of the shaded rectangle in Figure 13.

Property 2 says that the integral of a sum is the sum of the integrals. For positive func-

tions it says that the area under is the area under plus the area under t. Figure 14

helps us understand why this is true: In view of how graphical addition works, the corre-

sponding vertical line segments have equal height.

In general, Property 2 follows from Theorem 4 and the fact that the limit of a sum is the

sum of the limits:

!

y

b

a

f !x" dx !

y

b

a

t!x" dx

! lim

n l '

&

n

i!1

f !x

i

" (x ! lim

n l '

&

n

i!1

t!x

i

" (x

! lim

n l '

$

&

n

i!1

f !x

i

" (x !

&

n

i!1

t!x

i

" (x

%

y

b

a

) f !x" ! t!x"* dx ! lim

n l '

&

n

i!1

) f !x

i

" ! t!x

i

"* (x

ff ! t

c!b % a"a

)

bc $ 0

f !x" ! c

y

b

a

) f !x" % t!x"* dx !

y

b

a

f !x" dx %

y

b

a

t!x" dx

y

b

a

cf !x" dx ! c

y

b

a

f !x" dx

y

b

a

) f !x" ! t!x"* dx !

y

b

a

f !x" dx !

y

b

a

t!x" dx

y

b

a

c dx ! c!b % a"

y

a

f !x" dx ! 0

(x ! 0a ! b

y

a

b

f !x" dx ! %

y

b

a

f !x" dx

!a % b"#n!b % a"#n(x

a $ b

a

)

bx

b

a

f !x" dx

F I G U R E 1 3

j

cdx=c(b-a)

a

b

0

y

x

a b

c

y=c

area=c(b-a)

SECTION 5.2 THE DEFINITE INTEGRAL

|| ||

307

y

0 x

a b

f

g

f+g

F I G U R E 1 4

j

[ƒ+©]dx=

j

ƒdx+

j

©dx

a

b

a

b

a

b

Property 3 can be proved in a similar manner and says that the integral of a constant

times a function is the constant times the integral of the function. In other words, a con-

stant (but only a constant) can be taken in front of an integral sign. Property 4 is proved by

writing and using Properties 2 and 3 with .

EXAMPLE 6 Use the properties of integrals to evaluate .

SOLUTION Using Properties 2 and 3 of integrals, we have

We know from Property 1 that

and we found in Example 2 in Section 5.1 that . So

M

The next property tells us how to combine integrals of the same function over adjacent

intervals:

5.

This is not easy to prove in general, but for the case where and

Property 5 can be seen from the geometric interpretation in Figure 15: The area under

from a to c plus the area from c to b is equal to the total area from a to b.

EXAMPLE 7 If it is known that and ,

ﬁnd .

SOLUTION By Property 5, we have

so

M

Properties 1–5 are true whether , , or . The following properties, in

which we compare sizes of functions and sizes of integrals, are true only if a ! b.

a " ba ! ba

#

b

y

10

8

f !x" dx !

y

10

0

f !x" dx $

y

8

0

f !x" dx ! 17 $ 12 ! 5

y

8

0

f !x" dx %

y

10

8

f !x" dx !

y

10

0

f !x" dx

x

10

8

f !x" dx

x

8

0

f !x" dx ! 12x

10

0

f !x" dx ! 17

V

y ! f !x"

a

#

c

#

bf !x" & 0

y

c

a

f !x" dx %

y

b

c

f !x" dx !

y

b

a

f !x" dx

! 4 % 3 '

1

3

! 5

y

1

0

!4 % 3x

2

" dx !

y

1

0

4 dx % 3

y

1

0

x

2

dx

y

1

0

x

2

dx !

1

3

y

1

0

4 dx ! 4!1 $ 0" ! 4

!

y

1

0

4 dx % 3

y

1

0

x

2

dx

y

1

0

!4 % 3x

2

" dx !

y

1

0

4 dx %

y

1

0

3x

2

dx

y

1

0

!4 % 3x

2

" dx

c ! $1f $ t ! f % !$t"

308

|| ||

CHAPTER 5 INTEGRALS

N Property 3 seems intuitively reasonable

because we know that multiplying a function

by a positive number stretches or shrinks its

graph vertically by a factor of . So it stretches

or shrinks each approximating rectangle by a

factor and therefore it has the effect of

multiplying the area by .c

c

FIG URE 15

0

y

x

a bc

y=ƒ

COMPARISON PROPERTIES OF THE INTEGRAL

6.

If for , then .

7. If for , then .

8. If for , then

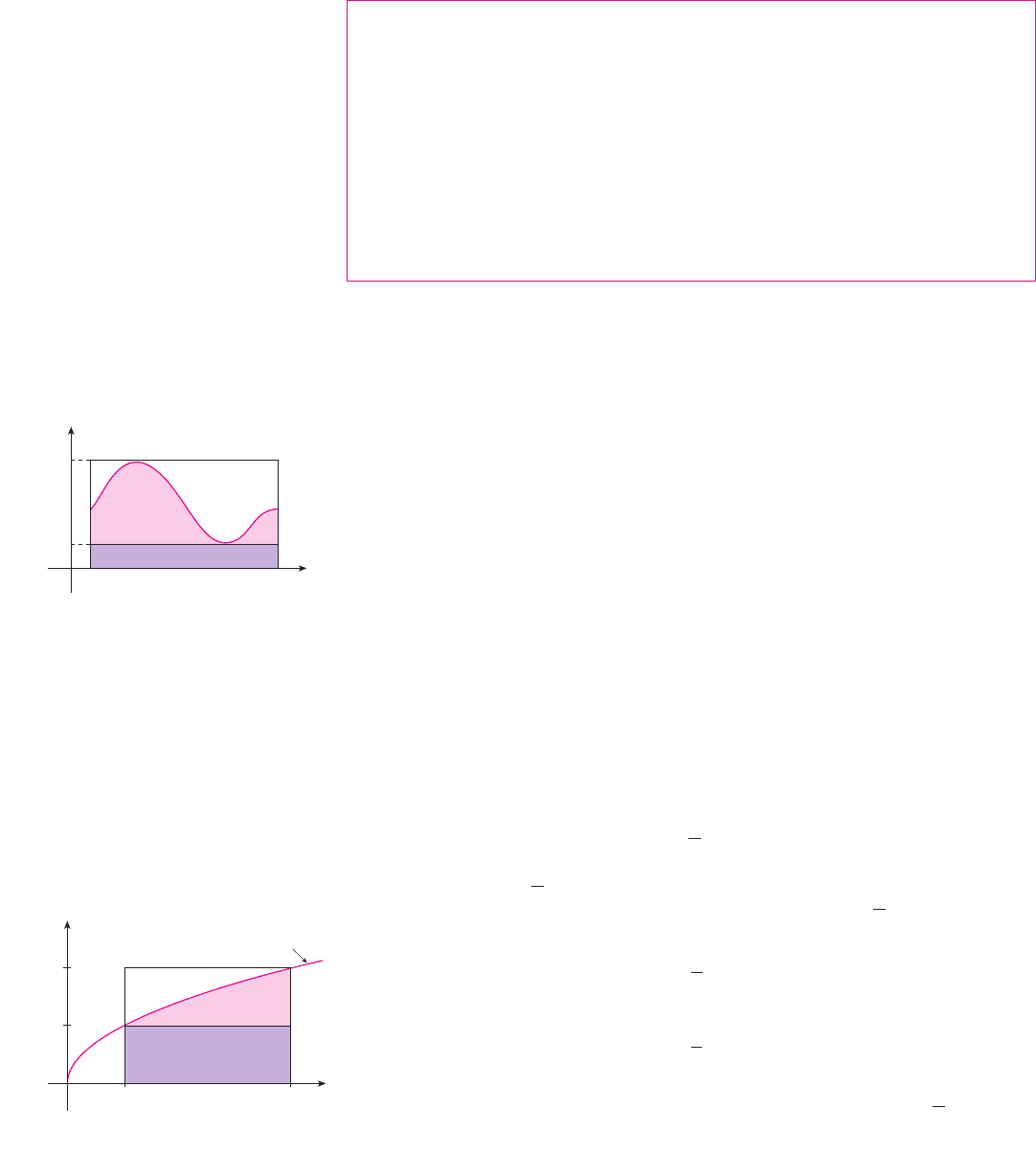
If , then represents the area under the graph of , so the geometric

interpretation of Property 6 is simply that areas are positive. But the property can be

proved from the deﬁnition of an integral (Exercise 64). Property 7 says that a bigger func-

tion has a bigger integral. It follows from Properties 6 and 4 because

Property 8 is illustrated by Figure 16 for the case where . If is continuous we

could take and to be the absolute minimum and maximum values of on the inter-

val . In this case Property 8 says that the area under the graph of is greater than the

area of the rectangle with height and less than the area of the rectangle with height .

PROOF OF PROPERTY 8 Since , Property 7 gives

Using Property 1 to evaluate the integrals on the left and right sides, we obtain

M

Property 8 is useful when all we want is a rough estimate of the size of an integral with-

out going to the bother of using the Midpoint Rule.

EXAMPLE 8 Use Property 8 to estimate

SOLUTION Since is an increasing function, its absolute minimum on is

and its absolute maximum on is . Thus

Property 8 gives

or

M

The result of Example 8 is illustrated in Figure 17. The area under from 1 to 4

is greater than the area of the lower rectangle and less than the area of the large rectangle.

y !

s

x

3 !

y

4

1

s

x

dx ! 6

1!4 $ 1" !

y

4

1

s

x

dx ! 2!4 $ 1"

M ! f !4" !

s

4

! 2#1, 4$m ! f !1" ! 1

#1, 4$f !x" !

s

x

y

4

1

s

x

dx.

m!b $ a" !

y

b

a

f !x" dx ! M!b $ a"

y

b

a

m dx !

y

b

a

f !x" dx !

y

b

a

M dx

m ! f !x" ! M

Mm

f#a, b$

fMm

ff !x" & 0

f $ t & 0.

fx

b

a

f !x" dxf !x" & 0

m!b $ a" !

y

b

a

f !x" dx ! M!b $ a"

a ! x ! bm ! f !x" ! M

y

b

a

f !x" dx &

y

b

a

t!x" dxa ! x ! bf !x" & t!x"

y

b

a

f !x" dx & 0a ! x ! bf !x" & 0

SECTION 5.2 THE DEFINITE INTEGRAL

|| ||

309

0

y

m

M

x

a b

y=ƒ

FIG URE 16

y

x

1 4

0

1

2

y=œ„x

FIG URE 17

310

|| ||

CHAPTER 5 INTEGRALS

7. A table of values of an increasing function is shown. Use

the table to ﬁnd lower and upper estimates for .

8. The table gives the values of a function obtained from an

experiment. Use them to estimate using three equal

subintervals with (a) right endpoints, (b) left endpoints, and

(c) midpoints. If the function is known to be an increasing

function, can you say whether your estimates are less than or

greater than the exact value of the integral?

9–12 Use the Midpoint Rule with the given value of to approx-

imate the integral. Round the answer to four decimal places.

10. ,

11. 12.

13. If you have a CAS that evaluates midpoint approximations

and graphs the corresponding rectangles (use middlesum

and middlebox commands in Maple), check the answer to

Exercise 11 and illustrate with a graph. Then repeat with

and .

14. With a programmable calculator or computer (see the instruc-

tions for Exercise 7 in Section 5.1), compute the left and right

Riemann sums for the function on the interval

with . Explain why these estimates show that

Deduce that the approximation using the Midpoint Rule with

in Exercise 11 is accurate to two decimal places.

15. Use a calculator or computer to make a table of values of

right Riemann sums for the integral with

, 10, 50, and 100. What value do these numbers appear

to be approaching?

16. Use a calculator or computer to make a table of values of

left and right Riemann sums and for the integral

with , 10, 50, and 100. Between what two

numbers must the value of the integral lie? Can you make a

similar statement for the integral ? Explain.

x

2

$1

s

1 % x

4

dx

n ! 5

x

2

0

s

1 % x

4

dx

R

n

L

n

n ! 5

x

(

0

sin x dxR

n

n ! 5

0.306

#

y

1

0

sin!x

2

" dx

#

0.315

n ! 100#0, 1$

f !x" ! sin!x

2

"

n ! 20n ! 10

CAS

y

5

1

x $ 1

x % 1

dx, n ! 4

y

1

0

sin!x

2

" dx, n ! 5

n ! 4

y

(

%2

0

cos

4

x dx

y

10

2

s

x

3

% 1 dx, n ! 4

9.

n

x

9

3

f !x" dx

x

25

0

f !x" dx

f

1. Evaluate the Riemann sum for , ,

with six subintervals, taking the sample points to be left end-

points. Explain, with the aid of a diagram, what the Riemann

sum represents.

2. If , , evaluate the Riemann sum

with , taking the sample points to be right endpoints.

What does the Riemann sum represent? Illustrate with a

diagram.

3. If , ﬁnd the Riemann sum with

correct to six decimal places, taking the sample points

to be midpoints. What does the Riemann sum represent?

Illustrate with a diagram.

4. (a) Find the Riemann sum for , ,

with six terms, taking the sample points to be right

endpoints. (Give your answer correct to six decimal

places.) Explain what the Riemann sum represents with

the aid of a sketch.

(b) Repeat part (a) with midpoints as sample points.

The graph of a function is given. Estimate using

four subintervals with (a) right endpoints, (b) left endpoints,

and (c) midpoints.

6. The graph of is shown. Estimate with six sub-

intervals using (a) right endpoints, (b) left endpoints, and

(c) midpoints.

x

y

0

g

1

x

3

$3

t!x" dxt

x

y

0

f

1

x

8

0

f !x" dxf

5.

0 ! x ! 3

(

%2f !x" ! sin x

n ! 5

f !x" !

s

x

$ 2, 1 ! x ! 6

n ! 6

0 ! x ! 3f !x" ! x

2

$ 2x

2 ! x ! 14f !x" ! 3 $

1

2

x

E X E R C I S E S

5.2

x 0 5 10 15 20 25

$42 $37 $25 $6 15 36f !x"

x 3 4 5 6 7 8 9

0.3 0.9 1.4 1.8$0.6$2.1$3.4f !x"

(c) (d)

34. The graph of t consists of two straight lines and a semicircle.

Use it to evaluate each integral.

(a) (b) (c)

35– 40 Evaluate the integral by interpreting it in terms of areas.

35. 36.

38.

39. 40.

41. Evaluate .

42. Given that , what is

?

43. In Example 2 in Section 5.1 we showed that .

Use this fact and the properties of integrals to evaluate

.

44. Use the properties of integrals and the result of Example 3 to

evaluate .

45. Use the results of Exercises 27 and 28 and the properties of

integrals to evaluate .

46. Use the result of Exercise 27 and the fact that

(from Exercise 25 in Section 5.1),

together with the properties of integrals, to evaluate

.

x

(

%2

0

!2 cos x $ 5x" dx

x

(

%2

0

cos x dx ! 1

x

4

1

!2x

2

$ 3x % 1" dx

x

5

2

!1 % 3x

4

" dx

x

1

0

!5 $ 6x

2

" dx

x

1

0

x

2

dx !

1

3

y

0

1

3u

s

u

2

% 4

du

y

1

0

3x

s

x

2

% 4

dx ! 5

s

5

$ 8

y

(

sin

2

x cos

4

x dx

y

10

0

&

x $ 5

&

dx

y

2

$1

&

x

&

dx

y

3

$1

!3 $ 2x" dx

y

0

$3

(

1 %

s

9 $ x

2

)

dx

37.

y

2

$2

s

4 $ x

2

dx

y

3

0

(

1

2

x $ 1" dx

x

y

0

2

4 7

4

y=©

y

7

0

t!x" dx

y

6

2

t!x" dx

y

2

0

t!x" dx

x

y

0

2

4 6 82

y=ƒ

y

9

0

f !x" dx

y

7

5

f !x" dx

17–20 Express the limit as a deﬁnite integral on the given

interval.

17.

18.

,

20. ,

21–25 Use the form of the deﬁnition of the integral given in

Theorem 4 to evaluate the integral.

21. 22.

24.

25.

26. (a) Find an approximation to the integral

using a Riemann sum with right endpoints and .

(b) Draw a diagram like Figure 3 to illustrate the approxi-

mation in part (a).

(c) Use Theorem 4 to evaluate .

(d) Interpret the integral in part (c) as a difference of areas

and illustrate with a diagram like Figure 4.

27. Prove that .

28. Prove that .

29–30 Express the integral as a limit of Riemann sums. Do not

evaluate the limit.

29. 30.

31–32 Express the integral as a limit of sums. Then evaluate,

using a computer algebra system to ﬁnd both the sum and the

limit.

31. 32.

The graph of is shown. Evaluate each integral by inter-

preting it in terms of areas.

(a) (b)

y

5

0

f !x" dx

y

2

0

f !x" dx

f

33.

y

10

2

x

6

dx

y

(

0

sin 5x dx

CAS

y

2

(

0

x

2

sin x dx

y

6

2

x

1 % x

5

dx

y

b

a

x

2

dx !

b

3

$ a

3

y

b

a

x dx !

b

2

$ a

2

x

4

0

!x

2

$ 3x" dx

n ! 8

x

4

0

!x

2

$ 3x" dx

y

2

1

x

3

dx

y

5

0

!1 % 2x

3

" dx

y

2

0

!2 $ x

2

" dx

23.

y

4

1

!x

2

% 2x $ 5 " dx

y

5

$1

!1 % 3x" dx

#0, 2$lim

n

l

)

'

n

i!1

#4 $ 3!x

i

*

"

2

% 6!x

i

*

"

5

$ *x

#1, 8]lim

n

l

)

'

n

i!1

s

2x

i

*

% !x

i

*

"

2

*x

19.

lim

n

l

)

'

n

i!1

cos x

i

x

i

*x, #

(

, 2

(

$

lim

n

l

)

'

n

i!1

1 $ x

i

2

4 % x

i

2

*x, #2, 6$

SECTION 5.2 THE DEFINITE INTEGRAL

|| ||

311

Stewart J. Calculus

Подождите немного. Документ загружается.