Stewart J. Calculus

Подождите немного. Документ загружается.

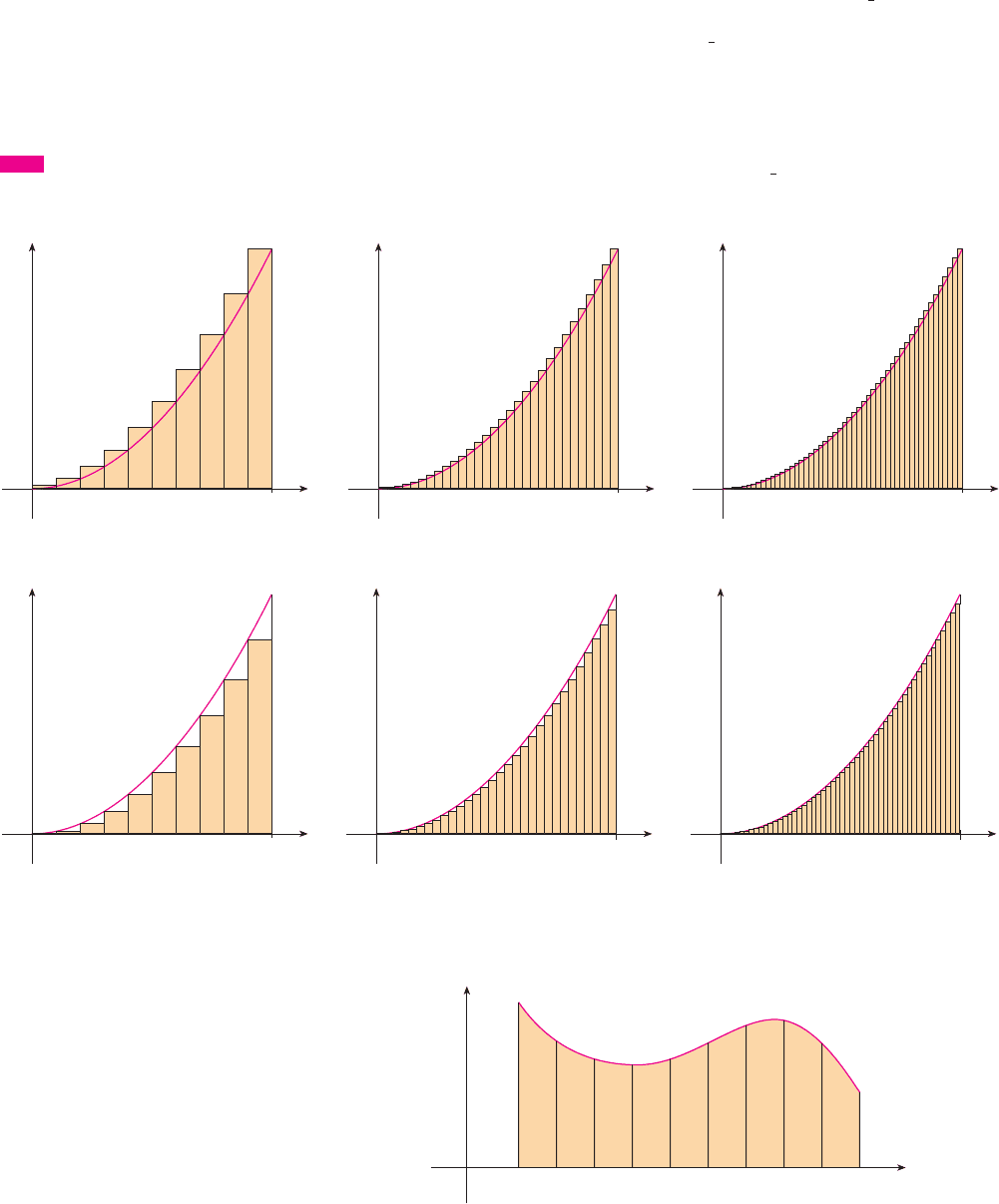
It can be shown that the lower approximating sums also approach , that is,

From Figures 8 and 9 it appears that, as n increases, both and become better and bet-

ter approximations to the area of S. Therefore, we deﬁne the area A to be the limit of the

sums of the areas of the approximating rectangles, that is,

Let’s apply the idea of Examples 1 and 2 to the more general region S of Figure 1. We

start by subdividing into strips of equal width as in Figure 10.

F I G U R E 1 0

......

y=ƒ

S¡ S™ S£

i-1

n-1

¤⁄ ‹

, S

, . . . , S

n=10 L¡¸=0.285

0 x

n=30 L£¸Å0.3169

n=50 L∞¸=0.3234

F I G U R E 9

F I G U R E 8

n=30 R£¸Å0.3502

0 x x

n=10 R¡¸=0.385

n=50 R∞¸=0.3434

A ! lim

n l $

! lim

n l $

lim

n l $

292

|| ||

CHAPTER 5 INTEGRALS

In Visual 5.1 you can create pic-

tures like those in Figures 8 and 9 for

other values of .n

TE C

The area is the number that is smaller

than all upper sums and larger than

all lower sums

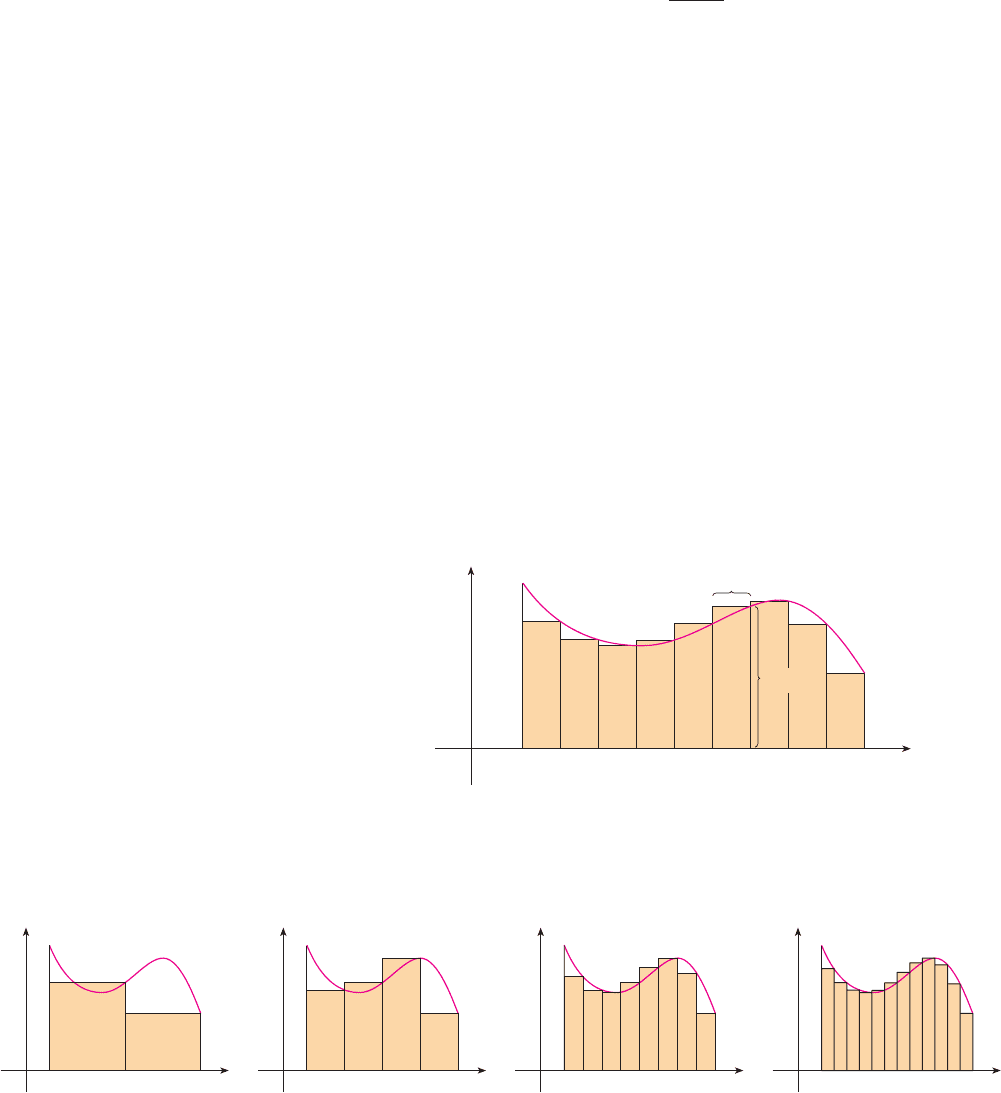
The width of the interval is , so the width of each of the n strips is

These strips divide the interval [a, b] into n subintervals

where and . The right endpoints of the subintervals are

Let’s approximate the th strip by a rectangle with width and height , which

is the value of at the right endpoint (see Figure 11). Then the area of the rectangle is

. What we think of intuitively as the area of is approximated by the sum of the

areas of these rectangles, which is

Figure 12 shows this approximation for and . Notice that this approxi-

mation appears to become better and better as the number of strips increases, that is, as

. Therefore we deﬁne the area of the region in the following way.

F I G U R E 1 2

xa ⁄

(a) n=2

xa ⁄ ¤ ‹

(b) n=4

xa b

(d) n=12

SAn l $

12n ! 2, 4, 8,

F I G U R E 1 1

Îx

f(x

)

i-1

a b

¤⁄ ‹

! f !x

" &x # f !x

" &x # % % % # f !x

" &x

Sf !x

" &x

ithf

f !x

"&xS

! a # 3 &x,

! a # 2 &x,

! a # &x,

! bx

! a

, x

*, )x

, x

*, )x

, x

*, . . . , )x

n'1

, x

&x !

b ' a

b ' a)a, b*

SECTION 5.1 AREAS AND DISTANCES

|| ||

293

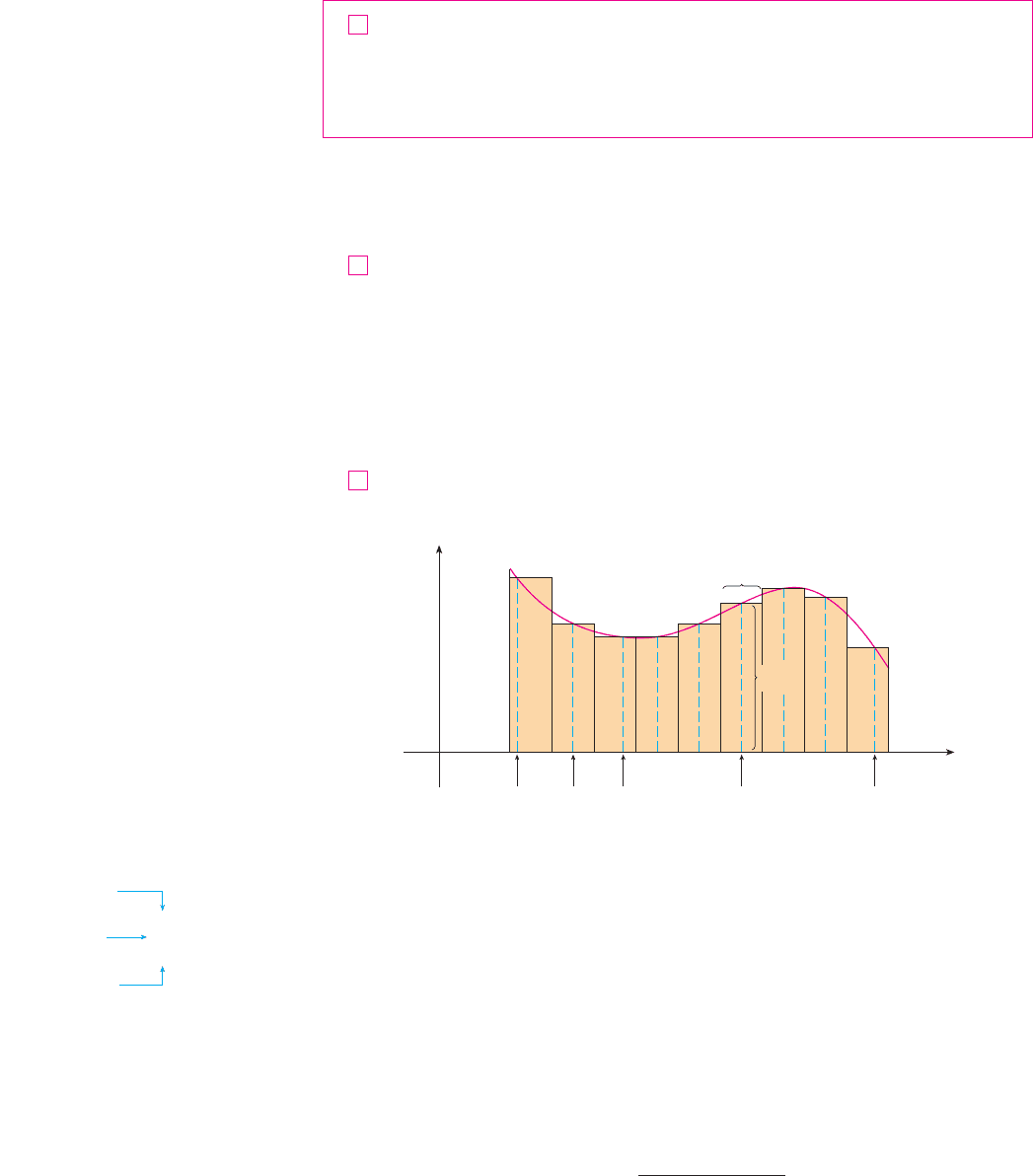
DEFINITION The area A of the region S that lies under the graph of the contin-

uous function is the limit of the sum of the areas of approximating rectangles:

It can be proved that the limit in Deﬁnition 2 always exists, since we are assuming that

is continuous. It can also be shown that we get the same value if we use left endpoints:

In fact, instead of using left endpoints or right endpoints, we could take the height of the

ith rectangle to be the value of f at any number in the ith subinterval . We call

the numbers , , . . . , the sample points. Figure 13 shows approximating rectangles

when the sample points are not chosen to be endpoints. So a more general expression for the

area of S is

We often use sigma notation to write sums with many terms more compactly. For

instance,

So the expressions for area in Equations 2, 3, and 4 can be written as follows:

We can also rewrite Formula 1 in the following way:

i!1

n!n # 1"!2n # 1"

A ! lim

i!1

f !x

" &x A ! lim

i!1

f !x

i'1

" &x A ! lim

i!1

f !x

" &x

i!1

f !x

" &x ! f !x

" &x # f !x

" &x # % % % # f !x

" &x

F I G U R E 1 3

i-1

a b

¤⁄ ‹ x

n-1

x¡

x™

x£

Îx

f(x

A ! lim

n l $

) f !x

" &x # f !x

" &x # % % % # f !x

" &x*

i'1

, x

A ! lim

n l $

! lim

n l $

) f !x

" &x # f !x

" &x # % % % # f !x

n'1

" &x*

A ! lim

n l $

! lim

n l $

) f !x

" &x # f !x

" &x # % % % # f !x

" &x*

294

|| ||

CHAPTER 5 INTEGRALS

N If you need practice with sigma notation, look

at the examples and try some of the exercises in

Appendix E.

This tells us to

end with i=n.

This tells us

to add.

This tells us to

start with i=m.

f(x

)Î

i=m

EXAMPLE 3 Let A be the area of the region that lies under the graph of

between and , where .

(a) Using right endpoints, ﬁnd an expression for A as a limit. Do not evaluate the limit.

(b) Estimate the area for the case by taking the sample points to be midpoints

and using four subintervals.

SOLUTION

(a) Since , the width of a subinterval is

So , and . The sum of the areas of

the approximating rectangles is

According to Deﬁnition 2, the area is

Using sigma notation we could write

It is very difﬁcult to evaluate this limit directly by hand, but with the aid of a computer

algebra system it isn’t hard (see Exercise 25). In Section 5.3 we will be able to ﬁnd A

more easily using a different method.

(b) With and we have , so the subintervals are

, , , and . The midpoints of these subintervals

are

and the sum of the areas of the four approximating rectangles (see Figure 14) is

(

cos

(

# cos

(

# cos

(

# cos

(

& 1.006

cos

(

cos

(

cos

(

cos

(

! f !

(

%16" &x # f !3

(

%16" &x # f !5

(

%16" &x # f !7

(

%16" &x

i!1

f !x

" &x

(

%8,

(

%2*)

(

%4, 3

(

%8*)

(

%8,

(

%4*)0,

(

%8*

&x ! !

(

%2"%4 !

(

%8b !

(

%2n ! 4

A ! lim

n l $

i!1

cos

A ! lim

n l $

! lim

n l $

cos

# cos

# % % % # cos

cos

# % % % #

cos

! !cos x

" &x # !cos x

" &x # % % % # !cos x

" &x

! f !x

" &x # f !x

" &x # % % % # f !x

" &x

! nb%nx

! b%n, x

! 2b%n, x

! 3b%n, x

! ib%n

&x !

b ' 0

a ! 0

b !

(

0 ) b )

(

%2x ! bx ! 0

f !x" ! cos x

SECTION 5.1 AREAS AND DISTANCES

|| ||

295

F I G U R E 1 4

3π

y=cosx

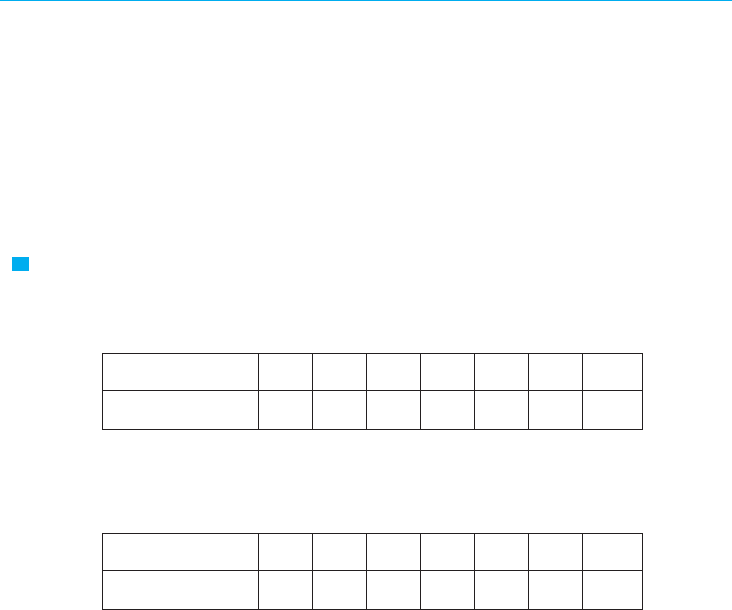
So an estimate for the area is

THE DISTANCE PROBLEM

Now let’s consider the distance problem: Find the distance traveled by an object during a

certain time period if the velocity of the object is known at all times. (In a sense this is the

inverse problem of the velocity problem that we discussed in Section 2.1.) If the velocity

remains constant, then the distance problem is easy to solve by means of the formula

But if the velocity varies, it’s not so easy to ﬁnd the distance traveled. We investigate the

problem in the following example.

EXAMPLE 4 Suppose the odometer on our car is broken and we want to estimate the

distance driven over a 30-second time interval. We take speedometer readings every ﬁve

seconds and record them in the following table:

In order to have the time and the velocity in consistent units, let’s convert the velocity

readings to feet per second (1 mi%h ! 5280%3600 ft%s):

During the ﬁrst ﬁve seconds the velocity doesn’t change very much, so we can estimate

the distance traveled during that time by assuming that the velocity is constant. If we

take the velocity during that time interval to be the initial velocity (25 ft%s), then we

obtain the approximate distance traveled during the ﬁrst ﬁve seconds:

Similarly, during the second time interval the velocity is approximately constant and we

take it to be the velocity when t ! 5 s. So our estimate for the distance traveled from

to is

If we add similar estimates for the other time intervals, we obtain an estimate for the

total distance traveled:

!25 * 5" # !31 * 5" # !35 * 5" # !43 * 5" # !47 * 5" # !46 * 5" ! 1135 ft

31 ft%s * 5 s ! 155 ft

t ! 10 st ! 5 s

25 ft%s * 5 s ! 125 ft

distance ! velocity * time

A & 1.006

296

|| ||

CHAPTER 5 INTEGRALS

Time (s) 0 5 10 15 20 25 30

Velocity (mi%h) 17 21 24 29 32 31 28

Time (s) 0 5 10 15 20 25 30

Velocity (ft%s) 25 31 35 43 47 46 41

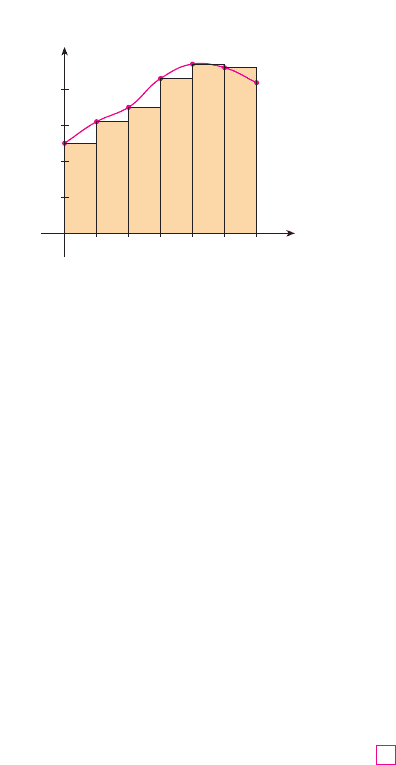
We could just as well have used the velocity at the end of each time period instead

of the velocity at the beginning as our assumed constant velocity. Then our estimate

becomes

If we had wanted a more accurate estimate, we could have taken velocity readings

every two seconds, or even every second.

Perhaps the calculations in Example 4 remind you of the sums we used earlier to esti-

mate areas. The similarity is explained when we sketch a graph of the velocity function of

the car in Figure 15 and draw rectangles whose heights are the initial velocities for each

time interval. The area of the ﬁrst rectangle is , which is also our estimate

for the distance traveled in the ﬁrst ﬁve seconds. In fact, the area of each rectangle can be

interpreted as a distance because the height represents velocity and the width represents

time. The sum of the areas of the rectangles in Figure 15 is , which is our ini-

tial estimate for the total distance traveled.

In general, suppose an object moves with velocity , where and

(so the object always moves in the positive direction). We take velocity readings

at times so that the velocity is approximately constant on each

subinterval. If these times are equally spaced, then the time between consecutive readings

is . During the ﬁrst time interval the velocity is approximately and so

the distance traveled is approximately . Similarly, the distance traveled during the

second time interval is about and the total distance traveled during the time inter-

val is approximately

If we use the velocity at right endpoints instead of left endpoints, our estimate for the total

distance becomes

The more frequently we measure the velocity, the more accurate our estimates become, so

it seems plausible that the exact distance d traveled is the limit of such expressions:

We will see in Section 5.4 that this is indeed true.

Because Equation 5 has the same form as our expressions for area in Equations 2 and

3, it follows that the distance traveled is equal to the area under the graph of the velocity

function. In Chapters 6 and 9 we will see that other quantities of interest in the natural and

social sciences—such as the work done by a variable force or the cardiac output of the

heart—can also be interpreted as the area under a curve. So when we compute areas in this

chapter, bear in mind that they can be interpreted in a variety of practical ways.

d ! lim

n l $

i!1

f !t

i'1

" &t ! lim

n l $

i!1

f !t

" &t

f !t

" &t # f !t

" &t # % % % # f !t

" &t !

i!1

f !t

" &t

f !t

" &t # f !t

" &t # % % % # f !t

n'1

" &t !

i!1

f !t

i'1

" &t

)a, b*

f !t

" &t

f !t

" &t

f !t

"&t ! !b ' a"%n

!! a", t

, t

, . . . , t

!! b"

f !t" ! 0

a ) t ) bv ! f !t"

! 1135

25 * 5 ! 125

!31 * 5" # !35 * 5" # !43 * 5" # !47 * 5" # !46 * 5" # !41 * 5" ! 1215 ft

SECTION 5.1 AREAS AND DISTANCES

|| ||

297

F I G U R E 1 5

10 20

√

points. Then improve your estimate by using six rectangles.

Sketch the curve and the approximating rectangles.

(b) Repeat part (a) using left endpoints.

(d) From your sketches in parts (a)–(c), which appears to

be the best estimate?

;

6. (a) Graph the function .

(b) Estimate the area under the graph of using four approxi-

mating rectangles and taking the sample points to be

(i) right endpoints (ii) midpoints

In each case sketch the curve and the rectangles.

rectangles.

7– 8 With a programmable calculator (or a computer), it is possible

to evaluate the expressions for the sums of areas of approximating

rectangles, even for large values of , using looping. (On a TI use

the Is command or a For-EndFor loop, on a Casio use Isz, on an

HP or in BASIC use a FOR-NEXT loop.) Compute the sum of the

areas of approximating rectangles using equal subintervals and

right endpoints for , 30, 50, and 100. Then guess the value

of the exact area.

7. The region under from to

8. The region under from to

9. Some computer algebra systems have commands that will

draw approximating rectangles and evaluate the sums of their

areas, at least if is a left or right endpoint. (For instance,

in Maple use leftbox, rightbox, leftsum, and

rightsum.)

(a) If , ﬁnd the left and right

sums for and .

(b) Illustrate by graphing the rectangles in part (a).

and 0.791.

10. (a) If , use the commands

discussed in Exercise 9 to ﬁnd the left and right sums for

30, and .

(b) Illustrate by graphing the rectangles in part (a).

and 1.624.

The speed of a runner increased steadily during the ﬁrst three

seconds of a race. Her speed at half-second intervals is given in

the table. Find lower and upper estimates for the distance that

she traveled during these three seconds.

11.

50n ! 10,

f !x" ! x#!x ! 2", 1 " x " 4

CAS

50n ! 10, 30,

f !x" ! 1#! x

! 1", 0 " x " 1

CAS

#20y ! cos x

10y ! x

n ! 10

f !x" ! 1#!1 ! x

", %2 " x " 2

1. (a) By reading values from the given graph of , use ﬁve rect-

angles to ﬁnd a lower estimate and an upper estimate for

the area under the given graph of from to .

In each case sketch the rectangles that you use.

(b) Find new estimates using ten rectangles in each case.

(a) Use six rectangles to ﬁnd estimates of each type for the

area under the given graph of from to .

(i) (sample points are left endpoints)

(ii) (sample points are right endpoints)

(iii) (sample points are midpoints)

(b) Is an underestimate or overestimate of the true area?

(d) Which of the numbers , , or gives the best

estimate? Explain.

3. (a) Estimate the area under the graph of from

to using four approximating rectangles

and right endpoints. Sketch the graph and the rectangles.

Is your estimate an underestimate or an overestimate?

(b) Repeat part (a) using left endpoints.

4. (a) Estimate the area under the graph of from

to using four approximating rectangles and

right endpoints. Sketch the graph and the rectangles. Is

your estimate an underestimate or an overestimate?

(b) Repeat part (a) using left endpoints.

(a) Estimate the area under the graph of from

to using three rectangles and right end-x ! 2x ! %1

f !x" ! 1 ! x

x ! 4x ! 0

f !x" !

x !

#2x ! 0

f !x" ! cos x

y=ƒ

8 12

x ! 12x ! 0f

y=ƒ

x ! 10x ! 0f

E X E R C I S E S

5.1

t (s) 0 0.5 1.0 1.5 2.0 2.5 3.0

(ft#s) 0 6.2 10.8 14.9 18.1 19.4 20.2

298

|| ||

CHAPTER 5 INTEGRALS

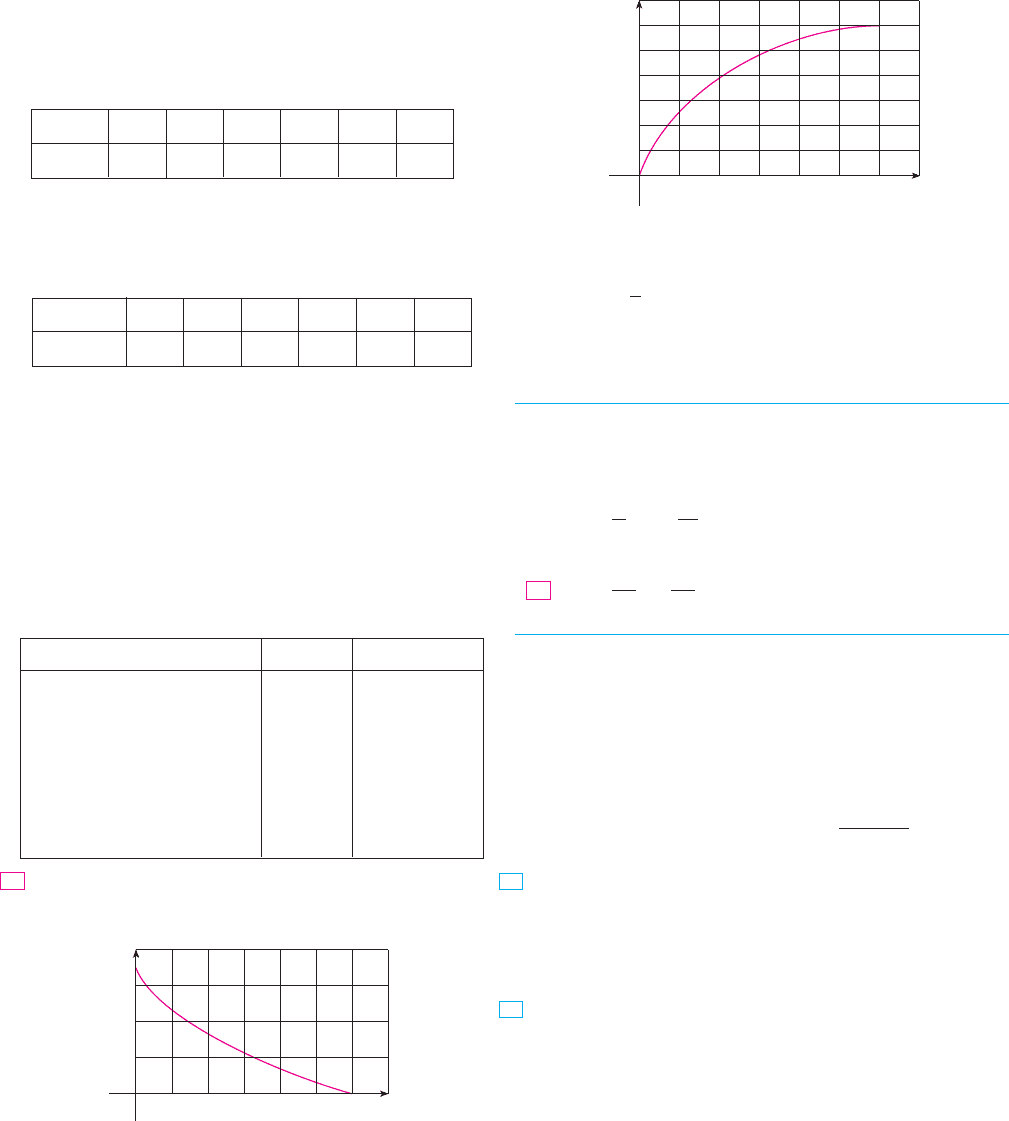
16.

The velocity graph of a car accelerating from rest to a speed

of over a period of 30 seconds is shown. Estimate

the distance traveled during this period.

17–19

Use Deﬁnition 2 to ﬁnd an expression for the area under

the graph of as a limit. Do not evaluate the limit.

17.

18.

19.

20 – 21

Determine a region whose area is equal to the given limit.

Do not evaluate the limit.

20.

22.

(a) Use Deﬁnition 2 to ﬁnd an expression for the area under

the curve from 0 to 1 as a limit.

(b) The following formula for the sum of the cubes of the

ﬁrst integers is proved in Appendix E. Use it to evaluate

the limit in part (a).

23.

(a) Express the area under the curve from 0 to 2 as

a limit.

(b) Use a computer algebra system to ﬁnd the sum in your

expression from part (a).

24.

(a) Express the area under the curve from

2 to 7 as a limit.

(b) Use a computer algebra system to evaluate the sum in

part (a).

evaluating the limit of the expression in part (b).

y ! x

! 5x

! x

CAS

y ! x

CAS

! 2

! 3

! & & & ! n

n!n ! 1"

y ! x

lim

n l '

i!1

tan

21.

lim

n l '

i!1

5 !

(

0 " x "

#2f !x" ! x cos x

2 " x " 5f !x" ! 1 ! x

1 " x " 16f !x" !

√

(km

(seconds)

20 30

120 km#h

12.

Speedometer readings for a motorcycle at 12-second intervals

are given in the table.

(a) Estimate the distance traveled by the motorcycle during

this time period using the velocities at the beginning of

the time intervals.

(b) Give another estimate using the velocities at the end of

the time periods.

estimates? Explain.

13.

Oil leaked from a tank at a rate of liters per hour. The

rate decreased as time passed and values of the rate at two-

hour time intervals are shown in the table. Find lower and

upper estimates for the total amount of oil that leaked out.

14.

When we estimate distances from velocity data, it is some-

times necessary to use times that are not

equally spaced. We can still estimate distances using the time

periods . For example, on May 7, 1992, the

space shuttle Endeavour was launched on mission STS-49,

the purpose of which was to install a new perigee kick motor

in an Intelsat communications satellite. The table, provided

by NASA, gives the velocity data for the shuttle between

liftoff and the jettisoning of the solid rocket boosters. Use

these data to estimate the height above the earth’s surface of

the Endeavour, 62 seconds after liftoff.

The velocity graph of a braking car is shown. Use it to esti-

mate the distance traveled by the car while the brakes are

applied.

√

(seconds)

4 6

(ft

15.

! t

% t

i%1

, t

, . . .

r!t"

t (s) 0 12 24 36 48 60

(ft#s) 30 28 25 22 24 27

0 2 4 6 8 10

(L#h) 8.7 7.6 6.8 6.2 5.7 5.3r!t"

t !h"

Event Time (s) Velocity (ft#s)

Launch 0 0

Begin roll maneuver 10 185

End roll maneuver 15 319

Throttle to 89% 20 447

Throttle to 67% 32 742

Throttle to 104% 59 1325

Maximum dynamic pressure 62 1445

Solid rocket booster separation 125 4151

SECTION 5.1 AREAS AND DISTANCES

|| ||

299

Openmirrors.com

THE DEFINITE INTEGRAL

We saw in Section 5.1 that a limit of the form

arises when we compute an area. We also saw that it arises when we try to ﬁnd the dis-

tance traveled by an object. It turns out that this same type of limit occurs in a wide vari-

ety of situations even when is not necessarily a positive function. In Chapters 6 and 9 we

will see that limits of the form (1) also arise in ﬁnding lengths of curves, volumes of solids,

centers of mass, force due to water pressure, and work, as well as other quantities. We

therefore give this type of limit a special name and notation.

DEFINITION OF A DEFINITE INTEGRAL

If is a function deﬁned for ,

we divide the interval into n subintervals of equal width .

We let (! b) be the endpoints of these subintervals and we

let be any sample points in these subintervals, so lies in the ith

subinterval . Then the deﬁnite integral of f from a to b is

provided that this limit exists. If it does exist, we say that is integrable on .

The precise meaning of the limit that deﬁnes the integral is as follows:

For every number there is an integer such that

for every integer and for every choice of

The symbol was introduced by Leibniz and is called an integral sign. It is

an elongated and was chosen because an integral is a limit of sums. In the notation

is called the integrand and and are called the limits of integration;

is the lower limit and is the upper limit. For now, the symbol has no meaning

by itself; is all one symbol. The simply indicates that the independent vari-

able is . The procedure of calculating an integral is called integration.x

dxx

f !x" dx

dxba

baf !x"

f !x" dx,

NOTE 1

i%1

, x

n $ N

f !x" dx %

i!1

f !x

" (x

)

N* $ 0

)a, b*f

f !x" dx ! lim

i!1

f !x

" (x

i%1

, x

, . . . , x

!! a", x

, x

, . . . , x

(x ! !b % a"#n)a, b*

a " x " bf

lim

n l '

i!1

f !x

" (x ! lim

n l '

) f !x

(x ! f !x

(x ! & & & ! f !x

(x*

5.2

into congruent triangles with central angle , show

that

(b) Show that . [Hint: Use Equation 3.4.2.]lim

sin

(

#nn

25.

Find the exact area under the cosine curve from

to , where . (Use a computer alge-

bra system both to evaluate the sum and compute the limit.)

In particular, what is the area if ?

26.

(a) Let be the area of a polygon with equal sides

inscribed in a circle with radius . By dividing the polygonr

b !

0 " b "

#2x ! bx ! 0

y ! cos x

CAS

300

|| ||

CHAPTER 5 INTEGRALS

Openmirrors.com

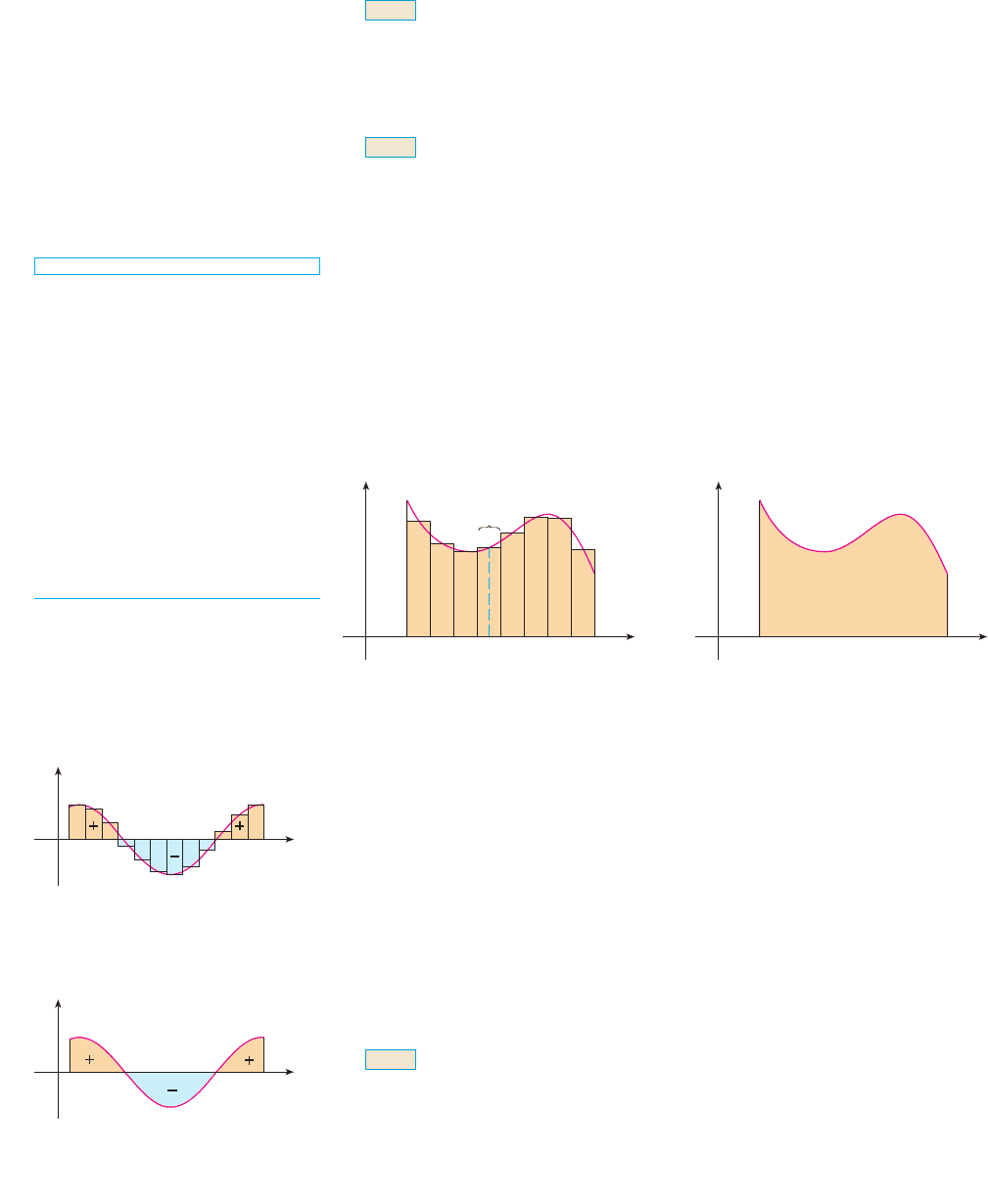
The deﬁnite integral is a number; it does not depend on . In fact, we

could use any letter in place of without changing the value of the integral:

The sum

that occurs in Deﬁnition 2 is called a Riemann sum after the German mathematician

Bernhard Riemann (1826–1866). So Deﬁnition 2 says that the deﬁnite integral of an inte-

grable function can be approximated to within any desired degree of accuracy by a Riemann

sum.

We know that if happens to be positive, then the Riemann sum can be interpreted as

a sum of areas of approximating rectangles (see Figure 1). By comparing Deﬁnition 2 with

the deﬁnition of area in Section 5.1, we see that the deﬁnite integral can be inter-

preted as the area under the curve from a to b. (See Figure 2.)

If takes on both positive and negative values, as in Figure 3, then the Riemann sum is

the sum of the areas of the rectangles that lie above the -axis and the negatives of the areas

of the rectangles that lie below the -axis (the areas of the gold rectangles minus the areas

of the blue rectangles). When we take the limit of such Riemann sums, we get the situa-

tion illustrated in Figure 4. A deﬁnite integral can be interpreted as a net area, that is, a

difference of areas:

where is the area of the region above the -axis and below the graph of , and is the

area of the region below the -axis and above the graph of .

Although we have deﬁned by dividing into subintervals of

equal width, there are situations in which it is advantageous to work with subintervals

of unequal width. For instance, in Exercise 14 in Section 5.1 NASA provided velocity data

at times that were not equally spaced, but we were still able to estimate the distance trav-

eled. And there are methods for numerical integration that take advantage of unequal

subintervals.

)a, b*

f !x" dx

NOTE 4

fxA

f !x" dx ! A

% A

Îx

F I G U R E 1

If ƒ˘0, the Riemann sum µf(x

)Îx

is the sum of areas of rectangles.

y=ƒ

F I G U R E 2

If ƒ˘0, the integral

ƒdx is the

area under the curve y=ƒ from a to b.

y ! f !x"

f !x" dx

i!1

f !x

" (x

NOTE 3

f !x" dx !

f !t" dt !

f !r" dr

f !x" dx

NOTE 2

Bernhard Riemann received his Ph.D. under the

direction of the legendary Gauss at the University

of Göttingen and remained there to teach. Gauss,

who was not in the habit of praising other mathe-

maticians, spoke of Riemann’s “creative, active,

truly mathematical mind and gloriously fertile

originality.” The deﬁnition (2) of an integral that

we use is due to Riemann. He also made major

contributions to the theory of functions of a

complex variable, mathematical physics, num-

ber theory, and the foundations of geometry.

Riemann’s broad concept of space and geometry

turned out to be the right setting, 50 years later,

for Einstein’s general relativity theory. Riemann’s

health was poor throughout his life, and he died

of tuberculosis at the age of 39.

RI E MA N N

F I G U R E 3

f(x

)Îx is an approximation to

the net area

y=ƒ

F I G U R E 4

ƒdx is the net area

SECTION 5.2 THE DEFINITE INTEGRAL

|| ||

301