Stewart J. Calculus

322

|| ||

CHAPTER 5 INTEGRALS

53. The Fresnel function was deﬁned in Example 3 and

graphed in Figures 7 and 8.

(a) At what values of does this function have local maxi-

mum values?

(b) On what intervals is the function concave upward?

(c) Use a graph to solve the following equation correct to two

decimal places:

The sine integral function

is important in electrical engineering. [The integrand

is not deﬁned when , but we know that

its limit is 1 when . So we deﬁne and this

makes a continuous function everywhere.]

(a) Draw the graph of .

(b) At what values of does this function have local maxi-

mum values?

(c) Find the coordinates of the ﬁrst inﬂection point to the

right of the origin.

(d) Does this function have horizontal asymptotes?

(e) Solve the following equation correct to one decimal place:

55–56 Let , where is the function whose graph

is shown.

(a) At what values of do the local maximum and minimum

values of occur?

(b) Where does attain its absolute maximum value?

(c) On what intervals is concave downward?

(d) Sketch the graph of .

56.

y

1

t

0

73 5 9

f

_0.2

0.2

0.4

y

2

t

0

_1

_2

1

2

4 6 8

3

f

55.

t

x

ft!x" !

x

0

f !t" dt

y

x

0

sin t

t

dt ! 1

x

Si

f

f !0" ! 1t l 0

t ! 0f !t" ! !sin t"%t

Si!x" !

y

x

0

sin t

t

dt

54.

CAS

y

x

0

sin!

'

t

2

%2" dt ! 0.2

CAS

x

S

35. where

36. where

;

37– 40 What is wrong with the equation?

37.

38.

39.

40.

;

41– 44 Use a graph to give a rough estimate of the area of the

region that lies beneath the given curve. Then ﬁnd the exact area.

41. , 42. ,

43. , 44. ,

45– 46 Evaluate the integral and interpret it as a difference of

areas. Illustrate with a sketch.

46.

47–50 Find the derivative of the function.

48.

49.

50.

51. If , where ,

ﬁnd .

52. Find the interval on which the curve

is concave upward.

y !

y

x

0

1

1 $ t $ t

2

dt

F)!2"

f !t" !

y

t

2

1

s

1 $ u

4

u

duF!x" !

y

x

1

f !t" dt

y !

y

5x

cos x

cos!u

2

" du

y !

y

x

3

s

x

s

t

sin t dt

t!x" !

y

x

2

tan x

1

s

2 $ t

4

dt

(

Hint:

y

3x

2x

f !u" du !

y

0

2x

f !u" du $

y

3x

0

f !u" du

&

t!x" !

y

3x

2x

u

2

! 1

u

2

$ 1

du

47.

y

5

'

%2

'

%4

sin x dx

y

2

!1

x

3

dx

45.

0 # x #

'

%3y ! sec

2

x0 # x #

'

y ! sin x

1 # x # 6y ! x

!4

0 # x # 27y !

s

3

x

y

'

0

sec

2

x dx ! tan x

]

0

'

!

0

y

'

%3

sec

(

tan

(

d

(

! sec

(

]

'

%3

! !3

y

2

!1

4

x

3

dx ! !

2

x

2

&

2

!1

!

3

2

y

1

!2

x

!4

dx !

x

!3

&

1

!2

! !

3

8

f !x" !

)

2

4 ! x

2

if !2 # x # 0

if 0

%

x # 2

y

2

!2

f !x" dx

f !x" !

)

sin x

cos x

if 0 # x

%

'

%2

if

'

%2 # x #

'

y

'

0

f !x" dx

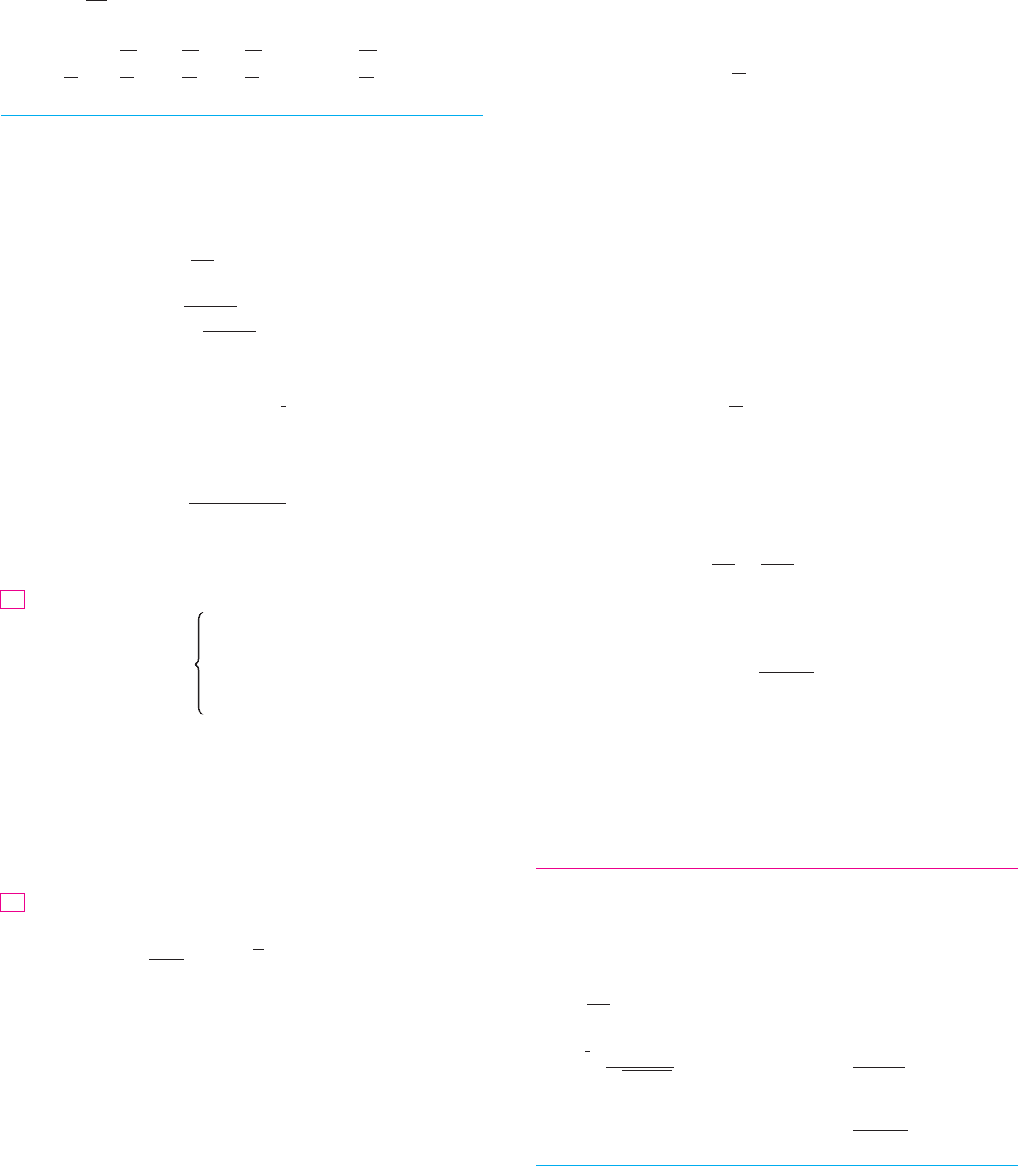
is overhauled, the company wants to determine the optimal

time (in months) between overhauls.

(a) Explain why represents the loss in value of the

machine over the period of time since the last overhaul.

(b) Let be given by

What does represent and why would the company want

to minimize ?

(c) Show that has a minimum value at the numbers

where .

68. A high-tech company purchases a new computing system

whose initial value is . The system will depreciate at the rate

and will accumulate maintenance costs at the rate

, where is the time measured in months. The com-

pany wants to determine the optimal time to replace the sys-

tem.

(a) Let

Show that the critical numbers of occur at the numbers

where .

(b) Suppose that

and

Determine the length of time for the total depreciation

to equal the initial value .

(c) Determine the absolute minimum of on .

(d) Sketch the graphs of and in the same coordinate

system, and verify the result in part (a) in this case.

The following exercises are intended only for those who have

already covered Chapter 7.

69–74 Evaluate the integral.

69. 70.

71. 72.

73. 74.

y

2

1

4 $ u

2

u

3

du

y

1

!1

e

u$1

du

y

1

0

4

t

2

$ 1

dt

y

s

3

%2

1%2

6

s

1 ! t

2

dt

y

1

0

10

x

dx

y

9

1

2x

dx

f $ tC

!0, T $C

VD!t" !

x

t

0

f !s" ds

T

t * 0t!t" !

Vt

2

12,900

f !t" !

)

0

V

15

!

V

450

t

if

0

%

t # 30

t * 30

C!t" ! f !t" $ t!t"t

C

C!t" !

1

t

y

t

0

# f !s" $ t!s"$ ds

tt ! t!t"

f ! f !t"

V

C!T" ! f !T "

t ! TC

C

C!t" !

1

t

(

A $

y

t

0

f !s" ds

&

C ! C!t"

t

x

t

0

f !s" ds

T

57– 58 Evaluate the limit by ﬁrst recognizing the sum as a

Riemann sum for a function deﬁned on .

57.

58.

59. Justify (3) for the case .

60. If is continuous and and are differentiable functions,

ﬁnd a formula for

61. (a) Show that for .

(b) Show that .

62. (a) Show that for .

(b) Deduce that .

63. Show that

by comparing the integrand to a simpler function.

Let

and

(a) Find an expression for similar to the one for .

(b) Sketch the graphs of and .

(c) Where is differentiable? Where is differentiable?

Find a function and a number such that

for all

66. Suppose h is a function such that , ,

, , , , and is continu-

ous everywhere. Evaluate .

67. A manufacturing company owns a major piece of equip-

ment that depreciates at the (continuous) rate , where

is the time measured in months since its last overhaul.

Because a ﬁxed cost is incurred each time the machine A

t

f ! f !t"

x

2

1

h)!u" du

h)h)!2" ! 13h"!2" ! 5h!2" ! 6h)!1" ! 3

h"!1" ! 2h!1" ! !2

x * 06 $

y

x

a

f !t"

t

2

dt ! 2

s

x

af

65.

tf

f !x"t!x"

t!x" !

y

x

0

f !t" dt

0

x

2 ! x

0

if x

%

0

if 0 # x # 1

if 1

%

x # 2

if x * 2

f !x" !

64.

0 #

y

10

5

x

2

x

4

$ x

2

$ 1

dx # 0.1

x

'

%6

0

cos!x

2

" dx &

1

2

0 # x # 1cos!x

2

" & cos x

1 #

x

1

0

s

1 $ x

3

dx # 1.25

x & 01 #

s

1 $ x

3

# 1 $ x

3

d

dx

y

h!x"

t!x"

f !t" dt

htf

h

%

0

lim

n l +

1

n

*

+

1

n

$

+

2

n

$

+

3

n

$ , , , $

+

n

,

lim

n l +

-

n

i!1

i

3

n

4

#0, 1$

SECTION 5.3 THE FUNDAMENTAL THEOREM OF CALCULUS

|| ||

323

IND EFI N ITE INT E GRA LS A N D TH E NE T CH A NGE THE ORE M

We saw in Section 5.3 that the second part of the Fundamental Theorem of Calculus pro-

vides a very powerful method for evaluating the deﬁnite integral of a function, assuming

that we can ﬁnd an antiderivative of the function. In this section we introduce a notation

for antiderivatives, review the formulas for antiderivatives, and use them to evaluate deﬁ-

nite integrals. We also reformulate FTC2 in a way that makes it easier to apply to science

and engineering problems.

INDEFINI T E IN T E G R A L S

Both parts of the Fundamental Theorem establish connections between antiderivatives and

deﬁnite integrals. Part 1 says that if is continuous, then is an antiderivative of .

Part 2 says that can be found by evaluating , where F is an antideriv-

ative of f.

We need a convenient notation for antiderivatives that makes them easy to work with.

Because of the relation given by the Fundamental Theorem between antiderivatives and

integrals, the notation is traditionally used for an antiderivative of and is called

an indeﬁnite integral. Thus

means

For example, we can write

So we can regard an indeﬁnite integral as representing an entire family of functions (one

antiderivative for each value of the constant C ).

|

You should distinguish carefully between deﬁnite and indeﬁnite integrals. A deﬁnite

integral is a number, whereas an indeﬁnite integral is a function (or

family of functions). The connection between them is given by Part 2 of the Fundamental

Theorem. If is continuous on , then

The effectiveness of the Fundamental Theorem depends on having a supply of anti-

derivatives of functions. We therefore restate the Table of Antidifferentiation Formulas

from Section 4.9, together with a few others, in the notation of indeﬁnite integrals. Any

formula can be veriﬁed by differentiating the function on the right side and obtaining the

integrand. For instance

because

d

dx

!tan x $ C" ! sec

2

x

y

sec

2

x dx ! tan x $ C

y

b

a

f !x" dx !

y

f !x" dx

]

a

b

#a, b$f

x f !x" dxx

b

a

f !x" dx

y

x

2

dx !

x

3

$ C because

d

dx

*

x

3

$ C

,

! x

2

F"!x" ! f !x"

y

f !x" dx ! F!x"

fx f !x" dx

F!b" ! F!a"x

b

a

f !x" dx

fx

x

a

f !t" dtf

5.4

324

|| ||

CHAPTER 5 INTEGRALS

TABLE OF INDEFINITE INTEGRALS

Recall from Theorem 4.9.1 that the most general antiderivative on a given interval is

obtained by adding a constant to a particular antiderivative. We adopt the convention that

when a formula for a general indeﬁnite integral is given, it is valid only on an inter-

val. Thus we write

with the understanding that it is valid on the interval or on the interval . This

is true despite the fact that the general antiderivative of the function , , is

EXAMPLE 1 Find the general indeﬁnite integral

SOLUTION Using our convention and Table 1, we have

You should check this answer by differentiating it. M

EXAMPLE 2 Evaluate .

SOLUTION This indeﬁnite integral isn’t immediately apparent in Table 1, so we use trigo-

nometric identities to rewrite the function before integrating:

M !

y

csc

(

cot

(

d

(

! !csc

(

$ C

y

cos

(

sin

2

(

d

(

!

y

*

1

sin

(

,*

cos

(

sin

(

,

d

(

y

cos

(

sin

2

(

d

(

V

! 2x

5

! 2 tan x $ C! 10

x

5

! 2 tan x $ C

y

!10x

4

! 2 sec

2

x" dx ! 10

y

x

4

dx ! 2

y

sec

2

x dx

y

!10x

4

! 2 sec

2

x" dx

!

1

x

$ C

2

if x * 0

F!x" !

!

1

x

$ C

1

if x

%

0

x " 0f !x" ! 1%x

2

!!+, 0"!0, +"

y

1

x

2

dx ! !

1

x

$ C

y

csc x cot x dx ! !csc x $ C

y

sec x tan x dx ! sec x $ C

y

csc

2

x dx ! !cot x $ C

y

sec

2

x dx ! tan x $ C

y

cos x dx ! sin x $ C

y

sin x dx ! !cos x $ C

!n " !1"

y

x

n

dx !

x

n$1

n $ 1

$ C

y

k dx ! kx $ C

y

# f !x" $ t!x"$ dx !

y

f !x" dx $

y

t!x" dx

y

cf !x" dx ! c

y

f !x" dx

1

SECTION 5.4 INDEFINITE INTEGRALS AND THE NET CHANGE THEOREM

|| ||

325

N The indeﬁnite integral in Example 1 is graphed

in Figure 1 for several values of . The value of

is the -intercept.

yC

C

4

_4

_1.5 1.5

FIG URE 1

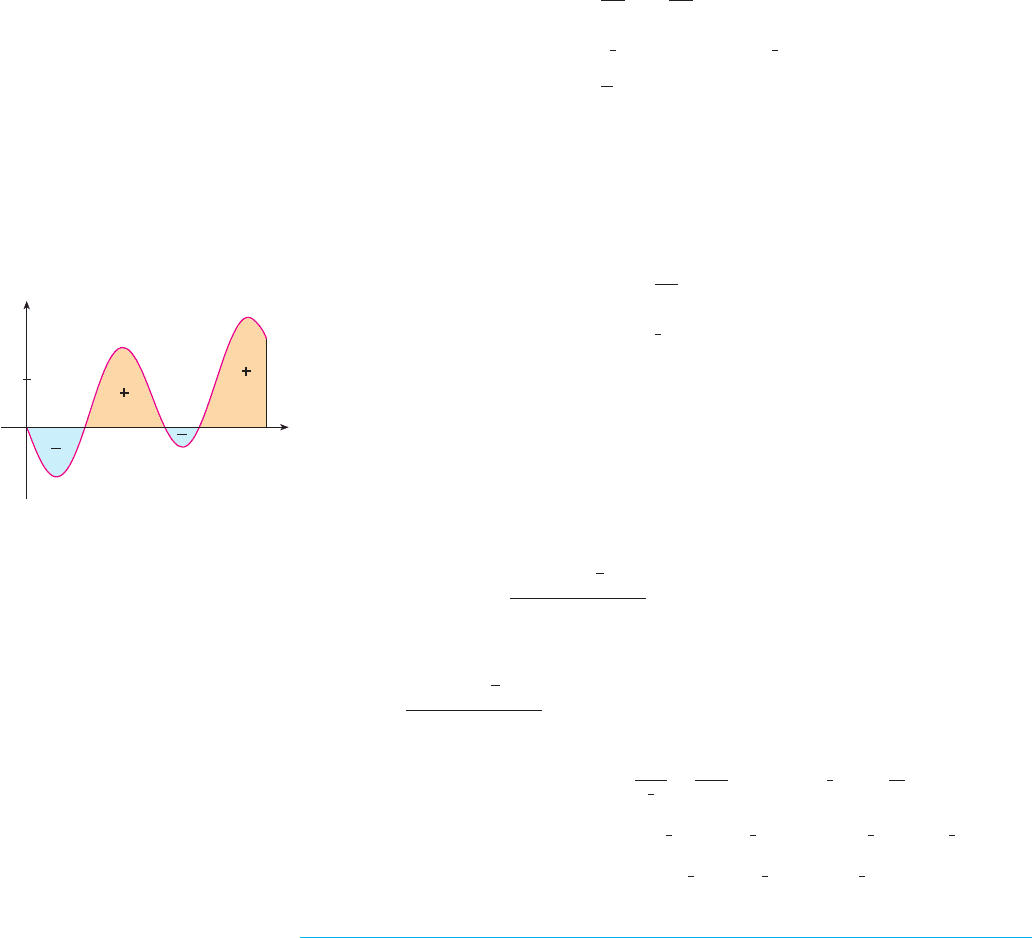
EXAMPLE 3 Evaluate .

SOLUTION Using FTC2 and Table 1, we have

Compare this calculation with Example 2(b) in Section 5.2. M

EXAMPLE 4 Find .

SOLUTION The Fundamental Theorem gives

This is the exact value of the integral. If a decimal approximation is desired, we can use

a calculator to approximate . Doing so, we get

M

EXAMPLE 5 Evaluate .

SOLUTION First we need to write the integrand in a simpler form by carrying out the

division:

M

APPLIC ATIONS

Part 2 of the Fundamental Theorem says that if f is continuous on , then

where F is any antiderivative of f. This means that , so the equation can be rewrit-

ten as

y

b

a

F"!x" dx ! F!b" ! F!a"

F" ! f

y

b

a

f !x" dx ! F!b" ! F!a"

#a, b$

! 18 $ 18 $

1

9

! 2 !

2

3

! 1 ! 32

4

9

!

(

2 ! 9 $

2

3

! 9

3%2

$

1

9

)

!

(

2 ! 1 $

2

3

! 1

3%2

$

1

)

! 2t $

2

3

t

3%2

$

1

t

&

1

9

! 2t $

t

3%2

3

2

!

t

!1

&

1

9

y

9

1

2t

2

$ t

2

s

t

! 1

t

2

dt !

y

9

1

!2 $ t

1%2

! t

!2

" dt

y

9

1

2t

2

$ t

2

s

t

! 1

t

2

dt

y

12

0

!x ! 12 sin x" dx . 70.1262

cos 12

! 60 $ 12 cos 12

! 72 $ 12 cos 12 ! 12

!

1

2

!12"

2

$ 12!cos 12 ! cos 0"

y

12

0

!x ! 12 sin x" dx !

x

2

! 12!!cos x"

&

0

12

y

12

0

!x ! 12 sin x" dx

!

81

4

! 27 ! 0 $ 0 ! !6.75

!

(

1

4

! 3

4

! 3 ! 3

2

)

!

(

1

4

! 0

4

! 3 ! 0

2

)

y

3

0

!x

3

! 6x" dx !

x

4

! 6

x

2

&

0

3

y

3

0

!x

3

! 6x" dx

326

|| ||

CHAPTER 5 INTEGRALS

N Figure 2 shows the graph of the integrand in

Example 4. We know from Section 5.2 that the

value of the integral can be interpreted as the

sum of the areas labeled with a plus sign minus

the areas labeled with a minus sign.

FIG URE 2

0

y

x

12

y=x-12sinx

10

We know that represents the rate of change of with respect to x and

is the change in y when x changes from a to b. [Note that could, for instance,

increase, then decrease, then increase again. Although might change in both directions,

represents the net change in .] So we can reformulate FTC2 in words as

follows.

THE NET CHANGE THEOREM The integral of a rate of change is the net change:

This principle can be applied to all of the rates of change in the natural and social sci-

ences that we discussed in Section 3.7. Here are a few instances of this idea:

N

If is the volume of water in a reservoir at time t, then its derivative is

the rate at which water ﬂows into the reservoir at time t. So

is the change in the amount of water in the reservoir between time and time .

N

If is the concentration of the product of a chemical reaction at time t, then

the rate of reaction is the derivative . So

is the change in the concentration of C from time to time .

N

If the mass of a rod measured from the left end to a point x is , then the

linear density is . So

is the mass of the segment of the rod that lies between and .

N

If the rate of growth of a population is , then

is the net change in population during the time period from to . (The popu-

lation increases when births happen and decreases when deaths occur. The net

change takes into account both births and deaths.)

N

If is the cost of producing x units of a commodity, then the marginal cost is

the derivative . So

is the increase in cost when production is increased from units to units.

N

If an object moves along a straight line with position function , then its

velocity is , so

y

t

2

t

1

v!t" dt ! s!t

2

" ! s!t

1

"

2

v!t" ! s"!t"

s!t"

x

2

x

1

y

x

2

x

1

C"!x" dx ! C!x

2

" ! C!x

1

"

C"!x"

C!x"

t

2

t

1

y

t

2

t

1

dn

dt

dt ! n!t

2

" ! n!t

1

"

dn%dt

x ! bx ! a

y

b

a

-

!x" dx ! m!b" ! m!a"

-

!x" ! m"!x"

m!x"

t

2

t

1

y

t

2

t

1

d#C$

dt

dt ! #C$!t

2

" ! #C$!t

1

"

d#C$%dt

#C$!t"

t

2

t

1

y

t

2

t

1

V"!t" dt ! V!t

2

" ! V!t

1

"

V"!t"V!t"

y

b

a

F"!x" dx ! F!b" ! F!a"

yF!b" ! F!a"

y

yF!b" ! F!a"

y ! F!x"F"!x"

SECTION 5.4 INDEFINITE INTEGRALS AND THE NET CHANGE THEOREM

|| ||

327

is the net change of position, or displacement, of the particle during the time

period from to . In Section 5.1 we guessed that this was true for the case

where the object moves in the positive direction, but now we have proved that it

is always true.

N

If we want to calculate the distance the object travels during that time interval,

we have to consider the intervals when (the particle moves to the right)

and also the intervals when (the particle moves to the left). In both cases

the distance is computed by integrating , the speed. Therefore

Figure 3 shows how both displacement and distance traveled can be interpreted

in terms of areas under a velocity curve.

N

The acceleration of the object is , so

is the change in velocity from time to time .

EXAMPLE 6 A particle moves along a line so that its velocity at time is

(measured in meters per second).

(a) Find the displacement of the particle during the time period .

(b) Find the distance traveled during this time period.

SOLUTION

(a) By Equation 2, the displacement is

This means that the particle moved 4.5 m toward the left.

(b) Note that and so on the interval

and on . Thus, from Equation 3, the distance traveled is

M

!

61

6

! 10.17 m

!

"

!

t

3

"

t

2

" 6t

#

3

1

"

t

3

!

t

2

! 6t

#

3

4

!

y

3

1

$!t

2

" t " 6% dt "

y

4

3

$t

2

! t ! 6% dt

y

4

1

&

v$t%

&

dt !

y

3

1

'!v$t%( dt "

y

4

3

v$t% dt

'3, 4(v$t% # 0

'1, 3(v$t% $ 0v$t% ! t

2

! t ! 6 ! $t ! 3%$t " 2%

!

"

t

3

!

t

2

! 6t

#

1

4

! !

9

2

s$4% ! s$1% !

y

4

1

v$t% dt !

y

4

1

$t

2

! t ! 6% dt

1 $ t $ 4

v$t% ! t

2

! t ! 6

t

V

t

2

t

1

y

t

2

t

1

a$t% dt ! v$t

2

% ! v$t

1

%

a$t% ! v%$t%

F I G U R E 3

t¡

t™

distance=

j 

|√(t)|dt=A¡+A™+A£

t¡

t™

displacement=

j 

√(t)dt=A¡-A™+A£

√

0

t

A¡

A™

A£

t¡ t™

√(t)

y

t

2

t

1

&

v$t%

&

dt ! total distance traveled

3

&

v$t%

&

v$t% $ 0

v$t% # 0

t

2

t

1

328

|| ||

CHAPTER 5 INTEGRALS

N To integrate the absolute value of , we use

Property 5 of integrals from Section 5.2 to split

the integral into two parts, one where

and one where .

v$t% # 0

v$t% $ 0

v$t%

EXAMPLE 7 Figure 4 shows the power consumption in the city of San Francisco for a

day in September (P is measured in megawatts; t is measured in hours starting at mid-

night). Estimate the energy used on that day.

SOLUTION Power is the rate of change of energy: . So, by the Net Change

Theorem,

is the total amount of energy used that day. We approximate the value of the integral

using the Midpoint Rule with 12 subintervals and :

The energy used was approximately 15,840 megawatt-hours. M

How did we know what units to use for energy in Example 7? The integral is

deﬁned as the limit of sums of terms of the form . Now is measured in

megawatts and is measured in hours, so their product is measured in megawatt-hours.

The same is true of the limit. In general, the unit of measurement for is the prod-

uct of the unit for and the unit for x.f $x%

x

b

a

f $x% dx

&t

P$t

i

*

%P$t

i

*

% &t

x

24

0

P$t% dt

! 15,840

" 840 " 810 " 690 " 670 " 550%$2%

! $440 " 400 " 420 " 620 " 790 " 840 " 850

y

24

0

P$t% dt ! 'P$1% " P$3% " P$5% " ' ' ' " P$21% " P$23%( &t

&t ! 2

y

24

0

P$t% dt !

y

24

0

E%$t% dt ! E$24% ! E$0%

P$t% ! E%$t%

F I G U R E 4

P

0

181512963

t

21

400

600

800

200

Pacific Gas & Electric

SECTION 5.4 INDEFINITE INTEGRALS AND THE NET CHANGE THEOREM

|| ||

329

N A note on units

5–16 Find the general indeﬁnite integral.

5. 6.

7. 8.

10.

11. 12.

y

)

u

2

" 1 "

1

u

2

*

du

y

x

3

! 2

s

x

dx

y

v$v

2

" 2%

2

dv

y

$1 ! t%$2 " t

2

% dt

9.

y

$y

3

" 1.8y

2

! 2.4y% dy

y

(

x

4

!

1

2

x

3

"

1

4

x ! 2

)

dx

y

(

s

x

3

"

s

3

x

2

)

dx

y

$x

2

" x

!2

%

dx

1– 4 Verify by differentiation that the formula is correct.

1.

3.

4.

y

x

s

a " bx

dx !

2

3b

2

$bx ! 2a%

s

a " bx

" C

y

cos

3

x dx ! sin x !

1

3

sin

3

x " C

y

x cos x dx ! x sin x " cos x " C

2.

y

x

s

x

2

" 1

dx !

s

x

2

" 1 " C

E X E R C I S E S

5.4

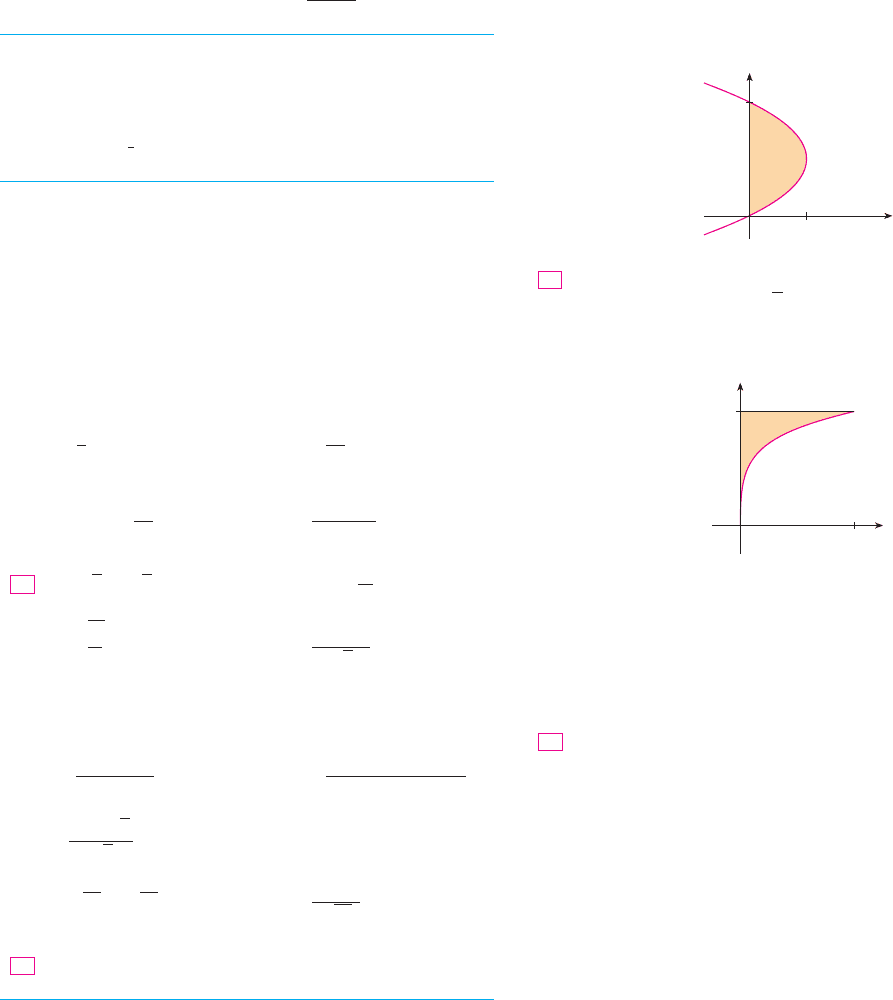
45. The area of the region that lies to the right of the -axis and

to the left of the parabola (the shaded region in

the ﬁgure) is given by the integral . (Turn your

head clockwise and think of the region as lying below the

curve from to .) Find the area of the

region.

The boundaries of the shaded region are the y-axis, the line

, and the curve . Find the area of this region by

writing x as a function of y and integrating with respect to y

(as in Exercise 45).

47. If is the rate of growth of a child in pounds per year,

what does represent?

48. The current in a wire is deﬁned as the derivative of the

charge: . (See Example 3 in Section 3.7.) What

does represent?

If oil leaks from a tank at a rate of gallons per minute at

time , what does represent?

50. A honeybee population starts with 100 bees and increases

at a rate of bees per week. What does

represent?

51. In Section 4.7 we deﬁned the marginal revenue function

as the derivative of the revenue function , where is the

number of units sold. What does represent?

52. If is the slope of a trail at a distance of miles from the

start of the trail, what does represent?

53. If is measured in meters and is measured in newtons,

what are the units for ?

54. If the units for are feet and the units for are pounds per

foot, what are the units for ? What units does

have?

x

8

2

a$x% dxda+dx

a$x%x

x

100

0

f $x% dx

f $x%x

x

5

3

f $x% dx

xf $x%

x

5000

1000

R%$x% dx

xR$x%

R%$x%

100 "

x

15

0

n%$t% dtn%$t%

x

120

0

r$t% dtt

r$t%

49.

x

b

a

I$t% dt

I$t% ! Q%$t%

x

10

5

w%$t% dt

w%$t%

y=$œ

„

x

y=1

0

y

x

1

y !

s

4

x

y ! 1

46.

0

y

x

1

x=2y-¥

2

y ! 2y ! 0x ! 2y ! y

2

x

2

0

$2y ! y

2

% dy

x ! 2y ! y

2

y

13. 14.

15. 16.

;

17–18 Find the general indeﬁnite integral. Illustrate by graphing

several members of the family on the same screen.

17. 18.

19– 42 Evaluate the integral.

19. 20.

21. 22.

23. 24.

25. 26.

27. 28.

30.

31. 32.

33. 34.

35. 36.

37. 38.

39. 40.

42.

;

43. Use a graph to estimate the -intercepts of the curve

. Then use this information to estimate the

area of the region that lies under the curve and above the

-axis.

;

44. Repeat Exercise 43 for the curve .y ! 2x " 3x

4

! 2x

6

x

y ! x " x

2

! x

4

x

y

3

(

+2

0

&

sin x

&

dx

y

2

!1

(

x ! 2

&

x

&

)

dx

41.

y

8

1

x ! 1

s

3

x

2

dx

y

1

0

(

s

4

x

5

"

s

5

x

4

)

dx

y

1

0

$1 " x

2

%

3

dx

y

64

1

1 "

s

3

x

s

x

dx

y

(

+3

0

sin

)

" sin

)

tan

2

)

sec

2

)

d

)

y

(

+4

0

1 " cos

2

)

cos

2

)

d

)

y

(

+3

(

+4

sec

)

tan

)

d

)

y

(

0

$4 sin

)

! 3 cos

)

%

d

)

y

9

1

3x ! 2

s

x

dx

y

4

1

,

5

x

dx

y

2

1

)

x "

1

x

*

2

dx

y

1

0

x

(

s

3

x

"

s

4

x

)

dx

29.

y

2

1

y " 5y

7

y

3

dy

y

!1

!2

)

4y

3

"

2

y

3

*

dy

y

9

0

s

2t

dt

y

4

1

s

t

$1 " t% dt

y

4

0

$2v " 5%$3v ! 1% dv

y

2

!2

$3u " 1%

2

du

y

0

!2

$u

5

! u

3

" u

2

% du

y

0

!3

$5y

4

! 6y

2

" 14% dy

y

3

1

$1 " 2x ! 4x

3

% dx

y

2

0

$6x

2

! 4x " 5% dx

y

$1 ! x

2

%

2

dx

y

(

cos x "

1

2

x

)

dx

y

sin 2x

sin x

dx

y

$1 " tan

2

*

%

d

*

y

sec t $sec t " tan t% dt

y

$

)

! csc

)

cot

)

%

d

)

330

|| ||

CHAPTER 5 INTEGRALS

yard). Find the increase in cost if the production level is raised

from 2000 yards to 4000 yards.

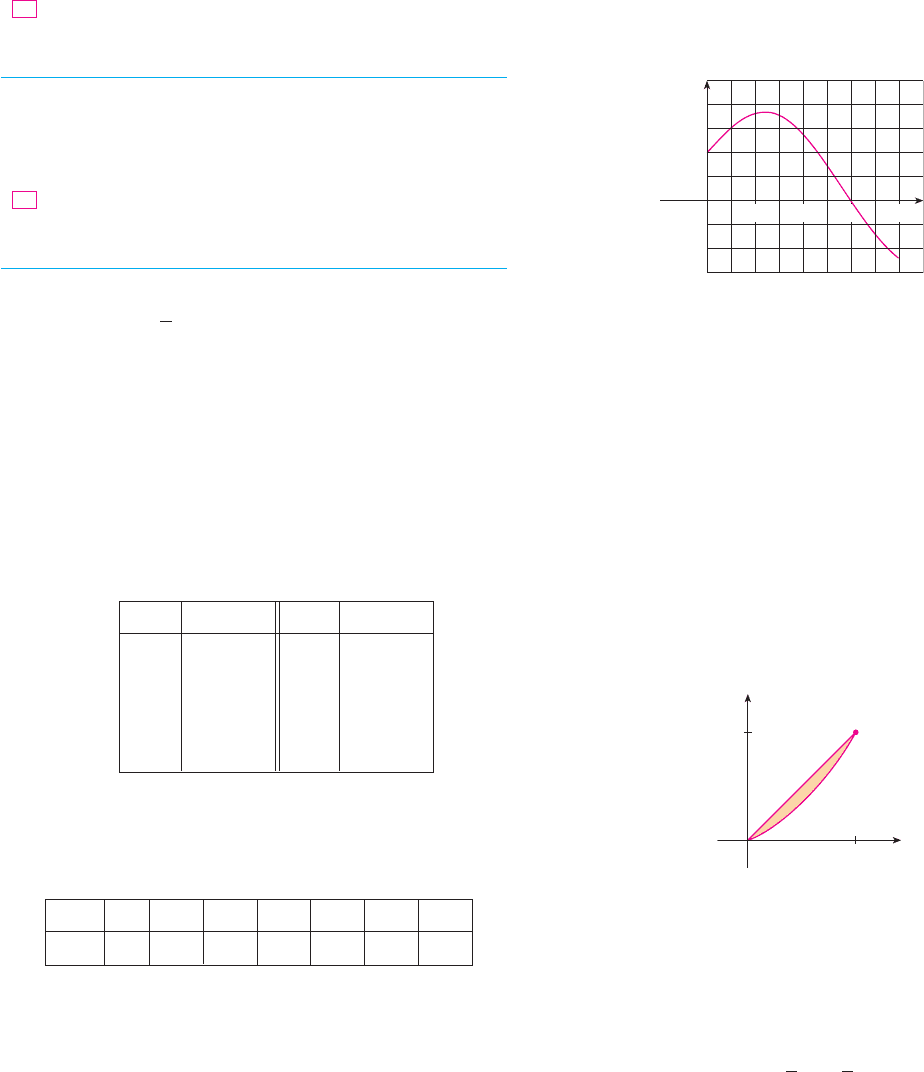
64. Water ﬂows into and out of a storage tank. A graph of the rate

of change of the volume of water in the tank, in liters per

day, is shown. If the amount of water in the tank at time

is 25,000 L, use the Midpoint Rule to estimate the amount of

water four days later.

65. Economists use a cumulative distribution called a Lorenz curve

to describe the distribution of income between households in a

given country. Typically, a Lorenz curve is deﬁned on

with endpoints and , and is continuous, increasing,

and concave upward. The points on this curve are determined

by ranking all households by income and then computing the

percentage of households whose income is less than or equal

to a given percentage of the total income of the country. For

example, the point is on the Lorenz curve if the

bottom of the households receive less than or equal to

of the total income. Absolute equality of income distribution

would occur if the bottom of the households receive of

the income, in which case the Lorenz curve would be the line

. The area between the Lorenz curve and the line

measures how much the income distribution differs from

absolute equality. The coefﬁcient of inequality is the ratio of

the area between the Lorenz curve and the line to the

area under .

(a) Show that the coefﬁcient of inequality is twice the area

between the Lorenz curve and the line , that is, show

that

(b) The income distribution for a certain country is represented

by the Lorenz curve deﬁned by the equation

What is the percentage of total income received by the

L$x% !

5

12

x

2

"

7

12

x

coefficient of inequality ! 2

y

1

0

'x ! L$x%( dx

y ! x

x

1

y

0

1

y=x

y=L(x)

(1,1)

y ! x

y ! xy ! x

a%a%

b%a%

$a+100, b+100%

$1, 1%$0, 0%

'0, 1(

3

2000

_1000

r

t

0

1 2 4

1000

t ! 0

r$t%

55–56 The velocity function (in meters per second) is given

for a particle moving along a line. Find (a) the displacement and

(b) the distance traveled by the particle during the given time

interval.

,

56. ,

57–58 The acceleration function (in m+s ) and the initial velocity

are given for a particle moving along a line. Find (a) the velocity at

time and (b) the distance traveled during the given time interval.

, ,

58. , ,

59. The linear density of a rod of length 4 m is given by

measured in kilograms per meter, where

is measured in meters from one end of the rod. Find the total

mass of the rod.

60. Water ﬂows from the bottom of a storage tank at a rate of

liters per minute, where . Find

the amount of water that ﬂows from the tank during the ﬁrst

10 minutes.

61. The velocity of a car was read from its speedometer at

10-second intervals and recorded in the table. Use the Mid-

point Rule to estimate the distance traveled by the car.

62. Suppose that a volcano is erupting and readings of the rate

at which solid materials are spewed into the atmosphere are

given in the table. The time is measured in seconds and the

units for are tonnes (metric tons) per second.

(a) Give upper and lower estimates for the total quantity

of erupted materials after 6 seconds.

(b) Use the Midpoint Rule to estimate .

63. The marginal cost of manufacturing yards of a certain

fabric is (in dollars per C%$x% ! 3 ! 0.01x " 0.000006x

2

x

Q$6%

r$t%

t

r$t%

0 $ t $ 50r$t% ! 200 ! 4t

x

+

$x% ! 9 " 2

s

x

0 $ t $ 3v $0% ! !4a$t% ! 2t " 3

0 $ t $ 10

v$0% ! 5a$t% ! t " 4

57.

t

2

1 $ t $ 6v$t% ! t

2

! 2t ! 8

0 $ t $ 3

v$t% ! 3t ! 5

55.

t (s) (mi+h) t (s) (mi+h)

0 0 60 56

10

38 70 53

20

52 80 50

30

58 90 47

40

55 100 45

5

0

51

vv

t 0 1 2 3 4 5 6

2 10 24 36 46 54 60r$t%

SECTION 5.4 INDEFINITE INTEGRALS AND THE NET CHANGE THEOREM

|| ||

331

Stewart J. Calculus

Подождите немного. Документ загружается.