Stewart J. Calculus
Подождите немного. Документ загружается.


and using Clairaut’s Theorem it can be shown that if these functions are
continuous.
EXAMPLE 7 Calculate if .
SOLUTION
M
PARTIAL DIFFERENTIAL EQUATIONS
Partial derivatives occur in partial differential equations that express certain physical laws.
For instance, the partial differential equation
is called Laplace’s equation after Pierre Laplace (1749–1827). Solutions of this equation
are called harmonic functions; they play a role in problems of heat conduction, fluid flow,
and electric potential.
EXAMPLE 8 Show that the function is a solution of Laplace’s
equation.
SOLUTION
Therefore satisfies Laplace’s equation. M
The wave equation
describes the motion of a waveform, which could be an ocean wave, a sound wave, a light
wave, or a wave traveling along a vibrating string. For instance, if represents the dis-
placement of a vibrating violin string at time and at a distance from one end of the
string (as in Figure 8), then satisfies the wave equation. Here the constant depends
on the density of the string and on the tension in the string.
EXAMPLE 9 Verify that the function satisfies the wave equation.
SOLUTION
So satisfies the wave equation. M
u
u
tt
苷 a
2
sin共x at兲 苷 a
2
u
xx
u
t
苷 a cos共x at兲
u
xx
苷 sin共x at兲 u
x
苷 cos共x at兲
u共x, t兲 苷 sin共x at兲
au共x, t兲
xt
u共x, t兲
2
u
t
2
苷 a
2
2
u
x
2
u
u
xx
u
yy
苷 e
x
sin y e
x
sin y 苷 0
u
yy
苷 e
x
sin y u
xx
苷 e
x
sin y
u
y
苷 e
x
cos y u
x
苷 e
x
sin y
u共x, y兲 苷 e
x
sin y
2
u
x
2
2
u
y
2
苷 0
f
xxyz
苷 9cos共3x y z兲 9yz sin共3x yz兲
f
xxy
苷 9z cos共3x yz兲
f
xx
苷 9sin共3x yz兲
f
x
苷 3cos共3x yz兲
f 共x, y, z兲 苷 sin共3x yz兲f
xxyz
V
f
xyy
苷 f
yxy
苷 f
yyx
922
||||
CHAPTER 15 PARTIAL DERIVATIVES
FIGURE 8
u(x,t)
x
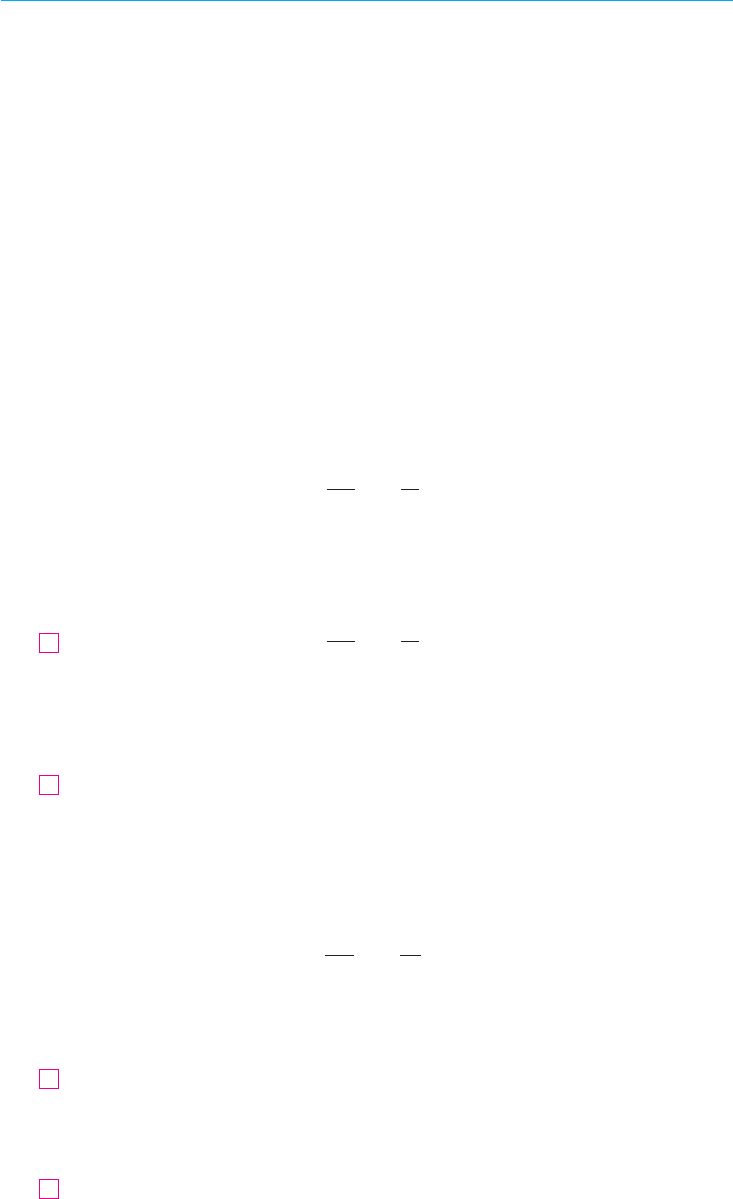
THE COBB-DOUGLAS PRODUCTION FUNCTION
In Example 3 in Section 15.1 we described the work of Cobb and Douglas in modeling the
total production P of an economic system as a function of the amount of labor L and the
capital investment K. Here we use partial derivatives to show how the particular form of
their model follows from certain assumptions they made about the economy.
If the production function is denoted by , then the partial derivative
is the rate at which production changes with respect to the amount of labor. Economists
call it the marginal production with respect to labor or the marginal productivity of labor.
Likewise, the partial derivative is the rate of change of production with respect to
capital and is called the marginal productivity of capital. In these terms, the assumptions
made by Cobb and Douglas can be stated as follows.
(i) If either labor or capital vanishes, then so will production.
(ii) The marginal productivity of labor is proportional to the amount of production
per unit of labor.
(iii) The marginal productivity of capital is proportional to the amount of production
per unit of capital.
Because the production per unit of labor is , assumption (ii) says that
for some constant . If we keep K constant , then this partial differential equa-
tion becomes an ordinary differential equation:
If we solve this separable differential equation by the methods of Section 10.3 (see also
Exercise 79), we get
Notice that we have written the constant as a function of because it could depend on
the value of .
Similarly, assumption (iii) says that
and we can solve this differential equation to get
Comparing Equations 6 and 7, we have
P共L, K兲 苷 bL
K
8
P共L
0
, K兲 苷 C
2
共L
0
兲K
7
P
K
苷
P
K
K
0
K
0
C
1
P共L, K
0
兲 苷 C
1
共K
0
兲L
6
dP
dL
苷
P
L
5
共K 苷 K
0
兲
P
L
苷
P
L
P兾L
P兾K
P兾LP 苷 P共L, K兲
SECTION 15.3 PARTIAL DERIVATIVES
||||
923
where b is a constant that is independent of both L and K. Assumption (i) shows that
and .
Notice from Equation 8 that if labor and capital are both increased by a factor m, then
If , then , which means that production is also increased
by a factor of m. That is why Cobb and Douglas assumed that and therefore
This is the Cobb-Douglas production function that we discussed in Section 15.1.
P共L, K兲 苷 bL
K
1
苷 1
P共mL, mK兲 苷 mP共L, K 兲
苷 1
P共mL, mK兲 苷 b共mL兲
共mK兲
苷 m
bL
K
苷 m
P共L, K兲
0
0
924
||||
CHAPTER 15 PARTIAL DERIVATIVES
(b) In general, what can you say about the signs of
and ?
(c) What appears to be the value of the following limit?
4.
The wave heights in the open sea depend on the speed
of the wind and the length of time that the wind has been
blowing at that speed. Values of the function are
recorded in feet in the following table.
(a) What are the meanings of the partial derivatives
and ?
(b) Estimate the values of and . What are
the practical interpretations of these values?
(c) What appears to be the value of the following limit?
lim
t
l
h
t
f
t
共40, 15兲f
v
共40, 15兲
h兾t
h兾
v
2
4
5
9
14
19
24
2
4
7
13
21
29
37
2
5
8
16
25
36
47
2
5
8
17
28
40
54
2
5
9
18
31
45
62
2
5
9
19
33
48
67
2
5
9
19
33
50
69
v
t
10
15
20
30
40
50
60
Duration (hours)
Wind speed (knots)
5
10 15
20 30
40
50
h 苷 f 共
v
, t兲
t
v
h
lim
v
l
W
v
W兾v
W兾TThe temperature at a location in the Northern Hemisphere
depends on the longitude , latitude , and time , so we can
write . Let’s measure time in hours from the
beginning of January.
(a) What are the meanings of the partial derivatives
, and ?
(b) Honolulu has longitude and latitude .
Suppose that at 9:00
AM
on January 1 the wind is blowing
hot air to the northeast, so the air to the west and south is
warm and the air to the north and east is cooler. Would you
expect , and to be
positive or negative? Explain.
2.
At the beginning of this section we discussed the function
, where is the heat index, is the temperature,
and is the relative humidity. Use Table 1 to estimate
and . What are the practical interpretations
of these values?
3.
The wind-chill index is the perceived temperature when the
actual temperature is and the wind speed is , so we can
write . The following table of values is an excerpt
from Table 1 in Section 15.1.
(a) Estimate the values of and . What
are the practical interpretations of these values?
f
v
共15, 30兲f
T
共15, 30兲
18
24
30
37
20
26
33
39
21
27
34
41
22
29
35
42
23
30
36
43
T
v
20 30 40 50 60
10
15
20
25
Actual temperature (°C)
70
23
30
37
44
Wind speed (km/h)
W 苷 f 共T,
v
兲
v
T
W
f
H
共92, 60兲f
T
共92, 60兲
H
TII 苷 f 共T, H兲
f
t
共158, 21, 9兲f
x
共158, 21, 9兲, f
y
共158, 21, 9兲
21 N158 W
T兾tT兾y
T兾x,
T 苷 f 共x, y, t兲
tyx
T
1.
EXERCISES
15.3
Openmirrors.com
SECTION 15.3 PARTIAL DERIVATIVES
||||
925
10. A contour map is given for a function . Use it to estimate
and .
11. If , find and and inter-
pret these numbers as slopes. Illustrate with either hand-drawn
sketches or computer plots.
12. If , find and and
interpret these numbers as slopes. Illustrate with either hand-
drawn sketches or computer plots.
;
13–14 Find and and graph , , and with domains and
viewpoints that enable you to see the relationships between them.
13. 14.
15–38 Find the first partial derivatives of the function.
15. 16.
17. 18.
19. 20.
22.
23. 24.
25. 26.
27. 28.
29. 30.
32.
33. 34.
35. 36.
37.
38.
39– 42 Find the indicated partial derivatives.
39. ;
40. ;
41. ; f
y
共2, 1, 1兲f 共x, y, z兲 苷
y
x y z
f
x
共2, 3兲f 共x, y兲 苷 arctan共y兾x兲
f
x
共3, 4兲f 共x, y兲 苷 ln
(
x
s
x
2
y
2
)
u 苷 sin共x
1
2x
2
nx
n
兲
u 苷
s
x
2
1
x
2
2
x
2
n
f 共x, y, z, t兲 苷
xy
2
t 2z
f 共x, y, z, t兲 苷 xyz
2
tan共yt兲
u 苷 x
y兾z
u 苷 xy sin
1
共yz兲
w 苷 ze
xyz
w 苷 ln共x 2y 3z兲
31.
f 共x, y, z兲 苷 x sin共y z兲f 共x, y, z兲 苷 xz 5x
2
y
3
z
4
f 共x, y兲 苷
y
x
y
cos共t
2
兲 dtu 苷 te
w兾t
f 共x, t兲 苷 arctan
(
x
s
t
)
f 共r, s兲 苷 r ln共r
2
s
2
兲
w 苷 e
v
兾共u v
2
兲w 苷 sin
cos
f 共x, y兲 苷 x
y
f 共x, y兲 苷
x y
x y
21.
z 苷 tan xyz 苷 共2x 3y兲
10
f 共x, t兲 苷
s
x
ln tf 共x, t兲 苷 e
t
cos
x
f 共x, y兲 苷 x
4
y
3
8x
2
yf 共x, y兲 苷 y
5
3xy
f 共x, y兲 苷 xe
x
2
y
2
f 共x, y兲 苷 x
2
y
2
x
2
y
f
y
f
x
ff
y
f
x
f
y
共1, 0兲f
x
共1, 0兲f 共x, y兲 苷
s
4 x
2
4y
2
f
y
共1, 2兲f
x
共1, 2兲f 共x, y兲 苷 16 4x
2
y
2
3
x
y
3
_2
0
6
8
10
14
16
12
18
2
4
_4
1
f
y
共2, 1兲f
x
共2, 1兲
f
5–8 Determine the signs of the partial derivatives for the function
whose graph is shown.
(a) (b)
6. (a) (b)
7. (a) (b)
8. (a) (b)
The following surfaces, labeled , , and , are graphs of a
function and its partial derivatives and . Identify each
surface and give reasons for your choices.
b
_4
_3
_1
0
1
3
0
_2
y
x
z
0
2
4
2
_2
a
8
_8
_4
_3
_1
0
1
3
0
_2
y
x
z
0
2
4
2
_2
c
8
_8
_3
_1
0
1
3
0
_2
y
x
z
0
2
4
2
_2
_4
f
y
f
x
f
cba
9.
f
xy
共1, 2兲f
xy
共1, 2兲
f
yy
共1, 2兲f
xx
共1, 2兲
f
y
共1, 2兲f
x
共1, 2兲
f
y
共1, 2兲f
x
共1, 2兲
5.
1
x
y
z
2
f

926
||||
CHAPTER 15 PARTIAL DERIVATIVES
Use the table of values of to estimate the values of
, , and .
70. Level curves are shown for a function . Determine whether
the following partial derivatives are positive or negative at the
point .
(a) (b) (c)
(d) (e)
71. Verify that the function is a solution of the
heat conduction equation .
72. Determine whether each of the following functions is a solution
of Laplace’s equation .
(a) (b)
(c) (d)
(e)
(f)
73. Verify that the function is a solution of
the three-dimensional Laplace equation .
74. Show that each of the following functions is a solution of the
wave equation .
(a) (b)
(c)
(d)
75. If and are twice differentiable functions of a single vari-
able, show that the function
is a solution of the wave equation given in Exercise 74.
76. If , where ,
show that
77. Verify that the function is a solution of the
differential equations
z
x
z
y
苷 1
z 苷 ln共e
x
e
y
兲
2
u
x
2
1
2
u
x
2
2
2
u
x
2
n
苷 u
a
2
1
a
2
2
a
2
n
苷 1u 苷 e
a
1
x
1
a
2
x
2
a
n
x
n
u共x, t兲 苷 f 共x at兲 t共x at兲
tf
u 苷 sin共x at兲 ln共x at兲
u 苷 共x at兲
6
共x at兲
6
u 苷 t兾共a
2
t
2
x
2
兲u 苷 sin共kx兲 sin共akt兲
u
tt
苷 a
2
u
xx
u
xx
u
yy
u
zz
苷 0
u 苷 1兾
s
x
2
y
2
z
2
u 苷 e
x
cos y e
y
cos x
u 苷 sin x cosh y cos x sinh y
u 苷 ln
s
x
2
y
2
u 苷 x
3
3xy
2
u 苷 x
2
y
2
u 苷 x
2
y
2
u
xx
u
yy
苷 0
u
t
苷
2
u
xx
u 苷 e
2
k
2
t
sin kx
10
8
6
4
2
y
x
P
f
yy
f
xy
f
xx
f
y
f
x
P
f
12.5
18.1
20.0
10.2
17.5
22.4
9.3
15.9
26.1
x
y
2.5
3.0
3.5
1.8 2.0 2.2
f
xy
共3, 2兲f
x
共3, 2.2兲f
x
共3, 2兲
f 共x, y兲
69.
42. ;
43– 44 Use the definition of partial derivatives as limits (4) to find
and .
43. 44.
45– 48 Use implicit differentiation to find and .
45. 46.
47. 48.
49–50 Find and .
49. (a) (b)
(a) (b)
(c)
51–56 Find all the second partial derivatives.
51. 52.
53. 54.
55. 56.
57–60 Verify that the conclusion of Clairaut’s Theorem holds, that
is, .
57. 58.
59. 60.
61–68 Find the indicated partial derivative.
61. ;,
62. ;,
63. ;,
64. ;,
65. ;
66.
;
67. ;,
68. ;
6
u
x y
2
z
3
u 苷 x
a
y
b
z
c
3
w
x
2
y
3
w
z y x
w 苷
x
y 2z
3
z
u v w
z 苷 u
s
v w
3
u
r
2
u 苷 e
r
sin
f
rst
f
rss
f 共r, s, t兲 苷 r ln共rs
2
t
3
兲
f
yzz
f
xyz
f 共x, y, z兲 苷 cos共4x 3y 2z兲
f
txx
f
ttt
f 共x, t兲 苷 x
2
e
ct
f
yyy
f
xxy
f 共x, y兲 苷 3xy
4
x
3
y
2
u 苷 xye
y
u 苷 ln
s
x
2
y
2
u 苷 x
4
y
2
2xy
5
u 苷 x sin共x 2y兲
u
xy
苷 u
yx
v 苷 e
xe
y
z 苷 arctan
x y
1 xy
v 苷
xy
x y
w 苷
s
u
2
v
2
f 共x, y兲 苷 sin
2
共mx ny兲f 共x, y兲 苷 x
3
y
5
2x
4
y
z 苷 f 共x兾y兲
z 苷 f 共xy兲z 苷 f 共x兲t共y兲
50.
z 苷 f 共x y兲z 苷 f 共x兲 t共y兲
z兾yz兾x
sin共xyz兲 苷 x 2y 3zx z 苷 arctan共yz兲
yz 苷 ln共x z兲x
2
y
2
z
2
苷 3xyz
z兾yz兾x
f 共x, y兲 苷
x
x y
2
f 共x, y兲 苷 xy
2
x
3
y
f
y
共x, y兲f
x
共x, y兲
f
z
共0, 0,
兾4兲f 共x, y, z兲 苷
s
sin
2
x sin
2
y sin
2
z

SECTION 15.3 PARTIAL DERIVATIVES
||||
927
You are told that there is a function whose partial derivatives
are and . Should you
believe it?
;
88. The paraboloid intersects the plane
in a parabola. Find parametric equations for the tangent
line to this parabola at the point . Use a computer to
graph the paraboloid, the parabola, and the tangent line on the
same screen.
89. The ellipsoid intersects the plane
in an ellipse. Find parametric equations for the tangent line to
this ellipse at the point .
90. In a study of frost penetration it was found that the temperature
at time (measured in days) at a depth (measured in feet)
can be modeled by the function
where and is a positive constant.
(a) Find . What is its physical significance?
(b) Find . What is its physical significance?
(c) Show that satisfies the heat equation for a cer-
tain constant .
;
(d) If , , and , use a computer to
graph .
(e) What is the physical significance of the term in the
expression ?
91. Use Clairaut’s Theorem to show that if the third-order partial
derivatives of are continuous, then
92. (a) How many th-order partial derivatives does a function of
two variables have?
(b) If these partial derivatives are all continuous, how many of
them can be distinct?
(c) Answer the question in part (a) for a function of three
variables.
93. If , find .
[Hint: Instead of finding first, note that it’s easier to
use Equation 1 or Equation 2.]
94. If , find .
95. Let
;
(a) Use a computer to graph .
(b) Find and when .
(c) Find and using Equations 2 and 3.
(d) Show that and .
(e) Does the result of part (d) contradict Clairaut’s Theorem?
Use graphs of and to illustrate your answer.f
yx
f
xy
CAS
f
yx
共0, 0兲 苷 1f
xy
共0, 0兲 苷 1
f
y
共0, 0兲f
x
共0, 0兲
共x, y兲 苷 共0, 0兲f
y
共x, y兲f
x
共x, y兲
f
f 共x, y兲 苷
再
0
x
3
y xy
3
x
2
y
2
if
if
共x, y兲 苷 共0, 0兲
共x, y兲 苷 共0, 0兲
f
x
共0, 0兲
f 共x, y兲 苷
s
3
x
3
y
3
f
x
共x, y兲
f
x
共1, 0兲f 共x, y兲 苷 x共x
2
y
2
兲
3兾2
e
sin共x
2
y兲
n
f
xyy
苷 f
yxy
苷 f
yyx
f
sin共
t
x兲
x
T共x, t兲
T
1
苷 10T
0
苷 0
苷 0.2
k
T
t
苷 kT
xx
T
T兾t
T兾x
苷 2
兾365
T共x, t兲 苷 T
0
T
1
e
x
sin共
t
x兲
xtT
共1, 2, 2兲
y 苷 24x
2
2y
2
z
2
苷 16
共1, 2, 4兲
x 苷 1
z 苷 6 x x
2
2y
2
f
y
共x, y兲 苷 3x yf
x
共x, y兲 苷 x 4y
f
87.
and
78. Show that the Cobb-Douglas production function
satisfies the equation
79. Show that the Cobb-Douglas production function satisfies
by solving the differential equation
(See Equation 5.)
80. The temperature at a point on a flat metal plate is given
by , where is measured in C
and in meters. Find the rate of change of temperature with
respect to distance at the point in (a) the -direction and
(b) the -direction.
The total resistance produced by three conductors with resis-
tances , , connected in a parallel electrical circuit is
given by the formula
Find .
82. The gas law for a fixed mass of an ideal gas at absolute tem-
perature , pressure , and volume is , where is
the gas constant. Show that
83. For the ideal gas of Exercise 82, show that
84. The wind-chill index is modeled by the function
where is the temperature and is the wind speed
. When and , by how much
would you expect the apparent temperature to drop if the
actual temperature decreases by ? What if the wind speed
increases by ?
85. The kinetic energy of a body with mass and velocity is
. Show that
If , , are the sides of a triangle and , , are the opposite
angles, find , , by implicit differentiation of
the Law of Cosines.
A兾cA兾bA兾a
CBAcba
86.
K
m
2
K
v
2
苷 K
K 苷
1
2
mv
2
vm
1 km兾h
1C
W
v 苷 30 km兾hT 苷 15C共km兾h兲
v共C兲T
W 苷 13.12 0.6215T 11.37v
0.16
0.3965Tv
0.16
T
P
T
V
T
苷 mR
P
V
V
T
T
P
苷 1
RPV 苷 mRTVPT
m
R兾R
1
1
R
苷
1
R
1
1
R
2
1
R
3
R
3
R
2
R
1
R
81.
y
x共2, 1兲
x, y
TT共x, y兲 苷 60兾共1 x
2
y
2
兲
共x, y兲
dP
dL
苷
P
L
P共L, K
0
兲 苷 C
1
共K
0
兲L
L
P
L
K
P
K
苷 共
兲P
P 苷 bL
K
2
z
x
2
2
z
y
2
冉
2
z
x y
冊
2
苷 0
928
||||
CHAPTER 15 PARTIAL DERIVATIVES
TANGENT PLANES AND LINEAR APPROXIMATIONS
One of the most important ideas in single-variable calculus is that as we zoom in toward a
point on the graph of a differentiable function, the graph becomes indistinguishable from
its tangent line and we can approximate the function by a linear function. (See Sec-
tion 3.9.) Here we develop similar ideas in three dimensions. As we zoom in toward a point
on a surface that is the graph of a differentiable function of two variables, the surface looks
more and more like a plane (its tangent plane) and we can approximate the function by a
linear function of two variables. We also extend the idea of a differential to functions of
two or more variables.
TANGENT PLANES
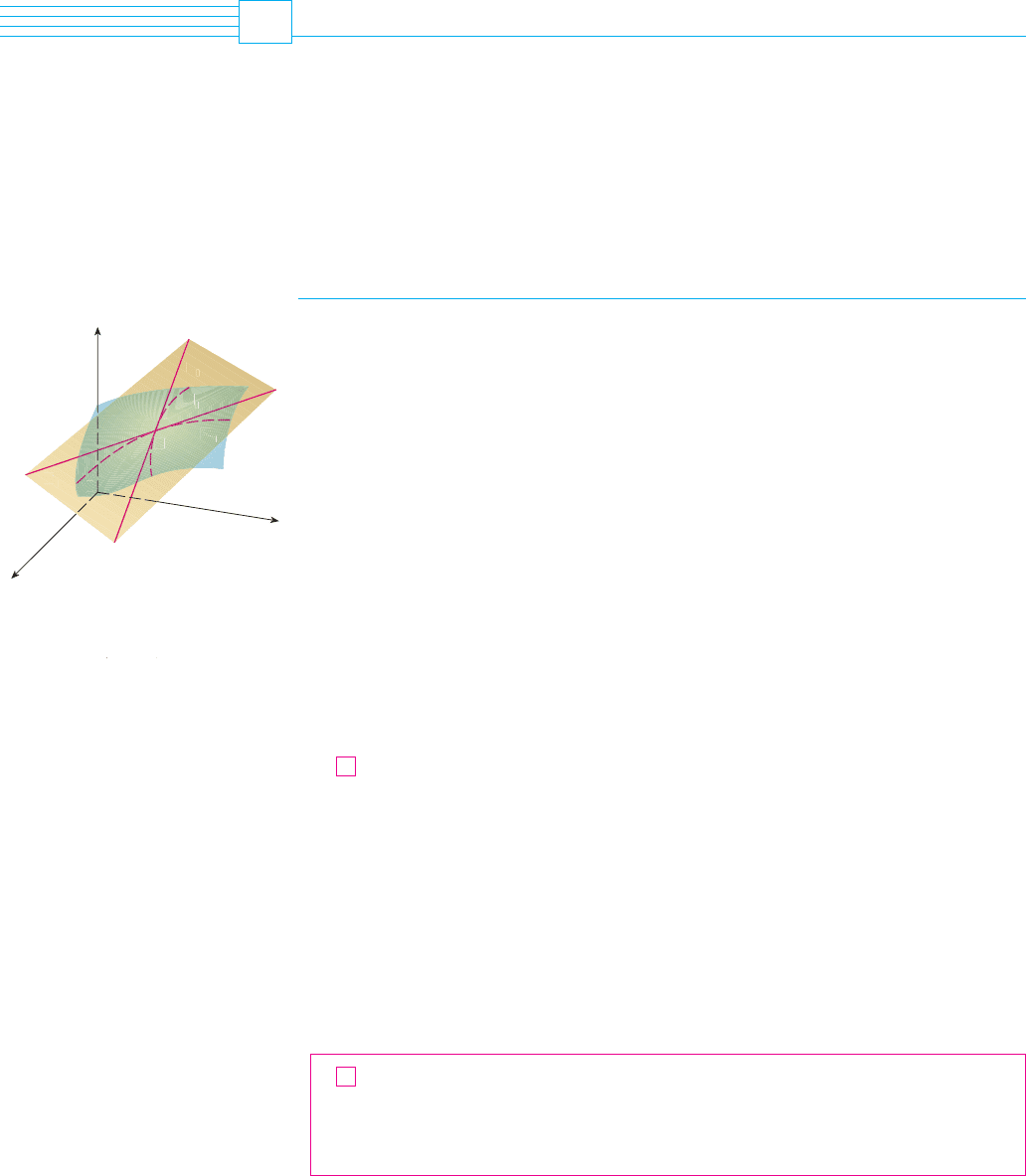
Suppose a surface has equation , where has continuous first partial deriva-
tives, and let be a point on . As in the preceding section, let and be the
curves obtained by intersecting the vertical planes and with the surface .
Then the point lies on both and . Let and be the tangent lines to the curves
and at the point . Then the tangent plane to the surface at the point is defined to
be the plane that contains both tangent lines and . (See Figure 1.)
We will see in Section 15.6 that if is any other curve that lies on the surface and
passes through , then its tangent line at also lies in the tangent plane. Therefore you
can think of the tangent plane to at as consisting of all possible tangent lines at to
curves that lie on and pass through . The tangent plane at is the plane that most
closely approximates the surface near the point .
We know from Equation 13.5.7 that any plane passing through the point has
an equation of the form
By dividing this equation by and letting and , we can write it in
the form
If Equation 1 represents the tangent plane at , then its intersection with the plane
must be the tangent line . Setting in Equation 1 gives
and we recognize these as the equations (in point-slope form) of a line with slope .
But from Section 15.3 we know that the slope of the tangent is . Therefore
.
Similarly, putting in Equation 1, we get , which must repre-
sent the tangent line , so .
Suppose has continuous partial derivatives. An equation of the tangent plane
to the surface at the point is
z z
0
苷 f
x
共x
0
, y
0
兲共x x
0
兲 f
y
共x
0
, y
0
兲共y y
0
兲
P共x
0
, y
0
, z
0
兲z 苷 f 共x, y兲
f
2
b 苷 f
y
共x
0
, y
0
兲T
2
z z
0
苷 b共y y
0
兲x 苷 x
0
a 苷 f
x
共x
0
, y
0
兲
f
x
共x
0
, y
0
兲T
1
a
y 苷 y
0
z z
0
苷 a共x x
0
兲
y 苷 y
0
T
1
y 苷 y
0
P
z z
0
苷 a共x x
0
兲 b共y y
0
兲
1
b 苷 B兾Ca 苷 A兾CC
A共x x
0
兲 B共y y
0
兲 C共z z
0
兲 苷 0
P共x
0
, y
0
, z
0
兲
PS
PPS
PPS
PP
SC
T
2
T
1
PSPC
2
C
1
T
2
T
1
C
2
C
1
P
Sx 苷 x
0
y 苷 y
0
C
2
C
1
SP共x
0
, y
0
, z
0
兲
fz 苷 f 共x, y兲S
15.4
FI
G
URE
1
T
h
e tangent p
l
ane conta
i
ns t
he
tangent lines
T
¡
TT
and
T
™
TT
.
y
x
z
T
T
T
T
T
¡
¡
¡
T
T
T
T
T
™
™
™
C
C
C
C
C
C
C
C
C
C
C
C
C
C
C
C
C
C
C
C
C
C
C
C
C
C
C
C
C
C
C
¡
¡
¡
¡
¡
¡
¡
C
C
C
C
C
C
C
C
C
C
C
C
C
C
C
C
C
C
C
C
C
C
™
™
™
™
™
™
™
™
™
™
™
™
™
P
P
P
P
P
P
P
P
P
P
P
P
P
P
P
P
P
P
P
P
P
0
0
0
0
0
0
0
0
0
0
0
0
N Note the similarity between the equation of a
tangent plane and the equation of a tangent line:
y y
0
苷 f 共x
0
兲共x x
0
兲
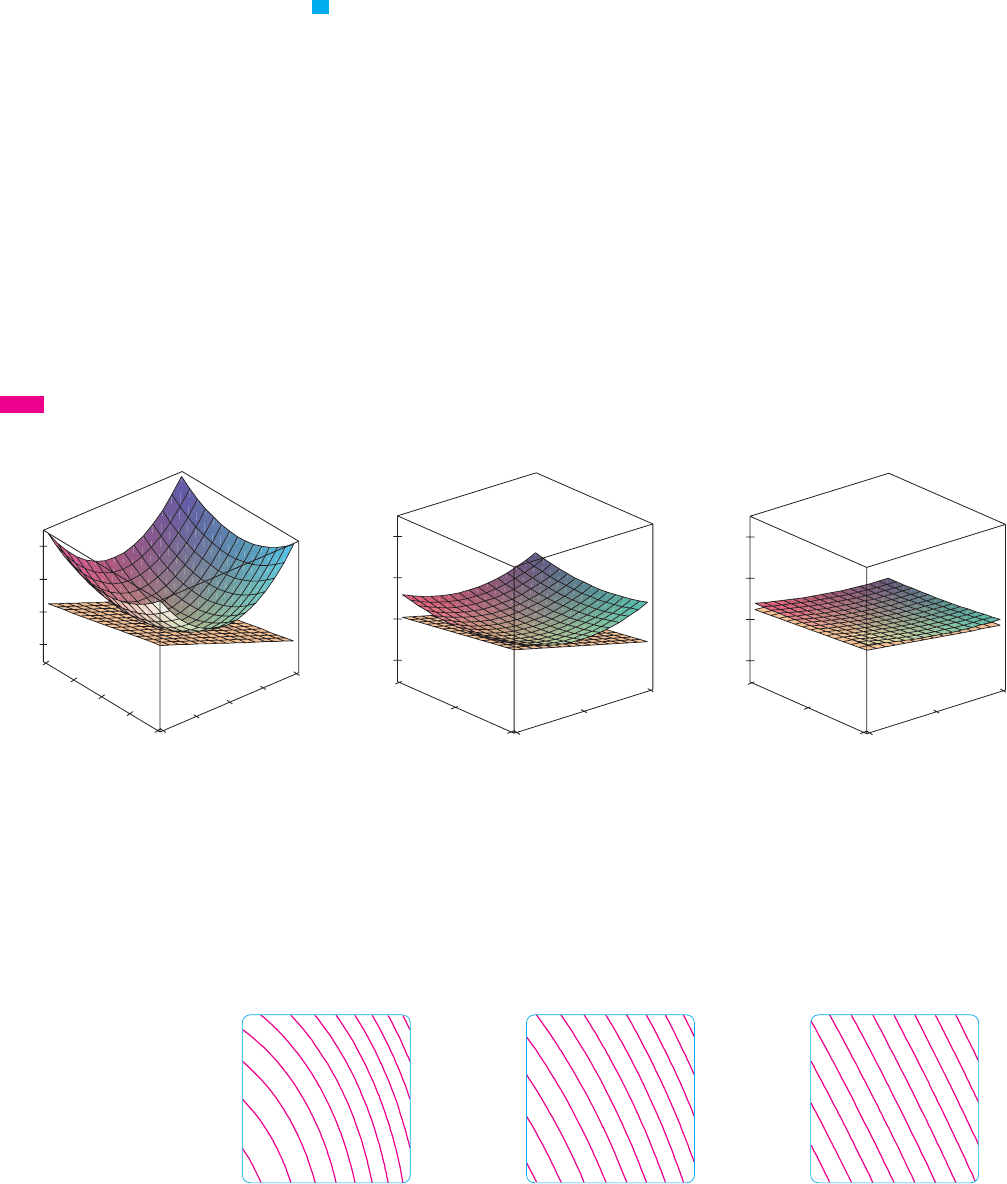
EXAMPLE 1 Find the tangent plane to the elliptic paraboloid at the
point .
SOLUTION Let . Then
Then (2) gives the equation of the tangent plane at as
or M
Figure 2(a) shows the elliptic paraboloid and its tangent plane at that we found
in Example 1. In parts (b) and (c) we zoom in toward the point by restricting the
domain of the function . Notice that the more we zoom in, the flatter
the graph appears and the more it resembles its tangent plane.
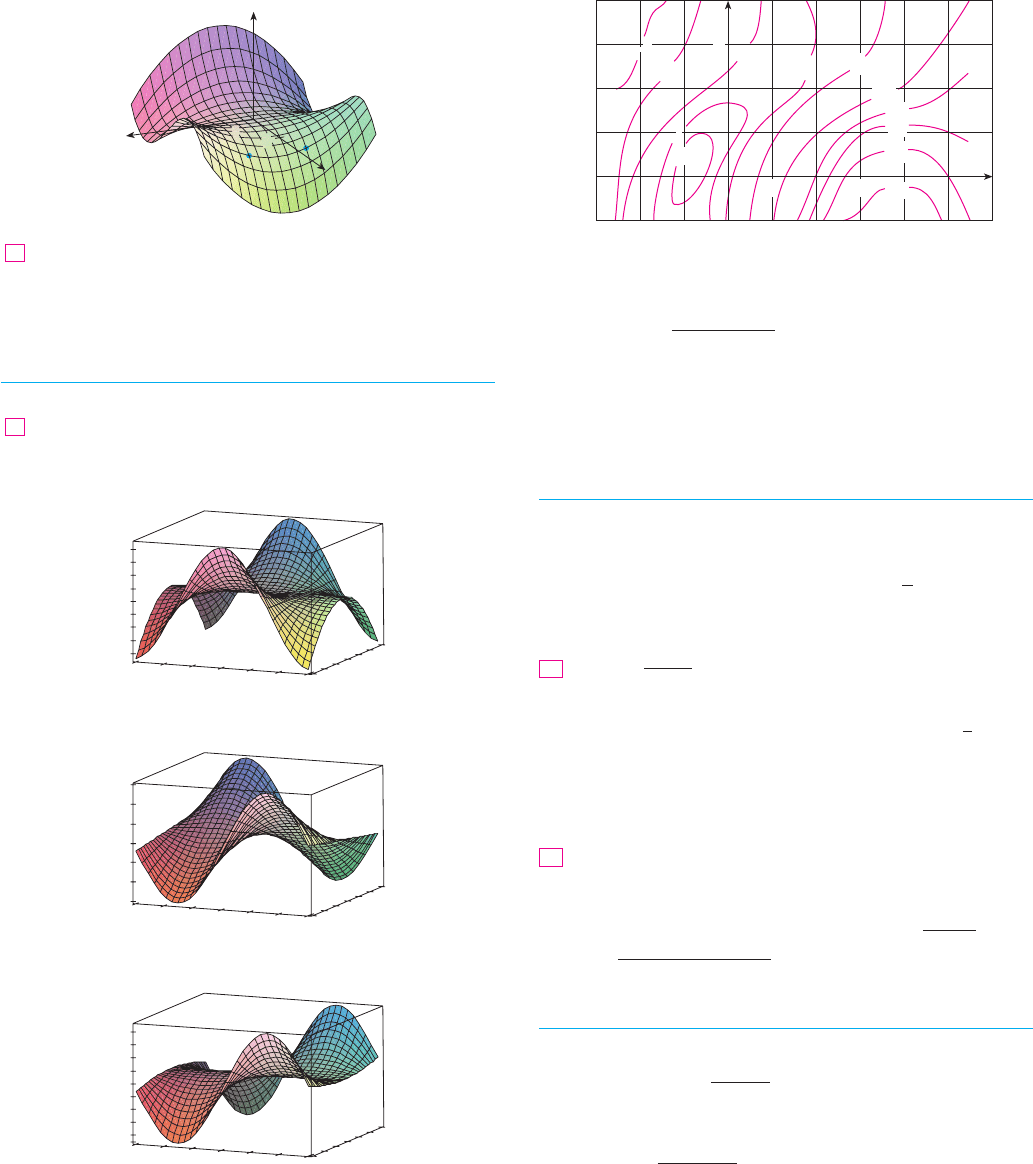
In Figure 3 we corroborate this impression by zooming in toward the point on a
contour map of the function . Notice that the more we zoom in, the
more the level curves look like equally spaced parallel lines, which is characteristic of a
plane.
FIGURE 3
Zooming in toward (1,1)
on a contour map of
f(x,y)=2≈+¥
0.95
1.05
1.05
0.8
1.2
1.2
0.5
1.5
1.5
f 共x, y兲 苷 2x
2
y
2
共1, 1兲
FIGURE 2 The elliptic paraboloid z=2≈+¥ appears to coincide with its tangent plane as we zoom in toward (1,1,3).
(c)
2
1
0
2
1
0
40
20
0
_20
y
z
x
(b)
2
0
_2
2
0
_2
40
20
0
_20
y
z
x
(a)
40
20
0
_20
y
z
4
2
0
_2
_4
x
4
2
0
_2
_4
f 共x, y兲 苷 2x
2
y
2
共1, 1, 3兲
共1, 1, 3兲
z 苷 4x 2y 3
z 3 苷 4共x 1兲 2共y 1兲
共1, 1, 3兲
f
x
共1, 1兲 苷 4 f
y
共1, 1兲 苷 2
f
x
共x, y兲 苷 4x f
y
共x, y兲 苷 2y
f 共x, y兲 苷 2x
2
y
2
共1, 1, 3兲
z 苷 2x
2
y
2
V
SECTION 15.4 TANGENT PLANES AND LINEAR APPROXIMATIONS
||||
929
Visual 15.4 shows an animation of
Figures 2 and 3.
TEC

LINEAR APPROXIMATIONS
In Example 1 we found that an equation of the tangent plane to the graph of the function
at the point is . Therefore, in view of the
visual evidence in Figures 2 and 3, the linear function of two variables
is a good approximation to when is near . The function L is called the
linearization of f at and the approximation
is called the linear approximation or tangent plane approximation of f at .
For instance, at the point (1.1, 0.95) the linear approximation gives
which is quite close to the true value of . But if
we take a point farther away from , such as , we no longer get a good approxi-
mation. In fact, whereas .
In general, we know from (2) that an equation of the tangent plane to the graph of a
function f of two variables at the point is
The linear function whose graph is this tangent plane, namely
is called the linearization of f at and the approximation
is called the linear approximation or the tangent plane approximation of at
We have defined tangent planes for surfaces , where has continuous first
partial derivatives. What happens if and are not continuous? Figure 4 pictures such a
function; its equation is
You can verify (see Exercise 46) that its partial derivatives exist at the origin and, in fact,
and , but and are not continuous. The linear approximation
would be , but at all points on the line . So a function of two
variables can behave badly even though both of its partial derivatives exist. To rule out
such behavior, we formulate the idea of a differentiable function of two variables.
Recall that for a function of one variable, , if x changes from a to we
defined the increment of as
⌬y 苷 f 共a ⫹⌬x兲 ⫺ f 共a兲
y
a ⫹⌬x,y 苷 f 共x兲
y 苷 xf 共x, y兲 苷
1
2
f 共x, y兲⬇0
f
y
f
x
f
y
共0, 0兲 苷 0f
x
共0, 0兲 苷 0
f 共x, y兲 苷
再
0
xy
x
2
⫹ y
2
if
if
共x, y兲 苷 共0, 0兲
共x, y兲 苷 共0, 0兲
f
y
f
x
fz 苷 f 共x, y兲
共a, b兲.f
f 共x, y兲⬇f 共a, b兲 ⫹ f
x
共a, b兲共x ⫺ a兲 ⫹ f
y
共a, b兲共y ⫺ b兲
4
共a, b兲
L共x, y兲 苷 f 共a, b兲 ⫹ f
x
共a, b兲共x ⫺ a兲 ⫹ f
y
共a, b兲共y ⫺ b兲
3
z 苷 f 共a, b兲 ⫹ f
x
共a, b兲共x ⫺ a兲 ⫹ f
y
共a, b兲共y ⫺ b兲
共a, b, f 共a, b兲兲
f 共2, 3兲 苷 17L共2, 3兲 苷 11
共2, 3兲共1, 1兲
f 共1.1, 0.95兲 苷 2共1.1兲
2
⫹ 共0.95兲
2
苷 3.3225
f 共1.1, 0.95兲⬇4共1.1兲 ⫹ 2共0.95兲 ⫺ 3 苷 3.3
共1, 1兲
f 共x, y兲⬇4x ⫹ 2y ⫺ 3
共1, 1兲
共1, 1兲共x, y兲f 共x, y兲
L共x, y兲 苷 4x ⫹ 2y ⫺ 3
z 苷 4x ⫹ 2y ⫺ 3共1, 1, 3兲f 共x, y兲 苷 2x
2
⫹ y
2
930
||||
CHAPTER 15 PARTIAL DERIVATIVES
z
y
x
f(x,y)=
xy
≈+¥
if (x,y)≠(0,0),
f(0,0)=0
FIGURE 4

In Chapter 3 we showed that if is differentiable at a, then
Now consider a function of two variables, , and suppose x changes from a to
and y changes from b to . Then the corresponding increment of is
Thus the increment represents the change in the value of when changes from
to . By analogy with (5) we define the differentiability of a func-
tion of two variables as follows.
DEFINITION If , then is differentiable at if can be
expressed in the form
where and as .
Definition 7 says that a differentiable function is one for which the linear approxima-
tion (4) is a good approximation when is near . In other words, the tangent
plane approximates the graph of f well near the point of tangency.
It’s sometimes hard to use Definition 7 directly to check the differentiability of a func-
tion, but the next theorem provides a convenient sufficient condition for differentiability.
THEOREM If the partial derivatives and exist near and are continu-
ous at , then is differentiable at .
EXAMPLE 2 Show that is differentiable at (1, 0) and find its lineariza-
tion there. Then use it to approximate .
SOLUTION The partial derivatives are
Both and are continuous functions, so is differentiable by Theorem 8. The
linearization is
The corresponding linear approximation is
so
Compare this with the actual value of . M
f 共1.1, ⫺0.1兲 苷 1.1e
⫺0.11
⬇ 0.98542
f 共1.1, ⫺0.1兲⬇1.1 ⫺ 0.1 苷 1
xe
xy
⬇ x ⫹ y
苷 1 ⫹ 1共x ⫺ 1兲 ⫹ 1 ⴢ y 苷 x ⫹ y
L共x, y兲 苷 f 共1, 0兲 ⫹ f
x
共1, 0兲共x ⫺ 1兲 ⫹ f
y
共1, 0兲共y ⫺ 0兲
ff
y
f
x
f
y
共1, 0兲 苷 1 f
x
共1, 0兲 苷 1
f
y
共x, y兲 苷 x
2
e
xy
f
x
共x, y兲 苷 e
xy
⫹ xye
xy
f 共1.1, ⫺0.1兲
f 共x, y兲 苷 xe
xy
V
共a, b兲f共a, b兲
共a, b兲f
y
f
x
8
共a, b兲共x, y兲
共⌬x, ⌬y兲 l 共0, 0兲
2
l 0
1
⌬z 苷 f
x
共a, b兲 ⌬x ⫹ f
y
共a, b兲 ⌬y ⫹
1
⌬x ⫹
2
⌬y
⌬z共a, b兲fz 苷 f 共x, y兲
7
共a ⫹⌬x, b ⫹⌬y兲共a, b兲
共x, y兲f⌬z
⌬z 苷 f 共a ⫹⌬x, b ⫹⌬y兲 ⫺ f 共a, b兲
6
zb ⫹⌬ya ⫹⌬x
z 苷 f 共x, y兲
where l 0 as ⌬x l 0⌬y 苷 f ⬘共a兲 ⌬x ⫹⌬x
5
f
SECTION 15.4 TANGENT PLANES AND LINEAR APPROXIMATIONS
||||
931
N This is Equation 3.5.5.
N Theorem 8 is proved in Appendix F.
FIGURE 5
1
0
_1
6
4
2
0
y
x
z
1
0
N Figure 5 shows the graphs of the function
and its linearization in Example 2.L
f
