Stewart J. Calculus

Подождите немного. Документ загружается.

THEOREM Suppose is a differentiable function of two or three variables. The

maximum value of the directional derivative is and it occurs when

has the same direction as the gradient vector .

PROOF From Equation 9 or 14 we have

where is the angle between and . The maximum value of is 1 and this

occurs when . Therefore the maximum value of is and it occurs when

, that is, when has the same direction as . M

EXAMPLE 6

(a) If , ﬁnd the rate of change of at the point in the direction from

to .

(b) In what direction does have the maximum rate of change? What is this maximum

rate of change?

SOLUTION

(a) We ﬁrst compute the gradient vector:

The unit vector in the direction of is , so the rate of change

of in the direction from to is

(b) According to Theorem 15, increases fastest in the direction of the gradient vector

. The maximum rate of change is

EXAMPLE 7 Suppose that the temperature at a point in space is given by

, where is measured in degrees Celsius and

, , in meters. In which direction does the temperature increase fastest at the point

? What is the maximum rate of increase?

SOLUTION The gradient of is

苷

160

共1 ⫹ x

⫹ 2y

⫹ 3z

兲

共⫺x i ⫺ 2y j ⫺ 3z k兲

苷 ⫺

160x

共1 ⫹ x

⫹ 2y

⫹ 3z

兲

i ⫺

320y

共1 ⫹ x

⫹ 2y

⫹ 3z

兲

j ⫺

480z

共1 ⫹ x

⫹ 2y

⫹ 3z

兲

ⵜT 苷

⭸T

⭸x

i ⫹

⭸T

⭸y

j ⫹

⭸T

⭸z

共1, 1, ⫺2兲

zyx

TT共x, y, z兲苷 80兾共1 ⫹ x

⫹ 2y

⫹ 3z

兲

共x, y, z兲

ⱍ

ⵜf 共2, 0兲

ⱍ

苷

ⱍ

具1, 2典

ⱍ

苷

ⵜf 共2, 0兲苷具1, 2典

苷 1

(

⫺

)

⫹ 2

(

)

苷 1

f 共2, 0兲苷 ⵜf 共2, 0兲 ⴢ u 苷具1, 2典 ⴢ

具

⫺

典

QPf

u 苷

具

⫺

典

苷具⫺1.5, 2典

ⵜf 共2, 0兲苷具1, 2典

ⵜf 共x, y兲苷具 f

, f

典苷具e

, xe

典

(

, 2

)

P共2, 0兲ff 共x, y兲苷 xe

ⵜfu

␪

苷 0

ⱍ

ⵜf

ⱍ

␪

苷 0

cos

␪

uⵜf

␪

f 苷 ⵜ f ⴢ u 苷

ⱍ

ⵜf

ⱍⱍ

ⱍ

cos

␪

苷

ⱍ

ⵜf

ⱍ

cos

␪

ⵜf 共x兲u

ⱍ

ⵜf 共x兲

ⱍ

f 共x兲

952

||||

CHAPTER 15 PARTIAL DERIVATIVES

Visual 15.6B provides visual

conﬁrmation of Theorem 15.

TEC

FIGURE 7

±f(2,0)

N At the function in Example 6 increases

fastest in the direction of the gradient vector

. Notice from Figure 7 that

this vector appears to be perpendicular to the

level curve through . Figure 8 shows the

graph of and the gradient vector.f

共2, 0兲

ⵜ f 共2, 0兲苷具1, 2典

共2, 0兲

FIGURE 8

At the point the gradient vector is

By Theorem 15 the temperature increases fastest in the direction of the gradient vector

or, equivalently, in the direction of or

the unit vector . The maximum rate of increase is the length of the

gradient vector:

Therefore the maximum rate of increase of temperature is . M

TANGENT PLANES TO LEVEL SURFACES

Suppose is a surface with equation , that is, it is a level surface of a func-

tion of three variables, and let be a point on . Let be any curve that lies

on the surface and passes through the point . Recall from Section 14.1 that the curve

is described by a continuous vector function . Let be the param-

eter value corresponding to ; that is, . Since lies on , any point

must satisfy the equation of , that is,

If , , and are differentiable functions of and is also differentiable, then we can use

the Chain Rule to differentiate both sides of Equation 16 as follows:

But, since and , Equation 17 can be written in

terms of a dot product as

In particular, when we have , so

Equation 18 says that the gradient vector at , , is perpendicular to the

tangent vector to any curve on that passes through . (See Figure 9.) If

, it is therefore natural to deﬁne the tangent plane to the level surface

at as the plane that passes through and has normal vector

. Using the standard equation of a plane (Equation 13.5.7), we can write the

equation of this tangent plane as

共x

, y

, z

兲共x ⫺ x

兲 ⫹ F

共x

, y

, z

兲共y ⫺ y

兲 ⫹ F

共x

, y

, z

兲共z ⫺ z

兲苷 0

ⵜF共x

, y

, z

兲

PP共x

, y

, z

兲F共x, y, z兲苷 k

ⵜF共x

, y

, z

兲苷 0

PSCr⬘共t

兲

ⵜF共x

, y

, z

兲P

ⵜF共x

, y

, z

兲 ⴢ r⬘共t

兲苷 0

r共t

兲苷具x

, y

, z

典t 苷 t

ⵜF ⴢ r⬘共t兲苷 0

r⬘共t兲苷具x⬘共t兲, y⬘共t兲, z⬘共t兲典ⵜF 苷具F

, F

典

⭸F

⭸x

⫹

⭸F

⭸y

⫹

⭸F

⭸z

苷 0

Ftzyx

(

x共t兲, y共t兲, z共t兲

)

苷 k

(

x共t兲, y共t兲, z共t兲

)

SCr共t

兲苷具x

, y

, z

典P

r共t兲苷具x共t兲, y共t兲, z共t兲典

CPS

CSP共x

, y

, z

兲F

F共x, y, z兲苷 kS

⬇ 4⬚C兾m

ⱍ

ⵜT共1, 1, ⫺2兲

ⱍ

苷

ⱍ

⫺i ⫺ 2 j ⫹ 6 k

ⱍ

苷

共⫺i ⫺ 2 j ⫹ 6 k兲兾

⫺i ⫺ 2 j ⫹ 6 kⵜT共1, 1, ⫺2兲苷

共⫺i ⫺ 2 j ⫹ 6 k兲

ⵜT共1, 1, ⫺2兲苷

160

256

共⫺i ⫺ 2 j ⫹ 6 k兲苷

共⫺i ⫺ 2 j ⫹ 6 k兲

共1, 1, ⫺2兲

SECTION 15.6 DIRECTIONAL DERIVATIVES AND THE GRADIENT VECTOR

||||

953

(

)

tangent plane

URE

The normal line to at is the line passing through and perpendicular to the tan-

gent plane. The direction of the normal line is therefore given by the gradient vector

and so, by Equation 13.5.3, its symmetric equations are

In the special case in which the equation of a surface is of the form (that

is, is the graph of a function of two variables), we can rewrite the equation as

and regard as a level surface (with ) of . Then

so Equation 19 becomes

which is equivalent to Equation 15.4.2. Thus our new, more general, deﬁnition of a tangent

plane is consistent with the deﬁnition that was given for the special case of Section 15.4.

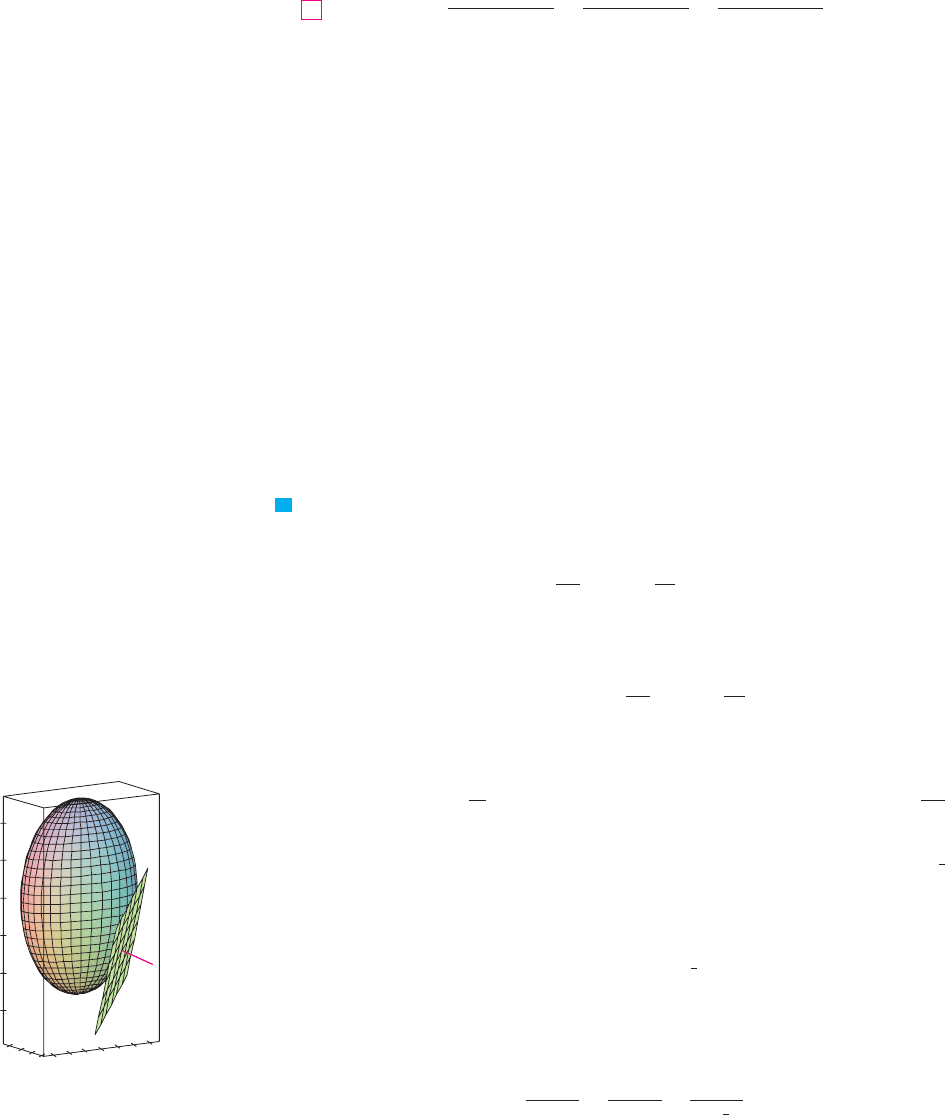
EXAMPLE 8 Find the equations of the tangent plane and normal line at the point

to the ellipsoid

SOLUTION The ellipsoid is the level surface (with ) of the function

Therefore we have

Then Equation 19 gives the equation of the tangent plane at as

which simpliﬁes to .

By Equation 20, symmetric equations of the normal line are

x ⫹ 2

⫺1

苷

y ⫺ 1

苷

z ⫹ 3

⫺

3x ⫺ 6y ⫹ 2z ⫹ 18 苷 0

⫺1共x ⫹ 2兲 ⫹ 2共y ⫺ 1兲 ⫺

共z ⫹ 3兲苷 0

共⫺2, 1, ⫺3兲

共⫺2, 1, ⫺3兲苷 ⫺

共⫺2, 1, ⫺3兲苷 2 F

共⫺2, 1, ⫺3兲苷 ⫺1

共x, y, z兲苷

共x, y, z兲苷 2y F

共x, y, z兲苷

F共x, y, z兲苷

⫹ y

⫹

k 苷 3

⫹ y

⫹

苷 3

共⫺2, 1, ⫺3兲

共x

, y

兲共x ⫺ x

兲 ⫹ f

共x

, y

兲共y ⫺ y

兲 ⫺ 共z ⫺ z

兲苷 0

共x

, y

, z

兲苷 ⫺1

共x

, y

, z

兲苷 f

共x

, y

兲

共x

, y

, z

兲苷 f

共x

, y

兲

Fk 苷 0S

F共x, y, z兲苷 f 共x, y兲 ⫺ z 苷 0

z 苷 f 共x, y兲S

x ⫺ x

共x

, y

, z

兲

苷

y ⫺ y

共x

, y

, z

兲

苷

z ⫺ z

共x

, y

, z

兲

ⵜF共x

, y

, z

兲

PPS

954

||||

CHAPTER 15 PARTIAL DERIVATIVES

N Figure 10 shows the ellipsoid, tangent plane,

and normal line in Example 8.

FIGURE 10

⫺2

⫺4

⫺6

⫺2

SIGNIFICANCE OF THE GRADIENT VECTOR

We now summarize the ways in which the gradient vector is signiﬁcant. We ﬁrst consider

a function of three variables and a point in its domain. On the one hand, we

know from Theorem 15 that the gradient vector gives the direction of fastest

increase of . On the other hand, we know that is orthogonal to the level sur-

face of through . (Refer to Figure 9.) These two properties are quite compatible intu-

itively because as we move away from on the level surface , the value of does not

change at all. So it seems reasonable that if we move in the perpendicular direction, we get

the maximum increase.

In like manner we consider a function of two variables and a point in its

domain. Again the gradient vector gives the direction of fastest increase of .

Also, by considerations similar to our discussion of tangent planes, it can be shown that

is perpendicular to the level curve that passes through . Again this

is intuitively plausible because the values of remain constant as we move along the

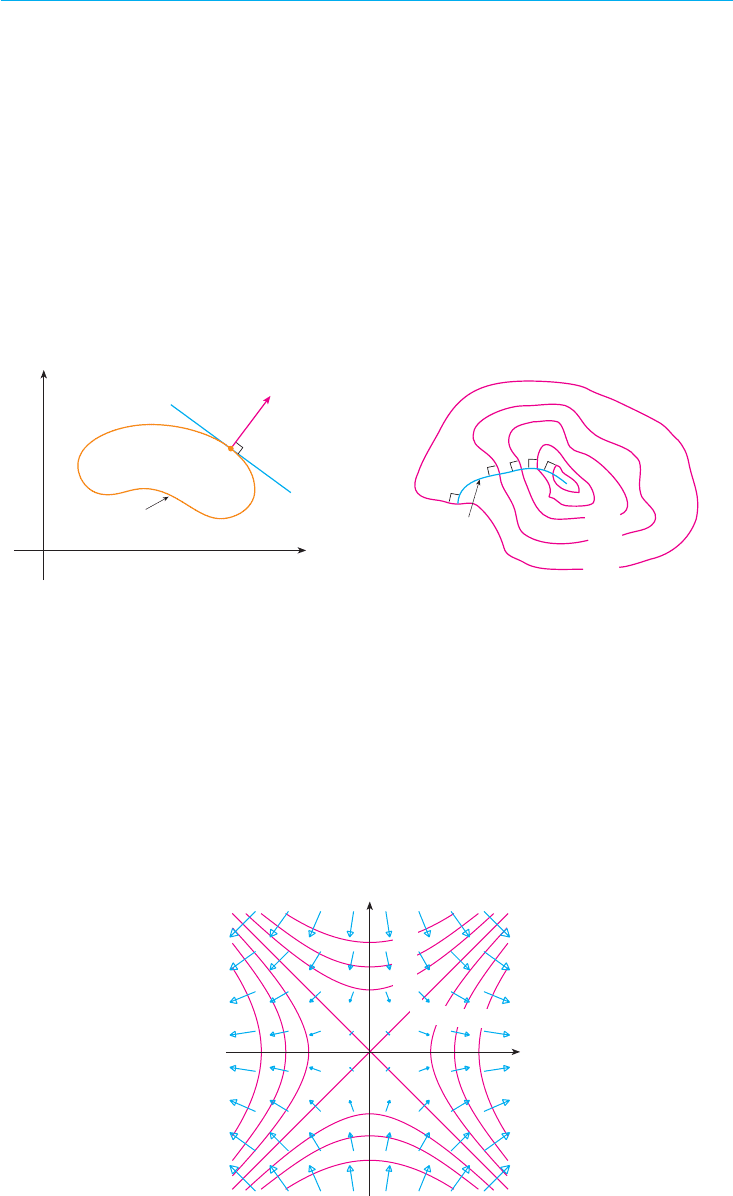
curve. (See Figure 11.)

If we consider a topographical map of a hill and let represent the height above

sea level at a point with coordinates , then a curve of steepest ascent can be drawn as

in Figure 12 by making it perpendicular to all of the contour lines. This phenomenon can

also be noticed in Figure 12 in Section 15.1, where Lonesome Creek follows a curve of

steepest descent.

Computer algebra systems have commands that plot sample gradient vectors. Each gra-

dient vector is plotted starting at the point . Figure 13 shows such a plot

(called a gradient vector ﬁeld ) for the function superimposed on a con-

tour map of f. As expected, the gradient vectors point “uphill” and are perpendicular to the

level curves.

FIGURE 13

f 共x, y兲苷 x

⫺ y

共a, b兲ⵜf 共a, b兲

共x, y兲

f 共x, y兲

P(x¸,y¸)

level curve

f(x,y)=k

±f(x¸,y¸)

300

200

100

curve of

steepest

ascent

FIGURE 11 FIGURE 12

Pf 共x, y兲苷 kⵜf 共x

, y

兲

fⵜf 共x

, y

兲

P共x

, y

兲f

fSP

PfS

ⵜf 共x

, y

, z

兲f

ⵜf 共x

, y

, z

兲

P共x

, y

, z

兲f

SECTION 15.6 DIRECTIONAL DERIVATIVES AND THE GRADIENT VECTOR

||||

955

956

||||

CHAPTER 15 PARTIAL DERIVATIVES

7–10

(a) Find the gradient of .

(b) Evaluate the gradient at the point .

vector .

7. ,,

8. ,,

9. ,,

10. ,,

11–17 Find the directional derivative of the function at the given

point in the direction of the vector .

12. ,,

13. ,,

14. ,,

15. ,,

16. ,,

17. ,,

18. Use the ﬁgure to estimate .

Find the directional derivative of at in

the direction of .

20. Find the directional derivative of at

in the direction of .

21– 26 Find the maximum rate of change of at the given point

and the direction in which it occurs.

21. ,

22. ,

24. ,

25. ,

26. ,

共⫺5, 1, 1兲f 共x, y, z兲苷 tan共x ⫹ 2y ⫹ 3z兲

共3, 6, ⫺2兲f 共x, y, z兲苷

⫹ y

⫹ z

共1, 1, ⫺1兲f 共x, y, z兲苷共x ⫹ y兲兾z

共1, 0兲f 共x, y兲苷 sin共xy兲

23.

共0, 0兲f 共p, q兲苷 qe

⫺p

⫹ pe

⫺q

共2, 4兲f 共x, y兲苷 y

兾x

Q共2, 4, 5兲P共1, ⫺1, 3兲

f 共x, y, z兲苷 xy ⫹ yz ⫹ zx

Q共5, 4兲

P共2, 8兲

f 共x, y兲苷

19.

(2,2)

±f(2,2)

f 共2, 2兲

v 苷 2 j ⫺ k共1, 1, 2兲t共x, y, z兲苷共x ⫹ 2y ⫹ 3z兲

3兾2

v 苷具⫺1, ⫺2, 2典共3, 2, 6兲f 共x, y, z兲苷

xyz

v 苷具5, 1, ⫺2典共0, 0, 0兲f 共x, y, z兲苷 xe

⫹ ye

⫹ ze

v 苷 5i ⫹ 10 j共1, 2兲t共r, s兲苷 tan

⫺1

共rs兲

v 苷 i ⫹ 3j共2, 1兲t共p, q兲苷 p

⫺ p

v 苷具⫺1, 2典共2, 1兲f 共x, y兲苷 ln共x

⫹ y

兲

v 苷具4, ⫺3典共3, 4兲f 共x, y兲苷 1 ⫹ 2x

11.

u 苷

具

典

P共1, 3, 1兲f 共x, y, z兲苷

x ⫹ yz

u 苷

具

, ⫺

典

P共3, 0, 2兲f 共x, y, z兲苷 xe

2 yz

u 苷

(

2i ⫹

)

P共1, 2兲f 共x, y兲苷 y

兾x

u 苷

(

i ⫺ j

)

P共⫺6, 4兲f 共x, y兲苷 sin共2x ⫹ 3y兲

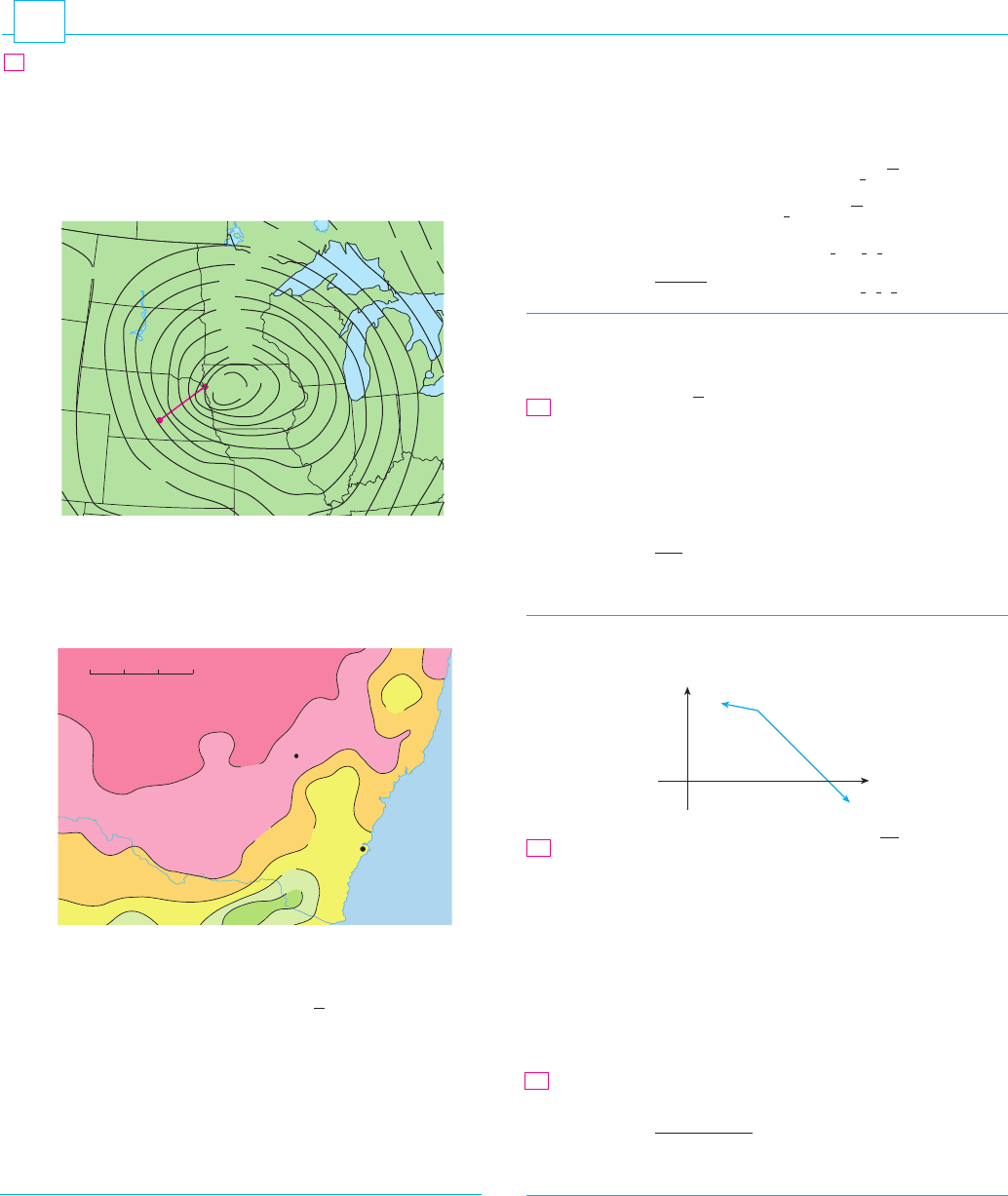
Level curves for barometric pressure (in millibars) are shown

for 6:00

AM on November 10, 1998. A deep low with pressure

972 mb is moving over northeast Iowa. The distance along the

red line from K (Kearney, Nebraska) to S (Sioux City, Iowa) is

300 km. Estimate the value of the directional derivative of the

pressure function at Kearney in the direction of Sioux City.

What are the units of the directional derivative?

2. The contour map shows the average maximum temperature for

November 2004 (in ). Estimate the value of the directional

derivative of this temperature function at Dubbo, New South

Wales, in the direction of Sydney. What are the units?

3. A table of values for the wind-chill index is given

in Exercise 3 on page 924. Use the table to estimate the value

of , where

4–6 Find the directional derivative of at the given point in the

direction indicated by the angle .

4. ,,

5. ,,

6. ,,

␪

苷

␲

兾3共2, 0兲f 共x, y兲苷 x sin共xy兲

␪

苷 2

␲

兾3共0, 4兲f 共x, y兲苷 ye

⫺x

␪

苷

␲

兾4共2, 1兲f 共x, y兲苷 x

⫺ y

␪

u 苷共i ⫹ j兲兾

f 共⫺20, 30兲

W 苷 f 共T,

v兲

Sydney

Dubbo

0 100 200 300

(Distance in kilometres)

⬚C

1012

1008

1004

1000

996

992

988

980

976

984

1016

1020

1024

972

From

Meteorology Today

, 8E by C. Donald Ahrens (2007 Thomson Brooks/Cole).

EXERCISES

15.6

SECTION 15.6 DIRECTIONAL DERIVATIVES AND THE GRADIENT VECTOR

||||

957

35.

Let be a function of two variables that has continuous

partial derivatives and consider the points , ,

, and . The directional derivative of at in the

direction of the vector is 3 and the directional derivative at

in the direction of is 26. Find the directional derivative of

at in the direction of the vector .

36.

For the given contour map draw the curves of steepest ascent

starting at and at .

37. Show that the operation of taking the gradient of a function has

the given property. Assume that and are differentiable func-

tions of and and that , are constants.

(a) (b)

38.

Sketch the gradient vector for the function whose

level curves are shown. Explain how you chose the direction

and length of this vector.

39– 44

Find equations of (a) the tangent plane and (b) the normal

line to the given surface at the speciﬁed point.

39.

40.

41.

42.

44. , 共0, 0, 1兲yz 苷 ln共x ⫹ z兲

共1, 0, 0兲z ⫹ 1 苷 xe

cos z

43.

共1 ⫹

␲

, 1, 1兲x ⫺ z 苷 4 arctan共yz兲

共2, 1, ⫺1兲x

⫺ 2y

⫹ z

⫹ yz 苷 2

共4, 7, 3兲y 苷 x

⫺ z

共3, 3, 5兲2共x ⫺ 2兲

⫹ 共y ⫺ 1兲

⫹ 共z ⫺ 3兲

苷 10

(4,6)

fⵜf 共4, 6兲

ⵜu

苷 nu

n⫺1

ⵜuⵜ

冉

冊

苷

ⵜu ⫺ u ⵜ

ⵜ共u

兲苷 u ⵜ

⫹

ⵜuⵜ共au ⫹ b

兲苷 a ⵜu ⫹ b ⵜ

bayx

AfD共6, 15兲C共1, 7兲

B共3, 3兲A共1, 3兲

(a) Show that a differentiable function decreases most

rapidly at in the direction opposite to the gradient vector,

that is, in the direction of .

(b) Use the result of part (a) to ﬁnd the direction in which the

function decreases fastest at the

point .

28.

Find the directions in which the directional derivative of

at the point has the value 1.

Find all points at which the direction of fastest change of the

function is .

30.

Near a buoy, the depth of a lake at the point with coordinates

is , where , , and are

measured in meters. A ﬁsherman in a small boat starts at the

point and moves toward the buoy, which is located at

. Is the water under the boat getting deeper or shallower

when he departs? Explain.

31.

The temperature in a metal ball is inversely proportional to

the distance from the center of the ball, which we take to be the

origin. The temperature at the point is .

(a) Find the rate of change of at in the direction

toward the point .

(b) Show that at any point in the ball the direction of greatest

increase in temperature is given by a vector that points

toward the origin.

32.

The temperature at a point is given by

where is measured in and , , in meters.

(a) Find the rate of change of temperature at the point

in the direction toward the point .

(b) In which direction does the temperature increase fastest

at ?

Suppose that over a certain region of space the electrical poten-

tial is given by .

(a) Find the rate of change of the potential at in the

direction of the vector .

(b) In which direction does change most rapidly at ?

34.

Suppose you are climbing a hill whose shape is given by the

equation , where , , and are

measured in meters, and you are standing at a point with coor-

dinates . The positive -axis points east and the

positive -axis points north.

(a) If you walk due south, will you start to ascend or descend?

At what rate?

(b) If you walk northwest, will you start to ascend or descend?

At what rate?

ascent in that direction? At what angle above the horizontal

does the path in that direction begin?

x共60, 40, 966兲

zyxz 苷 1000 ⫺ 0.005x

⫺ 0.01y

v 苷 i ⫹ j ⫺ k

P共3, 4, 5兲

V共x, y, z兲苷 5x

⫺ 3xy ⫹ xyzV

33.

共3, ⫺3, 3兲P共2, ⫺1, 2兲

zyx⬚CT

T共x, y, z兲苷 200e

⫺x

⫺3y

⫺9z

共x, y, z兲

共2, 1, 3兲

共1, 2, 2兲T

120⬚共1, 2, 2兲

共0, 0兲

共80, 60兲

zyxz 苷 200 ⫹ 0.02x

⫺ 0.001y

共x, y兲

i ⫹ jf 共x, y兲苷 x

⫹ y

⫺ 2x ⫺ 4y

29.

共0, 2兲f 共x, y兲苷 ye

⫺xy

共2, ⫺3兲

f 共x, y兲苷 x

y ⫺ x

⫺ⵜf 共x兲

27.

Openmirrors.com

56. Show that every normal line to the sphere

passes through the center of the sphere.

Show that the sum of the -, -, and -intercepts of any

tangent plane to the surface is a

constant.

58. Show that the pyramids cut off from the ﬁrst octant by any

tangent planes to the surface at points in the ﬁrst

octant must all have the same volume.

59. Find parametric equations for the tangent line to the curve of

intersection of the paraboloid and the ellipsoid

at the point .

60. (a) The plane intersects the cylinder

in an ellipse. Find parametric equations for the tangent

line to this ellipse at the point .

;

(b) Graph the cylinder, the plane, and the tangent line on the

same screen.

61. (a) Two surfaces are called orthogonal at a point of inter-

section if their normal lines are perpendicular at that

point. Show that surfaces with equations

and are orthogonal at a point where

and if and only if

(b) Use part (a) to show that the surfaces and

are orthogonal at every point of

intersection. Can you see why this is true without using

calculus?

62. (a) Show that the function is continuous and

the partial derivatives and exist at the origin but the

directional derivatives in all other directions do not exist.

;

(b) Graph near the origin and comment on how the graph

conﬁrms part (a).

Suppose that the directional derivatives of are known

at a given point in two nonparallel directions given by unit

vectors and . Is it possible to ﬁnd at this point? If so,

how would you do it?

64. Show that if is differentiable at

then

[Hint: Use Deﬁnition 15.4.7 directly.]

lim

x l x

f 共x兲 ⫺ f 共x

兲 ⫺ⵜf 共x

兲 ⴢ 共x ⫺ x

兲

ⱍ

x ⫺ x

ⱍ

苷 0

苷具x

, y

典,z 苷 f 共x, y兲

ⵜfvu

f 共x, y兲

63.

f 共x, y兲苷

⫹ y

⫹ z

苷 r

苷 x

⫹ y

⫹ F

苷 0

ⵜG 苷 0ⵜF 苷 0

PG共x, y, z兲苷 0

F共x, y, z兲苷 0

共1, 2, 1兲

⫹ y

苷 5y ⫹ z 苷 3

共⫺1, 1, 2兲4x

⫹ y

⫹ z

苷 9

z 苷 x

⫹ y

xyz 苷 1

⫹

苷

zyx

57.

⫹ y

⫹ z

苷 r

;

45– 46 Use a computer to graph the surface, the tangent plane,

and the normal line on the same screen. Choose the domain care-

fully so that you avoid extraneous vertical planes. Choose the

viewpoint so that you get a good view of all three objects.

45. ,

46. ,

47. If , ﬁnd the gradient vector and use it

to ﬁnd the tangent line to the level curve at the

point . Sketch the level curve, the tangent line, and the

gradient vector.

48. If , ﬁnd the gradient vector

and use it to ﬁnd the tangent line to the level curve

at the point . Sketch the level curve, the

tangent line, and the gradient vector.

49. Show that the equation of the tangent plane to the ellipsoid

at the point can be

written as

50. Find the equation of the tangent plane to the hyperboloid

at and express it in a

form similar to the one in Exercise 49.

51. Show that the equation of the tangent plane to the elliptic

paraboloid at the point can

be written as

52. At what point on the paraboloid is the tangent

plane parallel to the plane ?

53. Are there any points on the hyperboloid

where the tangent plane is parallel to the plane ?

54. Show that the ellipsoid and the sphere

are tangent to each

other at the point . (This means that they have a com-

mon tangent plane at the point.)

55. Show that every plane that is tangent to the cone

passes through the origin.x

⫹ y

苷 z

共1, 1, 2兲

⫹ y

⫹ z

⫺ 8x ⫺ 6y ⫺ 8z ⫹ 24 苷 0

⫹ 2y

⫹ z

苷 9

z 苷 x ⫹ y

⫺ y

⫺ z

苷 1

x ⫹ 2y ⫹ 3z 苷 1

y 苷 x

⫹ z

2xx

⫹

2yy

苷

z ⫹ z

共x

, y

, z

兲z兾c 苷 x

兾a

⫹ y

兾b

共x

, y

, z

兲x

兾a

⫹ y

兾b

⫺ z

兾c

苷 1

⫹

苷 1

共x

, y

, z

兲x

兾a

⫹ y

兾b

⫹ z

兾c

苷 1

共1, 2兲t共x, y兲苷 1

ⵜt共1, 2兲t共x, y兲苷 x

⫹ y

⫺ 4x

共3, 2兲

f 共x, y兲苷 6

ⵜf 共3, 2兲f 共x, y兲苷 xy

共1, 2, 3兲xyz 苷 6

共1, 1, 1兲xy ⫹ yz ⫹ zx 苷 3

958

||||

CHAPTER 15 PARTIAL DERIVATIVES

MAXIMUM AND MINIMUM VALUES

As we saw in Chapter 4, one of the main uses of ordinary derivatives is in ﬁnding maxi-

mum and minimum values. In this section we see how to use partial derivatives to locate

maxima and minima of functions of two variables. In particular, in Example 6 we will see

how to maximize the volume of a box without a lid if we have a ﬁxed amount of cardboard

to work with.

15.7

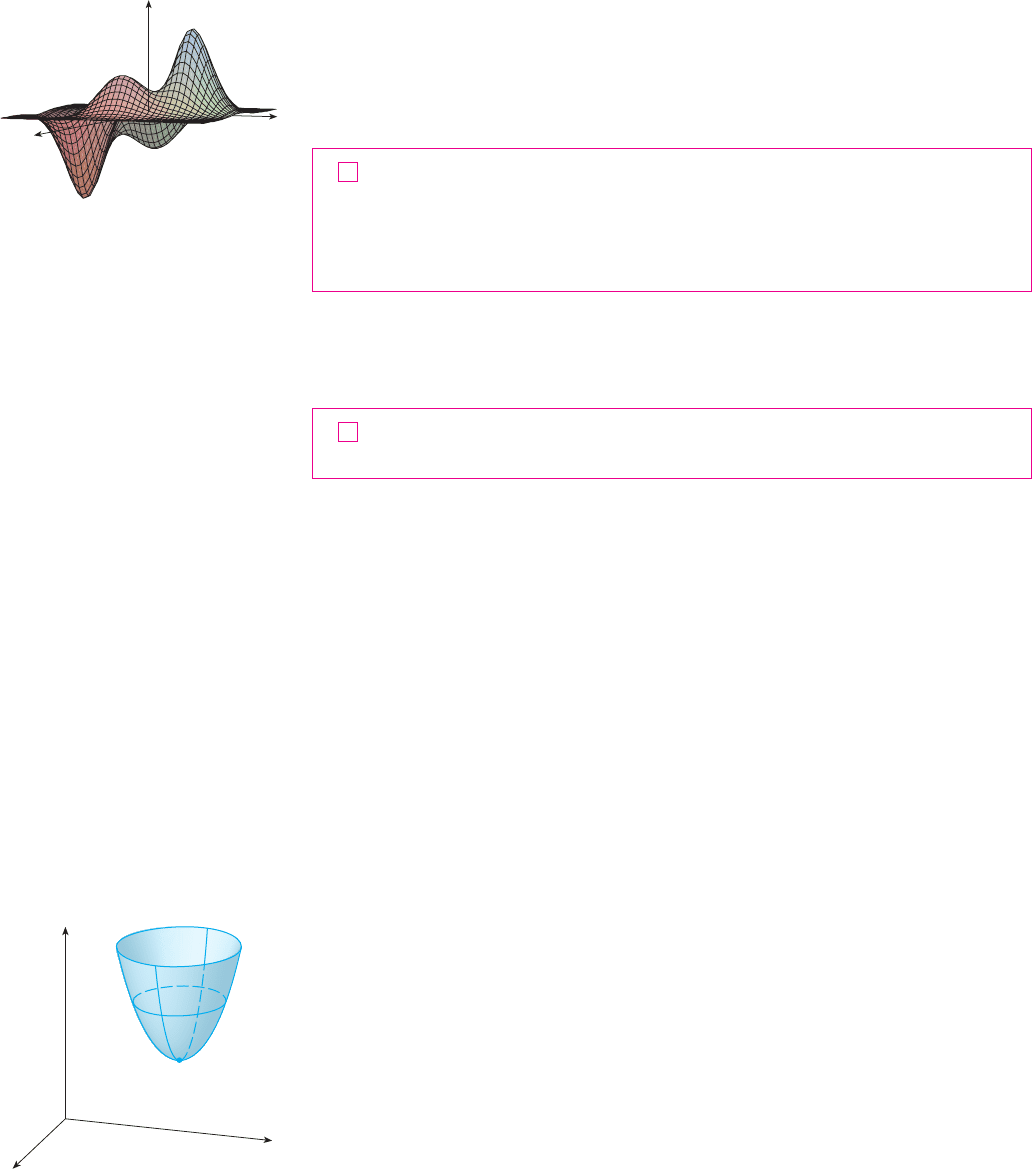
Look at the hills and valleys in the graph of shown in Figure 1. There are two points

where has a local maximum, that is, where is larger than nearby values of

. The larger of these two values is the absolute maximum. Likewise, has two local

minima, where is smaller than nearby values. The smaller of these two values is the

absolute minimum.

DEFINITION A function of two variables has a local maximum at if

when is near . [This means that for

all points in some disk with center .] The number is called a

local maximum value. If when is near , then has a

local minimum at and is a local minimum value.

If the inequalities in Deﬁnition 1 hold for all points in the domain of , then has

an absolute maximum (or absolute minimum) at .

THEOREM If has a local maximum or minimum at and the ﬁrst-order

partial derivatives of exist there, then and .

PROOF Let . If has a local maximum (or minimum) at , then has a

local maximum (or minimum) at , so by Fermat’s Theorem (see Theorem 4.1.4).

But (see Equation 15.3.1) and so . Similarly, by applying

Fermat’s Theorem to the function , we obtain . M

If we put and in the equation of a tangent plane (Equation

15.4.2), we get . Thus the geometric interpretation of Theorem 2 is that if the graph

of has a tangent plane at a local maximum or minimum, then the tangent plane must be

horizontal.

A point is called a critical point (or stationary point) of if and

, or if one of these partial derivatives does not exist. Theorem 2 says that if

has a local maximum or minimum at , then is a critical point of . However, as

in single-variable calculus, not all critical points give rise to maxima or minima. At a crit-

ical point, a function could have a local maximum or a local minimum or neither.

EXAMPLE 1 Let . Then

These partial derivatives are equal to 0 when and , so the only critical point

is . By completing the square, we ﬁnd that

Since and , we have for all values of and .

Therefore is a local minimum, and in fact it is the absolute minimum

of . This can be conﬁrmed geometrically from the graph of which is the elliptic

paraboloid with vertex shown in Figure 2.

共1, 3, 4兲

f,f

f 共1, 3兲苷 4

yxf 共x, y兲艌 4共y ⫺ 3兲

艌 0共x ⫺ 1兲

艌 0

f 共x, y兲苷 4 ⫹ 共x ⫺ 1兲

⫹ 共y ⫺ 3兲

共1, 3兲

y 苷 3x 苷 1

共x, y兲苷 2y ⫺ 6f

共x, y兲苷 2x ⫺ 2

f 共x, y兲苷 x

⫹ y

⫺ 2x ⫺ 6y ⫹ 14

f共a, b兲共a, b兲

共a, b兲苷 0

共a, b兲苷 0f共a, b兲

z 苷 z

共a, b兲苷 0f

共a, b兲苷 0

共a, b兲苷 0G共y兲苷 f 共a, y兲

共a, b兲苷 0t⬘共a兲苷 f

共a, b兲

t⬘共a兲苷 0a

t共a, b兲ft共x兲苷 f 共x, b兲

共a, b兲苷 0f

共a, b兲f

共a, b兲

ff共x, y兲

f 共a, b兲共a, b兲

f共a, b兲共x, y兲f 共x, y兲艌 f 共a, b兲

f 共a, b兲共a, b兲共x, y兲

f 共x, y兲艋 f 共a, b兲共a, b兲共x, y兲f 共x, y兲艋 f 共a, b兲

共a, b兲

f 共a, b兲

ff 共x, y兲

f 共a, b兲f共a, b兲

SECTION 15.7 MAXIMUM AND MINIMUM VALUES

||||

959

FIGURE 1

absolute

maximum

absolute

minimum

local

minimum

local

maximum

N Notice that the conclusion of Theorem 2 can

be stated in the notation of gradient vectors

as .ⵜf 共a, b兲苷 0

(1, 3, 4)

FIGURE 2

z=≈+¥-2x-6y+14

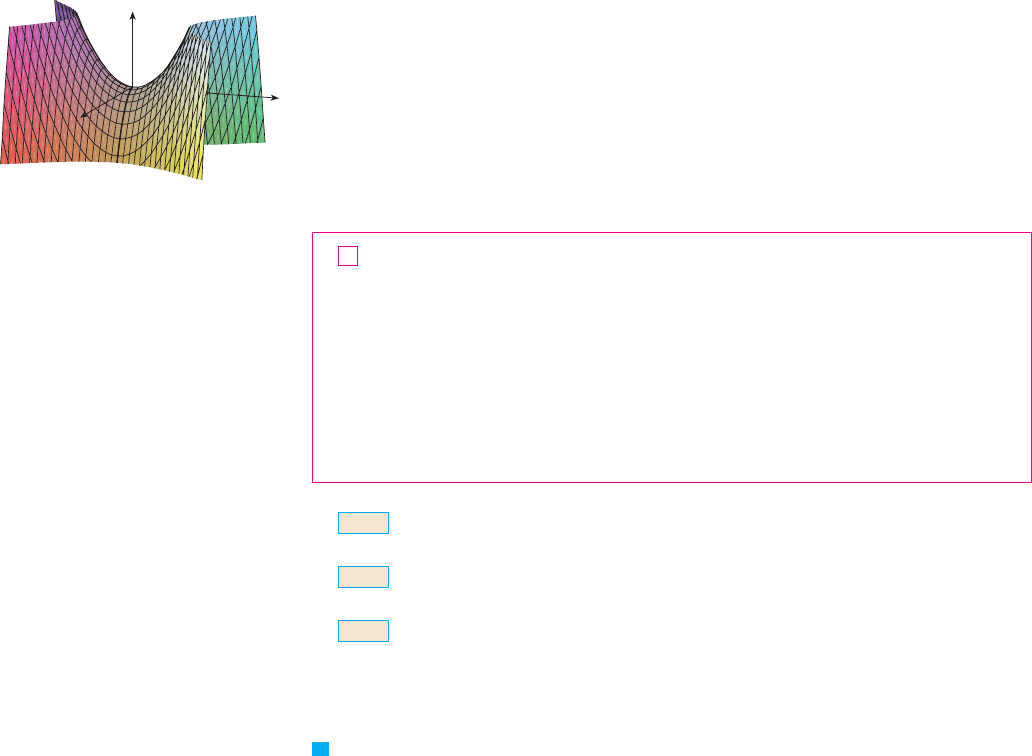
EXAMPLE 2 Find the extreme values of .

SOLUTION Since and , the only critical point is . Notice that

for points on the -axis we have , so (if ). However, for

points on the -axis we have , so (if ). Thus every disk

with center contains points where takes positive values as well as points where

takes negative values. Therefore can’t be an extreme value for , so has

no extreme value. M

Example 2 illustrates the fact that a function need not have a maximum or minimum

value at a critical point. Figure 3 shows how this is possible. The graph of is the hyper-

bolic paraboloid , which has a horizontal tangent plane ( ) at the origin.

You can see that is a maximum in the direction of the -axis but a minimum

in the direction of the -axis. Near the origin the graph has the shape of a saddle and so

is called a saddle point of .

We need to be able to determine whether or not a function has an extreme value at a

critical point. The following test, which is proved at the end of this section, is analogous

to the Second Derivative Test for functions of one variable.

SECOND DERIVATIVES TEST Suppose the second partial derivatives of are

continuous on a disk with center , and suppose that and

[that is, is a critical point of ]. Let

(a) If and , then is a local minimum.

(b) If and , then is a local maximum.

In case (c) the point is called a saddle point of and the graph of

crosses its tangent plane at .

If , the test gives no information: could have a local maximum or local

minimum at , or could be a saddle point of .

To remember the formula for , it’s helpful to write it as a determinant:

EXAMPLE 3 Find the local maximum and minimum values and saddle points of

SOLUTION We ﬁrst locate the critical points:

Setting these partial derivatives equal to 0, we obtain the equations

To solve these equations we substitute from the ﬁrst equation into the second

one. This gives

0 苷 x

⫺ x 苷 x共x

⫺ 1兲苷 x共x

⫺ 1兲共x

⫹ 1兲苷 x共x

⫺ 1兲共x

⫹ 1兲共x

⫹ 1兲

y 苷 x

⫺ x 苷 0andx

⫺ y 苷 0

苷 4y

⫺ 4xf

苷 4x

⫺ 4y

f 共x, y兲苷 x

⫹ y

⫺ 4xy ⫹ 1

D 苷

冟

苷 f

⫺ 共 f

兲

NOTE 3

f共a, b兲共a, b兲

fD 苷 0

NOTE 2

共a, b兲

ff共a, b兲

NOTE 1

f 共a, b兲D

⬍

f 共a, b兲f

共a, b兲

⬍

0D ⬎ 0

f 共a, b兲f

共a, b兲 ⬎ 0D ⬎ 0

D 苷 D共a, b兲苷 f

共a, b兲 f

共a, b兲 ⫺ 关 f

共a, b兲兴

f共a, b兲f

共a, b兲苷 0

共a, b兲苷 0共a, b兲

f共0, 0兲

xf 共0, 0兲苷 0

z 苷 0z 苷 y

⫺ x

fff 共0, 0兲苷 0f

f共0, 0兲

y 苷 0f 共x, y兲苷 y

⬎ 0x 苷 0y

x 苷 0f 共x, y兲苷 ⫺x

⬍

0y 苷 0x

共0, 0兲f

苷 2yf

苷 ⫺2x

f 共x, y兲苷 y

⫺ x

960

||||

CHAPTER 15 PARTIAL DERIVATIVES

FIGURE 3

z=¥-≈

so there are three real roots: , , . The three critical points are , ,

and .

Next we calculate the second partial derivatives and :

Since , it follows from case (c) of the Second Derivatives Test that

the origin is a saddle point; that is, has no local maximum or minimum at .

Since and , we see from case (a) of the test that

is a local minimum. Similarly, we have and

, so is also a local minimum.

The graph of is shown in Figure 4. M

EXAMPLE 4 Find and classify the critical points of the function

Also ﬁnd the highest point on the graph of .

SOLUTION The ﬁrst-order partial derivatives are

So to ﬁnd the critical points we need to solve the equations

From Equation 4 we see that either

In the ﬁrst case ( ), Equation 5 becomes , so and we

have the critical point .共0, 0兲

y 苷 0⫺4y共1 ⫹ y

兲苷 0x 苷 0

10y ⫺ 5 ⫺ 2x

苷 0orx 苷 0

5 x

⫺ 4y ⫺ 4y

苷 0

2 x共10y ⫺ 5 ⫺ 2x

兲苷 0

苷 10x

⫺ 8y ⫺ 8y

苷 20xy ⫺ 10x ⫺ 4x

f 共x, y兲苷 10x

y ⫺ 5x

⫺ 4y

⫺ x

⫺ 2y

FIGURE 5

0.9

0.5

_0.5

1.1

1.5

f 共⫺1, ⫺1兲苷 ⫺1f

共⫺1, ⫺1兲苷 12 ⬎ 0

D共⫺1, ⫺1兲苷 128 ⬎ 0f 共1, 1兲苷 ⫺1

共1, 1兲苷 12 ⬎ 0D共1, 1兲苷 128 ⬎ 0

共0, 0兲f

D共0, 0兲苷 ⫺16

⬍

D共x, y兲苷 f

⫺ 共 f

兲

苷 144x

⫺ 16

苷 12y

苷 ⫺4f

苷 12x

D共x, y兲

共⫺1, ⫺1兲

共1, 1兲共0, 0兲⫺11x 苷 0

SECTION 15.7 MAXIMUM AND MINIMUM VALUES

||||

961

FIGURE 4

z=x$+y$-4xy+1

N A contour map of the function in Example 3

is shown in Figure 5. The level curves near

and are oval in shape and indicate

that as we move away from or

in any direction the values of are increasing.

The level curves near , on the other hand,

resemble hyperbolas. They reveal that as we

move away from the origin (where the value of

is ), the values of decrease in some directions

but increase in other directions. Thus the contour

map suggests the presence of the minima and

saddle point that we found in Example 3.

共0, 0兲

共⫺1, ⫺1兲共1, 1兲

共⫺1, ⫺1兲

共1, 1兲

In Module 15.7 you can use contour

maps to estimate the locations of critical

points.

TEC