Stewart J. Calculus
Подождите немного. Документ загружается.


To derive this equation we assumed that defines implicitly as a function
of . The Implicit Function Theorem, proved in advanced calculus, gives conditions
under which this assumption is valid: It states that if is defined on a disk containing
where , , and and are continuous on the disk, then the
equation defines as a function of near the point and the derivative of
this function is given by Equation 6.
EXAMPLE 8 Find if .
SOLUTION The given equation can be written as
so Equation 6 gives
M
Now we suppose that is given implicitly as a function by an equation of
the form . This means that for all in the domain
of . If and are differentiable, then we can use the Chain Rule to differentiate the equa-
tion as follows:
But
so this equation becomes
If , we solve for and obtain the first formula in Equations 7. The formula
for is obtained in a similar manner.
Again, a version of the Implicit Function Theorem gives conditions under which
our assumption is valid: If is defined within a sphere containing , where
, , and , , and are continuous inside the sphere, then the
equation defines as a function of and near the point and this
function is differentiable, with partial derivatives given by (7).
共a, b, c兲yxzF共x, y, z兲 苷 0
F
z
F
y
F
x
F
z
共a, b, c兲 苷 0F共a, b, c兲 苷 0
共a, b, c兲F
z
y
苷
F
y
F
z
z
x
苷
F
x
F
z
7
z兾y
z兾xF兾z 苷 0
F
x
F
z
z
x
苷 0
x
共y兲 苷 0and
x
共x兲 苷 1
F
x
x
x
F
y
y
x
F
z
z
x
苷 0
F共x, y, z兲 苷 0
fFf
共x, y兲F共x, y, f 共x, y兲兲 苷 0F共x, y, z兲 苷 0
z 苷 f 共x, y兲z
dy
dx
苷
F
x
F
y
苷
3x
2
6y
3y
2
6x
苷
x
2
2y
y
2
2x
F共x, y兲 苷 x
3
y
3
6xy 苷 0
x
3
y
3
苷 6xyy
共a, b兲xyF共x, y兲 苷 0
F
y
F
x
F
y
共a, b兲 苷 0F共a, b兲 苷 0共a, b兲,
F
x
yF共x, y兲 苷 0
942
||||
CHAPTER 15 PARTIAL DERIVATIVES
N The solution to Example 8 should be
compared to the one in Example 2 in
Section 3.6.
EXAMPLE 9 Find and if .
SOLUTION Let . Then, from Equations 7, we have
M
z
y
苷
F
y
F
z
苷
3y
2
6xz
3z
2
6xy
苷
y
2
2xz
z
2
2xy
z
x
苷
F
x
F
z
苷
3x
2
6yz
3z
2
6xy
苷
x
2
2yz
z
2
2xy
F共x, y, z兲 苷 x
3
y
3
z
3
6xyz 1
x
3
y
3
z
3
6xyz 苷 1
z
y
z
x
SECTION 15.5 THE CHAIN RULE
||||
943
N The solution to Example 9 should be
compared to the one in Example 4 in
Section 15.3.
14. Let , where are
differentiable, and
Find and .
15. Suppose is a differentiable function of and , and
. Use the table of values
to calculate
16. Suppose is a differentiable function of and , and
Use the table of values in
Exercise 15 to calculate and
17–20 Use a tree diagram to write out the Chain Rule for the given
case. Assume all functions are differentiable.
, where ,
18. , where , ,
,
19. , where , ,
20. , where , ,
w 苷 w共p, q, r, s兲
v 苷 v共p, q, r, s兲u 苷 u共p, q, r, s兲t 苷 f 共u, v, w兲
t 苷 t共x, y兲s 苷 s共x, y兲r 苷 r共x, y兲
w 苷 f 共r, s, t兲
t 苷 t共u,
v, w兲z 苷 z共u, v, w兲
y 苷 y共u,
v, w兲x 苷 x共u, v, w兲R 苷 f 共x, y, z, t兲
y 苷 y共r, s, t兲x 苷 x共r, s, t兲u 苷 f 共x, y兲
17.
t
s
共1, 2兲.t
r
共1, 2兲
t共r, s兲 苷 f 共2r s, s
2
4r兲.
yxf
t
u
共0, 0兲 and t
v
共0, 0兲.
t共u,
v兲 苷 f 共e
u
sin v, e
u
cos v兲
yxf
W
t
共1, 0兲W
s
共1, 0兲
F
v
共2, 3兲 苷 10F
u
共2, 3兲 苷 1
v
t
共1, 0兲 苷 4u
t
共1, 0兲 苷 6
v
s
共1, 0兲 苷 5u
s
共1, 0兲 苷 2
v共1, 0兲 苷 3u共1, 0兲 苷 2
F, u, and
vW共s, t兲 苷 F共u共s, t兲, v共s, t兲兲
1–6 Use the Chain Rule to find or .
1. ,,
2. ,,
3. ,,
4. ,,
,, ,
6. ,, ,
7–12 Use the Chain Rule to find and .
7. ,,
8. ,,
9. ,,
10. ,,
,,
12. ,,
13. If , where is differentiable, and
find when .t 苷 3dz兾dt
f
y
共2, 7兲 苷 8f
x
共2, 7兲 苷 6
h共3兲 苷 4t共3兲 苷 5
h共3兲 苷 7t共3兲 苷 2
y 苷 h共t兲x 苷 t共t兲
fz 苷 f 共x, y兲
v 苷 3s 2tu 苷 2s 3tz 苷 tan共u兾v兲
苷
s
s
2
t
2
r 苷 stz 苷 e
r
cos
11.
y 苷 t兾sx 苷 s兾tz 苷 e
x2y
苷 s
2
t
苷 st
2
z 苷 sin
cos
y 苷 1 2stx 苷 s
2
t
2
z 苷 arcsin共x y兲
y 苷 s sin tx 苷 s cos tz 苷 x
2
y
3
z兾tz兾s
z 苷 tan ty 苷 cos tx 苷 sin t
w 苷 ln
s
x
2
y
2
z
2
z 苷 1 2ty 苷 1 tx 苷 t
2
w 苷 xe
y兾z
5.
y 苷 1 e
t
x 苷 e
t
z 苷 tan
1
共y兾x兲
y 苷 cos tx 苷 ln tz 苷
s
1 x
2
y
2
y 苷 1兾tx 苷 5t
4
z 苷 cos共x 4y兲
y 苷 e
t
x 苷 sin tz 苷 x
2
y
2
xy
d
w兾dtdz兾dt
EXERCISES
15.5
3648
6325共1, 2兲
共0, 0兲
f
y
f
x
tf
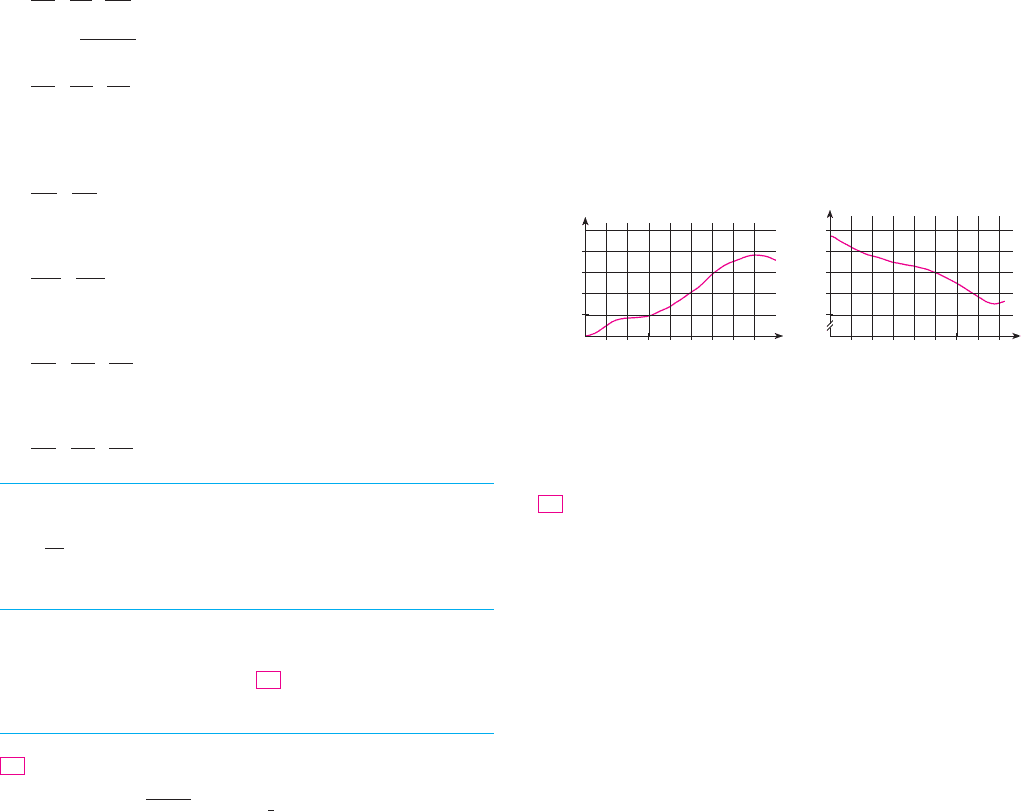
944
||||
CHAPTER 15 PARTIAL DERIVATIVES
37. The speed of sound traveling through ocean water with salinity
35 parts per thousand has been modeled by the equation
where is the speed of sound (in meters per second), is the
temperature (in degrees Celsius), and is the depth below the
ocean surface (in meters). A scuba diver began a leisurely dive
into the ocean water; the diver’s depth and the surrounding
water temperature over time are recorded in the following
graphs. Estimate the rate of change (with respect to time) of
the speed of sound through the ocean water experienced by the
diver 20 minutes into the dive. What are the units?
38. The radius of a right circular cone is increasing at a rate of
in兾s while its height is decreasing at a rate of in兾s. At
what rate is the volume of the cone changing when the radius is
120 in. and the height is 140 in.?
The length 艎, width , and height of a box change with
time. At a certain instant the dimensions are and
m, and 艎 and are increasing at a rate of 2 m兾s
while is decreasing at a rate of 3 m兾s. At that instant find the
rates at which the following quantities are changing.
(a) The volume
(b) The surface area
(c) The length of a diagonal
40. The voltage in a simple electrical circuit is slowly decreasing
as the battery wears out. The resistance is slowly increasing
as the resistor heats up. Use Ohm’s Law, , to find how
the current is changing at the moment when ,
A, V兾s, and .
41. The pressure of 1 mole of an ideal gas is increasing at a rate
of kPa兾s and the temperature is increasing at a rate of
K兾s. Use the equation in Example 2 to find the rate of
change of the volume when the pressure is 20 kPa and the
temperature is 320 K.
42. Car A is traveling north on Highway 16 and car B is traveling
west on Highway 83. Each car is approaching the intersection
of these highways. At a certain moment, car A is 0.3 km from
the intersection and traveling at 90 km兾h while car B is 0.4 km
from the intersection and traveling at 80 km兾h. How fast is the
distance between the cars changing at that moment?
43. One side of a triangle is increasing at a rate of and a
second side is decreasing at a rate of . If the area of the 2 cm兾s
3 cm兾s
0.15
0.05
dR兾dt 苷 0.03 兾sdV兾dt 苷 0.01I 苷 0.08
R 苷 400 I
V 苷 IR
R
V
h
ww 苷 h 苷 2
艎 苷 1 m
h
w
39.
2.51.8
t
(min)
T
10
12
10 20 30 40
14
16
8
t
(min)
D
5
10
10 20 30 40
15
20
D
TC
C 苷 1449.2 4.6T 0.055T
2
0.00029T
3
0.016D
21– 26 Use the Chain Rule to find the indicated partial derivatives.
21. ,,;
, , when , ,
22. ,,;
, , when , ,
23. ,
,,;
, when
24. ,, , ;
, when
25. ,,,;
, , when
26. ,,,;
, , when
27–30 Use Equation 6 to find .
27. 28.
29. 30.
31–34 Use Equations 7 to find and .
31.
33. 34.
The temperature at a point is , measured in degrees
Celsius. A bug crawls so that its position after seconds is
given by , where and are measured
in centimeters. The temperature function satisfies
and . How fast is the temperature rising on the
bug’s path after 3 seconds?
36. Wheat production in a given year depends on the average
temperature and the annual rainfall . Scientists estimate
that the average temperature is rising at a rate of 0.15°C兾year
and rainfall is decreasing at a rate of 0.1 cm兾year. They also
estimate that, at current production levels,
and .
(a) What is the significance of the signs of these partial
derivatives?
(b) Estimate the current rate of change of wheat production,
.dW兾dt
W兾R 苷 8
W兾T 苷 2
RT
W
T
y
共2, 3兲 苷 3
T
x
共2, 3兲 苷 4
yxx 苷
s
1 t
, y 苷 2
1
3
t
t
T共x, y兲共x, y兲
35.
yz 苷 ln共x z兲x z 苷 arctan共yz兲
xyz 苷 cos共x y z兲
32.
x
2
y
2
z
2
苷 3xyz
z兾yz兾x
sin x cos y 苷 sin x cos ycos共x y兲 苷 xe
y
y
5
x
2
y
3
苷 1 ye
x
2
s
xy
苷 1 x
2
y
dy兾dx
r 苷 1, s 苷 0, t 苷 1
Y
t
Y
s
Y
r
w 苷 t rv 苷 s tu 苷 r sY 苷 w tan
1
共uv兲
p 苷 2, r 苷 3,
苷 0
u
u
r
u
p
z 苷 p ry 苷 pr sin
x 苷 pr cos
u 苷 x
2
yz
u 苷 3, v 苷 1
M
v
M
u
z 苷 u
vy 苷 u vx 苷 2uvM 苷 xe
yz
2
x 苷 y 苷 1
R
y
R
x
w 苷 2xyv 苷 2x yu 苷 x 2y
R 苷 ln共u
2
v
2
w
2
兲
t 苷 0y 苷 2x 苷 1
u
t
u
y
u
x
s 苷 x y sin tr 苷 y x cos tu 苷
s
r
2
s
2
w 苷 0v 苷 1u 苷 2
z
w
z
v
z
u
y 苷 u
ve
w
x 苷 uv
2
w
3
z 苷 x
2
xy
3
SECTION 15.5 THE CHAIN RULE
||||
945
50. If , where and , show that
51. If , where and , find .
(Compare with Example 7.)
52. If , where and , find
(a) , (b) , and (c) .
53. If , where and , show that
54. Suppose , where and .
(a) Show that
(b) Find a similar formula for .
55. A function f is called homogeneous of degree n if it satisfies
the equation for all t, where n is a positive
integer and f has continuous second-order partial derivatives.
(a) Verify that is homogeneous
of degree 3.
(b) Show that if is homogeneous of degree , then
[Hint: Use the Chain Rule to differentiate with
respect to t.]
56. If is homogeneous of degree , show that
57. If is homogeneous of degree , show that
58. Suppose that the equation implicitly defines each
of the three variables , , and as functions of the other two:
, , . If is differentiable and
, , and are all nonzero, show that
z
x
x
y
y
z
苷 1
F
z
F
y
F
x
Fx 苷 h共y, z兲y 苷 t共x, z兲z 苷 f 共x, y兲
zyx
F共x, y, z兲 苷 0
f
x
共tx, ty兲 苷 t
n1
f
x
共x, y兲
nf
x
2
2
f
x
2
2xy
2
f
x y
y
2
2
f
y
2
苷 n共n 1兲f 共x, y兲
nf
f 共tx, ty兲
x
f
x
y
f
y
苷 nf共x, y兲
nf
f 共x, y兲 苷 x
2
y 2xy
2
5y
3
f 共tx, ty兲 苷 t
n
f 共x, y兲
2
z兾s t
z
x
2
x
t
2
z
y
2
y
t
2
2
z
t
2
苷
2
z
x
2
冉
x
t
冊
2
2
2
z
x y
x
t
y
t
2
z
y
2
冉
y
t
冊
2
y 苷 h共s, t兲x 苷 t共s, t兲z 苷 f 共x, y兲
2
z
x
2
2
z
y
2
苷
2
z
r
2
1
r
2
2
z
2
1
r
z
r
y 苷 r sin
x 苷 r cos
z 苷 f 共x, y兲
2
z兾r
z兾
z兾r
y 苷 r sin
x 苷 r cos
z 苷 f 共x, y兲
2
z兾r sy 苷 2rsx 苷 r
2
s
2
z 苷 f 共x, y兲
2
u
x
2
2
u
y
2
苷 e
2s
冋
2
u
s
2
2
u
t
2
册
y 苷 e
s
sin tx 苷 e
s
cos tu 苷 f 共x, y兲
triangle remains constant, at what rate does the angle between
the sides change when the first side is 20 cm long, the second
side is 30 cm, and the angle is ?
44. If a sound with frequency is produced by a source traveling
along a line with speed and an observer is traveling with
speed along the same line from the opposite direction toward
the source, then the frequency of the sound heard by the
observer is
where is the speed of sound, about . (This is the
Doppler effect.) Suppose that, at a particular moment, you
are in a train traveling at and accelerating at .
A train is approaching you from the opposite direction on the
other track at , accelerating at , and sounds its
whistle, which has a frequency of 460 Hz. At that instant, what
is the perceived frequency that you hear and how fast is it
changing?
45– 48 Assume that all the given functions are differentiable.
If , where and , (a) find
and and (b) show that
46. If , where and , show that
If , show that .
48. If , where and , show that
49–54 Assume that all the given functions have continuous
second-order partial derivatives.
49. Show that any function of the form
is a solution of the wave equation
[Hint: Let , .]
v 苷 x atu 苷 x at
2
z
t
2
苷 a
2
2
z
x
2
z 苷 f 共x at兲 t共x at兲
冉
z
x
冊
2
冉
z
y
冊
2
苷
z
s
z
t
y 苷 s tx 苷 s tz 苷 f 共x, y兲
z
x
z
y
苷 0z 苷 f 共x y兲
47.
冉
u
x
冊
2
冉
u
y
冊
2
苷 e
2s
冋冉
u
s
冊
2
冉
u
t
冊
2
册
y 苷 e
s
sin tx 苷 e
s
cos tu 苷 f 共x, y兲
冉
z
x
冊
2
冉
z
y
冊
2
苷
冉
z
r
冊
2
1
r
2
冉
z
冊
2
z兾
z兾ry 苷 r sin
x 苷 r cos
z 苷 f 共x, y兲
45.
1.4 m兾s
2
40 m兾s
1.2 m兾s
2
34 m兾s
332 m兾sc
f
o
苷
冉
c v
o
c v
s
冊
f
s
v
o
v
s
f
s
兾6
DIRECTIONAL DERIVATIVES AND THE GRADIENT VECTOR
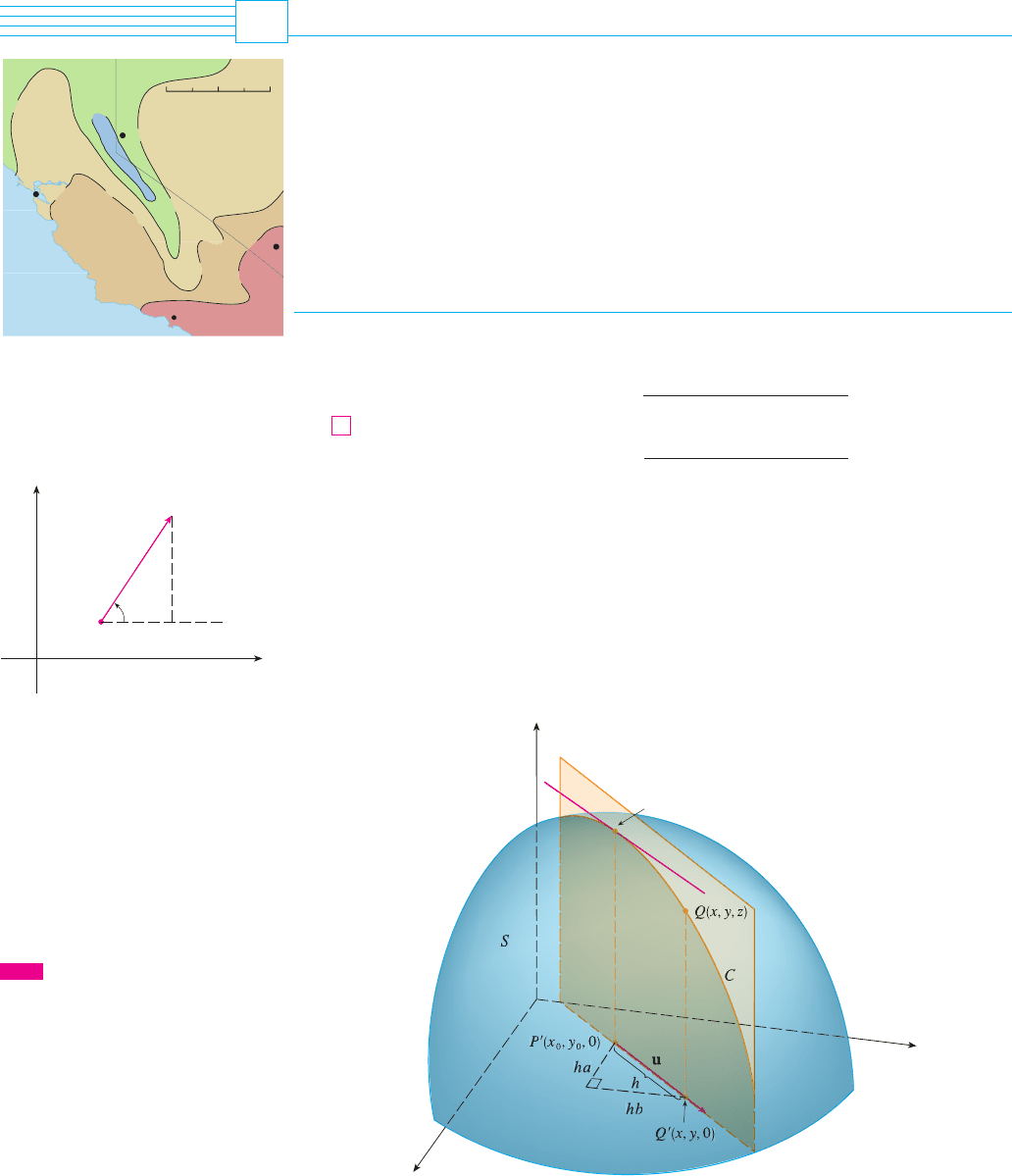
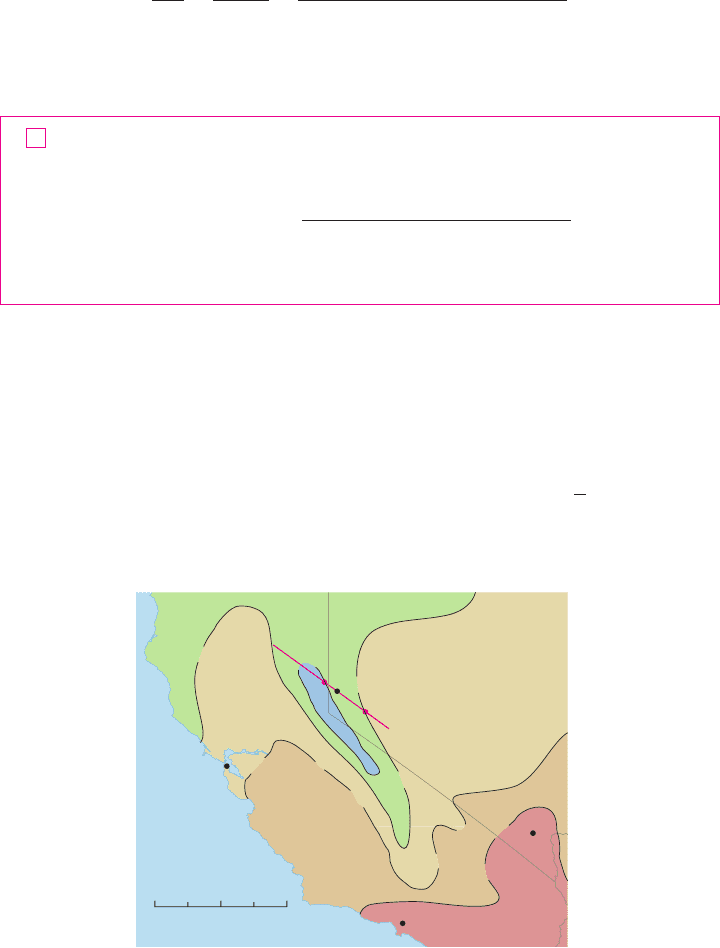
The weather map in Figure 1 shows a contour map of the temperature function for
the states of California and Nevada at 3:00
PM on a day in October. The level curves, or
isothermals, join locations with the same temperature. The partial derivative at a loca-
tion such as Reno is the rate of change of temperature with respect to distance if we travel
east from Reno; is the rate of change of temperature if we travel north. But what if we
want to know the rate of change of temperature when we travel southeast (toward Las
Vegas), or in some other direction? In this section we introduce a type of derivative, called
a directional derivative, that enables us to find the rate of change of a function of two or
more variables in any direction.
DIRECTIONAL DERIVATIVES
Recall that if , then the partial derivatives and are defined as
and represent the rates of change of in the - and -directions, that is, in the directions of
the unit vectors and .
Suppose that we now wish to find the rate of change of at in the direction of
an arbitrary unit vector . (See Figure 2.) To do this we consider the surface
with equation (the graph of ) and we let . Then the point
lies on . The vertical plane that passes through in the direction of inter-
sects in a curve . (See Figure 3.) The slope of the tangent line to at the point is
the rate of change of in the direction of .
FI
GU
RE
3
P
(x
¸
,
y
¸
,
z
¸
)
T
y
x
z
uz
PCTCS
uPSP共x
0
, y
0
, z
0
兲
z
0
苷 f 共x
0
, y
0
兲fz 苷 f 共x, y兲
Su 苷 具a, b 典
共x
0
, y
0
兲z
ji
yxz
f
y
共x
0
, y
0
兲 苷 lim
h
l
0
f 共x
0
, y
0
h兲 f 共x
0
, y
0
兲
h
f
x
共x
0
, y
0
兲 苷 lim
h
l
0
f 共x
0
h, y
0
兲 f 共x
0
, y
0
兲
h
1
f
y
f
x
z 苷 f 共x, y兲
T
y
T
x
T共x, y兲
15.6
946
||||
CHAPTER 15 PARTIAL DERIVATIVES
FIGURE 2
A unit vector u=ka,bl=kcos¨, sin¨l
y
0
x
(x¸,y¸)
cos¨
sin¨
¨
u
Visual 15.6A animates Figure 3 by
rotating and therefore .Tu
TEC
FIGURE 1
Los Angeles
Las Vegas
Reno
50
60
60
70
70
80
San Francisco
0
(Distance in miles)
50 100 150 200
© 1997 USA Today
If is another point on and , are the projections of , on the -plane,
then the vector P
B
Q is parallel to and so
P
B
Q
for some scalar . Therefore , , so , ,
and
If we take the limit as , we obtain the rate of change of (with respect to distance)
in the direction of , which is called the directional derivative of in the direction of .
DEFINITION The directional derivative of at in the direction of a
unit vector is
if this limit exists.
By comparing Definition 2 with Equations (1), we see that if , then
and if , then . In other words, the partial derivatives of
with respect to and are just special cases of the directional derivative.
EXAMPLE 1 Use the weather map in Figure 1 to estimate the value of the directional
derivative of the temperature function at Reno in the southeasterly direction.
SOLUTION The unit vector directed toward the southeast is , but we won’t
need to use this expression. We start by drawing a line through Reno toward the south-
east. (See Figure 4.)
We approximate the directional derivative by the average rate of change of the
temperature between the points where this line intersects the isothermals andT 苷 50
D
u
T
FIGURE 4
s
50
60
0
(Distance in miles)
50 100 150 200
Los Angeles
Las Vega
Reno
60
70
70
80
San Francisco
© 1997 USA Today
u 苷 共i j兲兾
s
2
yx
fD
j
f 苷 f
y
u 苷 j 苷 具0, 1典D
i
f 苷 f
x
u 苷 i 苷 具1, 0典
D
u
f 共x
0
, y
0
兲 苷 lim
h
l
0
f 共x
0
ha, y
0
hb兲 f 共x
0
, y
0
兲
h
u 苷 具a, b 典
共x
0
, y
0
兲f
2
ufu
zh l 0
z
h
苷
z z
0
h
苷
f 共x
0
ha, y
0
hb兲 f 共x
0
, y
0
兲
h
y 苷 y
0
hbx 苷 x
0
hay y
0
苷 hbx x
0
苷 hah
苷 hu 苷 具ha, hb典
u
xyQPQPCQ共x, y, z兲
SECTION 15.6 DIRECTIONAL DERIVATIVES AND THE GRADIENT VECTOR
||||
947
. The temperature at the point southeast of Reno is and the temperature
at the point northwest of Reno is . The distance between these points looks to
be about 75 miles. So the rate of change of the temperature in the southeasterly direction
is
M
When we compute the directional derivative of a function defined by a formula, we gen-
erally use the following theorem.
THEOREM If is a differentiable function of and , then has a directional
derivative in the direction of any unit vector and
PROOF If we define a function of the single variable by
then, by the definition of a derivative, we have
On the other hand, we can write , where , , so the
Chain Rule (Theorem 15.5.2) gives
If we now put , then , , and
Comparing Equations 4 and 5, we see that
M
If the unit vector makes an angle with the positive -axis (as in Figure 2), then we
can write and the formula in Theorem 3 becomes
EXAMPLE 2 Find the directional derivative if
and is the unit vector given by angle . What is ?D
u
f 共1, 2兲
苷
兾6u
f 共x, y兲 苷 x
3
3xy 4y
2
D
u
f 共x, y兲
D
u
f 共x, y兲 苷 f
x
共x, y兲 cos
f
y
共x, y兲 sin
6
u 苷 具cos
, sin
典
x
u
D
u
f 共x
0
, y
0
兲 苷 f
x
共x
0
, y
0
兲a f
y
共x
0
, y
0
兲b
t共0兲 苷 f
x
共x
0
, y
0
兲a f
y
共x
0
, y
0
兲b
5
y 苷 y
0
x 苷 x
0
h 苷 0
t共h兲 苷
f
x
dx
dh
f
y
dy
dh
苷 f
x
共x, y兲 a f
y
共x, y兲 b
y 苷 y
0
hbx 苷 x
0
hat共h兲 苷 f 共x, y兲
苷 D
u
f 共x
0
, y
0
兲
t共0兲 苷 lim
h
l
0
t共h兲 t共0兲
h
苷 lim
h
l
0
f 共x
0
ha, y
0
hb兲 f 共x
0
, y
0
兲
h
4
t共h兲 苷 f 共x
0
ha, y
0
hb兲
ht
D
u
f 共x, y兲 苷 f
x
共x, y兲 a f
y
共x, y兲 b
u 苷 具a, b 典
fyxf
3
D
u
T ⬇
60 50
75
苷
10
75
⬇ 0.13F兾mi
T 苷 50 F
T 苷 60 FT 苷 60
948
||||
CHAPTER 15 PARTIAL DERIVATIVES

SOLUTION Formula 6 gives
Therefore
M
THE GRADIENT VECTOR
Notice from Theorem 3 that the directional derivative can be written as the dot product of
two vectors:
The first vector in this dot product occurs not only in computing directional derivatives but
in many other contexts as well. So we give it a special name (the gradient of ) and a spe-
cial notation (grad or , which is read “del ”).
DEFINITION If is a function of two variables and , then the gradient of
is the vector function defined by
EXAMPLE 3 If , then
and M
With this notation for the gradient vector, we can rewrite the expression (7) for the
directional derivative as
This expresses the directional derivative in the direction of as the scalar projection of the
gradient vector onto .u
u
D
u
f 共x, y兲 苷 f 共x, y兲 ⴢ u
9
f 共0, 1兲 苷 具2, 0典
f 共x, y兲 苷 具 f
x
, f
y
典 苷 具cos x ye
xy
, xe
xy
典
f 共x, y兲 苷 sin x e
xy
f 共x, y兲 苷 具 f
x
共x, y兲, f
y
共x, y兲典 苷
f
x
i
f
y
j
f
fyxf
8
fff
f
苷 具 f
x
共x, y兲, f
y
共x, y兲典 ⴢ u
苷 具 f
x
共x, y兲, f
y
共x, y兲典 ⴢ 具a, b典
D
u
f 共x, y兲 苷 f
x
共x, y兲 a f
y
共x, y兲 b
7
D
u
f 共1, 2兲 苷
1
2
[
3
s
3
共1兲
2
3共1兲
(
8 3
s
3
)
共2兲
]
苷
13 3
s
3
2
苷
1
2
[
3
s
3
x
2
3x
(
8 3
s
3
)
y
]
苷 共3x
2
3y兲
s
3
2
共3x 8y兲
1
2
D
u
f 共x, y兲 苷 f
x
共x, y兲 cos
6
f
y
共x, y兲 sin
6
SECTION 15.6 DIRECTIONAL DERIVATIVES AND THE GRADIENT VECTOR
||||
949
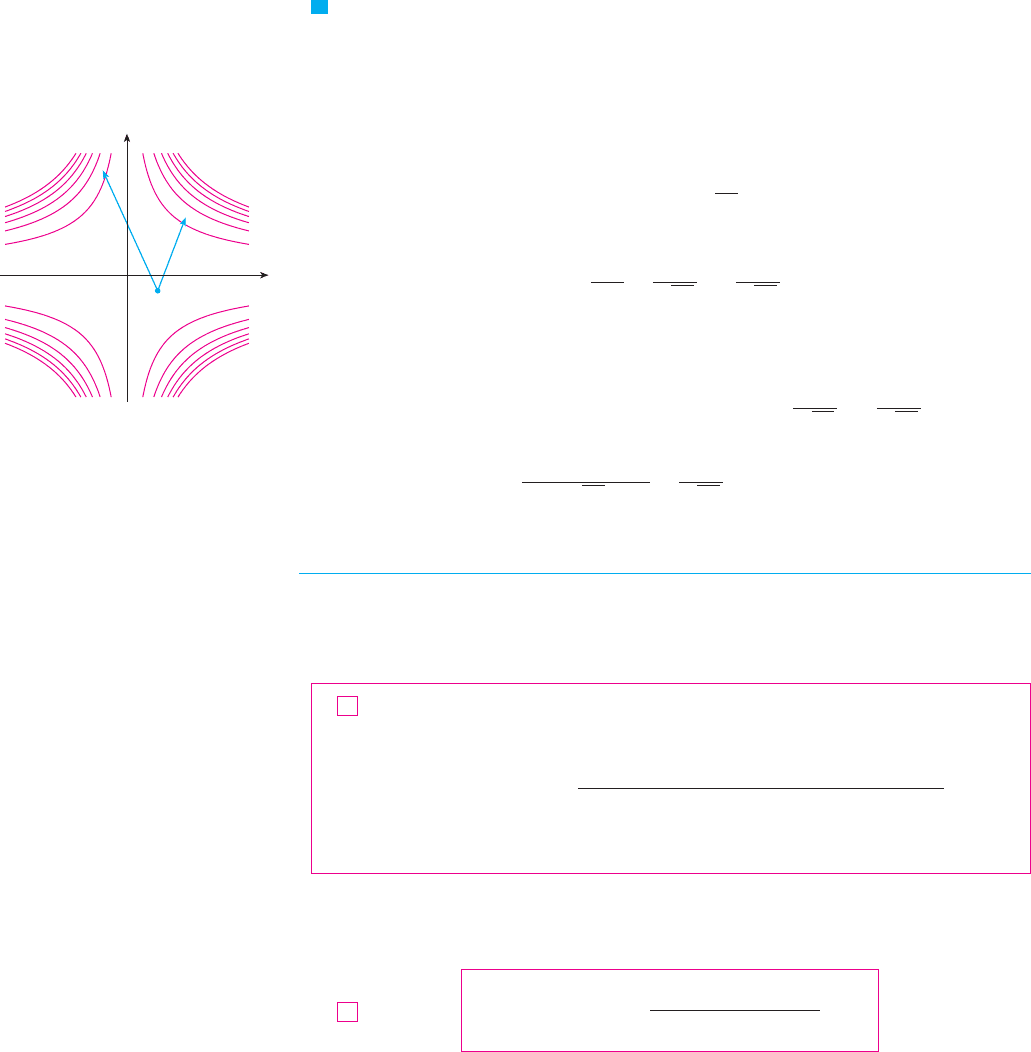
N The directional derivative in
Example 2 represents the rate of change of in
the direction of . This is the slope of the tan-
gent line to the curve of intersection of the
surface and the vertical
plane through in the direction of
shown in Figure 5.
u共1, 2, 0兲
z 苷 x
3
3xy 4y
2
u
z
D
u
f 共1, 2兲
FIGURE 5
(1,2,0)
π
6
z
x
y
0
u
EXAMPLE 4 Find the directional derivative of the function at the
point in the direction of the vector .
SOLUTION We first compute the gradient vector at :
Note that is not a unit vector, but since , the unit vector in the direction
of is
Therefore, by Equation 9, we have
M
FUNCTIONS OF THREE VARIABLES
For functions of three variables we can define directional derivatives in a similar manner.
Again can be interpreted as the rate of change of the function in the direction
of a unit vector .
DEFINITION The directional derivative of at in the direction of a
unit vector is
if this limit exists.
If we use vector notation, then we can write both definitions (2 and 10) of the direc-
tional derivative in the compact form
where if and if . This is reasonable because
the vector equation of the line through in the direction of the vector is given by
(Equation 13.5.1) and so represents the value of at a point on
this line.
ff 共x
0
⫹ hu兲x 苷 x
0
⫹ tu
ux
0
n 苷 3x
0
苷 具x
0
, y
0
, z
0
典n 苷 2x
0
苷 具x
0
, y
0
典
D
u
f 共x
0
兲 苷 lim
h
l
0
f 共x
0
⫹ hu兲 ⫺ f 共x
0
兲
h
11
D
u
f 共x
0
, y
0
, z
0
兲 苷 lim
h
l
0
f 共x
0
⫹ ha, y
0
⫹ hb, z
0
⫹ hc兲 ⫺ f 共x
0
, y
0
, z
0
兲
h
u 苷 具a, b, c 典
共x
0
, y
0
, z
0
兲f
10
u
D
u
f 共x, y, z兲
苷
⫺4 ⴢ 2 ⫹ 8 ⴢ 5
s
29
苷
32
s
29
D
u
f 共2, ⫺1兲 苷 ⵜf 共2, ⫺1兲 ⴢ u 苷 共⫺4 i ⫹ 8j兲 ⴢ
冉
2
s
29
i ⫹
5
s
29
j
冊
u 苷
v
ⱍ
v
ⱍ
苷
2
s
29
i ⫹
5
s
29
j
v
ⱍ
v
ⱍ
苷
s
29
v
ⵜf 共2, ⫺1兲 苷 ⫺4i ⫹ 8 j
ⵜf 共x, y兲 苷 2xy
3
i ⫹ 共3x
2
y
2
⫺ 4兲j
共2, ⫺1兲
v 苷 2 i ⫹ 5j共2, ⫺1兲
f 共x, y兲 苷 x
2
y
3
⫺ 4y
V
950
||||
CHAPTER 15 PARTIAL DERIVATIVES
N The gradient vector in Example 4
is shown in Figure 6 with initial point .
Also shown is the vector that gives the direc-
tion of the directional derivative. Both of these
vectors are superimposed on a contour plot of
the graph of .f
v
共2, ⫺1兲
ⵜf 共2, ⫺1兲
v
(2,_1)
±f(2,_1)
FIGURE 6
x
y

If is differentiable and , then the same method that was used to
prove Theorem 3 can be used to show that
For a function of three variables, the gradient vector, denoted by or grad , is
or, for short,
Then, just as with functions of two variables, Formula 12 for the directional derivative can
be rewritten as
EXAMPLE 5 If , (a) find the gradient of and (b) find the direc-
tional derivative of at in the direction of .
SOLUTION
(a) The gradient of is
(b) At we have . The unit vector in the direction of
is
Therefore Equation 14 gives
M
MAXIMIZING THE DIRECTIONAL DERIVATIVE
Suppose we have a function of two or three variables and we consider all possible direc-
tional derivatives of at a given point. These give the rates of change of in all possible
directions. We can then ask the questions: In which of these directions does change
fastest and what is the maximum rate of change? The answers are provided by the follow-
ing theorem.
f
ff
f
苷 3
冉
⫺
1
s
6
冊
苷 ⫺
冑
3
2
苷 3k ⴢ
冉
1
s
6
i ⫹
2
s
6
j ⫺
1
s
6
k
冊
D
u
f 共1, 3, 0兲 苷 ⵜf 共1, 3, 0兲 ⴢ u
u 苷
1
s
6
i ⫹
2
s
6
j ⫺
1
s
6
k
v 苷 i ⫹ 2 j ⫺ k
ⵜf 共1, 3, 0兲 苷 具0, 0, 3典共1, 3, 0兲
苷 具sin yz, xz cos yz, xy cos yz 典
ⵜf 共x, y, z兲 苷 具 f
x
共x, y, z兲, f
y
共x, y, z兲, f
z
共x, y, z兲典
f
v 苷 i ⫹ 2 j ⫺ k共1, 3, 0兲f
ff 共x, y, z兲 苷 x sin yz
V
D
u
f 共x, y, z兲 苷 ⵜf 共x, y, z兲 ⴢ u
14
ⵜf 苷 具 f
x
, f
y
, f
z
典 苷
⭸f
⭸x
i ⫹
⭸f
⭸y
j ⫹
⭸f
⭸z
k
13
ⵜf 共x, y, z兲 苷 具 f
x
共x, y, z兲, f
y
共x, y, z兲, f
z
共x, y, z兲典
fⵜff
D
u
f 共x, y, z兲 苷 f
x
共x, y, z兲 a ⫹ f
y
共x, y, z兲 b ⫹ f
z
共x, y, z兲 c
12
u 苷 具a, b, c 典f 共x, y, z兲
SECTION 15.6 DIRECTIONAL DERIVATIVES AND THE GRADIENT VECTOR
||||
951
