Teodorescu P.P. Mechanical Systems, Classical Models Volume I: Particle Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

represents a support of matter. If, after a series of mechanical phenomena (for instance,

after a succession of motions), material bodies maintain their properties of extent and

relative situation with respect to other material objects, one considers that they have the

same position. The physical space is formed by the totality of these positions, having

thus an absolute character. The properties of homogeneity and isotropy put into

evidence the fact that local properties of this space are independent of the position and

of the direction, respectively.

An observer who perceives mechanical phenomena of the material world from a

“laboratory” can put in evidence a “relation of order” for them; so appears the notion of

individual physical time. By synchronization of time scales of two observers one passes

from the individual physical time to the universal physical time; in this case, the

transmission of signals has an instantaneous character. Thus, in a classical model of

mechanics, the time has an absolute character, being the same for all observers who

study a certain mechanical phenomenon. Any material process has certain duration. We

say that an elementary material process, which has no duration (is of null duration), is

an event. If two events take place at the same time, then they are simultaneous; in the

contrary case, they are successive, one of them taking place before the other one. Thus,

the set of events is ordered, and the time, characterized by duration, simultaneity and

succession, is unidimensional. Admitting, in a classical model of mechanics, that time is

independent of matter, it results that – as in the case of the space – it has no structure;

hence, the time “flows” uniformly, being homogeneous. We mention also that the time

is infinite, continuous and irreversible.

The modelling of the space, as well as the modelling of the time, represents, in

classical mechanics, an approximation of the material reality; they are valid only in case

of small distances and small velocities with respect to the velocity of propagation of

light in vacuum.

1.1.4 Motion. Rest. Frames of reference

By mechanical motion we understand the change of position of a material body

with respect to another material body

B . In this case, at least a distance from a point

of the body

to a point of the body

varies in time; we say that the corresponding

points undergo certain displacements. This mechanical phenomenon has a relative

character; indeed, if the body

B moves with respect to the body

B , then the latter

one moves also with respect to the first one.

If we refer the motion (in what follows we leave out the adjective “mechanical”,

because we have to do only with such motions) of a body

B (we omit also the adjective

“material” in subsequent formulations) to another body

R, the latter one will be called

frame (system) of reference; in what follows, the frame of reference

R will be

considered to be rigid (the distances between any two points of it are constant in time),

being made up at least of three non-collinear points. If the distances of all the points of

the body

B to the frame R (to three non-collinear points of it) are constant in time,

then we say that this body is at rest with respect to this frame.

We cannot speak about absolute motion (only in the sense that matter is in

continuous motion) because an absolute frame of reference does not exist, but only

about relative motion; as well, we cannot speak about absolute rest, but only about

Newtonian model of mechanics

relative rest. Analogously, we cannot speak about absolute space or about absolute

time, but only about relative space (referring to a spatial frame), and about relative time

(referring to a temporal frame).

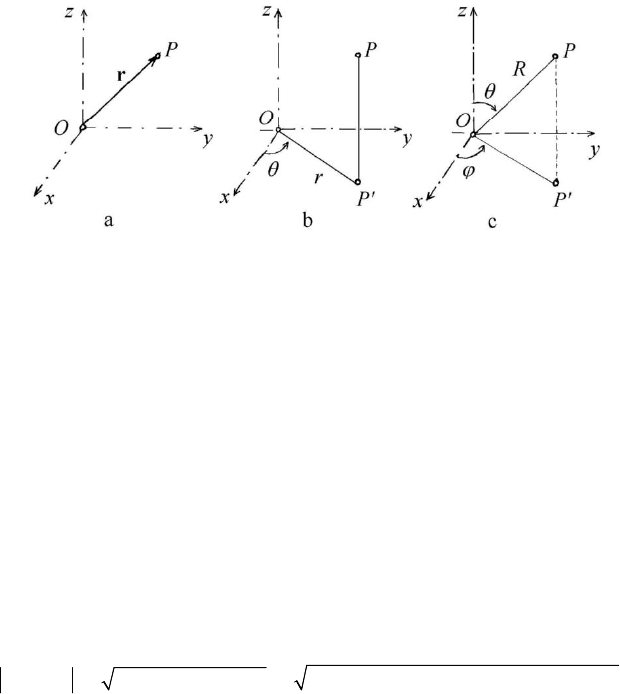
Figure 1.5. Orthogonal Cartesian (a), cylindrical (b) and spherical (c) co-ordinates.

The position of a point

P of a body will be given by the position vector r with

respect to the pole (origin)

O of a given frame of reference. We will consider only

frames the bases of which are positive, using various systems of co-ordinates. In

general, we use right-handed orthonormed frames (see Chap. 2, Subsec. 1.1.2); for

instance, in case of a system of orthogonal Cartesian co-ordinates, the position of the

point

P will be given by the co-ordinates

x ,

1, 2, 3i

, or by the abscissa x , the

ordinate

y and the applicate z (Fig.1.5,a), which are – at the same time – the

components of the position vector. In cylindrical co-ordinates, we use the polar radius

r , the polar angle θ and the applicate z (Fig.1.5,b), while in spherical co-ordinates

we introduce the polar radius

R , the colatitude θ and the azimuth (longitude) ϕ

(Fig.1.5,c) (the notations do not correspond in the two systems of co-ordinates, but we

like better to use well known notations); in general, we introduce arbitrary curvilinear

co-ordinates

q , = 1, 2, 3i .

The distance between two points

123

(, , )Px x x and

123

(, , )Qx x x will be given by

−=rr

−−=−+−+−

222

11 22 33

()()()( )( )

iiii

xyxy xy xy xy,

(1.1.15)

satisfying all the properties of the norm.

The time will be characterized by a variable

t , monotonous increasing, being

independent of any physical phenomenon and frame (observer). This variable can take

values on all the time axis

∈

−∞ ∞((,))t or we can admit the existence of an initial

moment

, from which starts the study of the considered phenomenon ∈∞

([,))tt ;

we can consider also that

∈

−∞

(,]tt or that

∈

[,]ttt. We can admit, without

loosing the generality, that

0t (we choose the initial moment as origin for the time

axis).

Long time, the scientists searched an absolute frame of reference in Universe,

admitting that – with respect to such a frame – the mathematical model of mechanics

takes its simplest form. So, in the geocentric frame of reference (Ptolemy’s frame) one

MECHANICAL SYSTEMS, CLASSICAL MODELS

admits that the origin is placed at the centre of mass of the Earth; usually, the equatorial

plane is taken as principal plane, one of the axes in this plane being straighten in the

direction of the vernal equinoctial point (at the intersection of the equatorial plane with

the ecliptic one, which contains the trajectory described by the Earth), while the third

axis is normal to this plane (hence, it is the rotation axis of the Earth). Later, one

considered the heliocentric frame of reference (Copernicus’ frame), in which the origin

is in the centre of mass of the Sun. In such a frame, the plane of the ellipse described by

the Earth, hence the ecliptic plane, is taken as principal plane (ecliptic heliocentric

frame of reference), or a plane parallel to the equatorial plane of the Earth is taken as

such a plane (equatorial heliocentric frame of reference), the third axis being normal to

the respective principal plane; in both cases, one of the axes contained in the principal

plane is along the direction of the vernal point (at the intersection of the ecliptic plane

with a plane parallel to the equatorial plane of the Earth, passing through the centre of

mass of the Sun), hence it is parallel to the axis considered in case of the geocentric

frame. Obviously, this last frame represents a progress with respect to the previous one,

leading to simpler properties of motion of planets. But the Sun is only one of more than

two hundred milliards of stars of our Galaxy, having – at this moment – a relatively

peripheral position in it; all these stars, including the Sun, move with respect to the

centre of mass of the Galaxy. We are thus led to a frame with the origin at this centre of

mass (a galactocentric frame of reference); the principal plane is the galactic median

plane, one of the axes contained in this plane being along its intersection with a plane

parallel to the equatorial plane of the Earth. In all these cases one uses the so-called

“fixed stars” (very far stars, the position of which are approximately fixed with respect

to observations which can be made on the Earth); knowing the positions of these stars

(their co-ordinates), one can use any of the frames mentioned above. A catalogue of

approximately 1500 such stars, called basic stars, has been elaborated. Theoretically,

only four stars are sufficient to identify a frame; practically, one considers a greater

number of stars, because – in any case – their positions vary in time, so that their

determination can be erroneous.

The laws of classical models of mechanics are sufficiently well verified in a

galactocentric frame of reference. But we observe that the motion of the heliocentric

frame with respect to the galactocentric one can be considered – with a good

approximation – to be a uniform and rectilinear translation, even for a relatively long

interval of time; one can thus use – in many cases – the heliocentric frame, obtaining

very good results, for instance in the study of motion of objects launched in the cosmic

space. For usual motions on the surface of the Earth, the geocentric frame of reference

leads also to very good results; the influence of the rotation and revolution motions of

the Earth can be introduced subsequently, every time it is necessary.

The frames of reference with respect to which the basic laws of mechanics can be

verified are called inertial frames of reference. If, in a classical model of mechanics, its

laws are verified in a certain frame of reference, then they are verified with respect to

any other frame in rectilinear and uniform motion with respect to the latter one; thus,

one obtains a class of inertial frames of reference. An “absolute space” in the sense of

Newton cannot be identified on the basis of a mechanical experiment.

The galactocentric frame of reference is an inertial one; as we have seen above, for

different cases of mechanical motion one can admit that the heliocentric frame of

reference or even the geocentric frame of reference are inertial frames. On this way, we

Newtonian model of mechanics

can construct also other frames of reference (considering a larger region of the universe,

at a greater scale), which are also inertial; but this is not necessary from the point of

view of classical models of mechanics.

1.1.5 Trajectory. Velocity. Acceleration

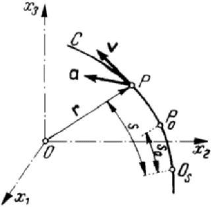
In what follows, let us consider the motion of a body with respect to a frame of

reference

R which, by convention, is admitted to be “fixed”. The motion of a point P

of the body with respect to this frame of reference is defined if, for any value of the time

Figure 1.6. Trajectory, velocity and acceleration of a particle P .

t in

E , we obtain its position in

E ; the point P describes thus, in its motion, a

trajectory

C (the geometric locus of positions occupied by point P ) (Fig.1.6), of

vector equation

rr()

(1.1.16)

or of parametric equations

()

xxt,

1, 2, 3i .

(1.1.16')

In cylindrical co-ordinates, these equations are written in the form

= ()rrt,

()tθθ,

()zzt

(1.1.16'')

and in spherical co-ordinates we have

= ()rrt,

()tθθ,

()tϕϕ ;

(1.1.16''')

In arbitrary curvilinear co-ordinates, they are given by

()

qqt,

1, 2, 3i .

(1.1.16

)

These equations define the law of motion. Eliminating the time

t between equations

(1.1.16'), one obtains the Cartesian equations (two equations) of the trajectory. The

knowledge of the trajectory in one of the forms mentioned above does not mean that we

know how the point

P is moving along this trajectory; to state accurately this motion

we must define the velocity and the acceleration of the point.

MECHANICAL SYSTEMS, CLASSICAL MODELS

The mechanical nature of the phenomenon of motion imposes certain conditions to

the vector function (1.1.16). So, it must be continuous (the trajectory is continuous, the

point cannot occupy simultaneously several positions in space) and bounded in modulus

for

∈

[,]ttt, where we have put in evidence the definition interval; if the condition of

boundedness is not fulfilled, then the trajectory has points at infinity. This function must

be also differentiable (obtaining thus the velocity and the acceleration), exception

making – eventually – a finite number of moments. If the vector function admits

everywhere derivatives of second order, then the motion is continuous, otherwise having

to do with a discontinuous motion (in fact, the denomination refers to the velocity, not

to the motion). In the last case, one can introduce regular distributions to characterize

the velocity, as well as regular distributions or singular (if it is necessary) distributions

to characterize the acceleration.

If the derivatives of first order of functions (1.1.16') are continuous at any moment

in the definition interval, then the trajectory is a rectifiable curve; we can introduce – in

this case – the curvilinear co-ordinate

s , measured from an arbitrary point

O as origin

(Fig.1.6). Taking the direction of motion as a positive one to measure arcs

s , we can

establish the correspondence

()sst,

(1.1.17)

which will be called the horary equation of motion; the graphic representation of this

function in a frame of reference

Ots will be the graph of the motion. From

=⋅= =rr r r

dd (d) d

()

()()()

==++

222

123

dddd d d

sxxx x x

(1.1.18)

we deduce

()

;()()d

sts s x xτττ=+

∫

 ,

(1.1.18')

s being the length of the trajectory till point

P , to which corresponds the initial

moment

t . In case of a finite number of discontinuity moments of the derivative of

first order of function (1.1.16), the curve is

piecewise rectifiable.

Let us introduce also the fixed frame of reference

′

R , rigidly connected with the

frame of reference

R ; the origin O

′

of the new frame will be specified by the position

vector

′

JJJG

r with respect to the first one. The point P will be thus given by the

new position vector

() ()tt

′

−rrr.

(1.1.19)

Differentiating successively with respect to time, vector

r will be eliminated, and one

obtains

′



rr,

′

 

rr,

′

 

rr…

(1.1.20)

Newtonian model of mechanics

Hence, one can affirm that

all derivatives of the position vector with respect to time are

invariant with respect to a change of a fixed frame of reference

. We mention the first

two invariants





(1.1.20')

which represent the

velocity and the acceleration of the point P , respectively, and play

an important rôle in mathematical modelling of classical mechanics.

1.1.6 Mass. Momentum

The mass is a

quantity of state (quantity which depends on the actual state of the

body but not on how one got to this state) which appears in all phenomena of motion,

being an

important property of matter; it does exist objectively and is independent of

the place where it is measured, as well as the electric charge in an electromagnetic field.

Newton introduced the concept of mass as a

measure of the amount of matter; this

concept has a statical character. But we observe that the mass is present in various

phenomena of motion too, and can be put in connection especially with the inertia and

the universal attraction of bodies.

Inertia is a general tendency of matter to conserve its state of rest or of rectilinear and

uniform motion; from this point of view, the mass represents a

measure of the inertia of

the body

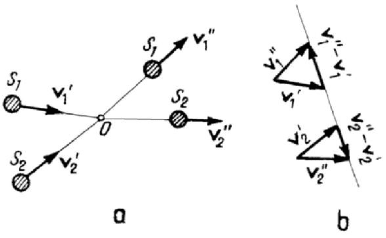
in motion. Let us consider a system formed by two homogeneous spheres

and

S , of negligible dimensions, which become in collision at point O (Fig.1.7,a);

they have the velocities

′

and

′

v before collision, and

′

and

′

after collision. One

observes that the variations of velocity

′

′′

−

vv and

′

′′

−

vv are vectors on the same

Figure 1.7. Collision of two small homogeneous spheres (a).

Variations of velocity (b).

support but of opposite sign (Fig.1.7,b). Ş. Ţiţeica has made such an experiment, using

two homogeneous small spheres fixed at the same fixed point by two inextensible

threads of the same length; one obtains thus two simple (mathematical) pendulums. The

isochronism of small oscillations (they take place in the same interval of time) ensures

the property of tautochronism (one arrives at the same position in the same time

interval, independently of the initial position), so that the spheres, starting from different

points, become in collision in a point corresponding to the vertical of the fixed point;

MECHANICAL SYSTEMS, CLASSICAL MODELS

the velocities before and after collision will be proportional to the respective

amplitudes, so that we can measure them. We may thus write

(

)

11 1222

′′ ′ ′′ ′

−

=− −vv vv,

(1.1.21)

where

μ is a positive scalar; repeating the experiment with the same spheres but other

velocities

′

and

′

, one observes that this scalar is constant, depending only on the

chosen spheres (it is a characteristic of their interaction, this fact being put in evidence

by the two indices). Let us consider now three homogeneous spheres

S ,

S and

S , of

negligible dimensions; repeating the experiment with these spheres taken two by two,

we find a relation of the form

12 13 32

μμμ.

(1.1.21')

Supposing now that

12 12 1 2

(, )XXμμ , where

X and

X are quantities which

characterize the spheres

S and

S , respectively, it follows from (1.1.21') that =

1μ

if the spheres

S and

S are identical; if the spheres

S and

S are identical and we

take into account the previous result, then we can write also

13 31

1/μμ. Relation

(1.1.21') becomes

(

)

()

32 32 3 2

31 31 3 1

μμ

and is valid for any sphere; there results that

μ is the ratio of two scalars, each one

depending only on quantities characterizing the spheres

and

, respectively. We

can thus write

, >

,0mm .

(1.1.22)

In this case, relation (1.1.21) shows that, for the same scalar

m and for the same

variation of velocity

′′ ′

−

vv (in modulus), if the scalar

m is greater, then the

variation

′′ ′

−

vv is smaller; the velocity of the sphere

S is subject to a smaller

variation, its inertia being greater. The inertia of the sphere

S increases thus at the

same time as the scalar

m ; the latter one can be considered as a measure of the inertia

of the respective sphere (analogously,

m measures the inertia of the sphere

S ). So,

one can attach to a homogeneous sphere

S of negligible dimensions an inertial mass

> 0

In what concerns the universal attraction of bodies, let us consider their falling on the

surface of the Earth (the action of the terrestrial gravitational field). We can measure the

attraction, by the Earth, of two homogeneous spheres

S and

S , of negligible

dimensions (their weight), using a dynamometer (hence, measuring some lengths); the

Newtonian model of mechanics

two gravity forces

and

, which are thus put in evidence, have the same direction,

so that we can write

1122

ν , >

0ν .

(1.1.23)

Considering three homogeneous spheres

S ,

S and

S , of negligible dimensions, we

can establish a relation of the form

12 13 32

ννν;

(1.1.23')

by a reasoning similar to that above, we attach to the sphere

S a gravitational mass

> 0

m . This scalar does not depend on the position on the surface of the Earth in

which the experiment takes place.

Very fine experiments made by L. Eötvös in 1890 and taken again by Zeeman in

1917, led to

proportionality between the inertial mass and the gravitational one (a body

is as much inertial as it is heavy). Taking conveniently the units, we may have a

proportionality coefficient equal to unity, hence the relation

=>0

mm m ,

(1.1.24)

which emphasizes the equality between the inertial mass and the gravitational one; in

what follows, it will no more be necessary to characterize the respective property of the

mass using the adjectives “inertial ” and “gravitational”. This equality has a quantitative

(numerical) aspect in classical mechanics; in relativistic mechanics (general relativity),

its qualitative aspects will also appear.

We mention an experiment made by W. Pohl, which puts in evidence the aspects of

inertial and gravitational mass, respectively. A homogeneous sphere is linked in two

Figure 1.8. W. Pohl’s experiment on inertial and gravitational mass.

diametral opposite points

A and 'A by two identical threads AB and ''AB ; the end B

is connected at a fixed point, while at the end

'B acts a force

(Fig.1.8). If the force

F acts suddenly (from the very beginning with its entire intensity), then the thread

''AB breaks (because of the inertial aspect of the mass), while if this force has a static

action (the intensity of the force growth in a short but finite time), then the thread

breaks (the influence of the force

F is added to the weight of the sphere, and the

gravitational aspect of the mass is emphasized).

The Newtonian character of mass, i.e. to be a

measure of the quantity of matter of a

body, may be experimentally verified; indeed, the mass of several bodies is equal to the

MECHANICAL SYSTEMS, CLASSICAL MODELS

sum of the masses of the bodies, as it can be seen if we put in evidence the gravitational

aspect of mass (the weights of bodies, measured with the aid of a dynamometer, in a

certain place of the Earth, can be added). This is a

property of additivity.

Thus, in a mathematical modelling, we associate to each body

B a quantity of state

()m B called mass, having the following properties:

i) the mass of the body is a positive scalar (

>()0m B );

ii) for each division (disjoint parts)

B ,

1,2,...,in, of the body we can write

(the property of additivity)

()

∑

()

mmBB.

(1.1.25)

In a classical model of mechanics we admit also that:

iii)

the mass of the body remains constant during the motion =(0)m ; the

property is modified in case of a body of variable mass.

Space, time and mass are independent one of each other in a classical model of

mechanics.

Newton has introduced the notion of

momentum (which he called quantity of motion,

denomination of a statical character; it will not be used in what follows)

mv ,

representing the product of the mass by the velocity of a point of the body

B, as a

measure of the mechanical motion; we observe that, in a motion of translation, the

property of additivity takes place for any division

B of the body. Taking into account

(1.1.22) in relation (1.1.21), one obtains

11 22 11 22

mm mm

′′ ′′′′

=+vv vv;

(1.1.26)

that means that the momentum of the two homogeneous spheres of negligible

dimensions remains constant during the phenomenon of collision. It is thus justified to

consider the momentum to be a characteristic of mechanical motion, a

measure of it.

One can state also that relation (1.1.26) puts in evidence the capacity of a mechanical

motion to be transformed into another mechanical motion.

1.1.7 Mathematical modelling of discontinuous phenomena. Distributions. Stieltjes

integral

To study discontinuous phenomena together with continuous ones it is necessary to

introduce the notion of distribution and Stieltjes integral in distributions; in fact, this

mathematical modelling is the only one which allows a correct representation of the

respective phenomenon. In this order of ideas, we will give some basic results and

formulae to be used in what follows.

We call

functional a mapping of a vector space

(with respect to

) into

. If

is the corpus of real numbers

R , then we say that we have to do with a real functional.

We call

distribution a continuous linear functional defined on a topological vector space

(fundamental space).

By definition, the fundamental space

K is constituted of the functions of real

variables

()xϕ ( ≡

( , ,..., )

xxx x represents a point in

R ), indefinite differentiable

(of class

∞

) and vanishing together with all their derivatives in the exterior of certain

Newtonian model of mechanics

bounded domains; these domains, together with their boundaries, determine the

supports of these functions, called

fundamental functions (by support of a function

()xϕ we mean the smallest closed set which contains the set of points x for which

≠() 0xϕ ). By an extension of the space

we reach another class of functions, which

determine the fundamental space

S . The functions belonging to this class have also the

property to be indefinite differentiable; for

→∞x these functions tend to zero

together with their derivatives of any order, more rapidly that any power of

1/ x . We

introduce also the space

K , which includes the functions with compact support,

having continuous derivatives up to and including the

mth order (of class

C ). The

distributions

defined on spaces

and

K are called of infinite order, temperate

and

of finite order ≤pm, respectively.

Let

()

x be a function defined on the real axis R ; we say that this function is

absolutely integrable in a closed interval [,]ab of R , if the integral

()d

fx x

∞

∫

(1.1.27)

exists.

If the function

()

x is absolutely integrable in any finite interval of R , then we say

that

()

x is a locally integrable function. We mention that an absolutely integrable

function is also

integrable, i.e. the integral

()d

∫

(1.1.27')

exists.

Locally integrable functions generate an important class of distributions; we assume

thus that to any fundamental function

()xKϕ ∈ there corresponds a real number

()

, ()()d ()()d

fx x x fx x xϕϕ ϕ==

∫∫

(1.1.28)

where

()

x is a locally integrable function and [,]ab is the support of ()xϕ . It is easy

to see that the functional thus defined is linear and continuous. The functional defined

on space

K by means of the locally integrable function ()

x represents a distribution

on this space, which will be denoted also by

()

x , like the generating function. Such

distributions are called

regular distributions (distributions of function type).

Analogously, one can define

temperate regular distributions on space S .

The distributions, which are not of function type, are called

singular distributions. If

to any function

∈()xKϕ we attach its value in the origin (the value (0)ϕ ), then we

see that the respective functional is linear and continuous, hence it is a distribution

which is not regular; this is

the Dirac distribution, which will be denoted by the symbol

()xδ . Symbolically, we write